Python蓝桥杯训练:基本数据结构 [二叉树] 上
Python蓝桥杯训练:基本数据结构 [二叉树] 上
文章目录
- Python蓝桥杯训练:基本数据结构 [二叉树] 上
- 一、前言
- 二、有关二叉树理论基础
- 1、二叉树的基本定义
- 2、二叉树的常见类型
- 3、二叉树的遍历方式
- 三、有关二叉树的层序遍历的题目
- 1、[二叉树的层序遍历](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
- 2、[N叉树的层序遍历](https://leetcode.cn/problems/n-ary-tree-level-order-traversal/)
- 3、填充每个节点的下一个右侧节点指针
一、前言
目前蓝桥杯训练刷题刷到了二叉树,中间的栈和队列我没有更新,时间有点不太够,但是我又觉得如果刷题不写笔记的话感觉等于没刷,所以我还是将我刷题的过程以笔记的形式总结出来,内容可能没有之前几次的丰富但是我还是会将重要的内容总结出来,理论部分会有所减少,我会更加专注 于总结刷题过程中的思考。
二、有关二叉树理论基础
二叉树是一种树状数据结构,它的每个节点最多只有两个子节点。其中一个被称为左子节点,另一个被称为右子节点。以下是有关二叉树的理论基础的详细总结:
1、二叉树的基本定义
- 节点(Node):二叉树的基本单位,它包含一个值(Value)和两个指针(Pointer),分别指向左子节点和右子节点(如果没有子节点,则指向 null 或空)。
- 根节点(Root):二叉树中的第一个节点,它没有父节点,是整棵树的起点。
- 叶节点(Leaf):没有子节点的节点称为叶节点。
- 内部节点(Internal Node):除了叶节点以外的节点都称为内部节点。
- 高度(Height):二叉树的高度是从根节点到最深叶节点的最长路径的长度。空树的高度为0,只有一个节点的二叉树的高度为1。
- 深度(Depth):节点的深度是从根节点到该节点的唯一路径的长度。根节点的深度为0。
- 路径(Path):是指从一个节点到另一个节点经过的所有节点的序列。
- 子树(Subtree):是指由一个节点及其所有后代节点组成的二叉树。
2、二叉树的常见类型
- 普通二叉树(Binary Tree):每个节点最多只有两个子节点。
- 完全二叉树(Complete Binary Tree):除了最后一层,每一层的节点数都是满的,并且最后一层的节点都尽可能地靠左。
- 满二叉树(Full Binary Tree):每个节点都有 0 或 2 个子节点,没有只有一个子节点的节点。
- 二叉搜索树(Binary Search Tree):每个节点的左子树中的所有节点的值都小于该节点的值,右子树中的所有节点的值都大于该节点的值。
- 平衡二叉树(Balanced Binary Tree):左右子树的高度差不超过 1 的二叉树。
3、二叉树的遍历方式
二叉树的深度优先遍历方式有三种:前序遍历、中序遍历和后序遍历,广度优先遍历有层序遍历。这些遍历方式都是基于递归的,它们都可以使用递归或迭代法来实现。
-
深度优先遍历
-
前序遍历:先访问根节点,再递归地访问左子树和右子树。
class Node:def __init__(self, value):self.left = Noneself.right = Noneself.value = valuedef preorder_traversal(node):if node is None:returnprint(node.value)preorder_traversal(node.left)preorder_traversal(node.right)root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)print("前序遍历结果:") preorder_traversal(root)前序遍历结果: 1 2 4 5 3 -
中序遍历:先递归地访问左子树,再访问根节点,最后递归地访问右子树。
class Node:def __init__(self, value):self.left = Noneself.right = Noneself.value = valuedef inorder_traversal(node):if node is None:returninorder_traversal(node.left)print(node.value)inorder_traversal(node.right)root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)print("中序遍历结果:") inorder_traversal(root)中序遍历结果: 4 2 5 1 3 -
后序遍历:先递归地访问左子树和右子树,最后访问根节点。
class Node:def __init__(self, value):self.left = Noneself.right = Noneself.value = valuedef postorder_traversal(node):if node is None:returnpostorder_traversal(node.left)postorder_traversal(node.right)print(node.value)root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)print("后序遍历结果:") postorder_traversal(root)后序遍历结果: 4 5 2 3 1
-
-
广度优先遍历
也称作层序遍历,是按照层次顺序从上往下、从左往右遍历树的节点。广度优先遍历需要借助队列来实现,每次从队列中取出一个节点,访问它的左右子节点,将子节点依次加入队列中,直到队列为空。
from collections import dequeclass Node:def __init__(self, value):self.left = Noneself.right = Noneself.value = valuedef breadth_first_traversal(node):if node is None:returnqueue = deque()queue.append(node)while queue:current_node = queue.popleft()print(current_node.value)if current_node.left:queue.append(current_node.left)if current_node.right:queue.append(current_node.right)root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)print("广度优先遍历结果:") breadth_first_traversal(root)广度优先遍历结果: 1 2 3 4 5
三、有关二叉树的层序遍历的题目
二叉树的层序遍历相比于其深度优先遍历会简单很多,基本记住一个模板很多题目就可以直接套用。
1、二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
-
树中节点数目在范围 [0, 2000] 内
-
-1000 <= Node.val <= 1000
这道题就是考察我们对二叉树层序遍历的掌握情况,在上面的二叉树理论基础中的广度优先遍历中我们已经实现了这个过程,并且使用的迭代方法,下面我来说一下递归的方法如何实现。
实现思路跟迭代法一样就是代码更加简洁,具体思路我写在了代码注释里面。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution():def levelOrder(self, root: TreeNode) -> List[List[int]]:result = [] # 定义一个列表,用于保存最终结果def traverse(node, level):if not node: # 如果当前节点为空,直接返回returnif level == len(result): # 如果 result 中不存在当前层的列表,创建一个新的列表result.append([])result[level].append(node.val) # 将当前节点的值加入当前层的列表中traverse(node.left, level + 1) # 6递归遍历当前节点的左子树traverse(node.right, level + 1) # 7. 递归遍历当前节点的右子树traverse(root, 0) # 开始遍历二叉树return result # 返回最终结果
2、N叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:

输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]
示例 2:

输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
提示:
- 树的高度不会超过
1000 - 树的节点总数在
[0, 10^4]之间
这道题目也是套模板,只不过在左孩子和右孩子的基础上多了一个孩子。
"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""
# 迭代法
class Solution:def levelOrder(self, root: 'Node') -> List[List[int]]:if not root:return []res = []queue = [root]while queue:level = []size = len(queue)for i in range(size):node = queue.pop(0)level.append(node.val)for child in node.children:queue.append(child)res.append(level)return res递归法实现就是从根节点开始,递归遍历每一层的节点,并将它们添加到对应层的列表中。
class Solution:def levelOrder(self, root: 'Node') -> List[List[int]]:if not root: # 如果根节点为空,则直接返回空列表return []res = [] # 存储结果的列表def traverse(node, level):# 如果当前层数等于列表长度,则向列表中添加一个新列表if len(res) == level:res.append([])# 将当前节点的值加入到对应层的列表中res[level].append(node.val)# 递归遍历当前节点的所有子节点,并将它们的层数加一,作为递归函数的参数进行递归for child in node.children:traverse(child, level+1)# 从根节点开始递归遍历traverse(root, 0)return res # 返回结果列表
3、填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = []
输出:[]
提示:
- 树中节点的数量在
[0, 212 - 1]范围内 -1000 <= node.val <= 1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
这道题目的要求就是给定一棵二叉树,将每个节点的右子节点指向其在右边的下一个节点,如果右边没有节点,则将其指向None。要求使用常数级额外空间,也就是说不可以使用队列等数据结构。
题目要求在不使用队列等数据结构的情况下,将每个节点的右子节点指向其在右边的下一个节点。
我们可以从根节点开始,对于每一层节点,依次更新它们的右子节点,直到该层节点的最后一个节点。然后再进入下一层节点进行同样的操作。
具体来说我们指定一个指针 cur,表示当前层节点的最左边的节点,初始时 cur 指向根节点。在每一层的循环中,我们从左到右遍历该层的所有节点,对于每个节点,先将其左子节点的 next 指针指向其右子节点,再将其右子节点的 next 指针指向其 next 指针所指向节点的左子节点(如果该节点的 next 指针所指向节点不存在,则将其右子节点的 next 指针指向 None)。然后将该节点移动到下一个节点,直到该层的所有节点都被更新为止。最后将 cur 指针移动到下一层的最左边的节点,并重复上述操作,直到遍历完所有层为止。
"""
# Definition for a Node.
class Node:def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):self.val = valself.left = leftself.right = rightself.next = next
"""class Solution:def connect(self, root: 'Node') -> 'Node':if not root:return Nonecur = rootwhile cur.left:node = curwhile node:node.left.next = node.rightif node.next:node.right.next = node.next.leftnode = node.nextcur = cur.leftreturn root
时间复杂度:O(n)O(n)O(n),其中 nnn 是二叉树中的节点个数。
空间复杂度:O(1)O(1)O(1)。除了存储答案所需的空间外,我们只需要维护常数个变量,因此空间复杂度是 O(1)O(1)O(1)。
相关文章:

Python蓝桥杯训练:基本数据结构 [二叉树] 上
Python蓝桥杯训练:基本数据结构 [二叉树] 上 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 上一、前言二、有关二叉树理论基础1、二叉树的基本定义2、二叉树的常见类型3、二叉树的遍历方式三、有关二叉树的层序遍历的题目1、[二叉树的层序遍历](http…...
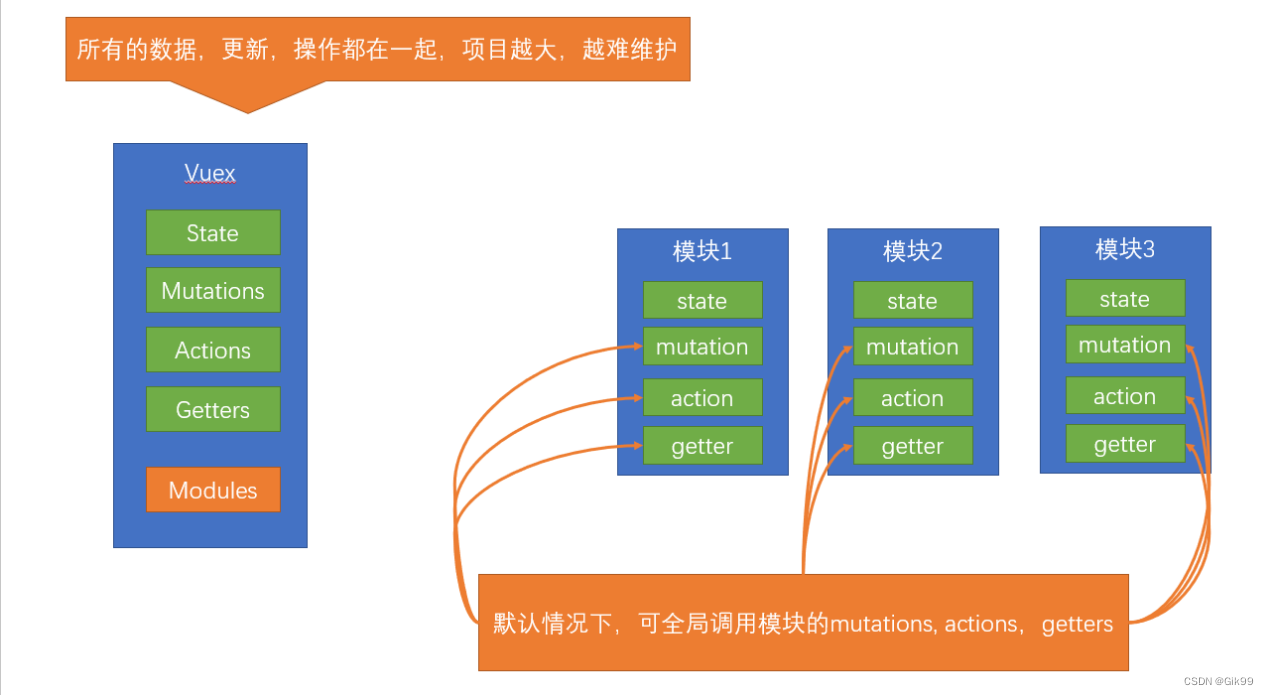
vuex基础之初始化功能、state、mutations、getters、模块化module的使用
vuex基础之初始化功能、state、mutations、getters、模块化module的使用一、Vuex的介绍二、初始化功能三、state3.1 定义state3.2 获取state3.2.1 原始形式获取3.2.2 辅助函数获取(mapState)四、mutations4.1 定义mutations4.2 调用mutations4.2.1 原始形式调用($store)4.2.2 辅…...

WebSphere中间件漏洞总结
WebSphere中间件漏洞总结 一、WebSphere简介 WebSphere为SOA(面向服务架构)环境提供软件,以实现动态的、互联的业务流程,为所有业务情形提供高度有效的应用程序基础架构。WebSphere是IBM的应用程序和集成软件平台,包含所有必要的中间件基础架构(包括服务器、服务和工具)…...

Unity之ASE实现影魔灵魂收集特效
前言 我们今天来实现一下Dota中的影魔死亡后,灵魂收集的特效。效果如下: 实现原理 1.先添加一张FlowMap图,这张图的UV是根据默认UV图,用PS按照我们希望的扭曲方向修改的如下图所示: 2.通过FlowMap图,我…...

半入耳式耳机运动会不会掉、佩戴超稳固的运动耳机推荐
现在越来越多的人开始意识到运动的重要性,用运动给身体增加一道“防护墙”是最好的生活方式了,不过,日复一日做着几乎相同的动作,难免索然无味,所以很多人都会选择在运动时戴上耳机听歌解闷,这时候也有不少…...
使用Tensorflow完成一个简单的手写数字识别
Tensorflow中文手册 介绍TensorFlow_w3cschool 模型结构图: 首先明确模型的输入及输出(先不考虑batch) 输入:一张手写数字图(28x28x1像素矩阵) 1是通道数 输出:预测的数字(1x10的one…...

OpenGL三种向着色器传递数据的方法 attributes,uniform,texture以及中间产物
(1)属性,使在顶点着色器中使用的变量,用于描述顶点的属性,如位置、颜色、法向量等,attributes通常用于描述每个顶点的属性,因此在顶点缓冲对象中存储,渲染的时候,openGL会…...

详解package.json和package-lock
详解package.json和package-lockpackage.json和package-lock.json作用首先要明确一点,package.json不会自动生成,需要我们使用 npm init 创建。package-lock.json是自动生成的,我们使用 npm install 安装包后就会自动生成。在我们执行 npm in…...

02-CSS
一、emmet语法1、简介Emmet语法的前身是Zen coding,它使用缩写,来提高html/css的编写速度, Vscode内部已经集成该语法。快速生成HTML结构语法快速生成CSS样式语法2、快速生成HTML结构语法生成标签 直接输入标签名 按tab键即可 比如 div 然后tab 键, 就可以生成 <…...

JavaScript 中的类型转换机制以及==和===的区别
目录一、概述二、显示转换Number()parseInt()String()Boolean()三、隐式转换自动转换成字符串自动转换成数值四、 和 区别1、等于操作符2、全等操作符3、区别小结一、概述 我们知道,JS中有六种简单数据类型:undefined、null、boolean、string、number、…...
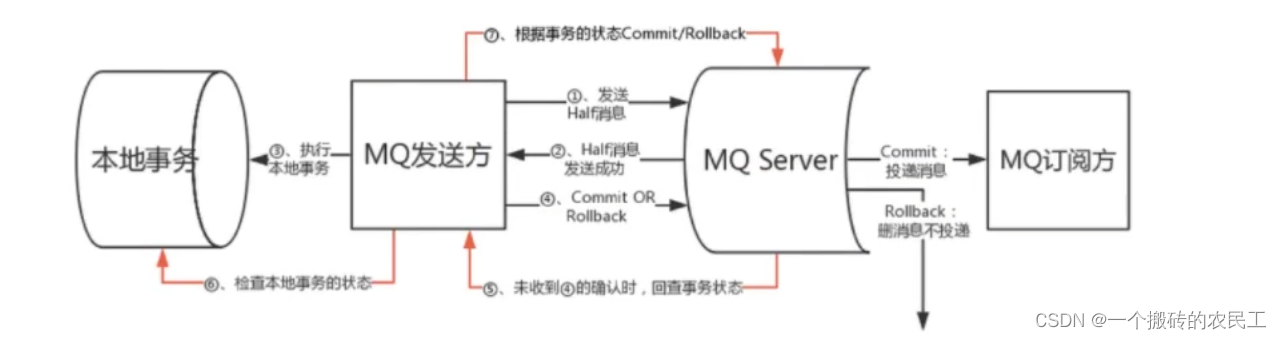
RocketMQ基础篇(一)
目录一、发送消息类型1、同步消息2、异步消息3、单向消息4、顺序消费5、延迟消费二、消费模式1、集群模式2、广播模式3、消费模式扩展4、如何配置三、其他用法1、事务消息2、过滤消息1)Tag过滤2)SQL方式过滤源码放到了GitHub仓库上,地址 http…...

Android前沿技术—gradle中的build script详解
build.gradle是gradle中非常重要的一个文件,因为它描述了gradle中可以运行的任务,今天本文将会带大家体验一下如何创建一个build.gradle文件和如何编写其中的内容。 project和task gradle是一个构建工具,所谓构建工具就是通过既定的各种规则…...

深入浅出PaddlePaddle函数——paddle.zeros_like
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出PaddlePaddle函数——paddle.Tensor 深入浅出PaddlePaddle函数——paddle.ones 深入浅出PaddlePaddle函数——paddle.zeros 深入浅出PaddlePaddle函数——paddle.full 深入浅出Padd…...

物料-零部件分类属性
离散制造业的研发、生产跟产品零部件紧密联系在一起,从企业业务流程来说零部件涉及研发、采购、仓储、生产、质量、售后和配件等多个部门,为了更好地管理零部件,下面我们一起来看看零部件概念及分类。 1、按行业属性分类 (1&…...

TypeError: cannot pickle ‘module‘ object
创建python对象时报错: TypeError: cannot pickle module object 原因: 很大可能是类成员错误的使用了第三方包(别名)等,具体排查方法可参考: import redisimport pickle from pprint import pformat as …...
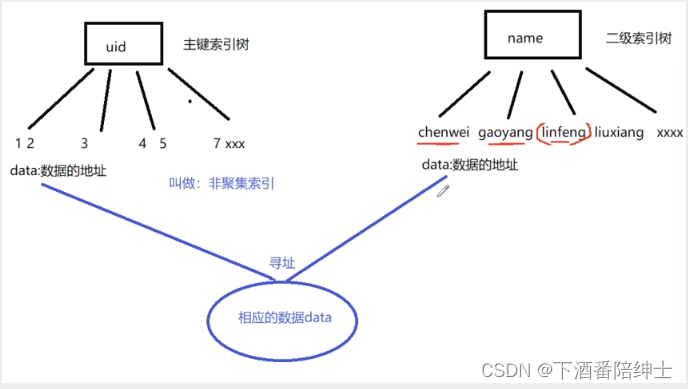
[MySQL索引]3.索引的底层原理(二)
索引的底层原理(二)InnoDB的主键和二级/辅助索引树(涉及回表)MyISAM存储引擎的主键和二级索引树InnoDB的主键和二级/辅助索引树(涉及回表) 看下面这张student数据库表: 场景一:uid…...

JavaScript混淆——逆向思维的艺术
在本文中我们将介绍三种常见的JavaScript混淆技术。 1.混合名称 通过将函数名称和变量名混合使用,我们可以使代码更难读。下面是一个使用名称混合的JavaScript函数。 function c(a){var b[2,4,8,a],db[0]b[1]b[2]b[3],ed""a;return e}混合名称技术通过…...
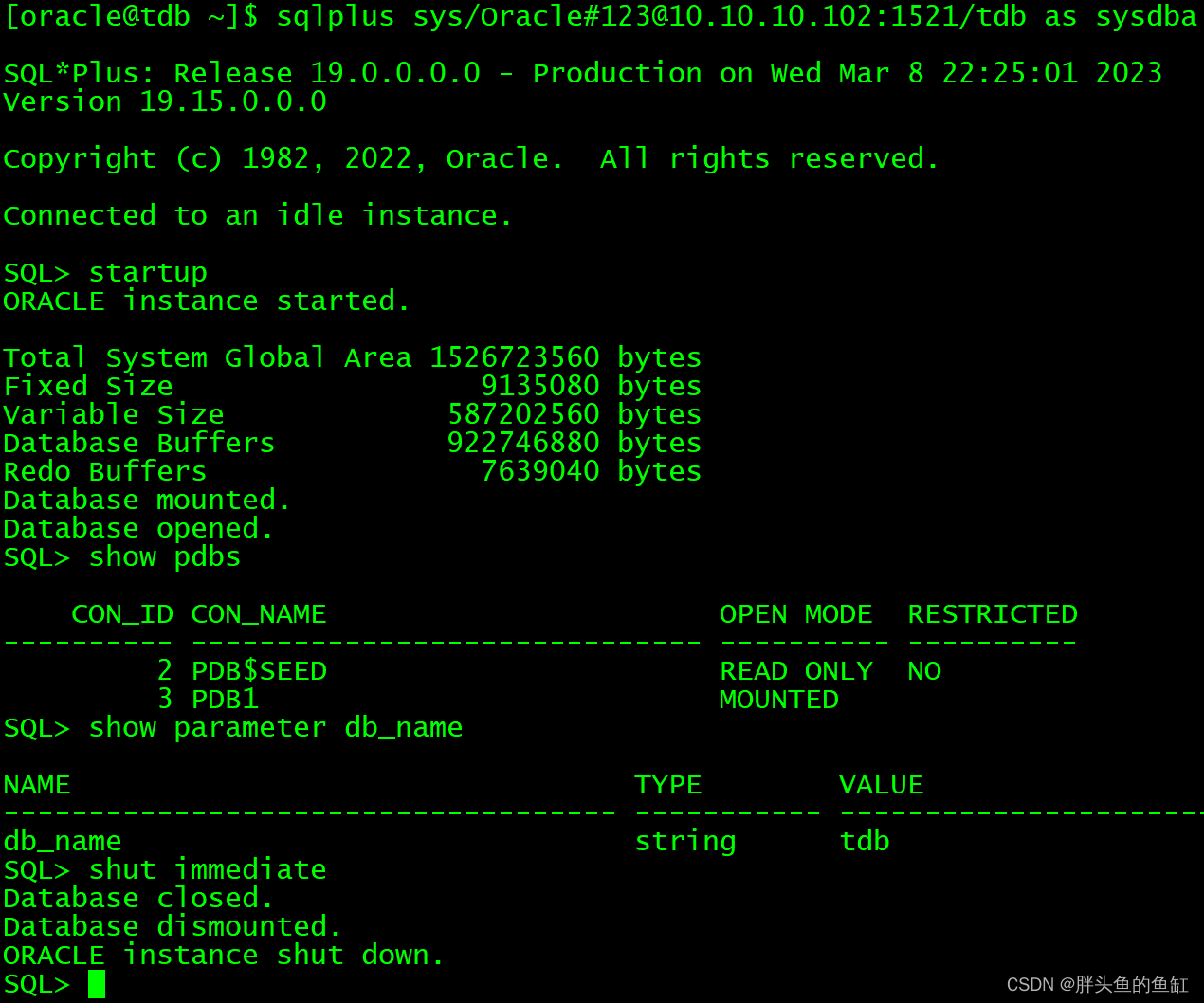
数据库管理-第六十期 监听(20230309)
数据库管理 2023-03-09第六十期期 监听1 无法访问2 监听配置3 问题复现与解决4 静态监听5 记不住配置咋整总结第六十期期 监听 不知不觉又来到了一个整10期数,我承认上一期有很大的划水的。。。嫌疑吧,本期内容是从帮群友解决ADG前置配置时候的一个问题…...

概率论与数理统计相关知识
本博客为《概率论与数理统计--茆诗松(第二版)》阅读笔记,目的是查漏补缺前置知识数学符号连乘符号:;总和符号:;“任意”符号:∀;“存在”符号&…...

SOC计算方法:卡尔曼滤波算法
卡尔曼滤波算法是一种经典的状态估计算法,它广泛应用于控制领域和信号处理领域。在电动汽车领域中,卡尔曼滤波算法也被广泛应用于电池管理系统中的电池状态估计。其中,电池的状态包括电池的剩余容量(SOC)、内阻、温度等…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
