AtCoder292 E 思维
题意:
给定一副n(n≤3000)n(n\leq 3000)n(n≤3000)个顶点,mmm条有向边的图,可以在图中添加有向边,求添加的最少边数,使得这副图满足:如果顶点aaa到顶点bbb有边,顶点bbb到ccc右有边,那么顶点aaa到顶点ccc也有边
Solution:
考虑一条单向链,按指向的方向按顺序是A,B,C,D,...A,B,C,D,...A,B,C,D,...
显然,A→B,B→CA\rightarrow B,B\rightarrow CA→B,B→C需要添加一条边A→CA\rightarrow CA→C,此时A→C,C→DA\rightarrow C,C\rightarrow DA→C,C→D需要添加A→DA\rightarrow DA→D。更一般的情况是,在从AAA出发能到达的顶点里,只有与AAA距离为1的不需要添加边,只需要和其他点建边即可,并查集不适合有向图,O(n)O(n)O(n)的搜索可以满足要求,每个顶点搜索一次,总复杂度O(n2)O(n^2)O(n2)
#include<iostream>
#include<vector>
#include<cstdlib>
#include<numeric>
#include<unistd.h>
#include<queue>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<set>
#include<map>
#include<stack>
#include<utility>
#include<cctype>
#include<cassert>
#include<thread>
#include<bitset>
using namespace std;using ll=long long;
const int N=2e5+5,inf=0x3fffffff;
const long long INF=0x3fffffffffffffff,mod=998244353;struct way {int to,next;
}edge[N<<1];
int cnt,head[N];void add(int u,int v) {edge[++cnt].to=v;edge[cnt].next=head[u];head[u]=cnt;
}int n,m,dis[N],vis[N];int main() {#ifdef stdjudgefreopen("in.txt","r",stdin);auto TimeFlagFirst=clock();#endifstd::ios::sync_with_stdio(false);std::cin.tie(nullptr);cin>>n>>m;for(int i=1;i<=m;i++) {int u,v;cin>>u>>v;add(u,v);}int tot=0;queue<int>q;for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) vis[j]=false;while(!q.empty()) q.pop();q.push(i);while(!q.empty()) {int u=q.front(); q.pop();vis[u]=true;for(int j=head[u];j;j=edge[j].next) {int v=edge[j].to;if(vis[v]) continue;q.push(v);}}for(int j=1;j<=n;j++) {if(i!=j&&vis[j]) tot++;}for(int j=head[i];j;j=edge[j].next) tot--;}cout<<tot<<endl;#ifdef stdjudgefreopen("CON","r",stdin);std::cout<<std::endl<<"耗时:"<<std::clock()-TimeFlagFirst<<"ms"<<std::endl;std::cout<<std::flush;system("pause");#endifreturn 0;
}
相关文章:

AtCoder292 E 思维
题意: 给定一副n(n≤3000)n(n\leq 3000)n(n≤3000)个顶点,mmm条有向边的图,可以在图中添加有向边,求添加的最少边数,使得这副图满足:如果顶点aaa到顶点bbb有边,顶点bbb到ccc右有边,…...

20230309英语学习
What Is Sleep Talking? We Look at the Science 为什么人睡觉会说梦话?来看看科学咋说 Nearly everyone has a story about people talking in their sleep.Though it tends to be more common in children, it can happen at any age:A 2010 study in the jour…...
CAD转换PDF格式怎么弄?教你几种方法轻松搞定!
CAD是从事与艺术创作相关等行业的打工人们必需的工作软件,可以用来完成建筑设计图、设计图纸等。在日常的工作中,一些伙伴经常需要传输图纸给合作方来完成探讨。但是CAD图纸需要使用专业软件才能打开,这就给文件传送带来了一定的困难。而且传…...

AtCoder 259E LCM
题意: 以唯一分解形式给出nnn个数: aipi,1ei,1pi,2ei,2...pi,tei,ta_{i}p_{i,1}^{e_{i,1}}p_{i,2}^{e_{i,2}}...p_{i,t}^{e_{i,t}} aipi,1ei,1pi,2ei,2...pi,tei,t 现在可以将某个数改为111,求所有改法中,有多少个…...

MQTT协议-取消订阅和取消订阅确认
MQTT协议-取消订阅和取消订阅确认 客户端向服务器取消订阅 取消订阅的前提是客户端已经通过CONNECT报文连接上服务器,并且订阅了一个主题 UNSUBSCRIBE—取消订阅 取消订阅的报文同样是由固定报头可变报头有效载荷组成 固定报头由两个字节组成,第一个…...
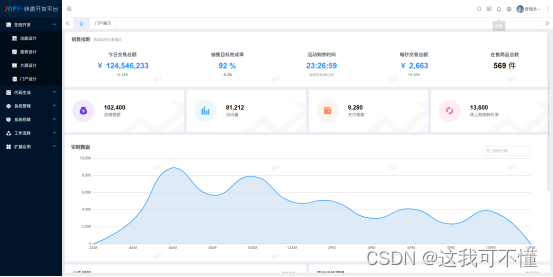
90后小伙,用低代码“整顿”旅游业,年入2000万,他是怎么做到的?
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

C51---PWM 脉冲宽度调制
1.PWM:脉冲宽度调制,它是通过一系列脉冲宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码。也就是说通过调节占空比的变化来调节信号、能量等的变化,占空比就是指在一个周期内,信号处于…...

毕业设计 基于51单片机WIFI智能家居系统设计
基于51单片机WIFI智能家居系统设计1、毕业设计选题原则说明(重点)2、项目资料2.1 系统框架2.2 系统功能3、部分电路设计3.1 STC89C52单片机最小系统电路设计3.2 ESP8266 WIFI电路设计3.3 DHT11温湿度传感器电路设计4、部分代码展示4.1 LCD12864显示字符串…...
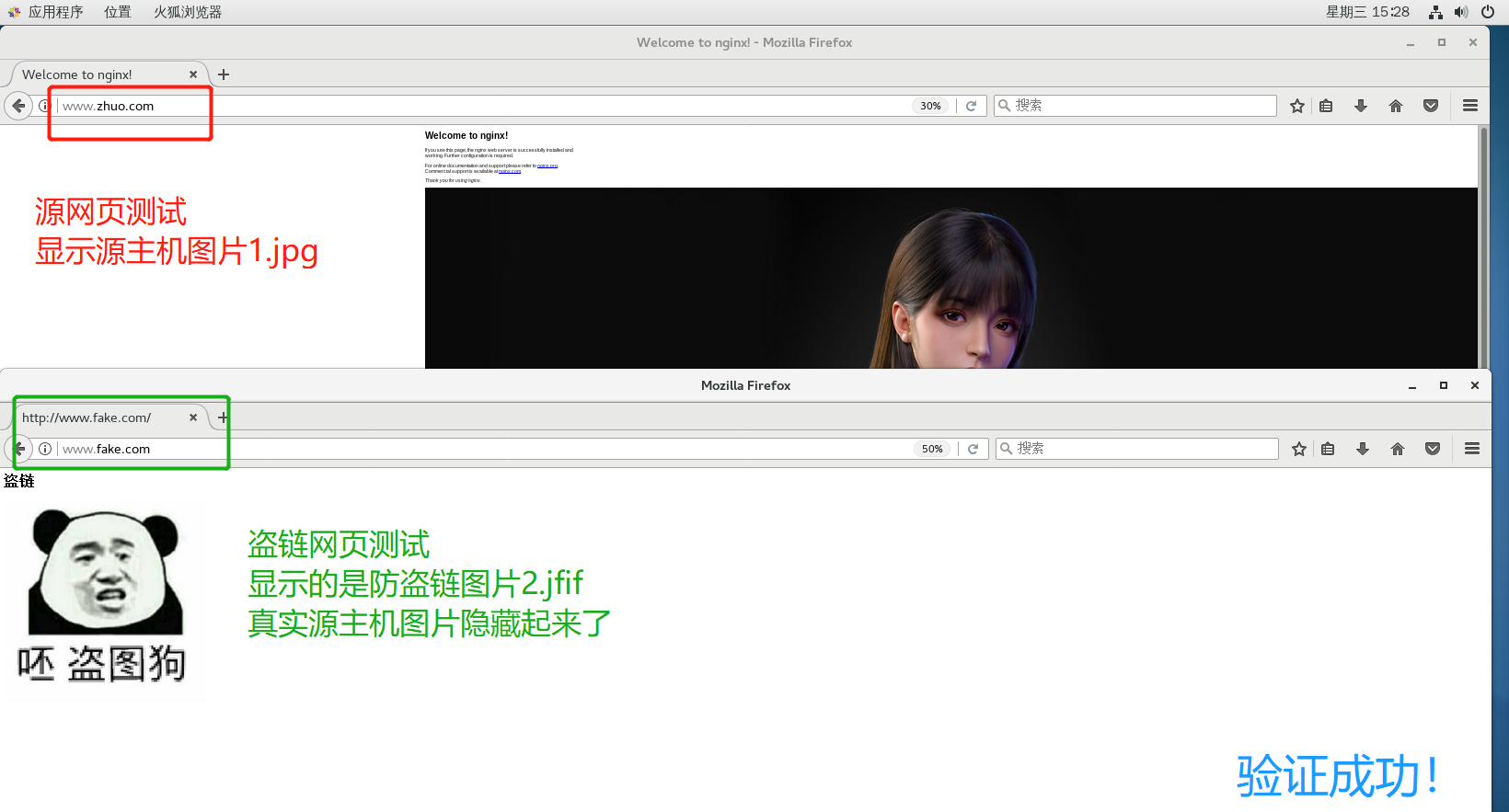
Nginx服务优化措施与配置防盗链
目录 一.优化Nginx的相关措施 二.隐藏/查看版本号 三.修改用户与组 四.设置缓存时间 五.日志切割脚本 六.设置连接超时控制连接访问时间 七.开启多进程 八.配置网页压缩 九.配置防盗链 1.配置web源主机(192.168.79.210 www.zhuo.com) 1.1 安装…...

Java 某厂面试题真题合集
哈喽~大家好,这篇来看看Java 某厂面试题真题合集。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Spr…...

很特别的5G市场,5.75亿部手机,却有11亿5G用户,这是怎么了?
中国在5G商用方面已取得了巨大的成绩,这是毋庸置疑的,不过近期公布的一份数据却相当特别,5G手机用户数为5.75亿,而开通了5G套餐的用户数却已超过11亿,这数据对比有点意思。中国在5G商用方面推进很快,建成的…...

go modules
文章目录1. 简介示例1. 示例——同一项目2. 示例——不同项目3. 示例——添加远程模块依赖库1. 简介 go module是Go1.11版本之后官方推出的版本管理工具,并且从Go1.13版本开始,go module将是Go语言默认的依赖管理工具。到今天Go1.14版本推出之后Go modu…...
Baklib客户故事:快递助手ERP
快递助手ERP以多平台多店铺订单管理为核心,集打单发货、商品、库存、采购、售后于一体,中小商家易上手的轻量级ERP,可以满足满足微商、自建商城、档口货源网、一件代发等不同类型客户的打单需求,通过开放平台API接口,自…...
MongoDB学习(java版)
MongoDB概述 结构化数据库 结构化数据库是一种使用结构化查询语言(SQL)进行管理和操作的数据库,它们的数据存储方式是基于表格和列的。结构化数据库要求数据预先定义数据模式和结构,然后才能存储和查询数据。结构化数据库通常…...

RK3568平台开发系列讲解(显示篇)什么是DRM
🚀返回专栏总目录 文章目录 一、DRM介绍二、DRM与framebuffer的区别沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍什么是DRM。 一、DRM介绍 DRM 是 Linux 目前主流的图形显示框架,相比FB架构,DRM更能适应当前日益更新的显示硬件。 比如FB原生不支…...

Python蓝桥杯训练:基本数据结构 [二叉树] 上
Python蓝桥杯训练:基本数据结构 [二叉树] 上 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 上一、前言二、有关二叉树理论基础1、二叉树的基本定义2、二叉树的常见类型3、二叉树的遍历方式三、有关二叉树的层序遍历的题目1、[二叉树的层序遍历](http…...
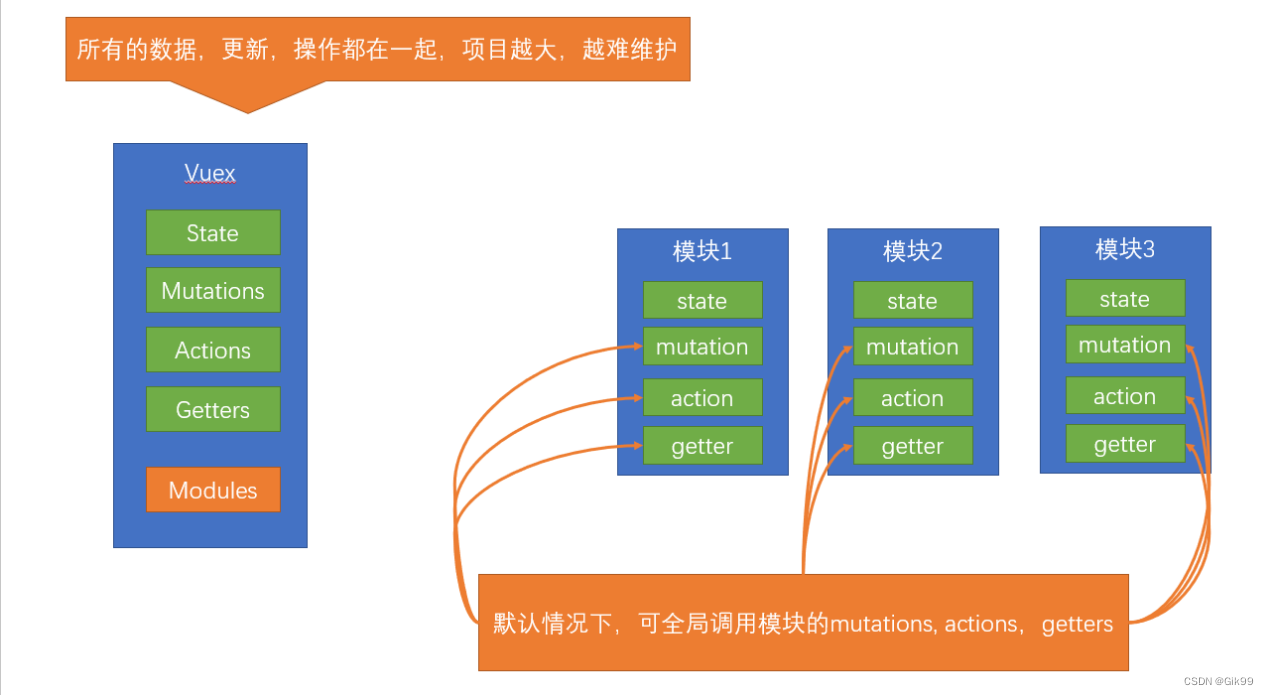
vuex基础之初始化功能、state、mutations、getters、模块化module的使用
vuex基础之初始化功能、state、mutations、getters、模块化module的使用一、Vuex的介绍二、初始化功能三、state3.1 定义state3.2 获取state3.2.1 原始形式获取3.2.2 辅助函数获取(mapState)四、mutations4.1 定义mutations4.2 调用mutations4.2.1 原始形式调用($store)4.2.2 辅…...

WebSphere中间件漏洞总结
WebSphere中间件漏洞总结 一、WebSphere简介 WebSphere为SOA(面向服务架构)环境提供软件,以实现动态的、互联的业务流程,为所有业务情形提供高度有效的应用程序基础架构。WebSphere是IBM的应用程序和集成软件平台,包含所有必要的中间件基础架构(包括服务器、服务和工具)…...

Unity之ASE实现影魔灵魂收集特效
前言 我们今天来实现一下Dota中的影魔死亡后,灵魂收集的特效。效果如下: 实现原理 1.先添加一张FlowMap图,这张图的UV是根据默认UV图,用PS按照我们希望的扭曲方向修改的如下图所示: 2.通过FlowMap图,我…...

半入耳式耳机运动会不会掉、佩戴超稳固的运动耳机推荐
现在越来越多的人开始意识到运动的重要性,用运动给身体增加一道“防护墙”是最好的生活方式了,不过,日复一日做着几乎相同的动作,难免索然无味,所以很多人都会选择在运动时戴上耳机听歌解闷,这时候也有不少…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

C#中用于控制自定义特性(Attribute)
我们来详细解释一下 [AttributeUsage(AttributeTargets.Class, AllowMultiple false, Inherited false)] 这个 C# 属性。 在 C# 中,Attribute(特性)是一种用于向程序元素(如类、方法、属性等)添加元数据的机制。Attr…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...
