Node.js —— 前后端的身份认证 之用 express 实现 JWT 身份认证
JWT的认识
什么是 JWT
JWT(英文全称:JSON Web Token)是目前最流行的跨域认证解决方案。
JWT 的工作原理
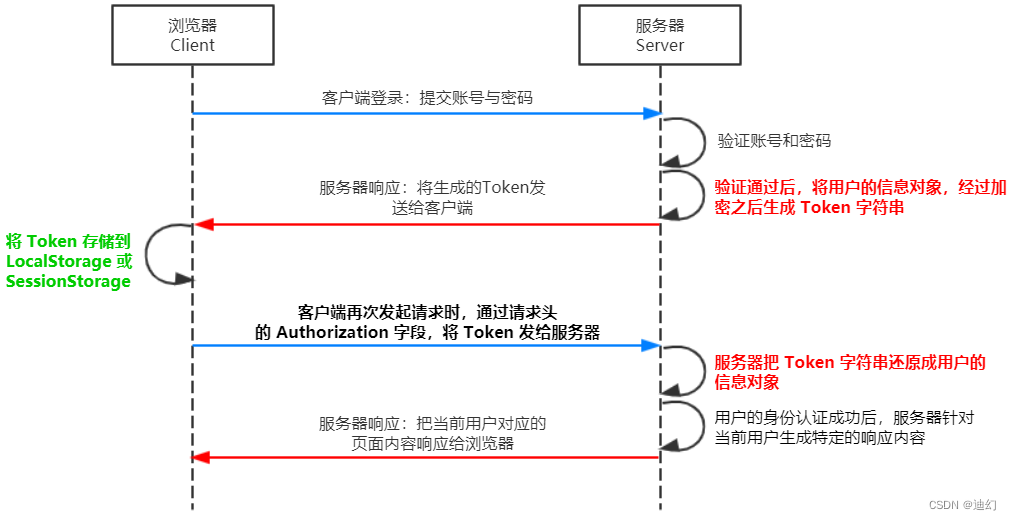
总结:用户的信息通过 Token 字符串的形式,保存在客户端浏览器中。服务器通过还原 Token 字符串的形式来认证用户的身份。
JWT 的组成部分
JWT 通常由三部分组成,分别是 Header(头部)、Payload(有效荷载)、Signature(签名)。 三者之间使用英文的“.”分隔,格式如下:

下面是 JWT 字符串的示例:

JWT 的三个部分各自代表的含义
JWT 的三个组成部分,从前到后分别是
- Header
- Payload
- Signature
其中: Payload 部分才是真正的用户信息,它是用户信息经过加密之后生成的字符串。
Header 和 Signature 是安全性相关的部分,只是为了保证 Token 的安全性。

JWT 的使用方式
客户端收到服务器返回的 JWT 之后,通常会将它储存在 localStorage 或 sessionStorage 中。
此后,客户端每次与服务器通信,都要带上这个 JWT 的字符串,从而进行身份认证。推荐的做法是把 JWT 放在 HTTP 请求头的 Authorization 字段中,格式如下:

在 Express 中使用 JWT
1.安装 JWT 相关的包
运行如下命令,安装如下两个 JWT 相关的包:

其中:
- jsonwebtoken 用于生成 JWT 字符串
- express-jwt 用于将 JWT 字符串解析还原成 JSON 对象
2. 导入 JWT 相关的包
使用 require() 函数,分别导入 JWT 相关的两个包:

3. 定义 secret 密钥
为了保证 JWT 字符串的安全性,防止 JWT 字符串在网络传输过程中被别人破解,我们需要专门定义一个用于加密和解密的 secret 密钥:
- 当生成 JWT 字符串的时候,需要使用 secret 密钥对用户的信息进行加密,最终得到加密好的 JWT 字符串
- 当把 JWT 字符串解析还原成 JSON 对象的时候,需要使用 secret 密钥进行解密
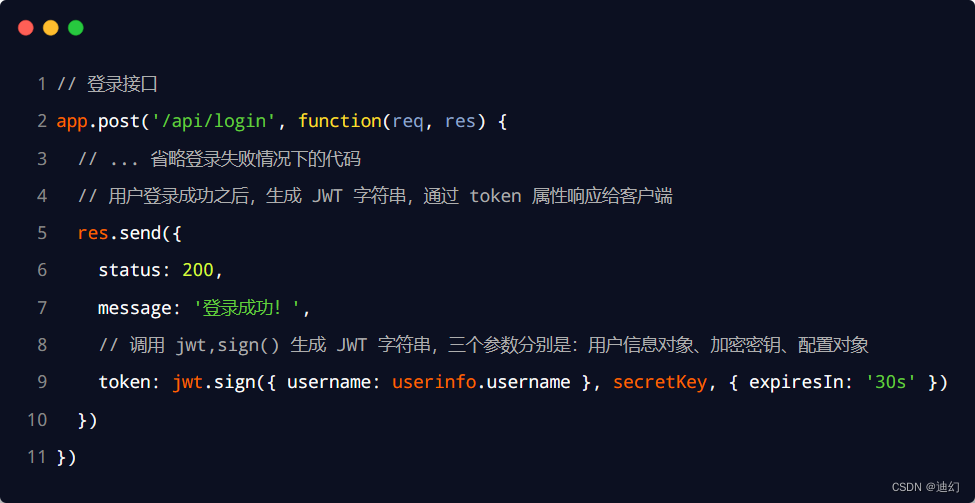
4. 在登录成功后生成 JWT 字符串
调用 jsonwebtoken 包提供的 sign() 方法,将用户的信息加密成 JWT 字符串,响应给客户端:
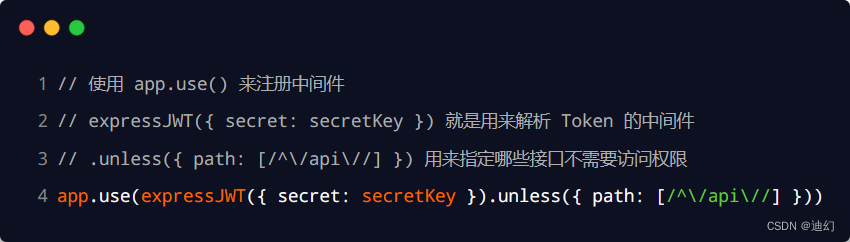
5. 将 JWT 字符串还原为 JSON 对象
客户端每次在访问那些有权限接口的时候,都需要主动通过请求头中的 Authorization 字段,将 Token 字符串发送到服务器进行身份认证。 此时,服务器可以通过 express-jwt 这个中间件,自动将客户端发送过来的 Token 解析还原成 JSON 对象:
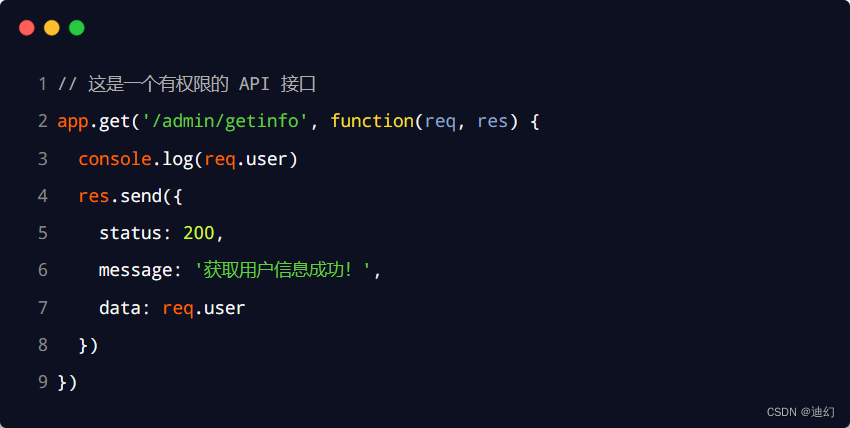
6. 使用 req.user 获取用户信息
当 express-jwt 这个中间件配置成功之后,即可在那些有权限的接口中,使用 req.user 对象,来访问从 JWT 字符串中解析出来的用户信息了,示例代码如下:
相关文章:

Node.js —— 前后端的身份认证 之用 express 实现 JWT 身份认证
JWT的认识 什么是 JWT JWT(英文全称:JSON Web Token)是目前最流行的跨域认证解决方案。 JWT 的工作原理 总结:用户的信息通过 Token 字符串的形式,保存在客户端浏览器中。服务器通过还原 Token 字符串的形式来认证用…...

文旅3d仿真数字人形象为游客提供全方位的便捷服务
在AI人工智能与VR虚拟现实技术的双重驱动下,文旅3D数字代言人正以其独特的魅力,频频亮相于各类文旅场景,为游客带来前所未有的个性化服务体验。他们不仅有趣有品,更能言善道,成为文旅业数字化发展的新亮点。 这些文旅3…...

leetcode算法常用函数
文章目录 字符相关字符串相关数组和集合相关数值相关容器相关 核心关注算法逻辑,其他的常见操作用标准库里函数即可,不用浪费时间。 Java语言作为参考,记录刷题时常用的函数 字符相关 Character.isDigit(); //判断是否为数字Character.isLet…...
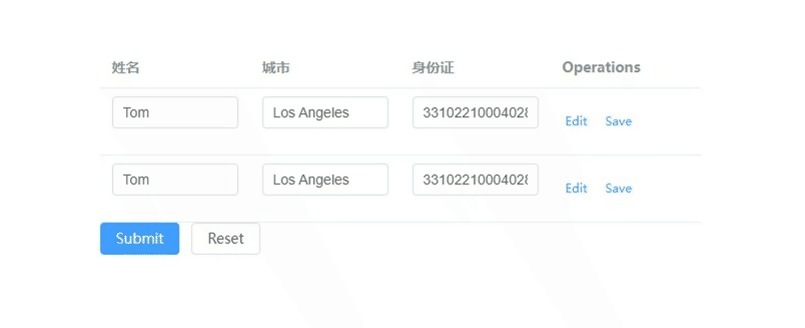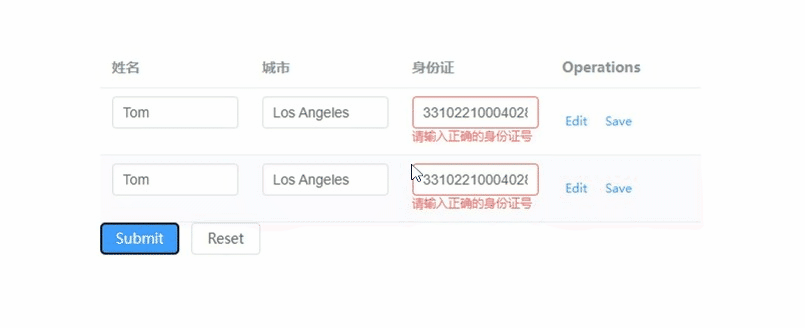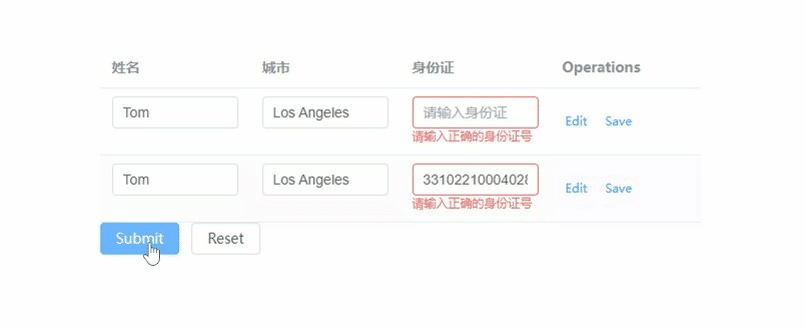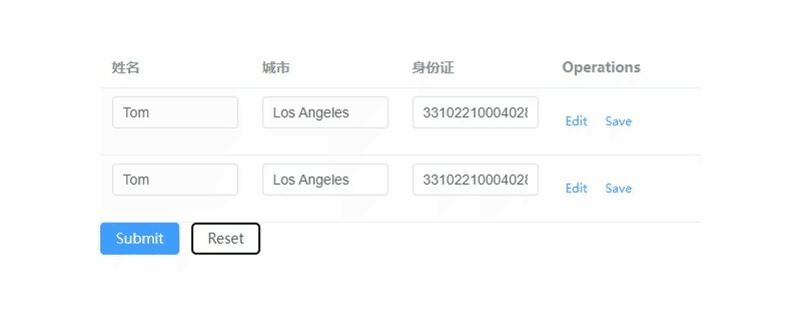
element-plus表格的表单校验如何实现,重点在model和prop
文章目录 vue:3.x element-plus:2.7.3 重点: 1) tableData放到form对象里 2) form-item的prop要写成tableData.序号.属性 <!--table-表单校验--> <template><el-form ref"forms" :model"form"><e…...

WPF密码输入框明文掩码切换
1,效果 2,代码: WPF的PasswordBox不能像Winform中的PasswordBox那样,通过PasswordBox.PasswordChar(char)0显示明文。所以这里使用无外观控件构筑掩码明文切换。 无外观控件遵守Themes/Generic.xaml文件配置. <ResourceDicti…...

SaaS架构详细介绍及一个具体实现的示例
SaaS架构详细介绍 软件即服务(SaaS,Software as a Service)是一种通过互联网交付软件应用程序的模式。 SaaS提供商托管应用程序,并通过网络将其提供给最终用户,用户无需安装和维护软件,只需通过浏览器或其他…...

四川音盛佳云电子商务有限公司正规吗?靠谱吗?
在数字化浪潮席卷全球的今天,电子商务已成为推动经济发展的重要引擎。四川音盛佳云电子商务有限公司,作为抖音电商服务的佼佼者,正以其独特的视角和创新的策略,引领着抖音电商的新潮流,开启着电商服务的新篇章。 四川…...
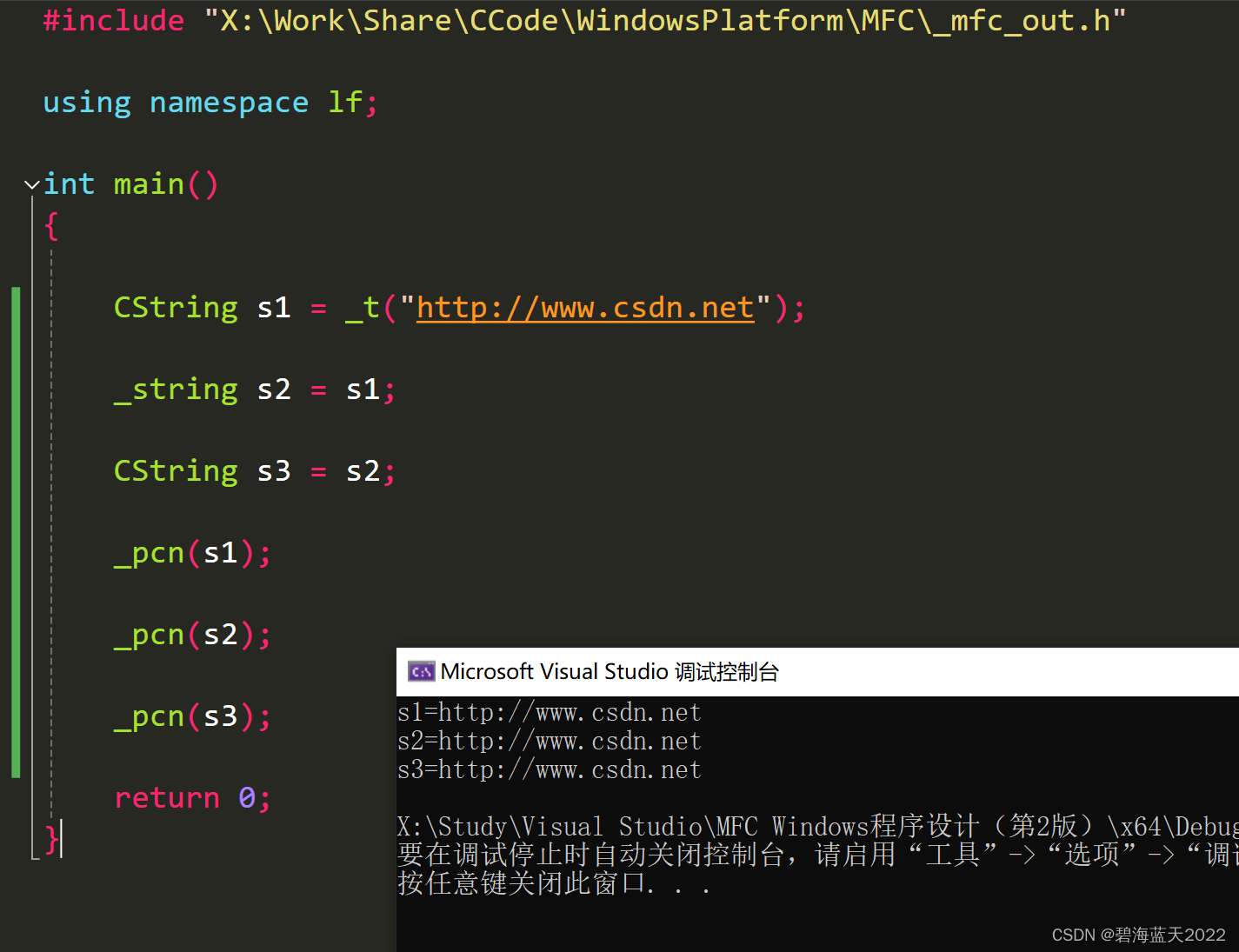
C++ 写的_string类,兼容std::string, MFC CString和 C# 的string
代码例子: using namespace lf; int main() { CString s1 _t("http://www.csdn.net"); _string s2 s1; CString s3 s2; _pcn(s1); _pcn(s2); _pcn(s3); return 0; } 输出: _Str.h /***************************************…...

【揭开深度学习之核:反向传播算法简析】
文章目录 前言反向传播算法的基础工作原理伪代码示例关键点结论 前言 在深度学习的世界里,反向传播算法是一张藏在神秘面纱后的地图,它指引着神经网络通过复杂的数据迷宫,找到最优解的路径。本文将简要介绍反向传播算法的原理,探…...

Web3 知识体系架构图
Web3 知识体系架构图 │ ├── 1. 基础概念 │ │ │ ├── 1.1 区块链 │ │ ├── 工作原理 │ │ ├── 公链 vs 私链 │ │ └── 常见区块链平台(如比特币、以太坊) │ │ │ ├── 1.2 去中心化 │ │ ├── P2P 网络 │ │ ├── 去中心化…...

SQL、Mongo、Redis一般适用于那些场景
在一个项目中同时使用 MySQL、Redis 和 MongoDB 是相对常见的做法,因为它们各自具有不同的特点和适用场景,可以组合使用以满足不同的需求。下面是它们的一些常见用途和特点: MySQL: 关系型数据库: MySQL 是一个传统的关…...

学习图形推理
学习图形推理 1.位置规律1.1平移1.2翻转、旋转2.样式规律2.1加减异同2.2黑白运算3.属性规律3.1对称性3.2曲直性3.3开闭性4.数量规律4.1面4.2线数量4.3笔画数4.4点数量4.5素数量5.空间重构5.1相对面5.2相邻面-公共边5.3相邻面-公共点5.4相邻面-画边法题型 一组图:从左往右找规律…...

plsql 学习
过程化编程语言 赋值:: ||:连接符号 dbms_output.put_line() :输出的语句 var_name ACCOUNTLIBRARY.USERNAME%type; 变量名;某个表的数据类型;赋值给变量名 用下面的方法更好用 异常exception 循…...

如何远程连接默认端口?
远程连接是指通过网络实现两个或多个计算机之间的连接和通信。在进行远程连接时,使用的端口号是一个重要的参数。端口号是计算机上正在运行的特定应用程序的标识符。每个应用程序都会监听一个或多个特定的端口号,以便接收来自其他计算机的连接请求&#…...

现代C++ 如何使用 Lambda 使代码更具表现力、更容易理解?
使用 Lambda 使代码更具表现力 一、Lambda VS. 仿函数二、总结 一、Lambda VS. 仿函数 Lambda 是 C11 中最引人注目的语言特性之一。它是一个强大的工具,但必须正确使用才能使代码更具表现力,而不是更难理解。 首先,要明确的是,…...
)
LeetCode 2644.找出可整除性得分最大的整数:暴力模拟(两层循环)
【LetMeFly】2644.找出可整除性得分最大的整数:暴力模拟(两层循环) 力扣题目链接:https://leetcode.cn/problems/find-the-maximum-divisibility-score/ 给你两个下标从 0 开始的整数数组 nums 和 divisors 。 divisors[i] 的 …...

Python列表,元组,集合,字典详解一篇搞懂
目录 介绍 列表(List) 集合(Set) 字典(Dict) 元组(Tuple) 列表 列表定义 编辑 列表切片 列表常用方法 append extend 编辑 insert 编辑 remove pop 编辑 clear 编辑 列表修改元素 sort 升序 倒序 reverse count 编辑 index 浅拷贝和深拷贝 …...
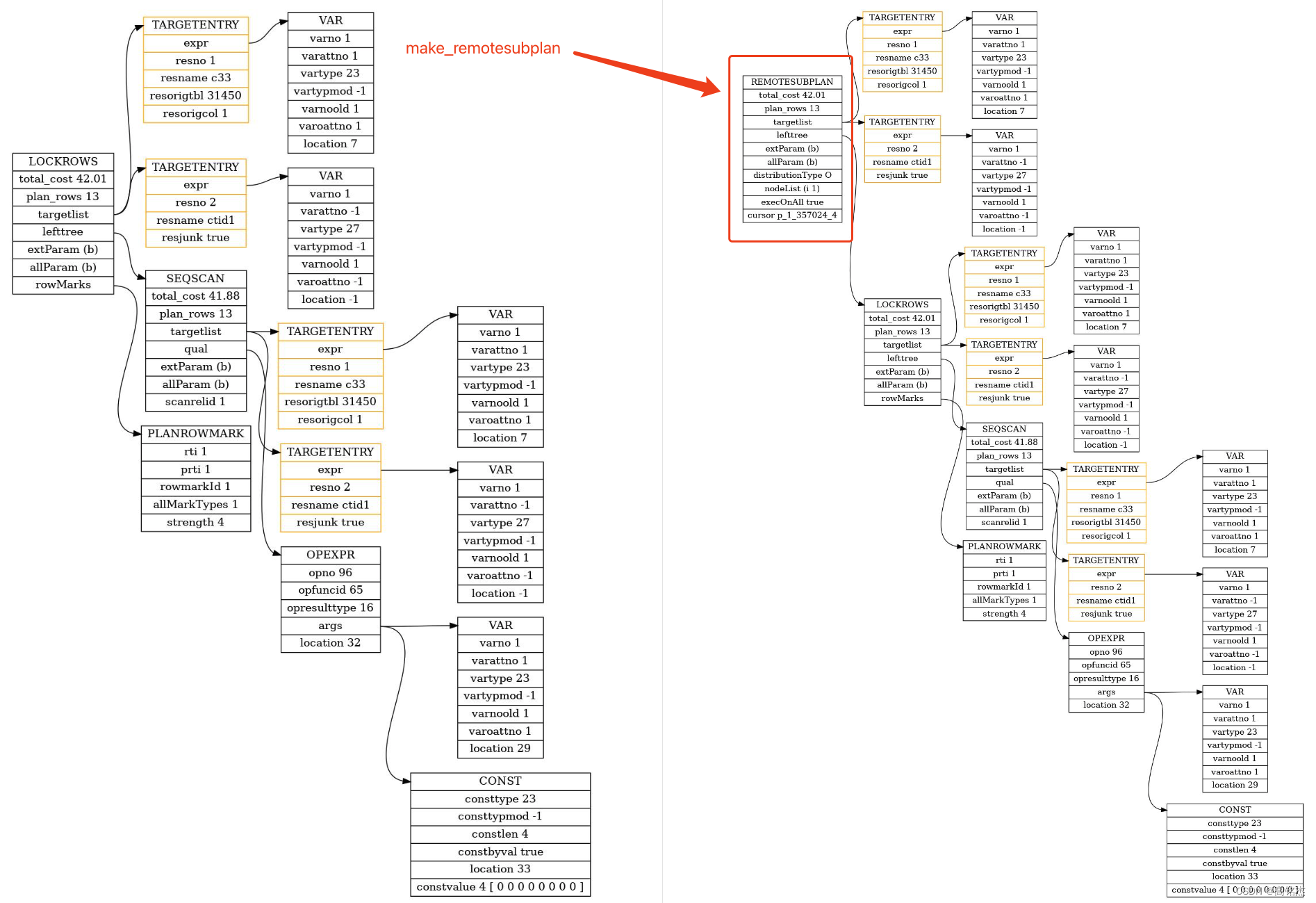
Postgresql源码(132)分布式行锁的原理分析
相关 《Postgresql源码(131)行锁的原理分析》 1 分布式行锁 PG中的行锁在上一片中做了分析《Postgresql源码(131)行锁的原理分析》,本篇对分布式PG(PGXL)中的行锁做一些分析。(版本…...

前端 防抖和节流
在前端开发中,防抖(Debounce)和节流(Throttle)是两种常用的性能优化技术,尤其在处理频繁触发的事件时显得尤为重要。无论是在用户输入、窗口调整大小,还是滚动事件中,这两种技术都可…...
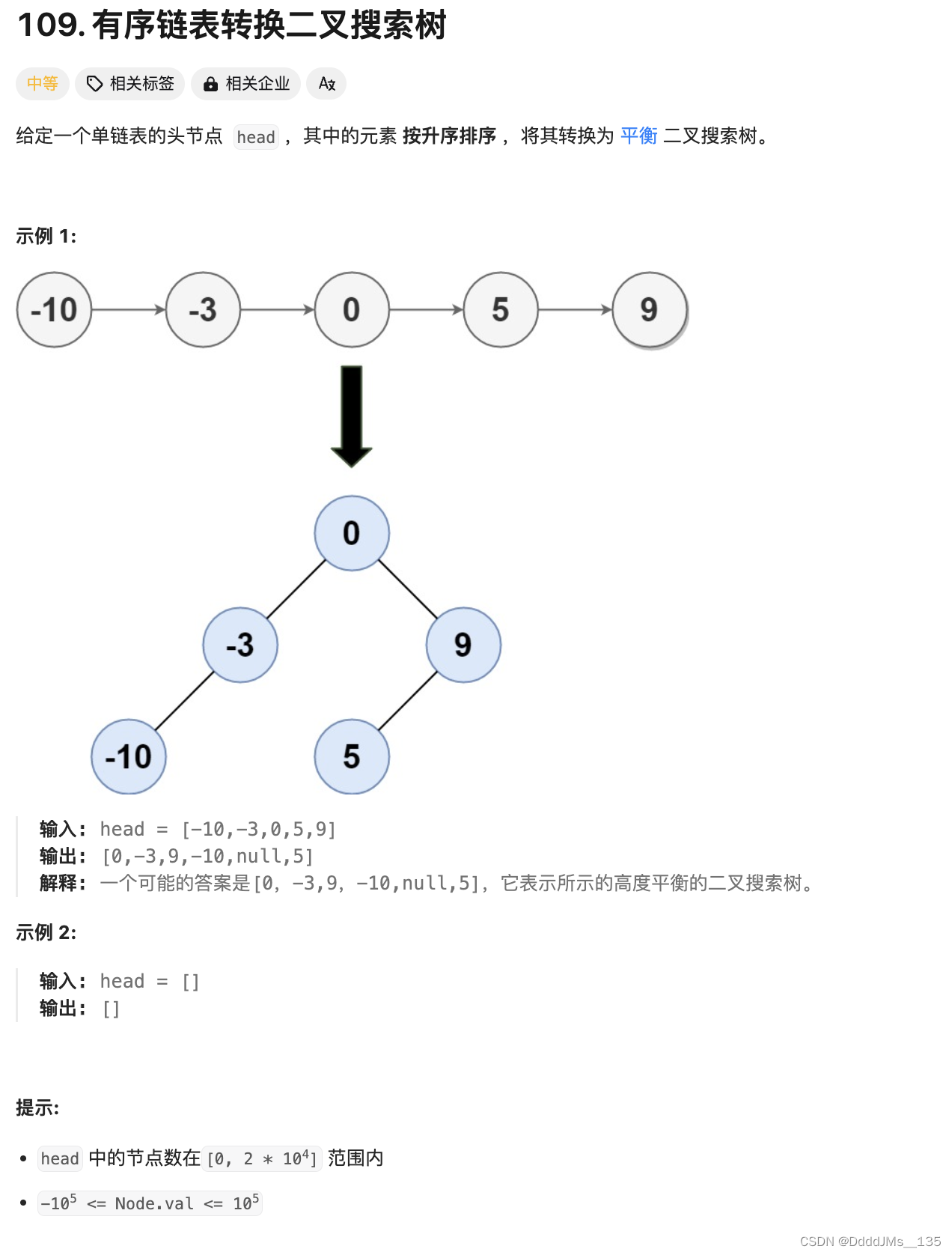
C语言 | Leetcode C语言题解之第109题有序链表转换二叉搜索树
题目: 题解: int getLength(struct ListNode* head) {int ret 0;while (head ! NULL) {ret, head head->next;}return ret; }struct TreeNode* buildTree(struct ListNode** head, int left, int right) {if (left > right) {return NULL;}int …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
