秋招突击——算法——模板题——区间DP——合并石子
文章目录
- 题目内容
- 思路分析
- 实现代码
- 分析与总结
题目内容

思路分析
- 基本思路,先是遍历区间长度,然后再是遍历左端点,最后是遍历中间的划分点,将阶乘问题变成n三次方的问题


实现代码
// 组合数问题
#include <iostream>
#include <algorithm>
using namespace std;const int N = 310; // 天数,数组的长度
int w[N],s[N]; // 分别用来存储对应的数字和对应的累加和
int f[N][N]; // f[i][j]区间i到j的最小的花费
int n;int main(){cin>>n; // 获取石子的堆数// 计算前缀和for(int i = 1;i <= n ;i++) {cin>>w[i];s[i] = s[i - 1] + w[i];}// 遍历区间长度,区间为1,不用遍历for (int len = 2; len <= n; ++len) {// 遍历区间的起点,上限是:起点加上区间长度,没有超过nfor (int i = 1; i + len - 1<= n; ++i) {int j = i + len - 1;f[i][j] = 1e8;// 遍历区间内的分割点,最小值和最大值只要取一个,理论上都是一样的for (int k = i; k < j; ++k) {f[i][j] = min(f[i][j],f[i][k] + f[k + 1][j] + s[j] - s[i - 1] );}}}cout<<f[1][n]<<endl;return 0;
}
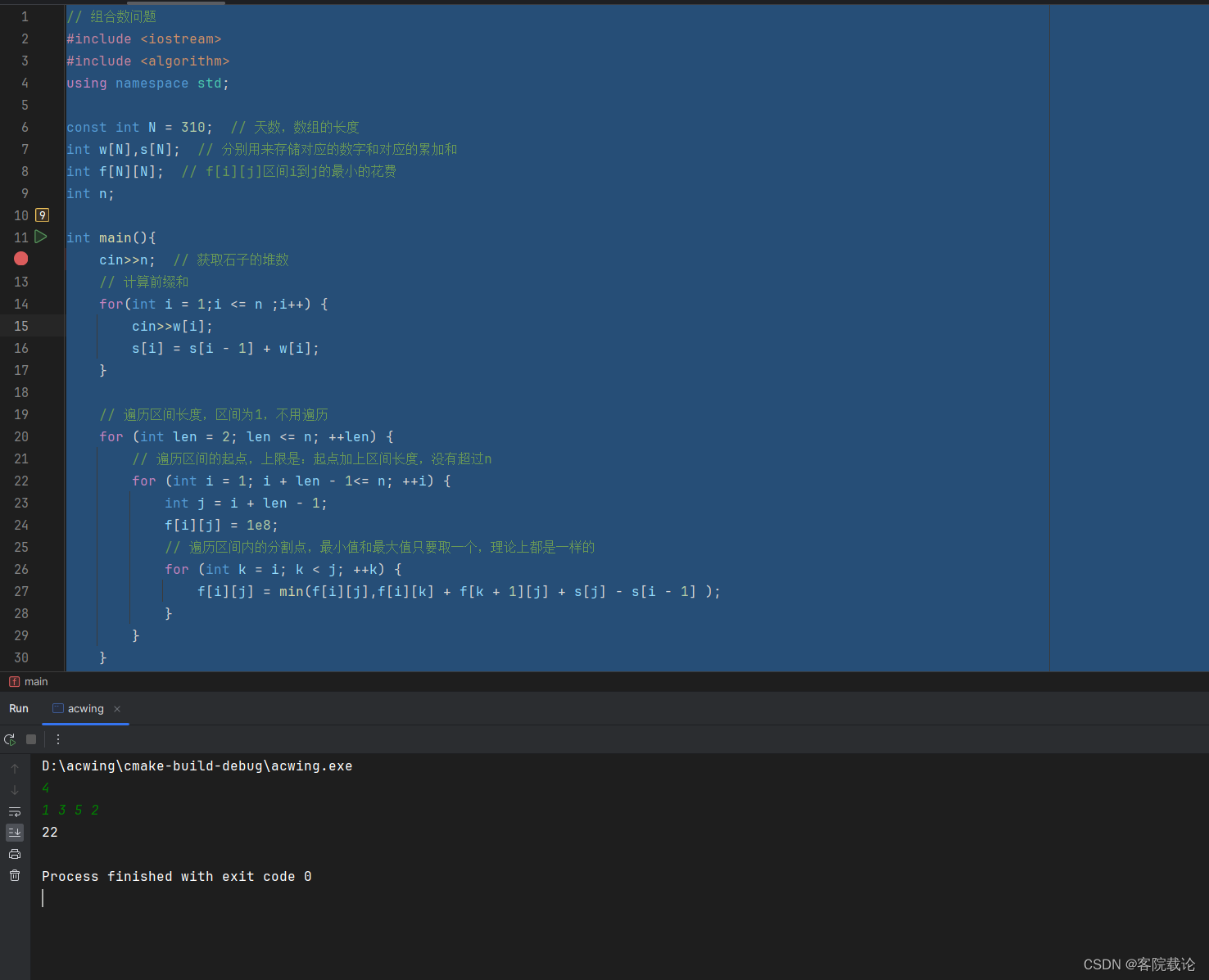
分析与总结
- 这里有个很重要的问题,就是把i和j想象成区间的起点和重点,这个我就没想到。是这样分析的,如果能够组成堆,因为相邻的,所以肯定是i和j这个区间连续内部可以组成堆。然后在不断进行拆分。
相关文章:

秋招突击——算法——模板题——区间DP——合并石子
文章目录 题目内容思路分析实现代码分析与总结 题目内容 思路分析 基本思路,先是遍历区间长度,然后再是遍历左端点,最后是遍历中间的划分点,将阶乘问题变成n三次方的问题 实现代码 // 组合数问题 #include <iostream> #in…...

数据库——实验12 数据库备份和还原
1. 备份设备的概念和方法 备份设备是指 SQL Server 中存储数据库和事务日志备份副本的载体,备份设备可以被定义成本地的磁盘文件、远程服务器上的磁盘文件、磁带。 在创建备份时,必须选择要将数据写入的备份设备。SQL Server 2005 可以将数据库、事务日…...
Node.js —— 前后端的身份认证 之用 express 实现 JWT 身份认证
JWT的认识 什么是 JWT JWT(英文全称:JSON Web Token)是目前最流行的跨域认证解决方案。 JWT 的工作原理 总结:用户的信息通过 Token 字符串的形式,保存在客户端浏览器中。服务器通过还原 Token 字符串的形式来认证用…...

文旅3d仿真数字人形象为游客提供全方位的便捷服务
在AI人工智能与VR虚拟现实技术的双重驱动下,文旅3D数字代言人正以其独特的魅力,频频亮相于各类文旅场景,为游客带来前所未有的个性化服务体验。他们不仅有趣有品,更能言善道,成为文旅业数字化发展的新亮点。 这些文旅3…...

leetcode算法常用函数
文章目录 字符相关字符串相关数组和集合相关数值相关容器相关 核心关注算法逻辑,其他的常见操作用标准库里函数即可,不用浪费时间。 Java语言作为参考,记录刷题时常用的函数 字符相关 Character.isDigit(); //判断是否为数字Character.isLet…...
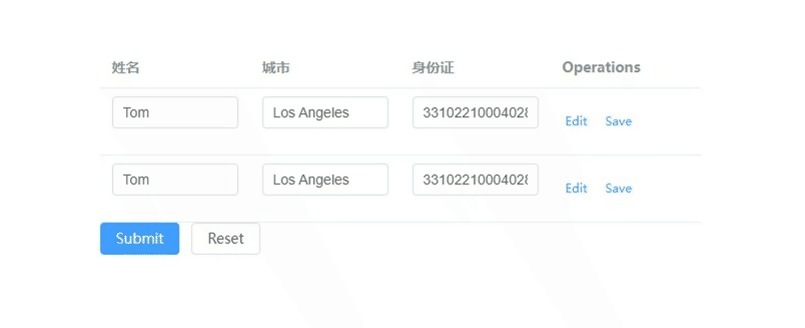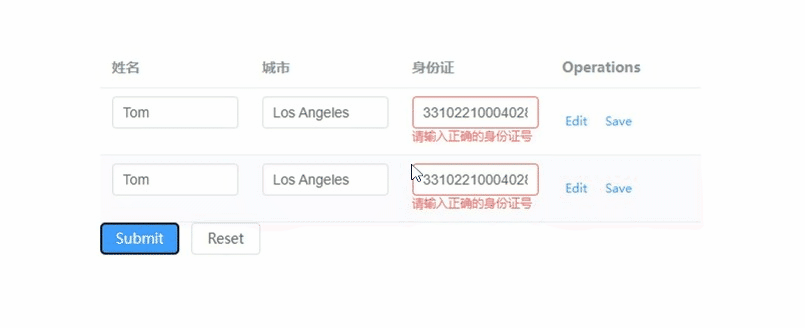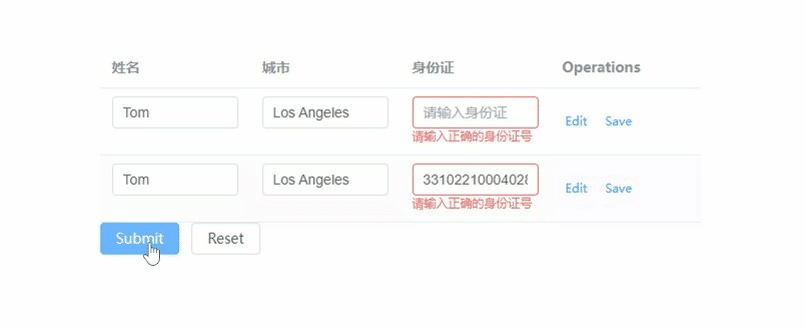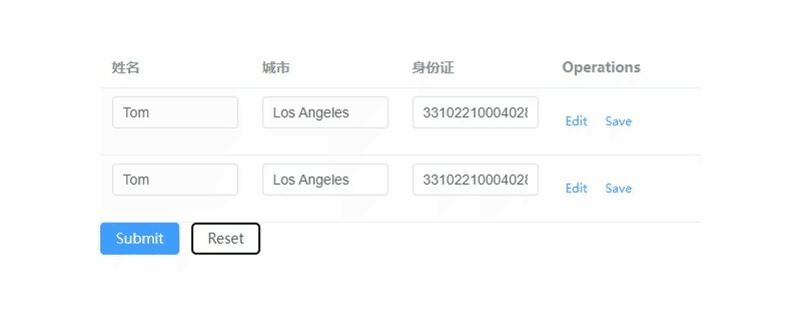
element-plus表格的表单校验如何实现,重点在model和prop
文章目录 vue:3.x element-plus:2.7.3 重点: 1) tableData放到form对象里 2) form-item的prop要写成tableData.序号.属性 <!--table-表单校验--> <template><el-form ref"forms" :model"form"><e…...

WPF密码输入框明文掩码切换
1,效果 2,代码: WPF的PasswordBox不能像Winform中的PasswordBox那样,通过PasswordBox.PasswordChar(char)0显示明文。所以这里使用无外观控件构筑掩码明文切换。 无外观控件遵守Themes/Generic.xaml文件配置. <ResourceDicti…...

SaaS架构详细介绍及一个具体实现的示例
SaaS架构详细介绍 软件即服务(SaaS,Software as a Service)是一种通过互联网交付软件应用程序的模式。 SaaS提供商托管应用程序,并通过网络将其提供给最终用户,用户无需安装和维护软件,只需通过浏览器或其他…...

四川音盛佳云电子商务有限公司正规吗?靠谱吗?
在数字化浪潮席卷全球的今天,电子商务已成为推动经济发展的重要引擎。四川音盛佳云电子商务有限公司,作为抖音电商服务的佼佼者,正以其独特的视角和创新的策略,引领着抖音电商的新潮流,开启着电商服务的新篇章。 四川…...
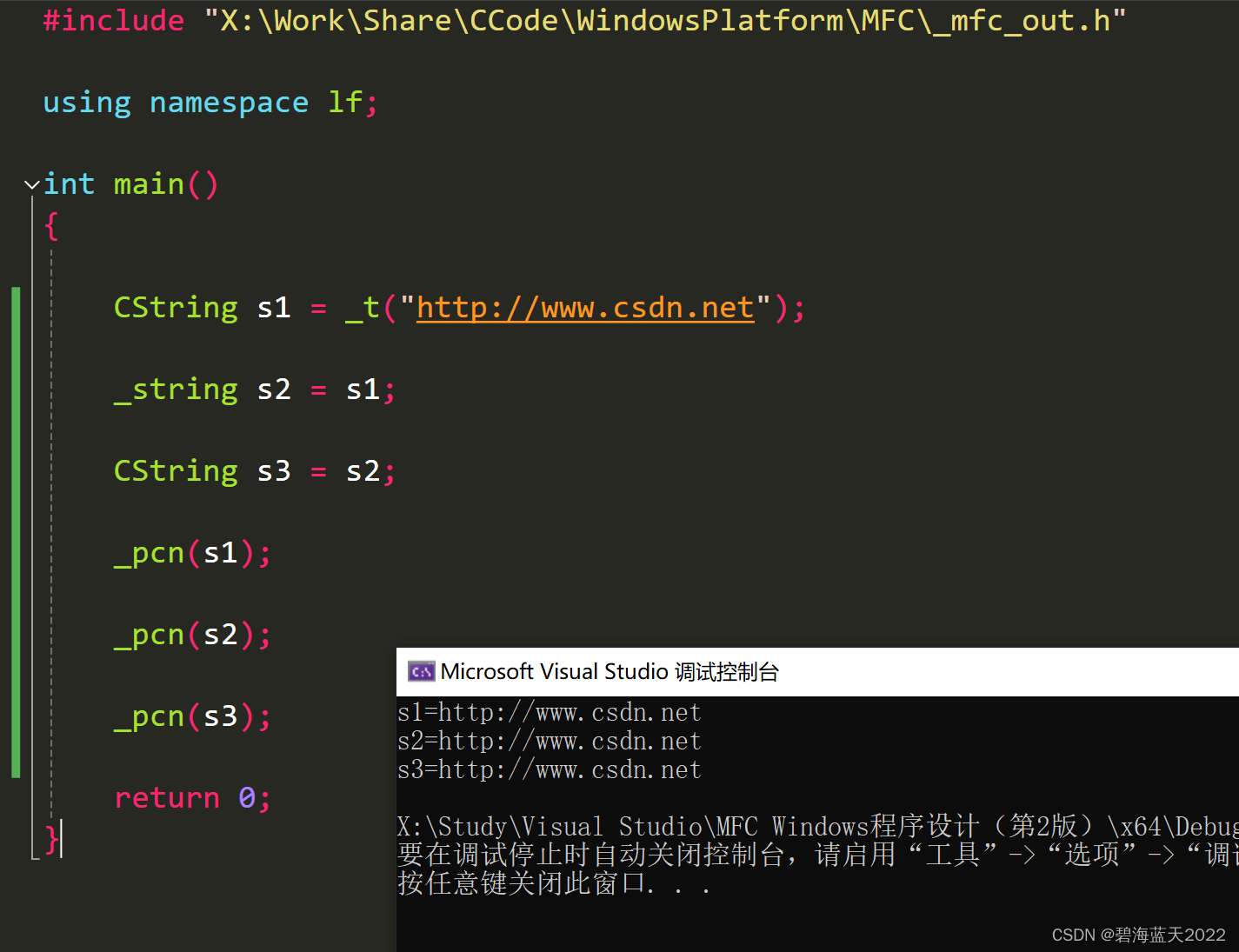
C++ 写的_string类,兼容std::string, MFC CString和 C# 的string
代码例子: using namespace lf; int main() { CString s1 _t("http://www.csdn.net"); _string s2 s1; CString s3 s2; _pcn(s1); _pcn(s2); _pcn(s3); return 0; } 输出: _Str.h /***************************************…...

【揭开深度学习之核:反向传播算法简析】
文章目录 前言反向传播算法的基础工作原理伪代码示例关键点结论 前言 在深度学习的世界里,反向传播算法是一张藏在神秘面纱后的地图,它指引着神经网络通过复杂的数据迷宫,找到最优解的路径。本文将简要介绍反向传播算法的原理,探…...

Web3 知识体系架构图
Web3 知识体系架构图 │ ├── 1. 基础概念 │ │ │ ├── 1.1 区块链 │ │ ├── 工作原理 │ │ ├── 公链 vs 私链 │ │ └── 常见区块链平台(如比特币、以太坊) │ │ │ ├── 1.2 去中心化 │ │ ├── P2P 网络 │ │ ├── 去中心化…...

SQL、Mongo、Redis一般适用于那些场景
在一个项目中同时使用 MySQL、Redis 和 MongoDB 是相对常见的做法,因为它们各自具有不同的特点和适用场景,可以组合使用以满足不同的需求。下面是它们的一些常见用途和特点: MySQL: 关系型数据库: MySQL 是一个传统的关…...

学习图形推理
学习图形推理 1.位置规律1.1平移1.2翻转、旋转2.样式规律2.1加减异同2.2黑白运算3.属性规律3.1对称性3.2曲直性3.3开闭性4.数量规律4.1面4.2线数量4.3笔画数4.4点数量4.5素数量5.空间重构5.1相对面5.2相邻面-公共边5.3相邻面-公共点5.4相邻面-画边法题型 一组图:从左往右找规律…...

plsql 学习
过程化编程语言 赋值:: ||:连接符号 dbms_output.put_line() :输出的语句 var_name ACCOUNTLIBRARY.USERNAME%type; 变量名;某个表的数据类型;赋值给变量名 用下面的方法更好用 异常exception 循…...

如何远程连接默认端口?
远程连接是指通过网络实现两个或多个计算机之间的连接和通信。在进行远程连接时,使用的端口号是一个重要的参数。端口号是计算机上正在运行的特定应用程序的标识符。每个应用程序都会监听一个或多个特定的端口号,以便接收来自其他计算机的连接请求&#…...

现代C++ 如何使用 Lambda 使代码更具表现力、更容易理解?
使用 Lambda 使代码更具表现力 一、Lambda VS. 仿函数二、总结 一、Lambda VS. 仿函数 Lambda 是 C11 中最引人注目的语言特性之一。它是一个强大的工具,但必须正确使用才能使代码更具表现力,而不是更难理解。 首先,要明确的是,…...
)
LeetCode 2644.找出可整除性得分最大的整数:暴力模拟(两层循环)
【LetMeFly】2644.找出可整除性得分最大的整数:暴力模拟(两层循环) 力扣题目链接:https://leetcode.cn/problems/find-the-maximum-divisibility-score/ 给你两个下标从 0 开始的整数数组 nums 和 divisors 。 divisors[i] 的 …...

Python列表,元组,集合,字典详解一篇搞懂
目录 介绍 列表(List) 集合(Set) 字典(Dict) 元组(Tuple) 列表 列表定义 编辑 列表切片 列表常用方法 append extend 编辑 insert 编辑 remove pop 编辑 clear 编辑 列表修改元素 sort 升序 倒序 reverse count 编辑 index 浅拷贝和深拷贝 …...
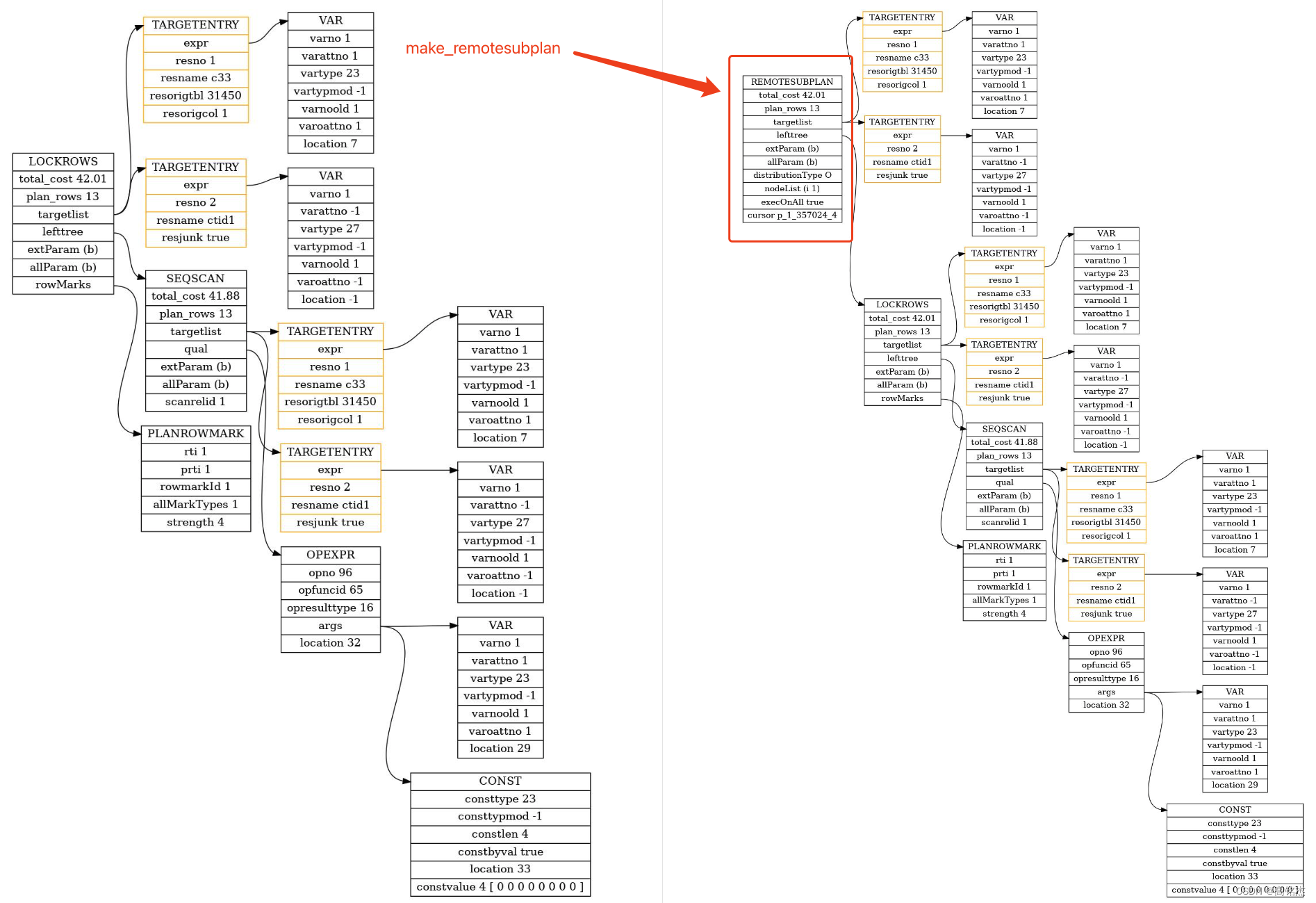
Postgresql源码(132)分布式行锁的原理分析
相关 《Postgresql源码(131)行锁的原理分析》 1 分布式行锁 PG中的行锁在上一片中做了分析《Postgresql源码(131)行锁的原理分析》,本篇对分布式PG(PGXL)中的行锁做一些分析。(版本…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
