回溯大法总结
前言
本篇博客将分两步来进行,首先谈谈我对回溯法的理解,然后通过若干道题来进行讲解,最后总结
对回溯法的理解
回溯法可以看做蛮力法的升级版,它在解决问题时的每一步都尝试所有可能的选项,最终找出所以可行的方案。回溯法非常适合解决由多个步骤组成的问题,并且每个步骤都有多个选项,在每一步选择了其中一个选项之后,就进入下一步,然后又会面临新的选项,就这样重复选择,直至最终的状态。
用回溯法解决问题的过程可以形象地用一个树形结构表示,求解问题的每个步骤可以看作树中的一个节点。如果在某一步有n个可能的选项,每个选项是树中的一条边,经过这些边就可以到达该节点的个子节点。
在采用回溯法解决问题时如果到达树形结构的叶节点,就找到了问题的一个解。如果希望找到更多的解,那么还可以回溯到它的父节点再次尝试父节点其它的选项。如果父节点所有可能的选项都已经试过,那么再回溯到父节点的父节点以尝试它的其他选项,这样逐层回溯到树的根节点。因此,采用回溯法解决问题的过程实质上是在树形结构中从根节点开始进行深度优先遍历。通常,回溯法的深度优先遍历用递归代码实现。
由于回溯法是在所有选项形成的树上进行深度优先遍历,如果解决问题的步骤比较多或每个步骤都面临多个选项,那么遍历整棵树将需要较多的时间,如果明确知道某些子树没有必要遍历,那么在遍历的时候应该避开这些子树以优化效率。通常将使用回溯法时避免遍历不必要的子树的方法称为剪枝。
用回溯解决集合的组合,排列问题
组合不看重元素顺序,因此两个集合中元素个数相同,各元素个数相同,这两个集合就是一个组合。
排列看重元素顺序,因此两个集合中元素个数相同,各元素个数相同,但是元素顺序不同的话,这两个集合就是两个不同的排列。
所有子集
题目

分析
以集合【1,2】为例,有两个元素,每个元素都面临选和不选两种选择,树形图如下图所示:

本题中生成一个子集,可分为若干步,并且每一步都面临若干选择,这正是采用回溯法的典型场景。
代码
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<int> cnums;vector<vector<int>> subsets(vector<int>& nums) {cnums=nums;dfs(0);return vv;}void dfs(int pos){if(pos==cnums.size()){vv.push_back(v);return;}dfs(pos+1);v.push_back(cnums[pos]);dfs(pos+1);v.pop_back();}
};在回溯到父节点时,清除之前相应的修改,即恢复现场。
包含K个元素的组合
题目

分析
集合的一个组合也是一个子集,因此求集合的组合的过程和求子集的过程是一样的,这个题目较钱一道题只是增加了一个限制条件,即只找出包含K个数字的组合,只需要在前一道题的基础上稍加修改即可,就可以找出所有包含K个数字的组合。
代码
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<vector<int>> combine(int n, int k) {dfs(n,k,1);return vv;}void dfs(int n,int k,int pos){if(v.size()==k){vv.push_back(v);return;}if(pos<=n){dfs(n,k,pos+1);v.push_back(pos);dfs(n,k,pos+1);v.pop_back();}}
};允许重复选择元素的组合
题目


分析
这个题目仍然是关于组合的,但组合中的一个数字可以出现任意次,可以以不变应万变,用回溯法来解决这个问题。
能够用回溯法解决的问题都能够分成若干步来解决,每一步都面临若干选择。对于从集合中选取数字组成组合的问题而言,集合中有多少个数字,解决这个问题就需要多少步,每一步都从集合中取出一个下标为i的数字,此时面临两个选择。一个选择是跳过这个数字不将该数字添加到组合中,那么这一步实际上什么都不做,接下来处理下标为i+1的数字。另一个选择是将该数字添加到组合中,由于一个数字可以重复在集合中出现,也就是说,下一步可能再次选择同一个数字,因此下一步仍然处理下标为i的数字。
代码
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {helper(candidates,target,0);return vv;}void helper(vector<int>& candidates, int target,int pos){if(target==0){vv.push_back(v);return;}else if(pos<candidates.size() && target>0){helper(candidates,target,pos+1);v.push_back(candidates[pos]);helper(candidates,target-candidates[pos],pos);v.pop_back();}}
};应用回溯法解决问题时如果有可能应尽可能剪枝以优化时间效率。由于题目明确指出数组中的所有数字都是正整数,因此当组合中已有数字之和已经大于目标值时(即递归函数helper的参数target的值小于0时)就没必要再考虑数组中还没有处理的数字,因为再在组合中添加任意正整数元素之后和会更大,一定找不到新的符合条件的组合,也就没必要再继续尝试,这就是函数helper中else if的条件中补充了一个target大于0的判断条件的原因。
包含重复元素集合的组合
题目


分析
这个题目和之前几个题目与组合相关的题目相比,最大的不同之处在于输入的集合中有重复的数字但输出不得包含重复的组合,如果输入的集合中有重复的数字,不经过特殊处理将产生重复的集合。
避免重复的组合的方法就是当在某一步决定跳过某个值为m的数字时,跳过所有值为m的数字。
为了方便跳过后面所有值相同的数字,可以将集合中的数字排序,将相同的数字放在一起,这样方便比较数字。当决定跳过某个值的数字时,可以按顺序扫描后面的数字,直到找到不同的只为止。
代码
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());helper(candidates,target,0);return vv;}void helper(vector<int>& candidates, int target,int pos){if(target==0){vv.push_back(v);return;}else if(pos<candidates.size() && target>0){int next=pos;while(next<candidates.size() && candidates[next]==candidates[pos]) next++;helper(candidates,target,next);v.push_back(candidates[pos]);helper(candidates,target-candidates[pos],pos+1);v.pop_back();}}
};没有重复元素集合的全排列
题目

分析
假设集合有n个元素,那么生成一个全排列需要n步,当生成排列的第一个数字时会面临n个选项,即n个数字都有可能成为排列的第1个数字,生成排列的第二个数字会面临n-1个选项,即剩下的n-1个数字都有可能成为排列的第2个数字,以此类推。看起来解决这个问题可以分为n步,每一步都面临若干选项,这就是典型的适用回溯法的场景。
方法一
使用一个bool类型数组来标记是否被访问过,每次填写排列的第I个位置时,都从前往后一次遍历没有被访问过的数字,加入排列。
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<int> cpnums;bool vis[10];vector<vector<int>> permute(vector<int>& nums) {cpnums=nums;helper(0);return vv;}void helper(int pos){if(pos==cpnums.size()){vv.push_back(v);return;}for(int i=0;i<cpnums.size();i++){if(!vis[i]){v.push_back(cpnums[i]);vis[i]=true;helper(pos+1);vis[i]=false;v.pop_back();}}}
};方法二
排列和组合不同,排列与元素顺序相关,交换数字能够得到不同的排列,生成全排列的过程,就是交换输入集合中元素的顺序以得到不同的排列。
class Solution {
public:vector<vector<int>> vv;vector<int> cpnums;int n;vector<vector<int>> permute(vector<int>& nums) {cpnums=nums;n=cpnums.size();helper(0);return vv;}void helper(int pos){if(pos==n){vector<int> v;for(int x:cpnums)v.push_back(x);vv.push_back(v);}else{for(int i=pos;i<n;i++){Swap(&cpnums[pos],&cpnums[i]);helper(pos+1);Swap(&cpnums[pos],&cpnums[i]);}}}void Swap(int* a,int* b){int tmp=*a;*a=*b;*b=tmp;}
};包含重复元素集合的全排列
题目

分析
如果集合中有重复的数字,那么交换集合中重复的数字得到的全排列是同一个全排列,例如交换[1,1,2]中的两个数字1并不能得到新的全排列。
为了便于解决有重复元素会出现相同排列问题,先将数组的元素进行排序。
方法一

易知,以红色区域为根节点的子树应该剪掉,但是以绿色区域为根节点的子树是正确的,那么怎么区分二者那?
通过观察不难发现,绿色区域中,目前已填的元素a与前一个元素相同,且前一个元素已经被访问过了,但是红色区域中,目前已填的元素与前一个元素相同,但是前一个元素没有被访问过,这个点就是突破口。
以nums为例,判断条件为 i>0 && nums[i]=nums[i-1] && !vis[i-1] 。
class Solution {
public:vector<vector<int>> vv;vector<int> v;vector<int> cpnums;bool vis[10]={false};int n;vector<vector<int>> permuteUnique(vector<int>& nums) {cpnums=nums;n=cpnums.size();sort(cpnums.begin(),cpnums.end());helper(0);return vv;}void helper(int pos){if(pos==n){vv.push_back(v);return;}for(int i=0;i<n;i++){if(!vis[i]){if(i>0 && cpnums[i]==cpnums[i-1] && !vis[i-1]) continue;v.push_back(cpnums[i]);vis[i]=true;helper(pos+1);vis[i]=false;v.pop_back();}}}
};方法二
class Solution {
public:vector<vector<int>> vv;int n;vector<int> cpnums;bool vis[10];vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());cpnums=nums;n=cpnums.size();helper(0);return vv;}void helper(int pos){if(pos==n){vector<int> v;for(int x:cpnums)v.push_back(x);vv.push_back(v);return;}else{set<int> st;for(int i=pos;i<n;i++){if(!st.count(cpnums[i])){st.emplace(cpnums[i]);Swap(&cpnums[pos],&cpnums[i]);helper(pos+1);Swap(&cpnums[pos],&cpnums[i]);}}}}void Swap(int* a,int* b){int tmp=*a;*a=*b;*b=tmp;}
};该方法不同于方法一,除了是通过交换不同位置的元素之外,在解决重复元素会出现相同全排列问题上,使用set将已访问的元素进行统计,当与要访问的元素相等的元素已经被访问过,那么访问该元素没问题,但是与要访问的元素相等的元素没有被访问过,那么就会出现相同的全排列,因此这一点就是突破口,其实思想还是和方法一解决的突破点一样。
用回溯法解决其它类型的问题
生成匹配的括号
题目

分析
如果输入n,那么生成的括号组合包含n个左括号和n个右括号。因此生成这样的组合需要2n步,每一步生成一个括号,每一步都面临两个选项,既可能生成左括号又可能生成右括号。由此看来,这个问题很适合用回溯法解决。
在生成括号组合时需要注意每一步都要满足限制条件。第一个限制条件是左括号或右括号的树木不能唱过n个。第二个限制条件是括号的匹配原则,即在任意步骤中已经生成的右括号的数目不能唱过左括号的数目。
代码
class Solution {
public:vector<string> v;string s;vector<string> generateParenthesis(int n) {helper(n,n);return v;}void helper(int left,int right){if(left==0 && right==0){v.push_back(s);return;}if(left>0){s+='(';helper(left-1,right);s.pop_back();}if(right>left){s+=')';helper(left,right-1);s.pop_back();}}
};分割回文子字符串
题目

分析
当处理到字符创中的某个字符时,如果包括该字符在内后面还有n个字符,那么此时面临n个选项,即分割出长度为1的子字符串(只包含该字符),分割出长度为2的子字符串,以此类推,分割出长度为n的子字符串由于题目要求分割出来的每个子字符串都是回文的,因此需要逐一判断这n个子字符串是不是回文的,只有回文子字符串才是符合条件的分割,分割出一段回文子字符串之后,接着分割后面的字符串。
代码
class Solution {
public:vector<vector<string>> ans;vector<string> v;string cps;int n;vector<vector<string>> partition(string s) {cps=s;n=cps.size();helper(0);return ans;}void helper(int start){if(start==n){ans.push_back(v);return;}for(int i=start;i<n;i++){if(isPalindrome(start,i)){v.push_back(cps.substr(start,i-start+1));helper(i+1);v.pop_back();}}}bool isPalindrome(int begin,int end){while(begin<end){if(cps[begin++]!=cps[end--])return false;}return true;}
};恢复IP地址
题目


分析
IP地址的特点:一个IP被3个 '.' 字符分割成4段,每段都是从0到255之间的一个数字,另外,除“0”本身外,其他数字不能以‘0’开头。
如果输入的字符串长度为n,由于逐一处理字符串中的每个字符,因此需要n步,并且每一步都面临两个可能的选项,由此可见,适合用回溯法来解决。
代码
class Solution {
public:bool isValidSeg(string seg){return (stoi(seg) <=255) && (seg == "0" || seg[0] !='0');}void helper(string s,int i,int segI,string seg,string ip,vector<string>& result){if(i==s.length() && segI == 3 && isValidSeg(seg))result.push_back(ip+seg);else if(i<s.length() && segI <=3){char ch=s[i];if(isValidSeg(seg+ch))helper(s,i+1,segI,seg+ch,ip,result);if(seg.length()>0 && segI<3)helper(s,i+1,segI+1,string(1,ch),ip+seg+".",result);}}vector<string> restoreIpAddresses(string s) {vector<string> result;helper(s,0,0,"","",result);return result;}
};总结
如果解决一个问题需要若干步骤,并且在每一步都面临若干选项,那么可以尝试用回溯法解决这个问题。适合用回溯法解决的问题的一个特点是解决这个问题存在多个解,而题目往往要求列出所有的解。
采用回溯法能够解决集合的排列,组合的很多问题,仔细分析这些问题及变种的代码就会发现最终的代码都大同小异,都可以采用递归来实现。递归代码需要先确定递归退出的边界条件,然后逐个处理集合中的元素。对于组合类问题,每个数字都面临两个选项,即添加当前数字到组合中或不添加当前数字到组合中。对于排列问题,一个数字如果后面有n个数字,那么面临n+1个选择,即可以将该数字和它后面的数字(包括它本身)交换。根据这些选项做出选择之后再调用递归函数处理后面的数字。
相关文章:

回溯大法总结
前言 本篇博客将分两步来进行,首先谈谈我对回溯法的理解,然后通过若干道题来进行讲解,最后总结 对回溯法的理解 回溯法可以看做蛮力法的升级版,它在解决问题时的每一步都尝试所有可能的选项,最终找出所以可行的方案…...

基于Android Studio图书管理,图书借阅系统
目录 项目介绍 图片展示 运行环境 获取方式 项目介绍 用户 书架:搜索书籍,查看书籍,借阅书籍,收藏书籍,借阅书籍必须在一个月之内还书; 我的:可以修改密码,退出登录ÿ…...

SCSS 基本使用详解
一、引言 SCSS 是 Sass(Syntactically Awesome Stylesheets)的其中一种语法,是一种预处理器脚本语言,能够扩展 CSS 的功能,使其更加强大和高效。SCSS 保留了 CSS 的原有语法,同时增加了变量、嵌套规则、混…...
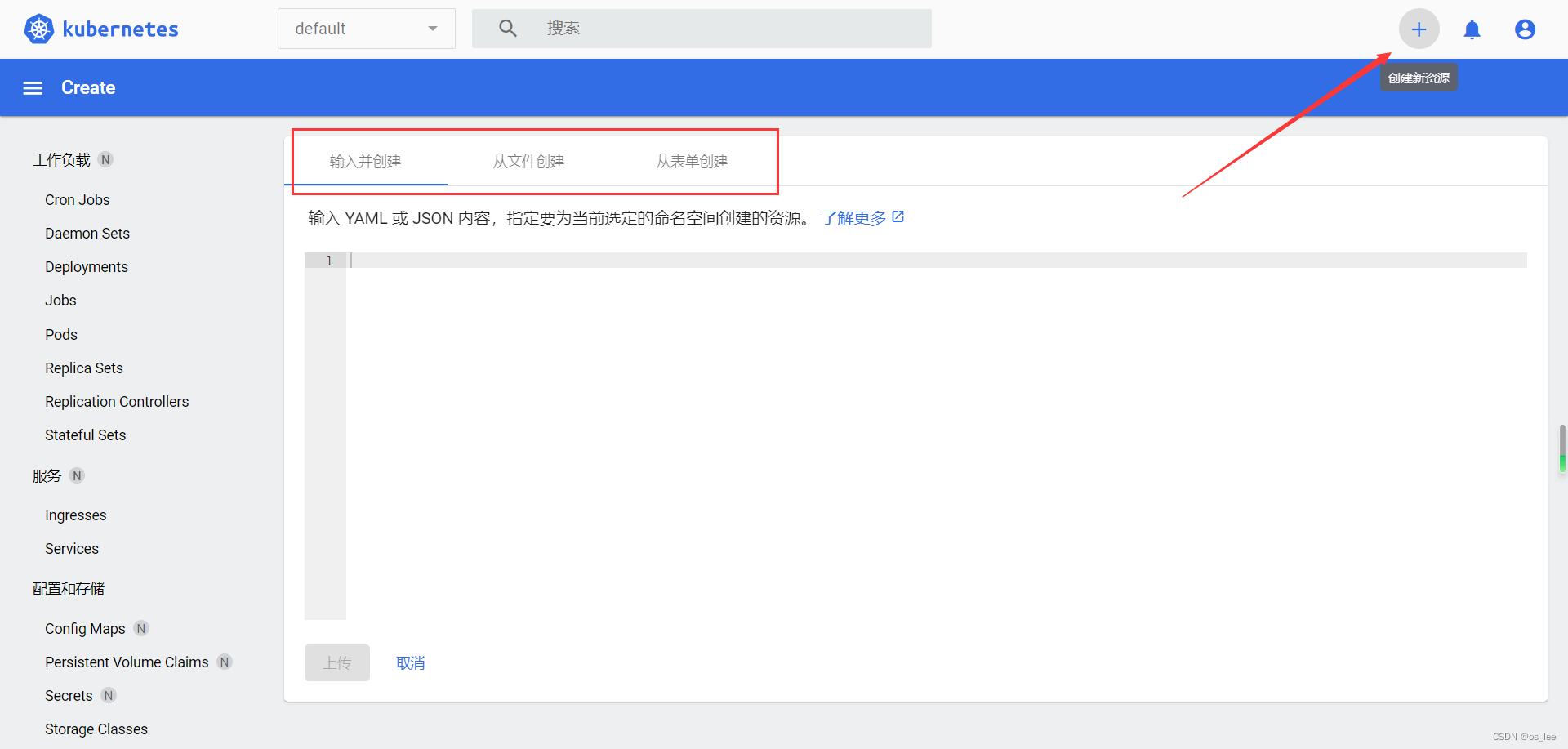
10.3.k8s的附加组件-图形化管理工具dashboard
目录 一、dashboard介绍 二、部署安装dashboard组件 1.下载dashboard本地文件 2.修改nodeport的端口范围 3.创建和查看dashboard 4.电脑浏览器访问测试 5.token登录方式登录dashboard 5.1.查看dashboard的token 5.2.继续查看用户token的secrets资源详细信息 5.3.复制…...
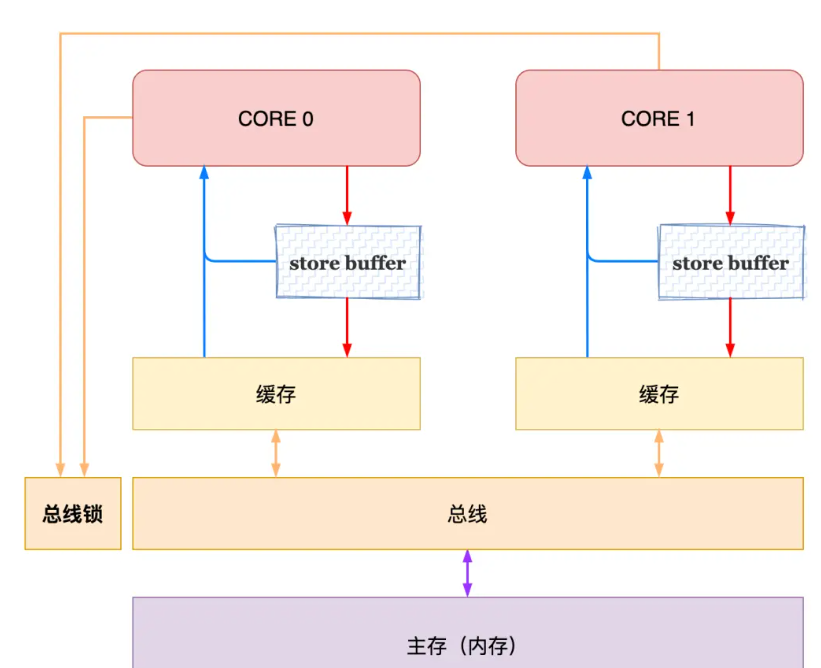
深入理解CPU缓存一致性
存储体系结构 速度快的存储硬件成本高、容量小,速度慢的成本低、容量大。为了权衡成本和速度,计算机存储分了很多层次,有寄存器、L1 cache、L2 cache、L3 cache、主存(内存)和硬盘等。 根据程序的空间局部性和时间局…...

python获取安装路径盘符
文章目录 一、前言二、实现方法一、前言 python写的客户端工具需要安装时,可以给用户一个默认的安装路径,如果直接写死个D、E、F盘什么的,那用户可能没有那个盘符,但是如果直接指定系统盘C盘,又不是那么友好,所以默认指定的安装路径应该尽量满足下面的要求: 盘符存在盘…...

CentOS 7.9安装NVIDIA P40显卡驱动、CUDA和cuDNN
文章目录 1、安装P40显卡驱动1.1 查看机器上有哪些显卡1.2 禁用nouveau1.3 安装依赖1.4 安装驱动 2、安装CUDA2.1 安装2.2 测试是否安装成功 3、安装cuDNN3.1 安装3.2 测试是否安装成功 4、总结 1、安装P40显卡驱动 1.1 查看机器上有哪些显卡 lspci | grep -i vga lspci | gr…...

SpringBoot多数据源启动出现循环依赖问题
在使用SpringBoot的项目中,如果是有使用多数据源,可能会存在启动时数据源循环依赖的报错,是因为使用了多数据源注入,和DataSourceAutoConfiguration数据源自动配置的DataSourceInitializerInvoker互相产生循环依赖导致。 这种错误…...
【一步一步了解Java系列】:何为数组,何为引用类型
看到这句话的时候证明:此刻你我都在努力加油陌生人个人主页:Gu Gu Study专栏:一步一步了解Java 喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹 喜欢的话可以点个赞谢谢了。 数组 数组是一推相同数据…...
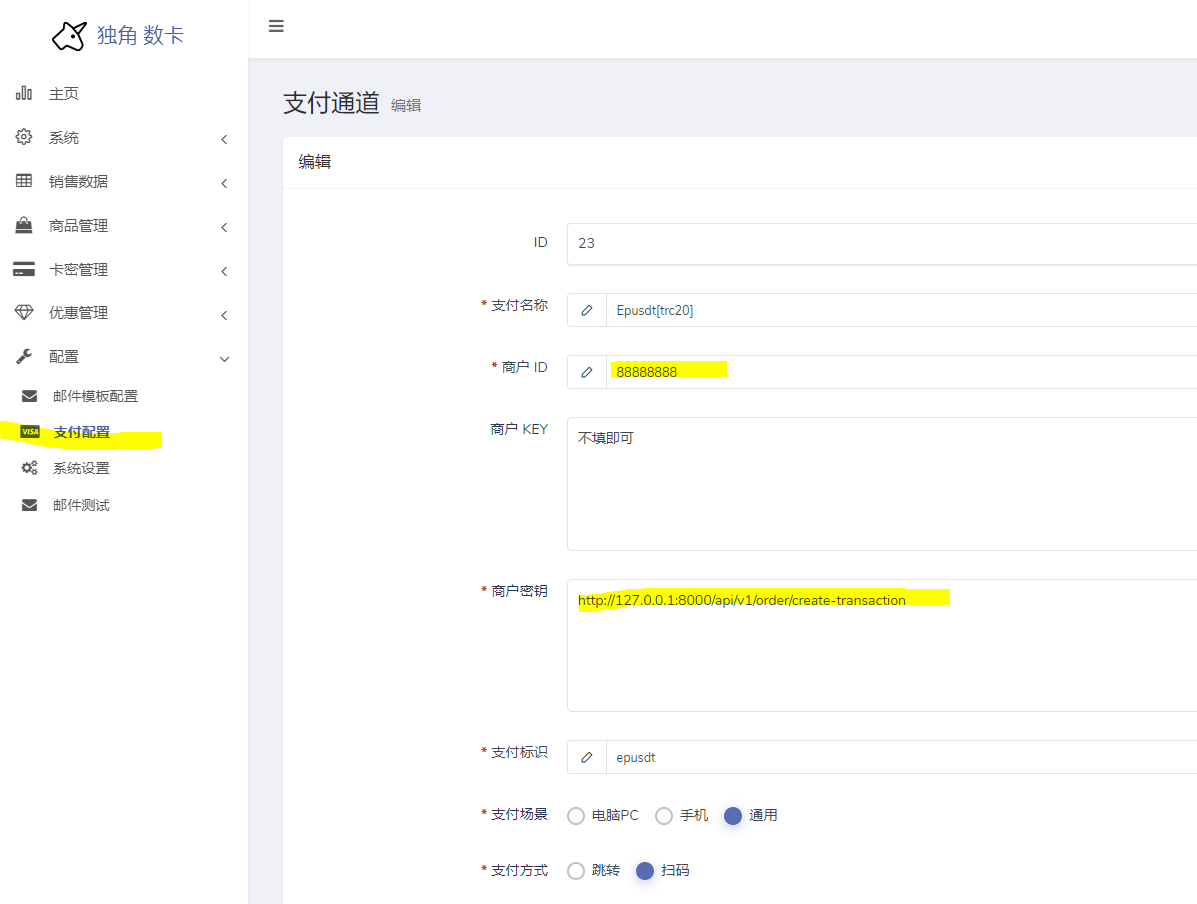
2024年5月份最新独角数卡使用USDT详细小白教程
直观配套视频教程 2024年5月份最新独角数卡安装及USDT使用详细小白教程 1、创建服务器 Centos或者Ubuntu2、宝塔面板开心版安装寶塔 Linux 面版 8.0.5 開心版 - 2024年1月12日 - 开心专区 - 异次元 - Powered by Discuz!Centos安装命令(默认安装是 8.0.1 直接在线升…...

【idea】idea2024最新版本下载_安装_破解
1、下载 下载地址:下载 IntelliJ IDEA – 领先的 Java 和 Kotlin IDE 下载完成: idea破解脚本下载链接:https://pan.baidu.com/s/1L5qq26cRABw8XuEn_CngKQ 提取码:6666 下载完成: 2、安装 1、双击idea的安装包&…...
部署CNI网络组件+k8s多master集群部署+负载均衡
一、环境部署 主机服务 192.168.91.5 K8S集群master01192.168.91.8 K8S集群master02192.168.91.6K8S集群node01192.168.91.7K8S集群node02192.168.91.9 负载均衡nginxkeepalive01(master)192.168.91.10 负载均衡nginxkeepalive02(backup&am…...
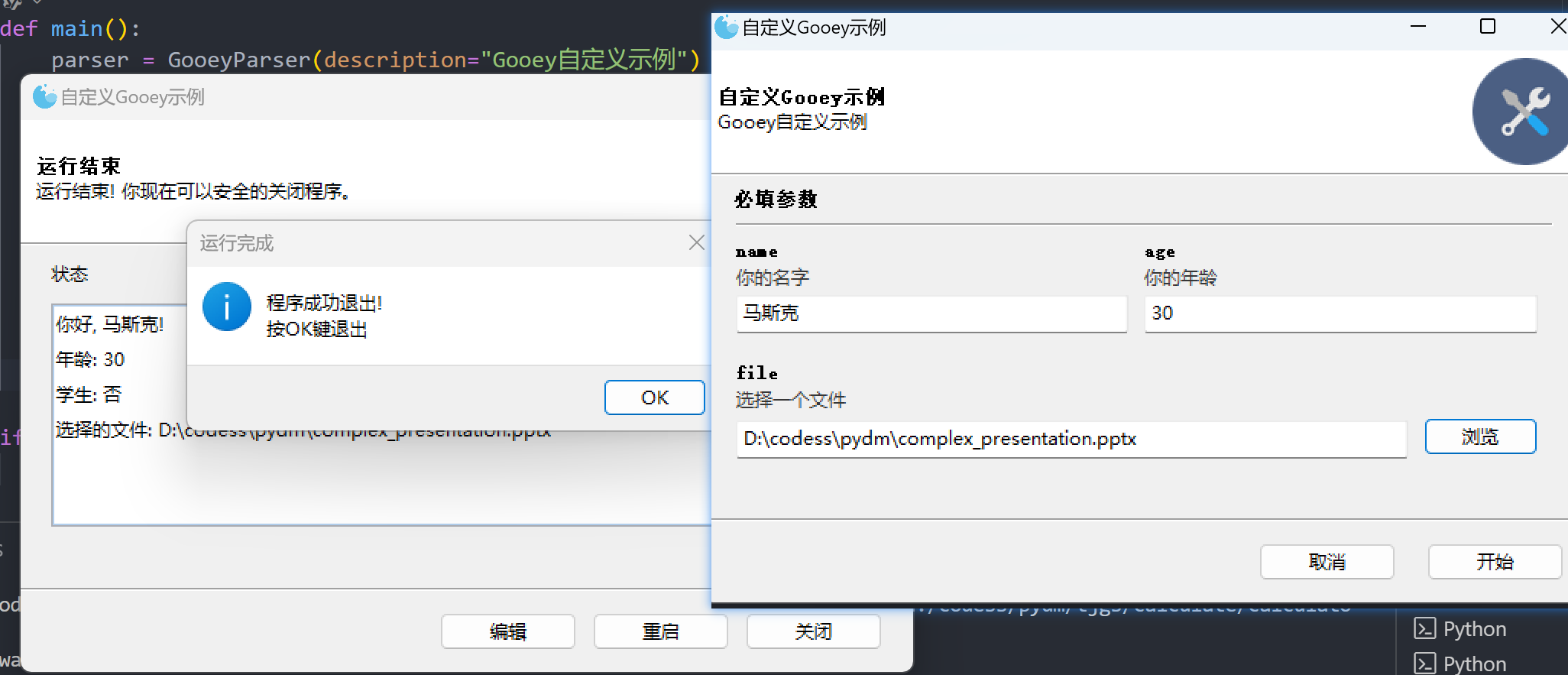
一个和蔼可亲的Python库,用Gooey为你的程序添加GUI
大家好,你有没有遇到过这样的情况:你写了一个非常棒的命令行程序,但当你分享给朋友或同事时,他们却因为害怕命令行而不愿意使用?这时候,一个简洁美观的图形用户界面(GUI)就派上用场了…...
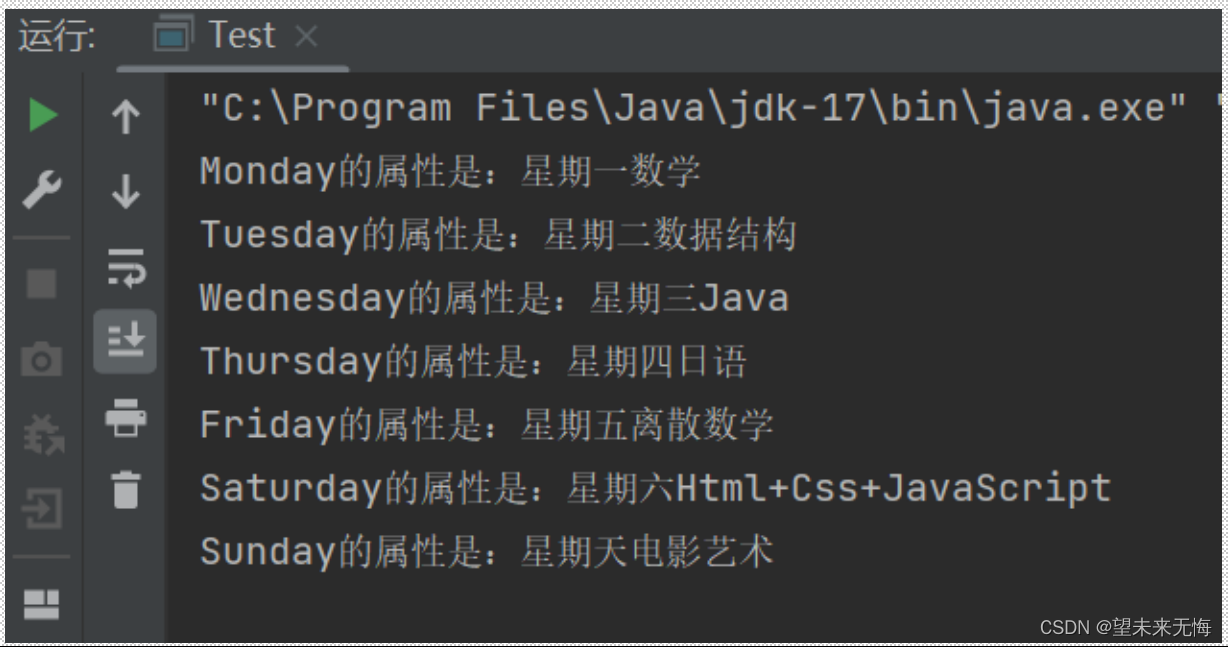
java抽象类,接口,枚举练习题
第一题: 答案: class Animal{//成员变量protected String name;protected int weight;//构造方法public Animal(){this.name"refer";this.weight50;}public Animal(String name,int weight){this.namename;this.weightweight;}//成员方法publ…...

探索Python技巧:零基础学习缩进与逻辑关系
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、理解Python的缩进语法 缩进规则详解 二、缩进在逻辑关系中的应用 逻辑块示例 三、实…...

【设计模式】JAVA Design Patterns——Callback(回调模式)
🔍目的 回调是一部分被当为参数来传递给其他代码的可执行代码,接收方的代码可以在一些方便的时候来调用它。 🔍解释 真实世界例子 我们需要被通知当执行的任务结束时。我们为调用者传递一个回调方法然后等它调用通知我们。 通俗描述 回调是一…...

Pandas高效数据清洗与转换技巧指南【数据预处理】
三、数据处理 1.合并数据(join、merge、concat函数,append函数) Concat()函数使用 1.concat操作可以将两个pandas表在垂直方向上进行粘合或者堆叠。 join属性为outer,或默认时,返回列名并集,如ÿ…...

kafka防止消息丢失配置
无消息丢失最佳实践配置: 不要使用 producer.send(msg),而要使用 producer.send(msg, callback) API。设置 acks all。是 Producer 参数。设置成 all,表明所有副本 Broker 都要接收到消息,g该消息才算是“已提交”。设置 retrie…...

Socket CAN中ctrlmode有哪些?
在Linux中,socketcan 的 ctrlmode 是一个用于配置CAN设备控制模式的标志字段。该字段的值由一组标志位组成,这些标志位控制CAN设备的各种操作模式。以下是一些常见的 ctrlmode 标志及其含义: CAN_CTRLMODE_LOOPBACK: 描述:启用回环模式。作用:设备在发送帧的同时会接收它…...
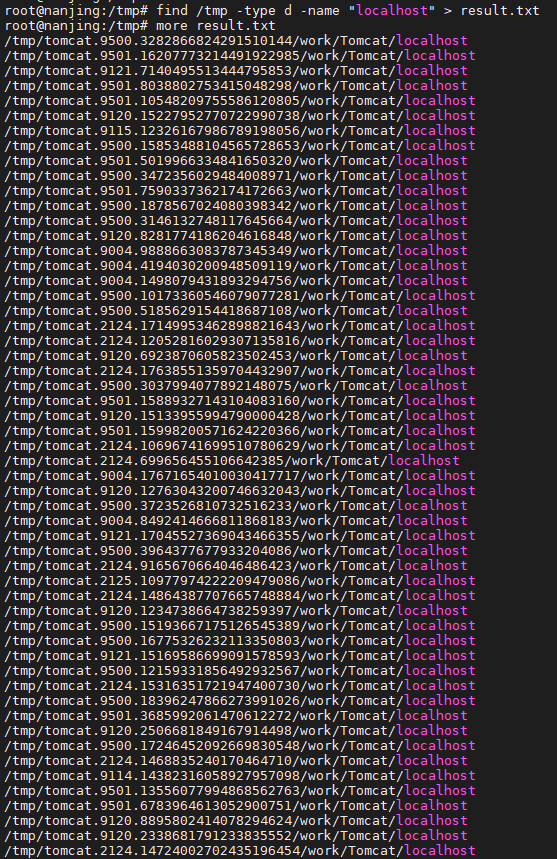
find 几招在 Linux 中高效地查找目录
1. 介绍 在 Linux 操作系统中,查找目录是一项常见的任务。无论是系统管理员还是普通用户,都可能需要查找特定的目录以执行各种操作,如导航文件系统、备份数据、删除文件等。Linux 提供了多种命令和工具来帮助我们在文件系统中快速找到目标目…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
