碌时刻必备!微信自动回复让你告别消息堆积
在忙碌的时候,我们往往会面临消息堆积如山的情况。无法及时回复消息不仅容易造成交流障碍,还可能错过重要的机会。
但是现在,有一个神奇的工具——个微管理系统,可以帮助我们轻松应对这个问题 ,实现微信自动回复。
首先,这个工具可以帮助你自动通过好友请求。当你在忙碌的时候,没有时间一个个手动确认每个好友请求,这个工具就会自动帮你通过这些好友请求,节省了大量的时间和精力。

其次,当有新的好友请求通过后,这个工具还能自动回复消息,比如欢迎消息、产品介绍等。帮助你即时问候新加的好友,让新朋友感受到你的热情和专业。

同时,你还可以设置关键字自动回复。这意味着,当有人发送含有设置的关键字的消息时,这个工具会根据你事先设定的回复内容对其进行回复。让你可以更加智能地处理各类相似问题,提高沟通效率。
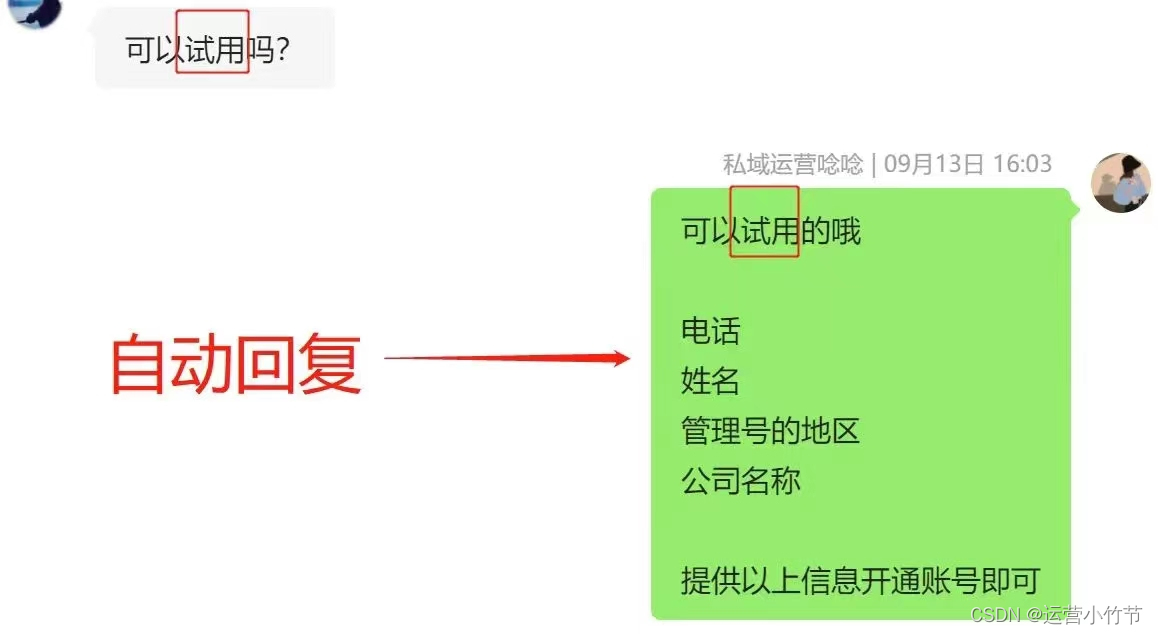
除了自动回复,你还可以在个微管理系统中进行批量自动加好友、批量群发、朋友圈统一管理等操作,这些功能的存在,极大地提高了我们的工作效率和运营效果。
如果你也想告别消息堆积,不妨尝试一下哦!今天的分享到这里就结束啦,咱们下期再见!
点击免费试用私域管理系统
相关文章:

碌时刻必备!微信自动回复让你告别消息堆积
在忙碌的时候,我们往往会面临消息堆积如山的情况。无法及时回复消息不仅容易造成交流障碍,还可能错过重要的机会。 但是现在,有一个神奇的工具——个微管理系统,可以帮助我们轻松应对这个问题 ,实现微信自动回复。 首…...
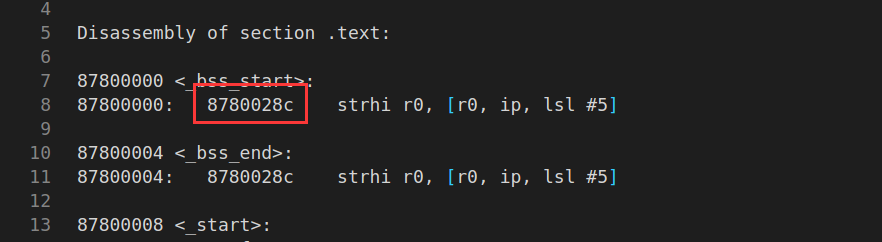
【ARM 裸机】按键输入
本节学习按键输入,先拷贝上一节工程文件, 1、驱动编写 新建 key 的 .h 和 .c 文件; 再查看一下硬件原理图如下; 由此可知,KEY0 按键接在 UART1_CTS 引脚上,默认情况下为高电平,按键按下为…...

站在ESG“20+”新起点上,看中国ESG先锋探索力量
全链减碳、建设绿色工厂、打造零碳产品、守护生物多样性、向受灾群众捐助……不知你是否察觉,自“双碳”目标提出以来,一股“可持续发展热潮”正覆盖各行各业,并且渗透到我们衣食住行的方方面面。在资本市场,ESG投资热潮更是席卷全…...

【CTF Web】CTFShow web4 Writeup(SQL注入+PHP+字符型注入)
web4 1 管理员阿呆又失败了,这次一定要堵住漏洞 解法 注意到: <!-- flag in id 1000 -->拦截很多种字符,连 select 也不给用了。 if(preg_match("/or|\-|\\\|\/|\\*|\<|\>|\!|x|hex|\(|\)|\|select/i",$id)){die(&q…...
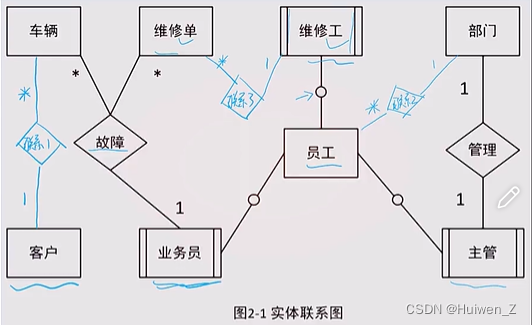
软件设计师备考 | 案例专题之数据库设计 概念与例题
相关概念 关注上图中的两个部分: 概念结构设计 设计E-R图,也即实体-联系图。 工作步骤:选择局部应用、逐一设计分E-R图、E-R图合并。进行合并时,它们之间存在的冲突主要有以下3类: 属性冲突。同一属性可能会存在于…...
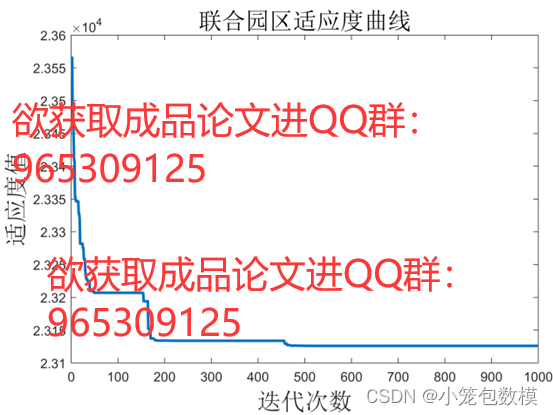
【全网最全】2024电工杯数学建模A题成品论文+前三题完整解答matlab+py代码等(后续会更新成品论文)
您的点赞收藏是我继续更新的最大动力! 一定要点击如下的卡片链接,那是获取资料的入口! 【全网最全】2024电工杯数学建模A题成品论文前三题完整解答matlabpy代码等(后续会更新成品论文)「首先来看看目前已有的资料&am…...

基于.net开发的博客系统
基于.net开发可以批量上传md文件生成文章的博客系统 .NET 个人博客 基于.net开发的博客系统 个人博客系统,采用.net core微服务技术搭建,采用传统的MVC模式,使用EF core来对mysql数据库(sqlite数据库)进行CRUD操作项目 为什么要自己开发博客…...

python给图片加上图片水印
python给图片加上图片水印 作用效果代码 作用 给图片加上图片水印图片水印的透明度,位置可自定义 效果 原始图片: 水印图片: 添加水印后的图片: 代码 from PIL import Image, ImageDraw, ImageFontdef add_watermark(in…...

Redis实现MQ
MQ的提出 上游发出请求后阻塞等待下游给到反馈,否则整个流程将一直阻塞。 提出mq之后:即有producer mq consumer 三者 MQ的特点 异步解耦 在有了 mq 后,producer 不需要过分关心 consumer 的身份信息,只需要把消息按照指定的协议…...

【Linux】进程终止与进程等待
目录 进程终止 errno exit和_exit 进程等待 wait和waitpid 宏:WIFEXITED 非阻塞等待 进程终止 下面要谈的一个话题就是进程终止,就是说一个进程退出了,可能有三种情况 1.进程代码执行完,结果是正确的 2.进程代码执行完&…...

数据结构_链式二叉树(Chained binary tree)基础
✨✨所属专栏:数据结构✨✨ ✨✨作者主页:嶔某✨✨ 二叉树的遍历 前序、中序以及后序遍历 学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的结点进行相应的操作ÿ…...

python梯度下降法求解三元线性回归系数,并绘制结果
import numpy as np import matplotlib.pyplot as plt # 生成随机数据 np.random.seed(0) X1 2 * np.random.rand(100, 1) X2 3 * np.random.rand(100, 1) X3 4 * np.random.rand(100, 1) y 4 3 * X1 5 * X2 2 * X3 np.random.randn(100, 1) # 合并特征 X_b np.hsta…...

Linux基础(五):常用基本命令
从本节开始,我们正式进入Linux的学习,通过前面的了解,我们知道我们要以命令的形式使用操作系统(使用操作系统提供的各类命令,以获得字符反馈的形式去使用操作系统。),因此,我们是很有…...

原始字面常量(C++11)
原始字面常量(C11) 文章目录 原始字面常量(C11)前言一、原始字面量二、代码示例总结 前言 字面量一般是指数值(12、454等)和字符串(“Hw”、“h\t”),但是有时候我们想表…...
|设计模式的六大原则)
C++|设计模式(〇)|设计模式的六大原则
这里文章只做简要描述,作为扫盲 在软件开发过程中,遵循一定的设计原则可以帮助开发者创建更加灵活、可维护和可扩展的系统。设计模式的六大原则是面向对象设计的核心理念,本文将详细介绍这些原则,并结合实例说明它们的重要性和应用…...
【排序算法】——归并排序(递归与非递归)含动图
制作不易,三连支持一下吧!!! 文章目录 前言一.归并排序递归方法实现二.归并排序非递归方法实现 前言 这篇博客我们将介绍归并排序的原理和实现过程。 一、归并排序递归方法实现 基本思想: 归并排序(MERGE-…...

Mysql自增id、uuid、雪花算法id的比较
MySQL自增id: 优点: 1.简单易用 MySQL自增id 由数据库自动生成。 2.效率高 自增id是按顺序递增的,可以提高插入和查询的效率。 3.索引效率高 自增id可以作为主键或索引列,提高查询效率。 缺点: 1.不适用于分布式系统 在分布式…...

【会议征稿,IEEE出版】第九届信息科学、计算机技术与交通运输国际学术会议(ISCTT 2024,6月28-30)
第九届信息科学、计算机技术与交通运输国际学术会议(ISCTT 2024)将于2024年6月28-30日在中国绵阳举行。 ISCTT 2024将围绕 “信息科学”、"计算机技术”、“交通运输” 等最新研究领域,为来自国内外高等院校、科学研究所、企事业单位的专…...

二十八篇:嵌入式系统实战指南:案例研究与未来挑战
嵌入式系统实战指南:案例研究与未来挑战 1. 引言 1.1 嵌入式系统的重要性及其应用广度 在当今快速发展的技术领域中,嵌入式系统扮演着至关重要的角色。这些系统是专门设计的计算机硬件和软件的组合,旨在执行特定任务,如控制、监…...

探索编程乐趣:绘制螺旋图的奇幻之旅
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言:编程的魔法世界 二、绘制螺旋图的准备工作 三、代码实战:…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
