【C++】详解AVL树——平衡二叉搜索树
个人主页:东洛的克莱斯韦克-CSDN博客
祝福语:愿你拥抱自由的风
目录
二叉搜索树
AVL树概述
平衡因子
旋转情况分类
左单旋
右单旋
左右双旋
右左双旋
AVL树节点设计
AVL树设计
详解单旋
左单旋
右单旋
详解双旋
左右双旋
平衡因子情况如下
右左双旋
平衡因子情况如下
二叉搜索树
【C++】详解二叉搜索树-CSDN博客
AVL树概述
平衡树:左子树的高度等于右子树的高度
不平衡树:左子树的高度不等于等于右子树的高度
二叉搜索树很难是一颗平衡树。
对二叉树进行插入和删除的操作,或插入大量的数据不够随机,都会是使二叉搜索树不够平衡。
极端情况下,二叉树会退化成类似链表的结构,那么二叉搜索树查询数据的效率荡然无存。
在二叉树的基础上加入平衡的概念就是平衡二叉搜索树,也叫AVL树。
AVL树也不是一颗绝对的平衡树,AVL树的平衡是相对的,它允许左子树和右子树的高度为 1 ,但不能超过 1 。
平衡是相对的很好理解,因为一个父亲节点最多只能有两个孩子节点,而数据又是一个一个插入的,所以一定会出现左子树和右子树高度差为 1 的情况。
B树可达到绝对平衡,因为B树是多叉结构——一个父亲节点有多个孩子节点
如果左子树和右子树的高度差为 2 ,就视为打破平衡。
如果打破平衡,就需要通过旋转这一操作让左右子树的高度差小于等于 1 。
AVL树是保持一种相对平衡的状态,而不是绝对平衡。那么AVL树搜索数据的效率只能是接近。
AVL树只是保证了搜索效率的下限,而不是提高了上限
平衡因子
平衡因子这一概念并不是AVL树所必备的——从代码实现的角度来说,如果不加入平衡因子的概念理解起来会比较抽象。
平衡因子:让每个节点存一个整型,该整形值的大小等于右子树的高度减左子树的高度
平衡因子等于 0 :左右子树平衡
平衡因子等于 1 :左右子树相对平衡,右树偏高
平衡因子等于 -1 :左右子树相对平衡,左树树偏高
平衡因子等于 2 或 -2 :左右子树不平衡
平衡因子的更新:
插入父亲节点的右边平衡因子加加,插入父亲节点的右边平衡因子减减,
父亲节点更新后的平衡因子等于 1 或 -1 ,需要不断往上(溯源)更新,直到父亲节点的平衡因子为 0 或 更新至整棵树的根节点就停止更新。
如果父亲节点的平衡因子为 2 或 -2 时,需要对这棵子树旋转,旋转后更新平衡因子
示例
旋转情况分类
旋转分为:
左单旋 右单旋 左右双旋 右左双旋
左单旋
:新节点插入较高右子树的右侧
具象图:

抽象图:

那么左单旋是怎么旋的呢?核心步骤为:
设父亲节点为:fathernode 孩子节点为:cur
让cur的左孩子成为fathernode的右孩子,
再让fathernode成为cur的左孩子。
如下示意图

右单旋
:新节点插入较高左子树的左侧
具象图:

抽象图:

那么右单旋是怎么旋的呢?核心步骤为:
设父亲节点为:fathernode 孩子节点为:cur
让cur的右孩子成为fathernode的左孩子,
再让fathernode成为cur的右孩子
如下示意图:

左右双旋
:新节点插入在较高左子树的右侧——先左单旋再右单旋
左右双旋的核心步骤为:
设父亲节点为:fathernode
父亲的左孩子节点为:fathernodeL
父亲的左孩子节点的右孩子节点的为fathernodeLR
先让fathernodeL左单旋,再让fathernodeLR进行右单旋
这里小编直接上抽象图:

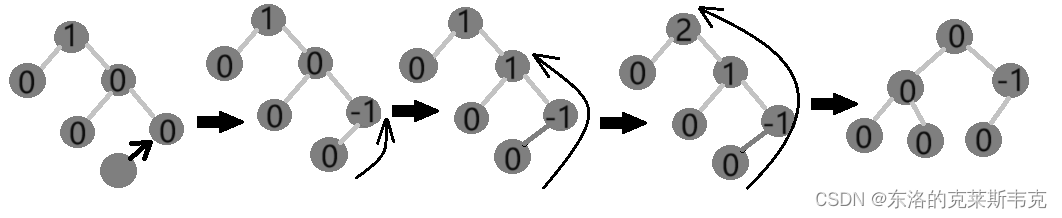
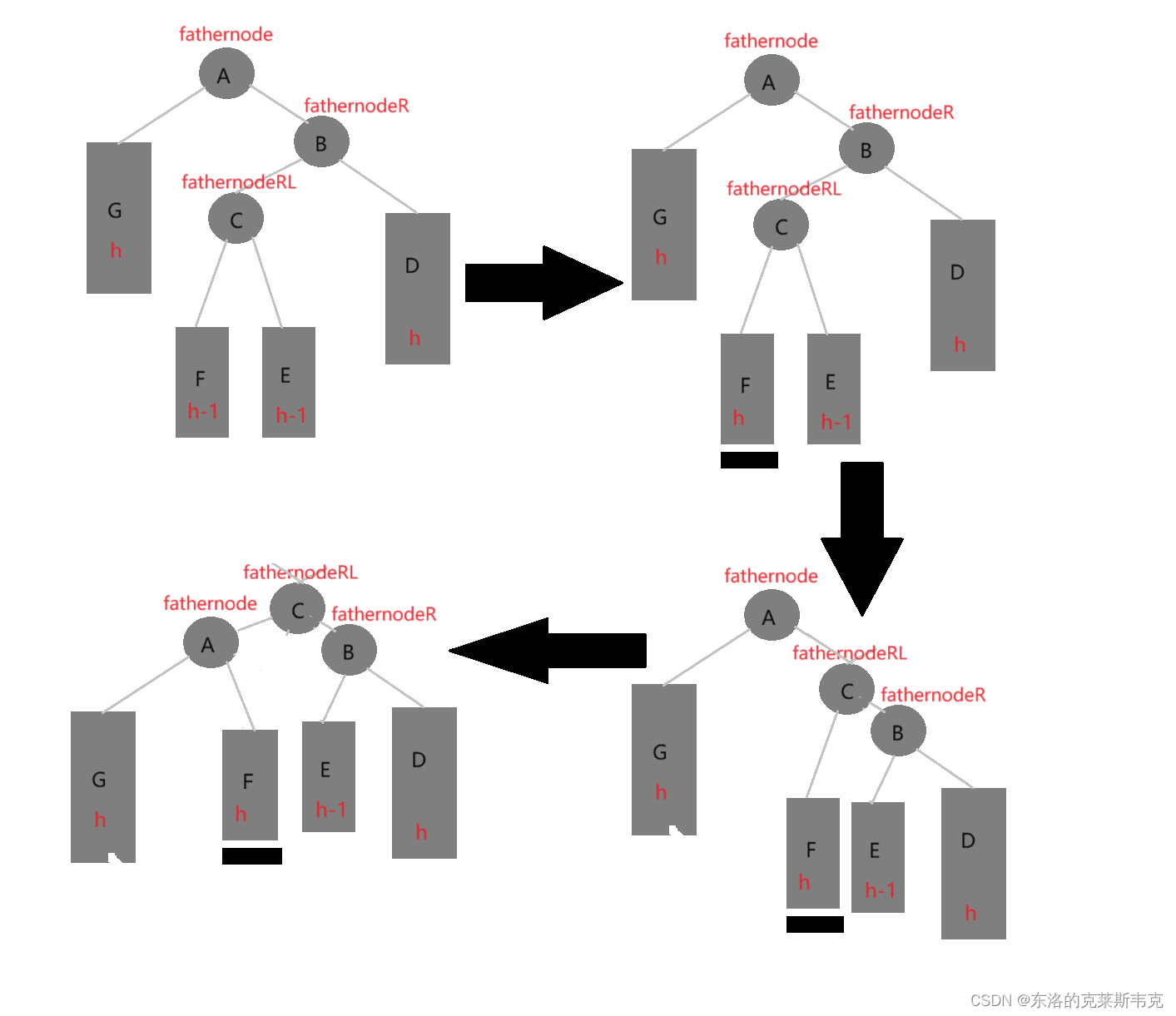
右左双旋
:新节点插入再较高右子树的左侧——先右单旋再左单旋
设父亲节点为:fathernode
父亲的 右孩子节点为:fathernodeR
父亲的右孩子节点的左孩子节点的为fathernodeRL
先对fathernodeR进行右单旋,再对fathernode进行左单旋。
示意图:
AVL树节点设计
【C++】详解C++的模板-CSDN博客
AVL树的节点需要三个指针,分别指向左孩子节点,右孩子节点,父亲节点。指向父亲节点的指针是为了能溯源更新平衡因子。
需要一个整型存储平衡因子,平衡因子在构造函数的初始化列表中初始化为 0,因为新节点左右孩子都为空。
template <class K>
class AVLTreeNode
{
public:AVLTreeNode(const K& key) //构造函数:_key(key), _left(nullptr), _right(nullptr), _FatherNode(nullptr), _bf(0){}K _key; //键值 AVLTreeNode<K>* _left;//左孩子AVLTreeNode<K>* _right;//右孩子AVLTreeNode<K>* _FatherNode;//父亲 int _bf;//平衡因子};AVL树设计
template <class K>
class AVLTree
{typedef AVLTreeNode<K> node; node* _root;public:AVLTree() //构造函数,初始化为空树:_root(nullptr){}bool Insert(const K& key)//插入元素{
//if (nullptr == _root) //是否是空树{_root = new node(key); return true;}
//node* cur = _root;node* fathernode = nullptr;while (cur) //查找插入的位置,如果树中已经有要插入的值,则插入失败,{if (cur->_key < key){fathernode = cur;cur = cur->_right;}else if (cur->_key > key){fathernode = cur;cur = cur->_left;}else{return false;}}cur = new node(key); //新插入节点 if (fathernode->_key < cur->_key) //判断新节点应该是左孩子还是右孩子{fathernode->_right = cur;cur->_FatherNode = fathernode;}else{fathernode->_left = cur;cur->_FatherNode = fathernode;}//while (fathernode)//更新平衡因子{if (cur == fathernode->_left){fathernode->_bf--;}else if (cur == fathernode->_right){fathernode->_bf++;}//if (fathernode->_bf == 0){// 更新结束break;}else if (fathernode->_bf == 1 || fathernode->_bf == -1){// 继续往上更新cur = fathernode;fathernode = fathernode->_FatherNode;}else if (fathernode->_bf == 2 || fathernode->_bf == -2){// 子树不平衡了,需要旋转if (fathernode->_bf == 2 && cur->_bf == 1){RevolveLeft(fathernode);//左单旋}else if (fathernode->_bf == -2 && cur->_bf == -1){RevolveRight(fathernode);//右单旋}else if (fathernode->_bf == 2 && cur->_bf == -1){RevolveRightLeft(fathernode); //右左双旋 }else if (fathernode->_bf == -2 && cur->_bf == 1){RevolveLeftRight(fathernode);//左右双旋}else{assert(false); //平衡因子出问题了}break;}}return true;}}下面通过代码的细节来深入理解旋转
详解单旋
左单旋
完整代码如下
void RevolveLeft(node *& fathernode)//左单旋
{node* cur = fathernode->_right; //父亲节点的右孩子fathernode->_right = cur->_left; //更改指向关系if (cur->_left != nullptr) //特殊情况cur->_left->_FatherNode = fathernode;//更改指向关系cur->_FatherNode = fathernode->_FatherNode;//更改指向关系if (fathernode->_FatherNode != nullptr) //为空是特殊情况,{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更改指向关系}else{fathernode->_FatherNode->_left = cur;//更改指向关系}}cur->_left = fathernode;//更改指向关系fathernode->_FatherNode = cur;//更改指向关系fathernode->_bf = 0; //更新平衡因子cur->_bf = 0;}处理指向关系时,一定不要忘了更改父亲的指向关系
经过左单旋之后,父亲节点和右孩子节点的平衡因子都为 0 ,可参考上文图示。
特殊情况如下,如果不处理特殊情况,程序很容易崩溃

右单旋
void RevolveRight(node *& fathernode) //右单旋
{node* cur = fathernode->_left; //父亲节点的左节点fathernode->_left = cur->_right;//更新指向关系if (cur->_right != nullptr) //特殊情况cur->_right->_FatherNode = fathernode;//更新指向关系cur->_FatherNode = fathernode->_FatherNode;//更新指向关系if (fathernode->_FatherNode != nullptr)//特殊情况{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更新指向关系}else{fathernode->_FatherNode->_left = cur;//更新指向关系}}cur->_right = fathernode;//更新指向关系fathernode->_FatherNode = cur;//更新指向关系fathernode->_bf = 0;//更新平衡因子cur->_bf = 0;
}详解双旋
左右双旋
左右双旋只需复用左单旋和右单旋即可,但平衡因子的更新却比较麻烦。
完整代码如下
void RevolveLeftRight(node *& fathernode)//左右双旋 {node* fathernodeL = fathernode->_left; //父亲节点的左孩子节点node* fathernodeLR = fathernodeL->_right;//父亲节点的左孩子节点的右孩子节点int bf = fathernodeLR->_bf; //保存平衡因子,实际是为了判断是插入了fathernodeLR左边还是右边还是fathernodeLR本身插入RevolveLeft(fathernodeL);RevolveRight(fathernode);//更新平衡因子if (bf == 0){fathernode->_bf = 0;fathernodeL->_bf = 0;fathernodeLR->_bf = 0;}else if (bf == -1){fathernode->_bf = 1;fathernodeL->_bf = 0;fathernodeLR->_bf = 0;}else if (bf == 1){fathernodeL->_bf = -1;fathernode = 0;fathernodeLR = 0;}else{assert(false);}}平衡因子情况如下

右左双旋
完整代码如下
void RevolveRightLeft(node *& fathernode) //右左双旋 {node* fathernodeR = fathernode->_right; node* fathernodeRL = fathernodeR->_left;int bf = fathernodeRL->_bf;RevolveRight(fathernodeR);RevolveLeft(fathernode);if (bf == 0){fathernode->_bf = 0;fathernodeR->_bf = 0;fathernodeRL->_bf = 0;}else if (bf == 1){fathernode->_bf = -1;fathernodeR->_bf = 0;fathernodeRL->_bf = 0;}else if (bf == -1){fathernodeR->_bf = 1;fathernode->_bf = 0;fathernodeRL->_bf = 0;}else{assert(false); }}平衡因子情况如下

相关文章:

【C++】详解AVL树——平衡二叉搜索树
个人主页:东洛的克莱斯韦克-CSDN博客 祝福语:愿你拥抱自由的风 目录 二叉搜索树 AVL树概述 平衡因子 旋转情况分类 左单旋 右单旋 左右双旋 右左双旋 AVL树节点设计 AVL树设计 详解单旋 左单旋 右单旋 详解双旋 左右双旋 平衡因子情况如…...
《计算机网络微课堂》2-2 物理层下面的传输媒体
请大家注意,传输媒体不属于计算机网络体系结构的任何一层,如果非要将它添加到体系结构中,那只能将其放在物理层之下。 传输媒体可分为两类:一类是导引型传输媒体,另一类是非导引型传输媒体。 在导引型传输媒体…...
【算法设计与分析】基于Go语言实现动态规划法解决TSP问题
本文针对于最近正在学习的Go语言,以及算法课实验所需内容进行Coding,一举两得! 一、前言 由于这个实验不要求向之前的实验一样做到那种连线的可视化,故可以用图形界面不那么好实现的语言进行编写,考虑到Go语言的…...
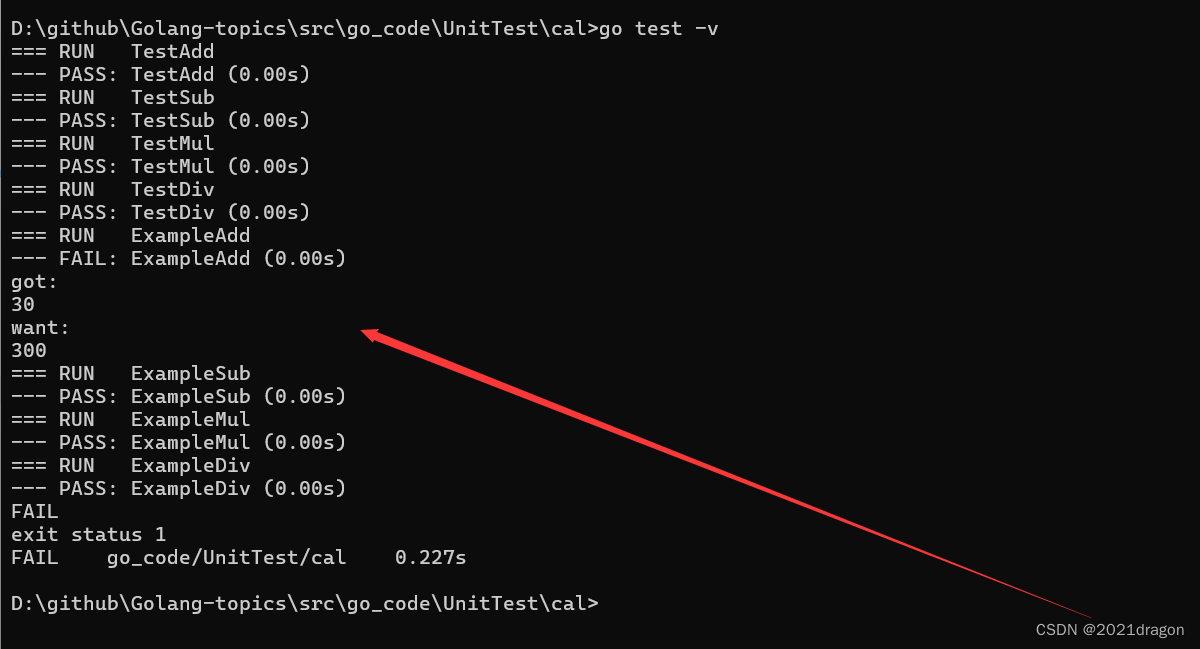
Golang单元测试
文章目录 传统测试方法基本介绍主要缺点 单元测试基本介绍测试函数基准测试示例函数 传统测试方法 基本介绍 基本介绍 代码测试是软件开发中的一项重要实践,用于验证代码的正确性、可靠性和预期行为。通过代码测试,开发者可以发现和修复潜在的错误、确保…...
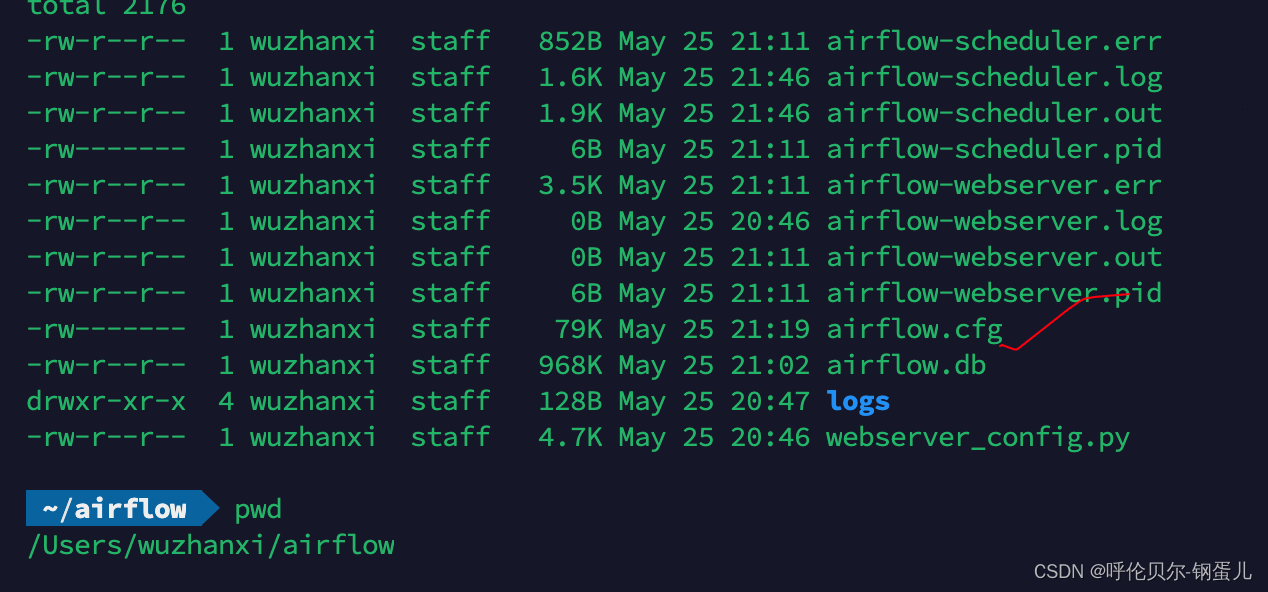
mac下安装airflow
背景:因为用的是Mac的M芯片的电脑,安装很多东西都经常报错,最近在研究怎么把大数据集群上的crontab下的任务都配置到一个可视化工具中,发现airflow好像是个不错的选择,然后就研究怎么先安装使用起来,后面再…...

二进制中1的个数c++
题目描述 计算鸭给定一个十进制非负整数 NN,求其对应 22 进制数中 11 的个数。 输入 输入包含一行,包含一个非负整数 NN。(N < 10^9) 输出 输出一行,包含一个整数,表示 NN 的 22 进制表示中 11 的个数。 样例输入 100 …...

【面试干货】数据库乐观锁,悲观锁的区别,怎么实现
【面试干货】数据库乐观锁,悲观锁的区别,怎么实现 1、乐观锁,悲观锁的区别2、总结 💖The Begin💖点点关注,收藏不迷路💖 1、乐观锁,悲观锁的区别 悲观锁(Pessimistic Lo…...
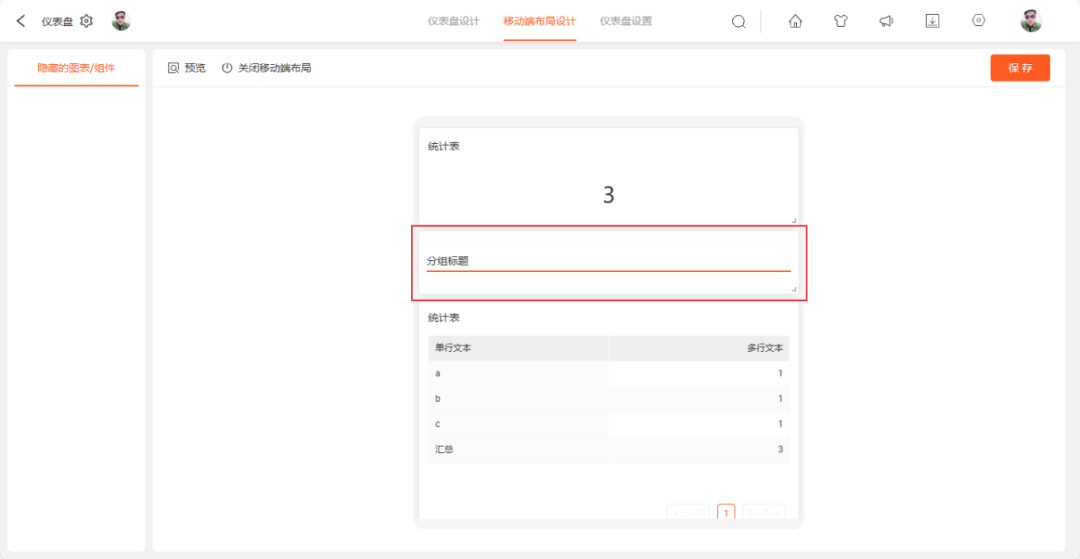
移动端仪表盘,支持更多组件
05/22 主要更新模块概览 定位函数 快捷筛选 轨迹图表 时间组件 01 表单管理 1.1 【表单组件】- 表单关联新增支持自定义按钮样式 说明: 表单关联-关联数据按钮,原仅支持默认按钮样式,现增加关联数据按钮自定义功能,满…...

科技产业园3D探秘:未来科技之城的奇幻之旅
在数字时代的浪潮中,科技产业园区成为了推动城市经济发展、科技创新的重要引擎。 当我们打开科技产业园的3D可视化模型,仿佛穿越时空,来到了一个充满奇幻色彩的科技世界。在这里,高楼大厦鳞次栉比,绿色植被点缀其间&am…...
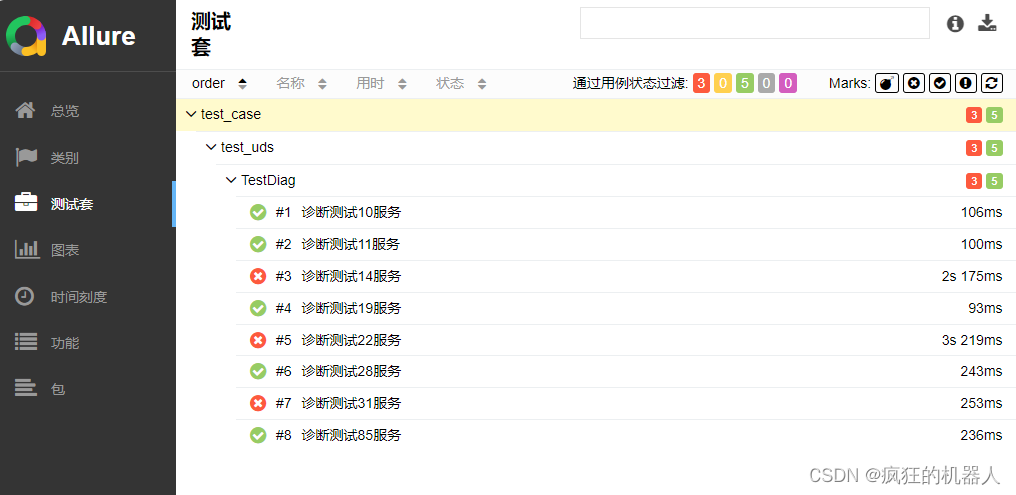
【Python搞定车载自动化测试】——Python基于Pytest框架实现UDS诊断自动化(含Python源码)
系列文章目录 【Python搞定车载自动化测试】系列文章目录汇总 文章目录 系列文章目录💯💯💯 前言💯💯💯一、环境搭建1.软件环境2.硬件环境 二、目录结构三、源码展示1.诊断基础函数方法2.诊断业务函数方法…...

探索SPI单线传输模式中时钟线与数据传输的简化
探索SPI单线传输模式:时钟线与数据传输的简化之道 在当今的嵌入式系统和微控制器通信中,串行外设接口(SPI)因其高速、全双工和同步的特点而广受欢迎。然而,随着设备尺寸和复杂性的不断减少,对SPI通信的简化…...

使用FFmpeg推流实现在B站24小时点歌直播
使用FFmpeg推流实现在B站24小时点歌直播 本文首发于个人博客 安装FFmpeg centos7 https://www.myfreax.com/how-to-install-ffmpeg-on-centos-7/ https://linuxize.com/post/how-to-install-ffmpeg-on-centos-7/ 使用FFmpeg在B站直播 https://zhuanlan.zhihu.com/p/2395…...

汽车防抱死制动系统ABS的单片机程序Proteus仿真设计
次设计对汽车防抱死系统进行简单的设计,针对车速、轮速两个信号进行分析,并根据最佳滑移率计算。采用对比实时滑移率对比分析,ECU控制制动器进行制动力调节使滑移率在制动过程处于最佳范围,保证系统具有良好制动性能。 汽车的制动液压调节器主要包含以下几个部件:调压电磁…...
IOS开发者证书快捷申请
App Uploader 在进行iOS应用开发中,可以借助appuploader辅助工具进行证书制作、上传和安装测试等操作。首先,您需要访问官方网站获取最新版本的appuploader。最新版本已经优化了与Apple账号的登录流程,无需支付688元,并提供了Windows版和Mac版供用户选择。下载完成后,解压…...

python 火焰检测
在日常生活,总是离不开火,有时候我们需要预防火灾发生,但是我们又不可能一直盯着,这时候我们就需要一款程序帮我们盯着,一旦发生火灾从而告知我们,今天就带大家编写这么一款应用。 安装需要的库 pip install opencv-python 代码实现 import cv2 # Library for…...

栈——顺序存储
#include<stdio.h> #define MaxSize 10 //栈的所有操作时间复杂度都是O(1) //定义 typedef struct{int data[MaxSize];int top; //栈顶指针,永远指向栈顶元素 }SqStack;//初始化,使栈顶指针指向-1 void InitStack(SqStack &S){S.top-1; }…...
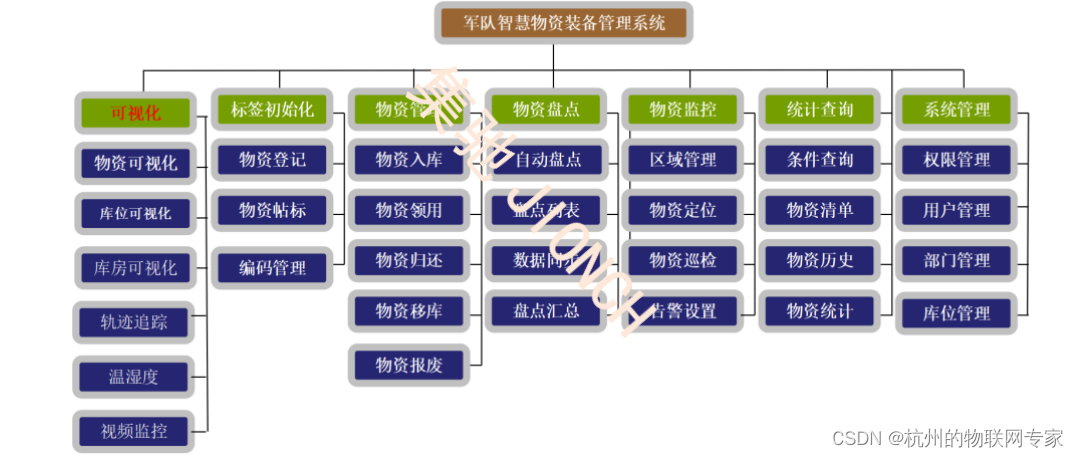
军队仓库管理系统|DW-S301系统特点
部队仓库管理系统DW-S301系统通过数据采集、互联网和物联网技术,实现数字化智能管控,以提高军用物资的仓储准确率和流转率,缩短周转时间,降低库存成本,也有助于消除生产过程中的不确定性。 系统功能:通过部…...

MySQL和MongoDB数据库的区别
MySQL和MongoDB数据库的区别 随着大数据和云计算技术的兴起,数据库的选择成为开发者和架构师必须面对的重要决策。MySQL和MongoDB作为关系型数据库和非关系型数据库的代表,在各自领域都有着广泛的应用。本文将从多方面详细比较MySQL和MongoDB࿰…...

类脑计算和量子计算、人工智能的关系
According to www.iAsk.ai Ask Ai Search Engine: 类脑计算、量子计算和人工智能是三个不同但相关的领域。它们在不同层面上探索和利用了不同的计算模型和技术,但都旨在推动计算能力的发展和创新。 类脑计算是一种受到人脑神经系统启发的计算模型。它试图通过模拟…...
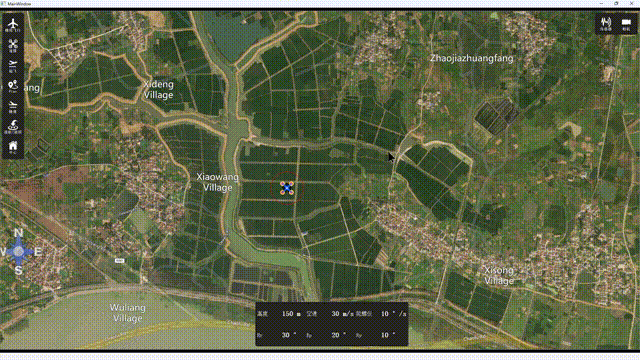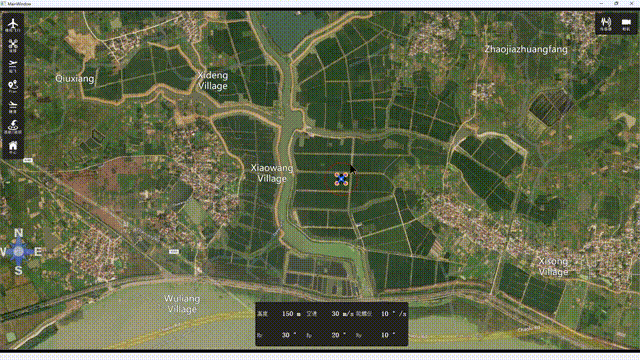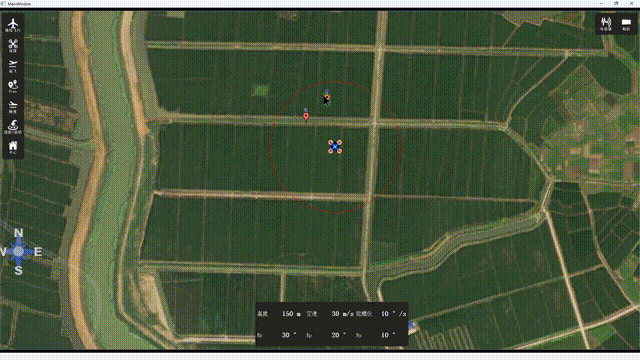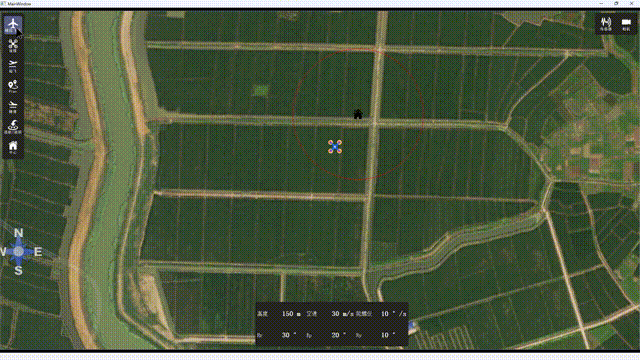
Qt5 互动地图,实现无人机地面站效果
一、概述 本文主要通过Qt5opmapcontrol实现一个简单的无人机地面站效果。opmapcontrol是一个比较古老的QT开源地面站库,可选择谷歌地图,必应地图, 雅虎地图,GIS等。可直接使用源码,也可以编译生成库进行调用。实现效果…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
