【LeetCode】438.找到字符串中所有字母异位词
找到字符串中所有字母异位词
题目描述:
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
思路分析:
依然是滑动窗口法
根据题目要求,我们需要在字符串 s寻找字符串 p 的异位词。因为字符串 p 的异位词的长度一定与字符串 p的长度相同,所以我们可以在字符串 s中构造一个长度为与字符串 p 的长度相同的滑动窗口,并在滑动中维护窗口中每种字母的数量;当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时,则说明当前窗口为字符串 p 的异位词。
优化思路
在上述方法的基础上,我们不再分别统计滑动窗口和字符串中每种字母的数量,而是统计滑动窗口和字符串 p中每种字母数量的差;并引入变量cnt来记录当前窗口与字符串 p中数量不同的字母的个数,并在滑动窗口的过程中维护它。
在判断滑动窗口中每种字母的数量与字符串 p中每种字母的数量是否相同时,只需要判断cnt是否为零即可。
代码实现注解:
class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer>res=new ArrayList<>();//定义一个一维数组记录字母在两个字符串中出现的差值//cnt[x] = 0 表示 s与p中字母x出现次数相同 都出现了n次//cnt[x] = n 表示 在s中字母x出现次数比p多 多出现了n次//cnt[x] = -n 表示 在s中字母x出现次数比p少 少出现了n次int[]cnt=new int[26];//统计字符数量int n=p.length();int m=s.length();//如果目标字符长度大于原始字符长度,返回空数组if(n>m){return res;}//开始遍历数组,创造窗口滑块,p数组出现的字母数值加一,S数组出现的字母数字减一。//所以当cnt数组上的数值为0是代表在滑块中p和s出现该字母的频率一致for(int i=0;i<n-1;i++){cnt[p.charAt(i)-'a']++;cnt[s.charAt(i)-'a']--;}//将P字符串中的最后一个字母读入cnt中cnt[p.charAt(n-1)-'a']++;int l=0;//将S字符串中的n-1位置上的字母作为滑块的右边界//开始滑动窗口for(int r=n-1;r<m;r++){cnt[s.charAt(r)-'a']--;int o=0;//随着右边界的右移,判断新的右边界。如果cnt数组上的数值为0,那么o赋值为1for(int j=0;j<26;j++){o+=cnt[j]==0?1:0;}//说明s和p的同一个字母出现频率相等if(o==26){res.add(l);}//左边界向右移,缩小窗口cnt[s.charAt(l++)-'a']++;}return res;}
}相关文章:

【LeetCode】438.找到字符串中所有字母异位词
找到字符串中所有字母异位词 题目描述: 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。 异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。 示…...

力扣96. 不同的二叉搜索树
Problem: 96. 不同的二叉搜索树 文章目录 题目描述思路复杂度Code 题目描述 思路 一个数字做根节点的话可能的结果为:其左边数字做子树的组合数字乘以其右边数字做子树的个数之积 1.创建备忘录memo; 2.递归分别求取当前数字左边和右边数字做子树的数量&…...

哈希表的用途
...

k8s笔记 | 高度调度
CronJob计划任务 简介:在k8s中周期性运行计划任务,与linux中的crontab相同;注意点 CornJob执行的时间是controller-manager的时间,所以一定要确保controller-manager的时间是准确的,另外cornjob cron表达式 文章参…...

Rom应用开发遇到得一些小bug
记录一些细碎得bug ROM时间类问题 问题描述: 设备拔电重启,ROM时间为默认时间如1970年1月1日,与某些业务场景互斥 问题原因: 后台接口校验https证书校验失败,要求是2年内得请求头校验了时间戳,时间戳过期…...

Python简介
Python简介 1. Python定义 Python 是一种简单易学并且结合了解释性、编译性、互动性和面向对象的脚本语言。Python提供了高级数据结构,它的语法和动态类型以及解释性使它成为广大开发者的首选编程语言。 Python 是解释型语言: 开发过程中没有了编译这个环…...
C++完成特色旅游管理信息系统
背景: 继C完成淄博烧烤节管理系统后,我们来到了特色旅游管理信息系统的代码编写,历史链接点下方。 C完成淄博烧烤节管理系统_淄博烧烤总账管理系统的-CSDN博客 问题描述: 为了更好的管理各个服务小组,开发相应的管…...
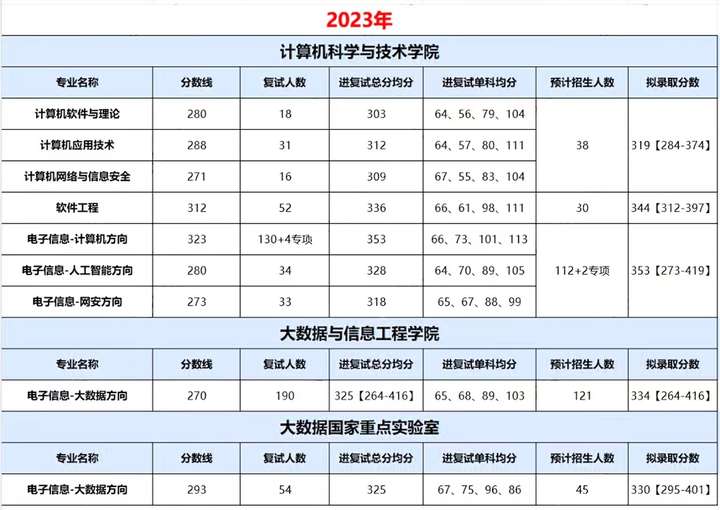
贵州大学24计算机考研数据速览,国家重点实验室22408复试线285分!贵州大学计算机考研考情分析!
贵州大学计算机科学与技术学院坐落在贵州大学北校区(贵阳花溪)。 学院现有教职工139人,其中专职教师126人,教授17人,副教授37人,讲师46人,高级实验师4人,实验师17人。具有博士学位的…...

分区4K对齐那些事,你想知道的都在这里
在对磁盘进行分区时,有一个很重要的注意事项,就是要将分区对齐,不对齐可能会造成磁盘性能的下降。尤其是固态硬盘SSD,基本上都要求4K对齐。磁盘读写速度慢还找不到原因?可能就是4K对齐的锅。那么分区对齐究竟是怎么回事?为什么要对齐?如何才能对齐?如何检测是否对齐呢?…...

达梦数据库学习笔记
架构、特点和基本概念 达梦数据库(DM Database)是中国达梦数据库有限公司自主研发的关系型数据库管理系统。它广泛应用于政府、金融、电信、能源等行业,具备高性能、高可靠性和高安全性的特点。 架构 达梦数据库的架构设计注重高性能和高可…...

安卓绕过限制直接使用Android/data无需授权,支持安卓14(部分)
大家都知道,安卓每次更新都会给权限划分的更细、收的更紧。 早在安卓11的时候还可以直接通过授权Android/data来实现操作其他软件的目录,没有之前安卓11授权的图了,反正都长一个样,就直接贴新图了。 后面到了安卓12~13的…...

【知识蒸馏】多任务模型 logit-based 知识蒸馏实战
一、什么是逻辑(logit)知识蒸馏 Feature-based蒸馏原理是知识蒸馏中的一种重要方法,其关键在于利用教师模型的隐藏层特征来指导学生模型的学习过程。这种蒸馏方式旨在使学生模型能够学习到教师模型在特征提取和表示方面的能力,从…...

C:技术面试总结
1 变量的声明和定义: 定义:为变量分配地址和存储空间 声明:不分配地址。一个变量可以在多个地方声明,但只能在一个地方定义。extern修饰的变量声明,说明此变量将在文件以外或文件后面部分定义。 2 局部变量是否能与全局变量重名: 可以,局部变量会屏蔽全局变量 局部…...

OpenHarmony 实战开发——一文总结ACE代码框架
一、前言 ACE_Engine框架是OpenAtom OpenHarmony(简称“OpenHarmony”)的UI开发框架,为开发者提供在进行应用UI开发时所必需的各种组件,以及定义这些组件的属性、样式、事件及方法,通过这些组件可以方便进行OpenHarmo…...

【数据结构与算法】之堆的应用——堆排序及Top_K问题!
目录 1、堆排序 2、Top_K问题 3、完结散花 个人主页:秋风起,再归来~ 数据结构与算法 个人格言:悟已往之不谏,知来者犹可追 克心守己,律己则安! 1、堆排序 对一个无序的数组…...
啊哈!算法-第2章-栈、队列、链表
啊哈!算法-第2章-栈、队列、链表 第1节 解密qq号——队列第2节 解密回文——栈第3节 纸牌游戏——小猫钓鱼第4节 链表第5节 模拟链表 第1节 解密qq号——队列 新学期开始了,小哈是小哼的新同桌(小哈是个大帅哥哦~),小哼向小哈询问 QQ 号, 小…...

简述 v-if 和 v-show 的区别
v-if 和 v-show 都是 Vue.js 中用于控制元素显示与隐藏的指令,但它们的工作方式有显著的差异。以下是它们之间的主要区别: 渲染方式: v-if:v-if 是“真正”的条件渲染,因为它会确保在切换过程中条件块内的事件监听器和…...

Linux驱动学习之模块化,参数传递,符号导出
1.模块化 1.1.模块化的基本概念: 模块化是指将特定的功能或组件独立出来,以便于开发、测试和维护。在Linux设备驱动中,模块化允许将驱动程序作为内核模块动态加载到系统中,从而提高了系统的灵活性和可扩展性。 1.2.Linux内核模…...

RabbitMQ02-RebbitMQ简介及交换器
一. AMQP协议 什么是AMQP协议 AMQP(Advanced Message Queuing Protocol,高级消息队列协议):它是进程之间传递异步消息的网络协议 AMQP工作过程 发布者通过发布消息,通过交换机,交换机根据路由规则将收到的消息分发交换机绑定的下消息队列,最…...

Matlab自学笔记三十:元胞数组的修改、添加、删除和连接
1.说明 元胞数组的子数组或元素也是元胞型的,其元素内容(值)是本身类型,因此,在添、删、改和连接处理时,必须明确每个元素的值的类型和大小,否则,编程报错是不可避免的了。看本文前…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
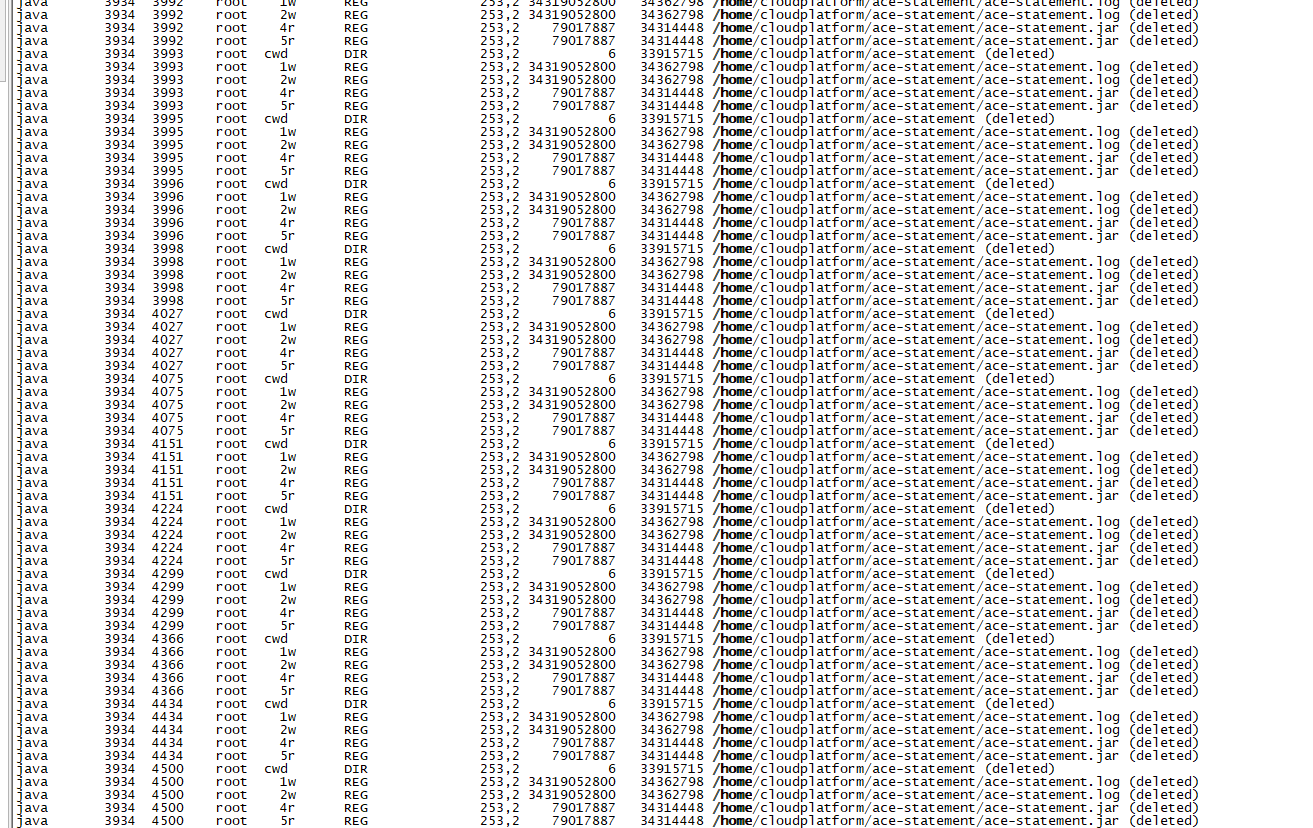
centos挂载目录满但实际未满引发系统宕机
测试服务器应用系统突然挂了,经过排查发现是因为磁盘“满了”导致的,使用df -h查看磁盘使用情况/home目录使用率已经到了100%,但使用du -sh /home查看发现实际磁盘使用还不到1G,推测有进程正在写入或占用已删除的大文件(Linux 系统…...
