【数据结构与算法】之堆的应用——堆排序及Top_K问题!
目录
1、堆排序
2、Top_K问题
3、完结散花
个人主页:秋风起,再归来~
数据结构与算法
个人格言:悟已往之不谏,知来者犹可追
克心守己,律己则安!
1、堆排序
对一个无序的数组,因为数组中的元素是连续的,那我们就可以将数组中的元素进行建堆排序!
假设我们要对一个数组中的元素进行降序,那我们就要先将其进行向下调整建小堆,再将堆顶元素与堆的最后一个元素交换,那么数组中最小的那个元素就到最后面去了,最后一个数有序后,那我们就不再把它看作堆的元素了,最后再在堆顶进行向下调整保证小堆不变。这是一趟,假设数组中有N个元素,那我们进行(N-1)趟就行了。
下面是图解:
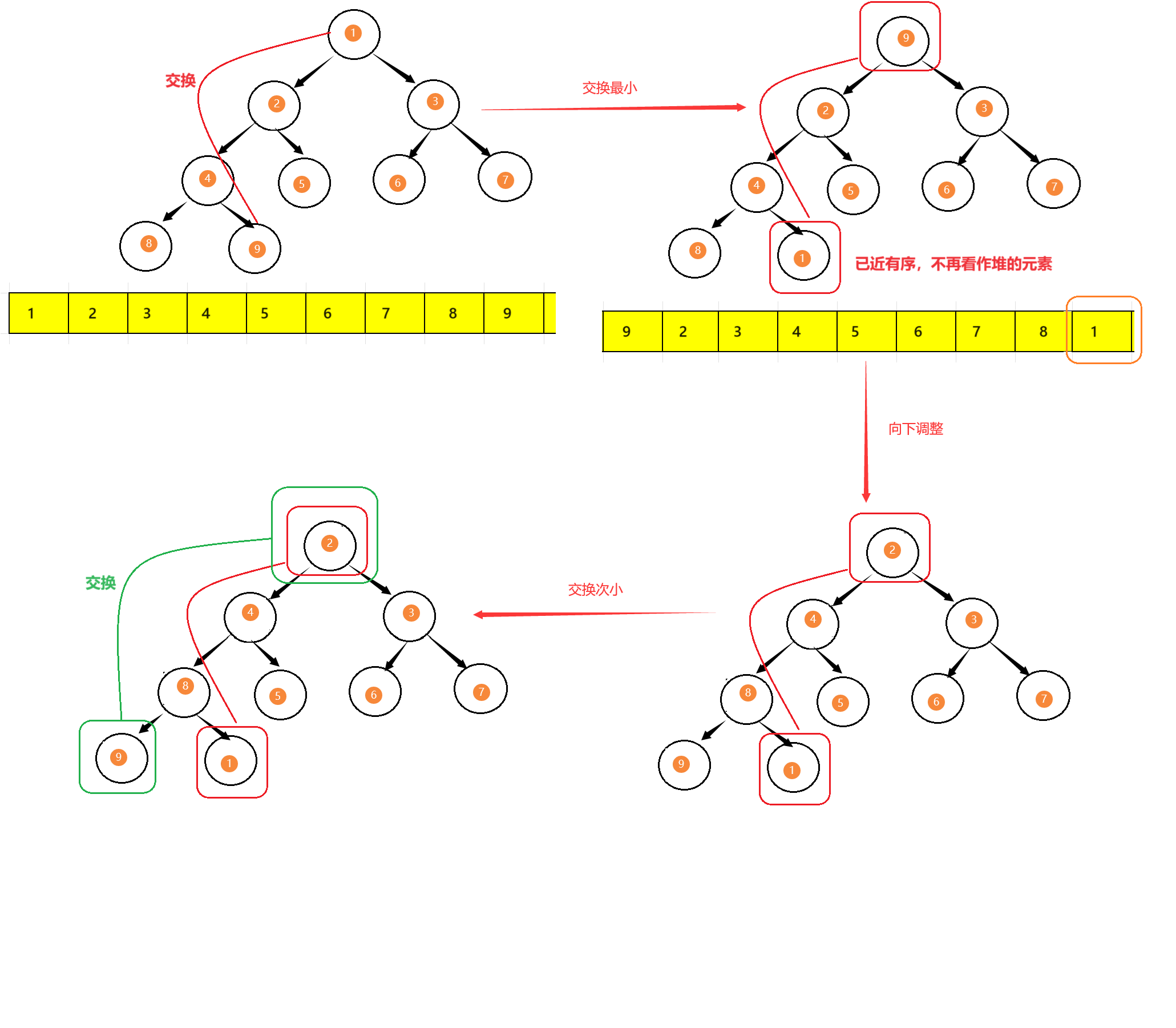
代码:
//交换
void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}//向上调整
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent])//< 建小堆;> 建大堆{swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整
void AdjustDown(int* a, int size, int parent)
{//先假设做孩子小int child = parent * 2 + 1;while (child < size)//当孩子超过最后一个叶子时结束循环{if ((child + 1 < size) && a[child + 1] < a[child])//如果右孩子小于左孩子,右孩子与父亲比较{child++;}if (a[child] < a[parent])//建小堆,即小的当父亲{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆排序
void HeapSort(int* a, int len)
{//建堆算法一(从第一个孩子向上调整)//这种写法的时间复杂度为n*logn//for (int i = 1; i < len; i++)//{// AdjustUp(a, i);//从第一个孩子向上调整建堆//}// //建堆算法二(从倒数第一个根向下调整)//这种写法的时间复杂度为O(N)[更优]for (int i = (len-1-1)/2; i >= 0; i--){AdjustDown(a, len,i);//从倒数第一个根向下调整建堆}int end = len - 1;while (end > 0){swap(&a[0], &a[end]);//交换第一个数与最后一个数end--;AdjustDown(a, end, 0);}
}int main()
{int a[] = { 1,2,4,5,6,8,9,10 };int len = sizeof(a) / sizeof(a[0]);HeapSort(a, len);for (int i = 0; i < len; i++){printf("%d ", a[i]);}return 0;
}
2、Top_K问题
Top_K问题:
Top_K问题就是在大量数据中找出最大或最小的前K个
我们可以很轻松的想到用将这些全部数据进行建堆,在进行K次pop,这样我们就很容易的就可以找到最大或最小的前K个。但这里有一个问题,就是存储这么的数据势必会用到大量的空间,那我们有没有其他方法,在用到极小的的空间内解决问题呢?
当然可以!
假设我们要找出最大的前K个~
1、我们先将全部数据的前K个建成小堆
2、再将后N-K个数据分别和堆顶数据比较,比堆顶数据大就将堆顶数据覆盖
3、然后再从堆顶向下调整保持小堆结构
4、将后N-K个数据比较完后,小堆里面的数据就是最大的前K个
我这里先随机生成10万个随机数并且这些随机数都小于10万,并将这些数据都写进我们的文本文件中!
void CreatRandomNumber()
{FILE* pf = fopen("test.txt", "w");if (pf == NULL){perror("fopen fail!\n");return;}srand((unsigned int)time(NULL));int n = 100000;//随机生成10万个数for (int i = 0; i < n; i++){int x = (rand() + i) % 100000;//这些数的大小都小于10万(方便后面检测)fprintf(pf, "%d\n", x);//将数据写入文件当中}fclose(pf);
}void TestTopK()
{FILE* pf = fopen("test.txt", "r");if (pf == NULL){perror("fopen fail!\n");return;}int k = 0;printf("请输入您要的前K个数:");scanf("%d", & k);int* HeapTopK = (int*)malloc(sizeof(int) * k);//在文件中读取K个数放到数组中for (int i = 0; i < k; i++){fscanf(pf, "%d", &HeapTopK[i]);}//将这K个数建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(HeapTopK, k, i);//向下调整建堆}int x = 0;//在10万个数中找前K个数while (fscanf(pf, "%d", &x)>0){if (x > HeapTopK[0]){HeapTopK[0] = x;AdjustDown(HeapTopK, k, 0); }}HeapSort(HeapTopK, k);//打印前k个数for (int i = 0; i < k; i++){printf("%d ", HeapTopK[i]);}free(HeapTopK);HeapTopK = NULL;fclose(pf);
}
int main()
{//CreatRandomNumber();TestTopK();return 0;
}为了检查结果是否准确,我在文件中随机将10个数的大小手动调整成大于十万!

让我们来看看结果!

3、完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~


相关文章:

【数据结构与算法】之堆的应用——堆排序及Top_K问题!
目录 1、堆排序 2、Top_K问题 3、完结散花 个人主页:秋风起,再归来~ 数据结构与算法 个人格言:悟已往之不谏,知来者犹可追 克心守己,律己则安! 1、堆排序 对一个无序的数组…...
啊哈!算法-第2章-栈、队列、链表
啊哈!算法-第2章-栈、队列、链表 第1节 解密qq号——队列第2节 解密回文——栈第3节 纸牌游戏——小猫钓鱼第4节 链表第5节 模拟链表 第1节 解密qq号——队列 新学期开始了,小哈是小哼的新同桌(小哈是个大帅哥哦~),小哼向小哈询问 QQ 号, 小…...

简述 v-if 和 v-show 的区别
v-if 和 v-show 都是 Vue.js 中用于控制元素显示与隐藏的指令,但它们的工作方式有显著的差异。以下是它们之间的主要区别: 渲染方式: v-if:v-if 是“真正”的条件渲染,因为它会确保在切换过程中条件块内的事件监听器和…...

Linux驱动学习之模块化,参数传递,符号导出
1.模块化 1.1.模块化的基本概念: 模块化是指将特定的功能或组件独立出来,以便于开发、测试和维护。在Linux设备驱动中,模块化允许将驱动程序作为内核模块动态加载到系统中,从而提高了系统的灵活性和可扩展性。 1.2.Linux内核模…...

RabbitMQ02-RebbitMQ简介及交换器
一. AMQP协议 什么是AMQP协议 AMQP(Advanced Message Queuing Protocol,高级消息队列协议):它是进程之间传递异步消息的网络协议 AMQP工作过程 发布者通过发布消息,通过交换机,交换机根据路由规则将收到的消息分发交换机绑定的下消息队列,最…...

Matlab自学笔记三十:元胞数组的修改、添加、删除和连接
1.说明 元胞数组的子数组或元素也是元胞型的,其元素内容(值)是本身类型,因此,在添、删、改和连接处理时,必须明确每个元素的值的类型和大小,否则,编程报错是不可避免的了。看本文前…...

【LeetCode】数组——双指针法
1 双指针法 1.1 介绍 双指针法是一种常用的算法技巧,通常用于处理数组或链表中的问题。它使用两个指针,通常一个从数组的开始位置遍历,另一个从数组的末尾位置开始遍历,根据问题的不同,这两个指针可以同时移动&#…...

react 低代码平台方案汇总
React作为当前最流行的前端框架之一,其生态系统中孕育了多种低代码平台方案,旨在加速应用开发过程。以下是几款基于React的低代码平台或工具,它们通过可视化构建、预制组件、数据绑定等功能,帮助开发者快速构建应用程序࿱…...

oss对象上传文件设置格式
PostMapping("upload")ApiOperation(value "上传文件")public Result<UploadDTO> upload(RequestParam("file") MultipartFile file) throws Exception {if (file.isEmpty()) {return new Result<UploadDTO>().error(ModuleErrorCo…...

【Linux学习】进程
下面是有关进程的相关介绍,希望对你有所帮助! 小海编程心语录-CSDN博客 目录 1. 进程的概念 1.1 进程与程序 1.2 进程号 2. 进程的状态 2.1 fork创建子进程 2.2 父子进程间的文件共享 3. 进程的诞生与终止 3.1 进程的诞生 3.2 进程的终止 1. 进…...

Python数据分析实验四:数据分析综合应用开发
目录 一、实验目的与要求二、主要实验过程1、加载数据集2、数据预处理3、划分数据集4、创建模型估计器5、模型拟合6、模型性能评估 三、主要程序清单和运行结果四、实验体会 一、实验目的与要求 1、目的: 综合运用所学知识,选取有实际背景的应用问题进行…...

基于51单片机的盆栽自动浇花系统
一.硬件方案 工作原理是湿度传感器将采集到的数据直接传送到ADC0832的IN端作为输入的模拟信号。选用湿度传感器和AD转换,电路内部包含有湿度采集、AD转换、单片机译码显示等功能。单片机需要采集数据时,发出指令启动A/D转换器工作,ADC0832根…...
SpirngMVC框架学习笔记(一):SpringMVC基本介绍
1 SpringMVC 特点&概述 SpringMVC 从易用性,效率上 比曾经流行的 Struts2 更好 SpringMVC 是 WEB 层框架,接管了 Web 层组件, 比如控制器, 视图, 视图解析, 返回给用户的数据格式, 同时支持 MVC 的开发模式/开发架构SpringMVC 通过注解,…...

实现信号发生控制
1. 信号发生器的基本原理 信号发生器是一种能够产生特定波形和频率的电子设备,常用于模拟信号的产生和测试。 信号发生器的基本原理 信号发生器的工作原理基于不同的技术,但最常见的类型包括模拟信号发生器和数字信号发生器(DDS࿰…...
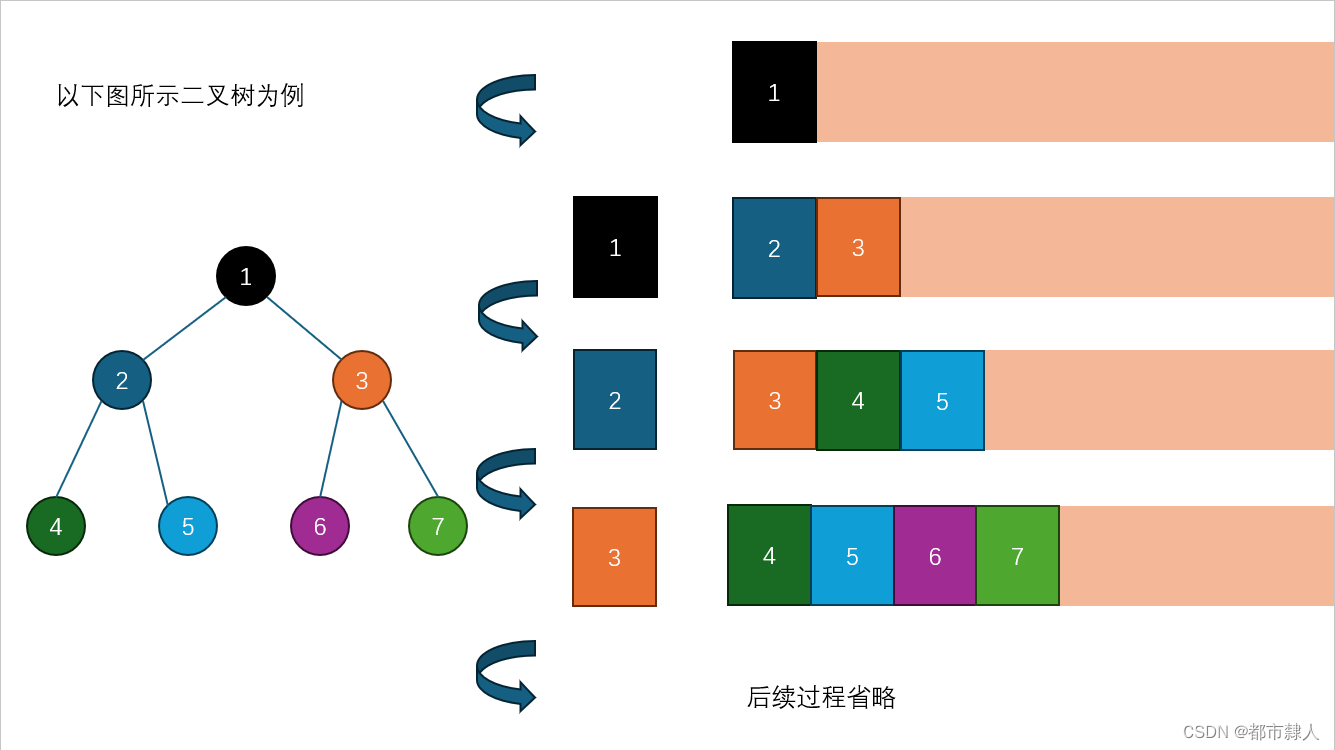
二叉树基于队列实现的操作详解
一、队列知识补充 有关队列的知识请详见博主的另一篇博客:http://t.csdnimg.cn/3PwO4 本文仅仅附上需要的队列操作供读者参考 //结构体定义 typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode {struct QueueNode* next;QDataType val; }QNode;…...

LabVIEW常用开发架构有哪些
LabVIEW常用开发架构有多种,每种架构都有其独特的特点和适用场合。以下是几种常用的开发架构及其特点和适用场合: 1. 单循环架构 特点: 简单易用适用于小型应用将所有代码放在一个循环中 适用场合: 简单的数据采集和处理任务…...
)
告别 Dart 中的 Future.wait([])
作为 Dart 开发人员,我们对异步编程和 Futures 的强大功能并不陌生。过去,当我们需要同时等待多个 future 时,我们依赖 Future.wait([]) 方法,该方法返回一个 List<T>。然而,这种方法有一个显着的缺点࿱…...

Cisco ASA防火墙抓包命令Capture
在日常运维中,遇到故障时经常需要在ASA上抓包进行诊断。 从抓包中可以看到流量是否经过ASA流量是否被ASA放行,或block,匹配的哪一条ACL capture在Firepower平台上同样适用,无论跑的是ASA还是FTD 1 抓包命令 capture 2 配置方…...

Linux网络编程:HTTP协议
前言: 我们知道OSI模型上层分为应用层、会话层和表示层,我们接下来要讲的是主流的应用层协议HTTP,为什么需要这个协议呢,因为在应用层由于操作系统的不同、开发人员使用的语言类型不同,当我们在传输结构化数据时&…...

HTTP 协议中 GET 和 POST 有什么区别?分别适用于什么场景?
HTTP 协议中 GET 和 POST 是两种常用的请求方法,它们的区别如下: 1. 参数传递方式不同 GET 请求参数是在 URL 中以键值对的形式传递的,例如:http://www.example.com/?key1value1&k ey2value2。 而 POST 请求参数是在请求体中以键值对的…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

