二叉树基于队列实现的操作详解
一、队列知识补充
有关队列的知识请详见博主的另一篇博客:http://t.csdnimg.cn/3PwO4
本文仅仅附上需要的队列操作供读者参考
//结构体定义
typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;//入队
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = InitNewnode(x);if (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}
//出队
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size != 0);if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QNode* temp = pq->phead->next;free(pq->phead);pq->phead = temp;}pq->size--;
}
//取出队头元素
QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->phead);return pq->phead->val;
}
//销毁队列
void QueueDestroy(Queue* pq)
{assert(pq);QNode* pcur = pq->phead;while (pcur){QNode* temp = pcur->next;free(pcur);pcur = temp;}pq->phead = pq->ptail = NULL;pq->size = 0;
}二、层序遍历
2.1 递归思路
采用队列先进先出的特点,按照层序入队即可按照层序出队,从而达到层序遍历的目的。
考虑一般情况:
将根节点入队,下一次根节点出队的同时将孩子结点入队。
考虑特殊情况:
孩子结点可看作子树的根节点,重复递归即可。
只要队列不为空就一直递归
2.2 图解
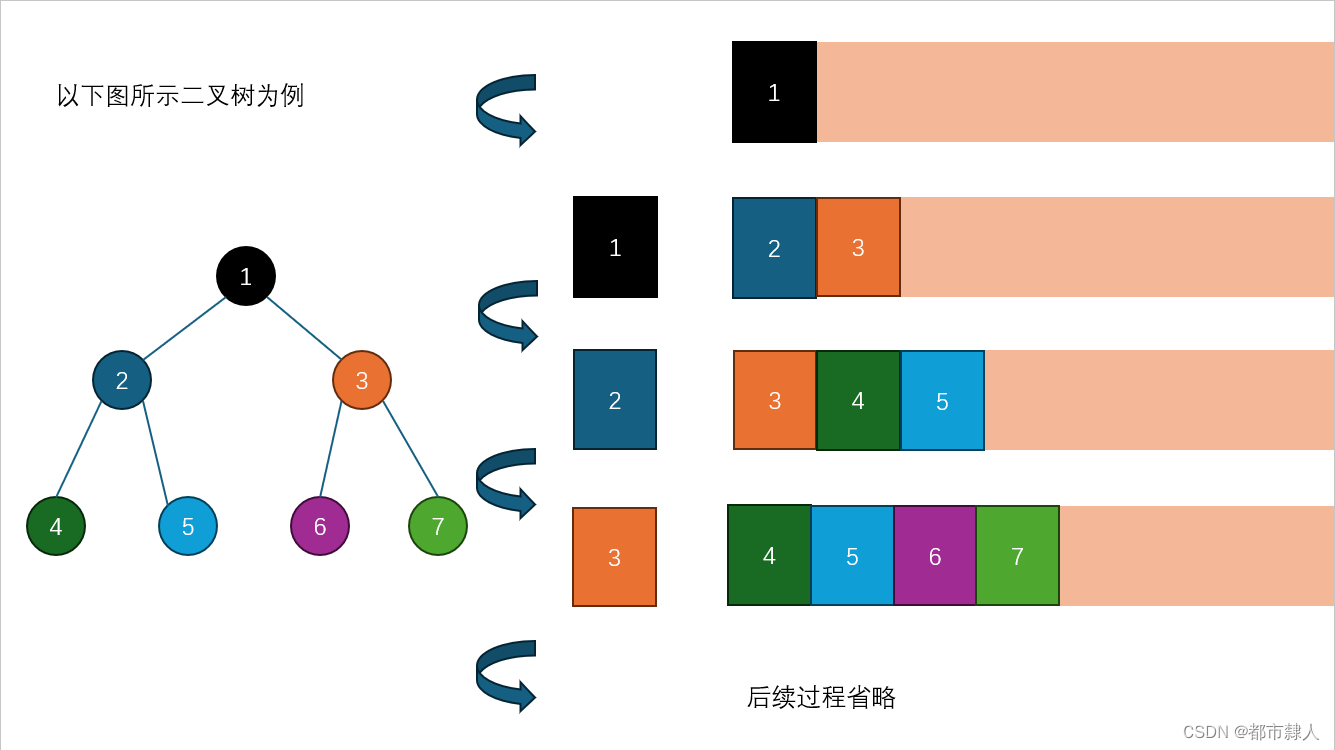
2.3 C语言实现
注意:出队入队要额外新建变量来复制结点,避免销毁队列引发的原二叉树丢失的问题。
void TreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (QueueEmpty(&q)==false){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}QueueDestroy(&q);
}三、判断一棵树是不是完全二叉树
3.0 回顾
什么是完全二叉树?完全二叉树是一种特殊的二叉树,其中除了最后一层外,每一层的节点都被填满,而且最后一层的节点都尽可能地靠左排列。换句话说,如果一个层次深度为k的树,除了第 k 层外,其他各层都是满的,并且第 k 层的节点都依次靠左排列,则这棵树就是完全二叉树。
所以仅仅通过判断结点的范围处于k-1层满二叉树和k层满二叉树之间的解法是错误的!!
3.1 思路
通过层序遍历,将第一次出现空结点的地方找到,只需判断后续遍历的过程中是否存在非空结点即可,若存在就不是完全二叉树,反之则是。
分两个循环解决该问题。
- 第一层循环本质即为层序遍历,找到第一个空节点就退出。
- 第二层循环依然为层序遍历,看是否可以找到非空结点。当队列里面没有元素即层序遍历结束时判断完成。
3.2 C语言实现
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL){QueuePush(&q, root);}//入队遇到空停止入队while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//判断后面是否还有非空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){return false;}}QueueDestroy(&q);return true;
}相关文章:

二叉树基于队列实现的操作详解
一、队列知识补充 有关队列的知识请详见博主的另一篇博客:http://t.csdnimg.cn/3PwO4 本文仅仅附上需要的队列操作供读者参考 //结构体定义 typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode {struct QueueNode* next;QDataType val; }QNode;…...

LabVIEW常用开发架构有哪些
LabVIEW常用开发架构有多种,每种架构都有其独特的特点和适用场合。以下是几种常用的开发架构及其特点和适用场合: 1. 单循环架构 特点: 简单易用适用于小型应用将所有代码放在一个循环中 适用场合: 简单的数据采集和处理任务…...
)
告别 Dart 中的 Future.wait([])
作为 Dart 开发人员,我们对异步编程和 Futures 的强大功能并不陌生。过去,当我们需要同时等待多个 future 时,我们依赖 Future.wait([]) 方法,该方法返回一个 List<T>。然而,这种方法有一个显着的缺点࿱…...

Cisco ASA防火墙抓包命令Capture
在日常运维中,遇到故障时经常需要在ASA上抓包进行诊断。 从抓包中可以看到流量是否经过ASA流量是否被ASA放行,或block,匹配的哪一条ACL capture在Firepower平台上同样适用,无论跑的是ASA还是FTD 1 抓包命令 capture 2 配置方…...

Linux网络编程:HTTP协议
前言: 我们知道OSI模型上层分为应用层、会话层和表示层,我们接下来要讲的是主流的应用层协议HTTP,为什么需要这个协议呢,因为在应用层由于操作系统的不同、开发人员使用的语言类型不同,当我们在传输结构化数据时&…...

HTTP 协议中 GET 和 POST 有什么区别?分别适用于什么场景?
HTTP 协议中 GET 和 POST 是两种常用的请求方法,它们的区别如下: 1. 参数传递方式不同 GET 请求参数是在 URL 中以键值对的形式传递的,例如:http://www.example.com/?key1value1&k ey2value2。 而 POST 请求参数是在请求体中以键值对的…...
talib 安装
这里写自定义目录标题 talib 安装出错 talib 安装出错 https://github.com/cgohlke/talib-build/releases 这里找到轮子 直接装。...
echarts-树图、关系图、桑基图、日历图
树图 树图主要用来表达关系结构。 树图的端点也收symbol的调节 树图的特有属性: 树图的方向: layout、orient子节点收起展开:initialTreeDepth、expandAndCollapse叶子节点设置: leaves操作设置:roam线条:…...
04Django项目基本运行逻辑及模板资源套用
对应视频链接点击直达 Django项目用户管理及模板资源 对应视频链接点击直达1.基本运行逻辑Django的基本运行路线:视图views.py中的 纯操作、数据返回、页面渲染 2.模版套用1.寻找一个好的模版2.模板部署--修改适配联动 OVER,不会有人不会吧不会的加Q1394…...

安徽大学数学科学学院教授陈昌昊
男,本(2005-2009)、硕(2009-2012)学位都在湖北大学获得,博士学位在芬兰获得(2012-2016),博士后分别在澳大利亚(2016-2019)、香港(2020…...

com.alibaba.fastjson.JSONObject循环给同一对象赋值会出现“$ref“:“$[0]“现象问题
1、问题描述 有些场景下,我们会选择用JSONObject代替Map来处理业务逻辑,但是使用JSONObject时有一个需要注意的地方:在处理JSONObject对象时,引用的com.alibaba.fastjson.JSONObject,在一个集合中,循环给这…...

【C++】详解AVL树——平衡二叉搜索树
个人主页:东洛的克莱斯韦克-CSDN博客 祝福语:愿你拥抱自由的风 目录 二叉搜索树 AVL树概述 平衡因子 旋转情况分类 左单旋 右单旋 左右双旋 右左双旋 AVL树节点设计 AVL树设计 详解单旋 左单旋 右单旋 详解双旋 左右双旋 平衡因子情况如…...
《计算机网络微课堂》2-2 物理层下面的传输媒体
请大家注意,传输媒体不属于计算机网络体系结构的任何一层,如果非要将它添加到体系结构中,那只能将其放在物理层之下。 传输媒体可分为两类:一类是导引型传输媒体,另一类是非导引型传输媒体。 在导引型传输媒体…...
【算法设计与分析】基于Go语言实现动态规划法解决TSP问题
本文针对于最近正在学习的Go语言,以及算法课实验所需内容进行Coding,一举两得! 一、前言 由于这个实验不要求向之前的实验一样做到那种连线的可视化,故可以用图形界面不那么好实现的语言进行编写,考虑到Go语言的…...
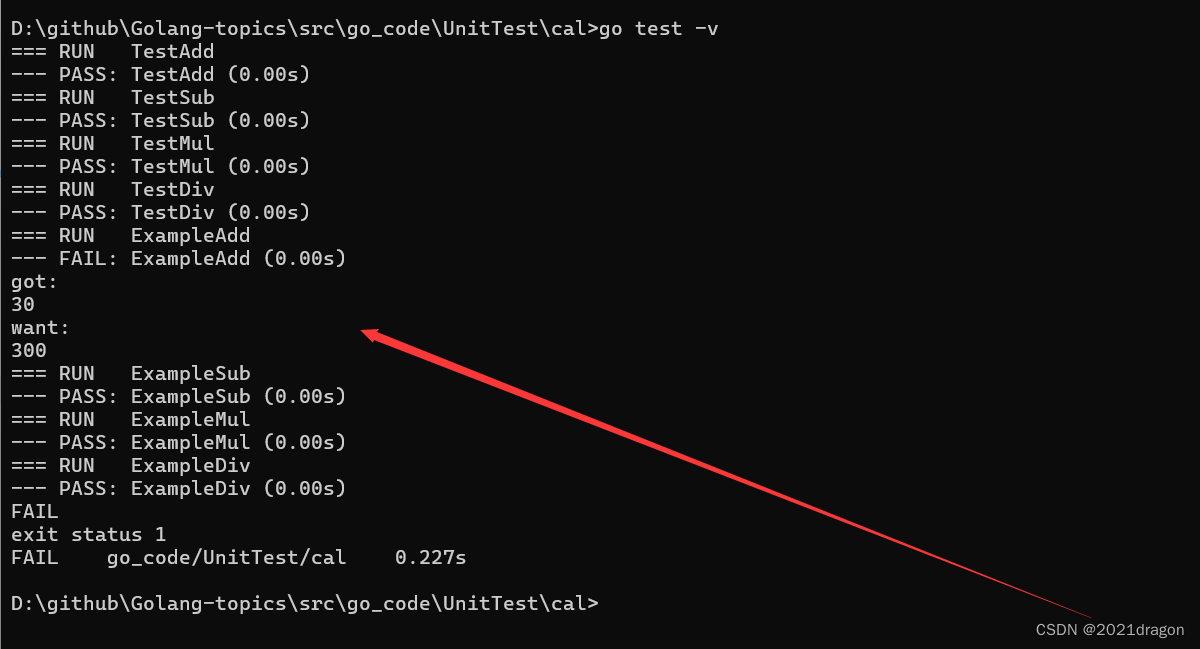
Golang单元测试
文章目录 传统测试方法基本介绍主要缺点 单元测试基本介绍测试函数基准测试示例函数 传统测试方法 基本介绍 基本介绍 代码测试是软件开发中的一项重要实践,用于验证代码的正确性、可靠性和预期行为。通过代码测试,开发者可以发现和修复潜在的错误、确保…...
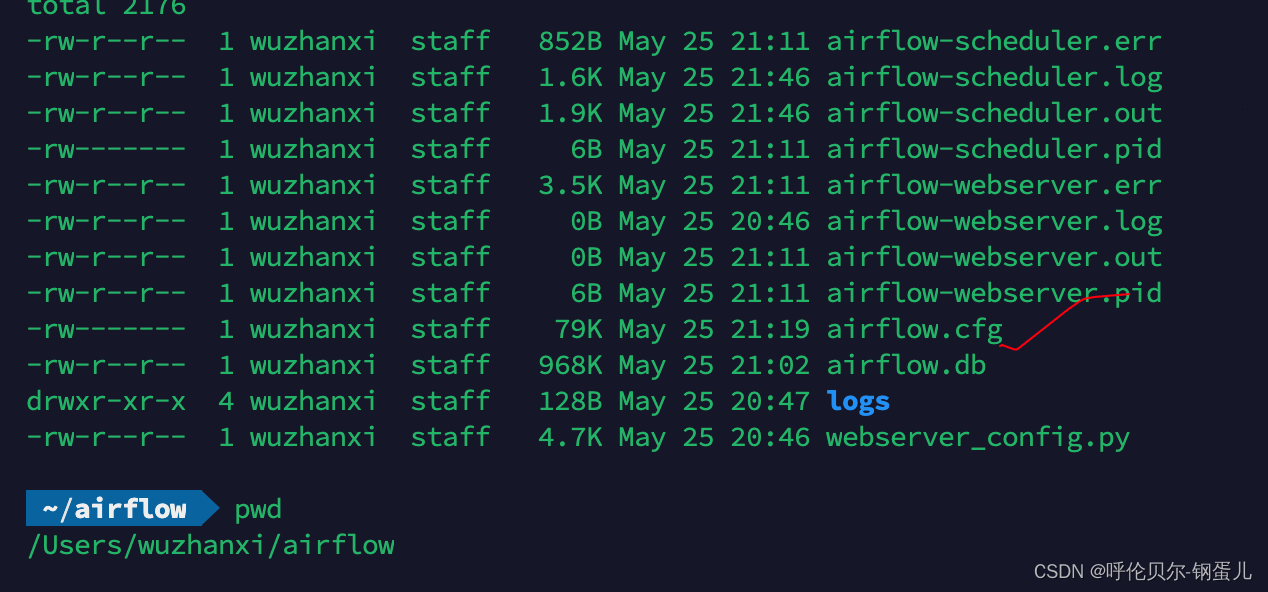
mac下安装airflow
背景:因为用的是Mac的M芯片的电脑,安装很多东西都经常报错,最近在研究怎么把大数据集群上的crontab下的任务都配置到一个可视化工具中,发现airflow好像是个不错的选择,然后就研究怎么先安装使用起来,后面再…...

二进制中1的个数c++
题目描述 计算鸭给定一个十进制非负整数 NN,求其对应 22 进制数中 11 的个数。 输入 输入包含一行,包含一个非负整数 NN。(N < 10^9) 输出 输出一行,包含一个整数,表示 NN 的 22 进制表示中 11 的个数。 样例输入 100 …...

【面试干货】数据库乐观锁,悲观锁的区别,怎么实现
【面试干货】数据库乐观锁,悲观锁的区别,怎么实现 1、乐观锁,悲观锁的区别2、总结 💖The Begin💖点点关注,收藏不迷路💖 1、乐观锁,悲观锁的区别 悲观锁(Pessimistic Lo…...
移动端仪表盘,支持更多组件
05/22 主要更新模块概览 定位函数 快捷筛选 轨迹图表 时间组件 01 表单管理 1.1 【表单组件】- 表单关联新增支持自定义按钮样式 说明: 表单关联-关联数据按钮,原仅支持默认按钮样式,现增加关联数据按钮自定义功能,满…...

科技产业园3D探秘:未来科技之城的奇幻之旅
在数字时代的浪潮中,科技产业园区成为了推动城市经济发展、科技创新的重要引擎。 当我们打开科技产业园的3D可视化模型,仿佛穿越时空,来到了一个充满奇幻色彩的科技世界。在这里,高楼大厦鳞次栉比,绿色植被点缀其间&am…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

【向量库】Weaviate 搜索与索引技术:从基础概念到性能优化
文章目录 零、概述一、搜索技术分类1. 向量搜索:捕捉语义的智能检索2. 关键字搜索:精确匹配的传统方案3. 混合搜索:语义与精确的双重保障 二、向量检索技术分类1. HNSW索引:大规模数据的高效引擎2. Flat索引:小规模数据…...
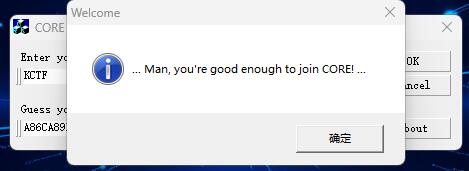
[KCTF]CORE CrackMe v2.0
这个Reverse比较古老,已经有20多年了,但难度确实不小。 先查壳 upx压缩壳,0.72,废弃版本,工具无法解压。 反正不用IDA进行调试,直接x32dbg中,dump内存,保存后拖入IDA。 这里说一下…...

民锋视角下的资金流效率与账户行为建模
民锋视角下的资金流效率与账户行为建模 在当前复杂多变的金融环境中,资金流效率已成为衡量一家金融服务机构专业能力的重要指标。民锋在账户管理与资金调配的实战经验中,逐步建立起一套以资金流路径为核心的行为建模方法,用以评估客户行为、交…...
