【LeetCode】数组——双指针法
1 双指针法
1.1 介绍
双指针法是一种常用的算法技巧,通常用于处理数组或链表中的问题。它使用两个指针,通常一个从数组的开始位置遍历,另一个从数组的末尾位置开始遍历,根据问题的不同,这两个指针可以同时移动,也可以根据条件移动。
1.2 使用场景
双指针法可以用于多种场景,如:
-
1.数组合并:将两个有序数组合并为一个有序数组。
-
2.链表操作:如判断链表是否有环、寻找链表的中点等。
-
3.数组操作:如寻找数组中的两数之和等于特定值的两个数。
-
4.滑动窗口:用于解决数组或字符串的子串问题。
2 LeetCode相关题解
2.1 27. 移除元素
27.移除元素链接
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
思路:一个指针(fast)用来寻找不等于val的元素,另一个指针(slow)将这个元素添加到数组中。
int removeElement(int* nums, int numsSize, int val) {int slow = 0;int fast = 0;for(; fast < numsSize; fast++){if(nums[fast] != val){nums[slow] = nums[fast];slow++;}else continue;}return slow;
}
2.2 26.删除有序数组中的重复项
26.删除有序数组中的重复项链接
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 非严格递增 排列
思路:一个指针(fast)用来寻找新数组(不包含相同元素的数组)中的元素,另一个指针(slow)用来将该元素添加到新数组中。
int removeDuplicates(int* nums, int numsSize) {int slow = 0;int fast = 0;for(;fast < numsSize; fast++){if(nums[slow] != nums[fast]){slow++;nums[slow] = nums[fast];}}return slow+1;
}
2.3 283.移动零
283.移动零链接
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
思路:先使用双指针法将非零元素前移,再将后面的元素赋值为零。
void moveZeroes(int* nums, int numsSize) {int slow = 0;int fast = 0;for(; fast < numsSize; fast++){if(nums[fast] != 0)nums[slow++] = nums[fast];}for(; slow < numsSize; slow++){nums[slow] = 0;}
}
2.4 844.比较含退格的字符串
844.比较含退格的字符串链接
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
注意:如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:s = “ab#c”, t = “ad#c”
输出:true
解释:s 和 t 都会变成 “ac”。
示例 2:
输入:s = “ab##”, t = “c#d#”
输出:true
解释:s 和 t 都会变成 “”。
示例 3:
输入:s = “a#c”, t = “b”
输出:false
解释:s 会变成 “c”,但 t 仍然是 “b”。
提示:
1 <= s.length, t.length <= 200
s 和 t 只含有小写字母以及字符 ‘#’
思路:分别计算出两个字符串最终输出的字符串,再进行对比。
#include <string.h>
char* build(char* s, int len){int j = 0;char* arr = (char*)malloc((len+1) * sizeof(char));if(arr == NULL) {printf("内存分配失败\n");exit(1);}for(int i=0;i < len; i++){if(s[i] == '#'){if (j > 0) {j--;}}else {arr[j++] = s[i];}}arr[j] = '\0';return arr;
}bool backspaceCompare(char * s, char * t){char* c1 = build(s,strlen(s));char* c2 = build(t,strlen(t));if (strcmp(c1, c2) == 0) {return true;}return false;
}
2.5 977.有序数组的平方
977.有序数组的平方链接
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
思路:数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。利用双指针法,从两边开始向中间遍历,比较两边元素平方的大小,大的放到新数组中。
int* sortedSquares(int* nums, int numsSize, int* returnSize) {*returnSize = numsSize;int* ret = (int*)malloc(sizeof(int) *numsSize);int fast = numsSize - 1;int slow = 0;int i = numsSize - 1;while(slow <= fast){if(nums[slow]*nums[slow] > nums[fast]*nums[fast]){ret[i] = nums[slow]*nums[slow];slow++;i--;}else {ret[i] = nums[fast]*nums[fast];fast--;i--;}}return ret;
}
如果在 while(slow <= fast) 改为 while(slow < fast),会漏了 slow == fast 的这个元素。
2.6 209.长度最小的子数组
209.长度最小的子数组链接
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续
子数组
[numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
思路:一个指针用来寻找目标数组的右边界,当目标数组的元素和大于等于目标值时开始移动左边界减小目标数组。(目标数组:元素和大于等于目标值的数组)
int minSubArrayLen(int target, int* nums, int numsSize) {int left = 0;int right = 0;int sum = 0;int lenth = 0;int retlenth = numsSize + 1;for(; right < numsSize; right++){sum += nums[right];while(sum >= target){lenth = right - left + 1;retlenth = retlenth < lenth?retlenth : lenth;sum -= nums[left++];}}if(retlenth == numsSize + 1) return 0;return retlenth;
}
-
关于 retlenth = numsSize + 1 的设定:
-
排除了将数组全加起来仍然小于target的情况;如[1,1,1,1,1] 15。
-
同时也能返回将数组全加起来恰好等于target的情况;如[1,2,3,4,5] 15。
-
-
关于 while(sum >= target) 使用 while 循环而不是 if :
- 如果使用的是if,那么后面的代码只执行一次,但你并不能判断将起始位置(left)后移过的 sum 一定比 target 小
相关文章:

【LeetCode】数组——双指针法
1 双指针法 1.1 介绍 双指针法是一种常用的算法技巧,通常用于处理数组或链表中的问题。它使用两个指针,通常一个从数组的开始位置遍历,另一个从数组的末尾位置开始遍历,根据问题的不同,这两个指针可以同时移动&#…...

react 低代码平台方案汇总
React作为当前最流行的前端框架之一,其生态系统中孕育了多种低代码平台方案,旨在加速应用开发过程。以下是几款基于React的低代码平台或工具,它们通过可视化构建、预制组件、数据绑定等功能,帮助开发者快速构建应用程序࿱…...

oss对象上传文件设置格式
PostMapping("upload")ApiOperation(value "上传文件")public Result<UploadDTO> upload(RequestParam("file") MultipartFile file) throws Exception {if (file.isEmpty()) {return new Result<UploadDTO>().error(ModuleErrorCo…...

【Linux学习】进程
下面是有关进程的相关介绍,希望对你有所帮助! 小海编程心语录-CSDN博客 目录 1. 进程的概念 1.1 进程与程序 1.2 进程号 2. 进程的状态 2.1 fork创建子进程 2.2 父子进程间的文件共享 3. 进程的诞生与终止 3.1 进程的诞生 3.2 进程的终止 1. 进…...

Python数据分析实验四:数据分析综合应用开发
目录 一、实验目的与要求二、主要实验过程1、加载数据集2、数据预处理3、划分数据集4、创建模型估计器5、模型拟合6、模型性能评估 三、主要程序清单和运行结果四、实验体会 一、实验目的与要求 1、目的: 综合运用所学知识,选取有实际背景的应用问题进行…...

基于51单片机的盆栽自动浇花系统
一.硬件方案 工作原理是湿度传感器将采集到的数据直接传送到ADC0832的IN端作为输入的模拟信号。选用湿度传感器和AD转换,电路内部包含有湿度采集、AD转换、单片机译码显示等功能。单片机需要采集数据时,发出指令启动A/D转换器工作,ADC0832根…...
SpirngMVC框架学习笔记(一):SpringMVC基本介绍
1 SpringMVC 特点&概述 SpringMVC 从易用性,效率上 比曾经流行的 Struts2 更好 SpringMVC 是 WEB 层框架,接管了 Web 层组件, 比如控制器, 视图, 视图解析, 返回给用户的数据格式, 同时支持 MVC 的开发模式/开发架构SpringMVC 通过注解,…...

实现信号发生控制
1. 信号发生器的基本原理 信号发生器是一种能够产生特定波形和频率的电子设备,常用于模拟信号的产生和测试。 信号发生器的基本原理 信号发生器的工作原理基于不同的技术,但最常见的类型包括模拟信号发生器和数字信号发生器(DDS࿰…...
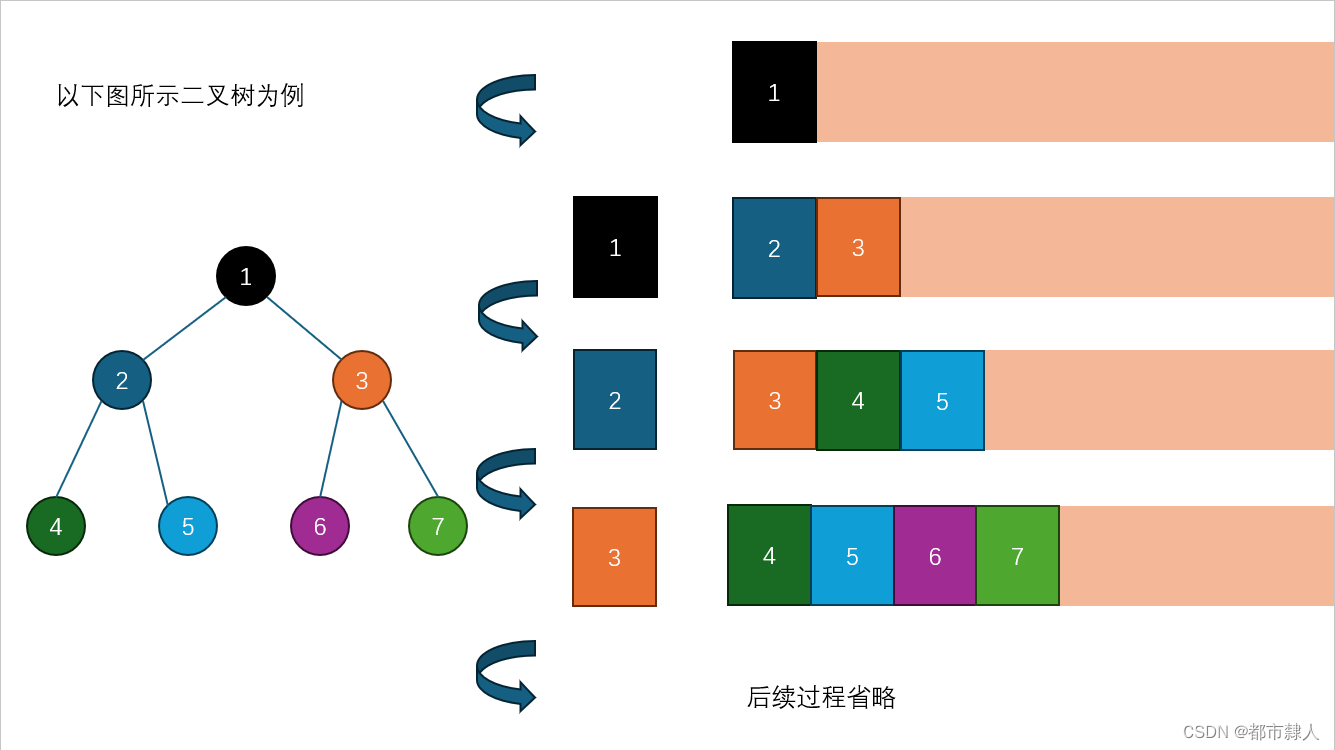
二叉树基于队列实现的操作详解
一、队列知识补充 有关队列的知识请详见博主的另一篇博客:http://t.csdnimg.cn/3PwO4 本文仅仅附上需要的队列操作供读者参考 //结构体定义 typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode {struct QueueNode* next;QDataType val; }QNode;…...

LabVIEW常用开发架构有哪些
LabVIEW常用开发架构有多种,每种架构都有其独特的特点和适用场合。以下是几种常用的开发架构及其特点和适用场合: 1. 单循环架构 特点: 简单易用适用于小型应用将所有代码放在一个循环中 适用场合: 简单的数据采集和处理任务…...
)
告别 Dart 中的 Future.wait([])
作为 Dart 开发人员,我们对异步编程和 Futures 的强大功能并不陌生。过去,当我们需要同时等待多个 future 时,我们依赖 Future.wait([]) 方法,该方法返回一个 List<T>。然而,这种方法有一个显着的缺点࿱…...

Cisco ASA防火墙抓包命令Capture
在日常运维中,遇到故障时经常需要在ASA上抓包进行诊断。 从抓包中可以看到流量是否经过ASA流量是否被ASA放行,或block,匹配的哪一条ACL capture在Firepower平台上同样适用,无论跑的是ASA还是FTD 1 抓包命令 capture 2 配置方…...

Linux网络编程:HTTP协议
前言: 我们知道OSI模型上层分为应用层、会话层和表示层,我们接下来要讲的是主流的应用层协议HTTP,为什么需要这个协议呢,因为在应用层由于操作系统的不同、开发人员使用的语言类型不同,当我们在传输结构化数据时&…...

HTTP 协议中 GET 和 POST 有什么区别?分别适用于什么场景?
HTTP 协议中 GET 和 POST 是两种常用的请求方法,它们的区别如下: 1. 参数传递方式不同 GET 请求参数是在 URL 中以键值对的形式传递的,例如:http://www.example.com/?key1value1&k ey2value2。 而 POST 请求参数是在请求体中以键值对的…...
talib 安装
这里写自定义目录标题 talib 安装出错 talib 安装出错 https://github.com/cgohlke/talib-build/releases 这里找到轮子 直接装。...
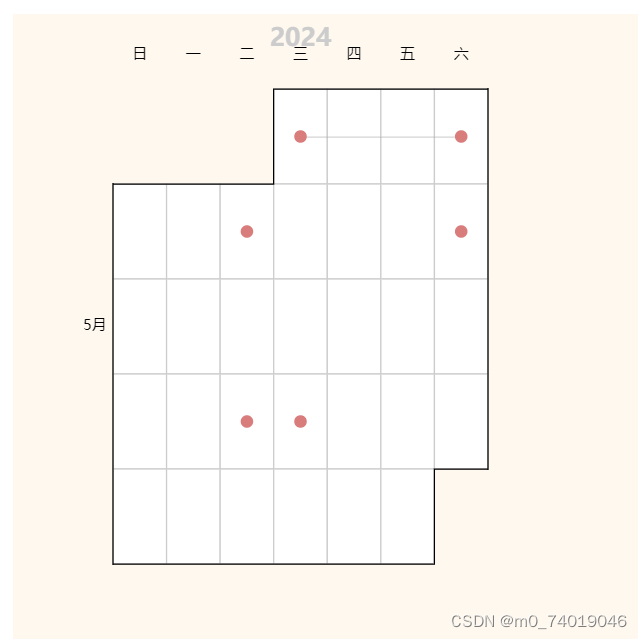
echarts-树图、关系图、桑基图、日历图
树图 树图主要用来表达关系结构。 树图的端点也收symbol的调节 树图的特有属性: 树图的方向: layout、orient子节点收起展开:initialTreeDepth、expandAndCollapse叶子节点设置: leaves操作设置:roam线条:…...
04Django项目基本运行逻辑及模板资源套用
对应视频链接点击直达 Django项目用户管理及模板资源 对应视频链接点击直达1.基本运行逻辑Django的基本运行路线:视图views.py中的 纯操作、数据返回、页面渲染 2.模版套用1.寻找一个好的模版2.模板部署--修改适配联动 OVER,不会有人不会吧不会的加Q1394…...

安徽大学数学科学学院教授陈昌昊
男,本(2005-2009)、硕(2009-2012)学位都在湖北大学获得,博士学位在芬兰获得(2012-2016),博士后分别在澳大利亚(2016-2019)、香港(2020…...

com.alibaba.fastjson.JSONObject循环给同一对象赋值会出现“$ref“:“$[0]“现象问题
1、问题描述 有些场景下,我们会选择用JSONObject代替Map来处理业务逻辑,但是使用JSONObject时有一个需要注意的地方:在处理JSONObject对象时,引用的com.alibaba.fastjson.JSONObject,在一个集合中,循环给这…...

【C++】详解AVL树——平衡二叉搜索树
个人主页:东洛的克莱斯韦克-CSDN博客 祝福语:愿你拥抱自由的风 目录 二叉搜索树 AVL树概述 平衡因子 旋转情况分类 左单旋 右单旋 左右双旋 右左双旋 AVL树节点设计 AVL树设计 详解单旋 左单旋 右单旋 详解双旋 左右双旋 平衡因子情况如…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
