Day21:Leetcode513.找树左下角的值 +112. 路径总和 113.路径总和ii + 106.从中序与后序遍历序列构造二叉树
LeetCode:513.找树左下角的值
解决方案:
1.思路
- 在遍历一个节点时,需要先把它的非空右子节点放入队列,
- 然后再把它的非空左子节点放入队列,这样才能保证从右到左遍历每一层的节点。
- 广度优先搜索所遍历的最后一个节点的值就是最底层最左边节点的值。
class Solution {public int findBottomLeftValue(TreeNode root) {int ret = 0;//基于数组的双端队列Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {TreeNode p = queue.poll();if (p.right != null) {queue.offer(p.right);}if (p.left != null) {queue.offer(p.left);}//如果当前队列不为空。当前根节点既没有左节点,也没有右节点,那么就把此该节点赋值给retret = p.val;}return ret;}
}
3.复杂度分析
LeetCode:112. 路径总和
解决方案:
1.思路:
递归三部曲:
- 函数返回类型和参数;
- 终止条件;
- 递归逻辑
递归逻辑
2.代码实现
public class Solution {private boolean traversal(TreeNode cur, int count) {if (cur.left == null && cur.right == null && count == 0) return true; // 遇到叶子节点,并且计数为0if (cur.left == null && cur.right == null) return false; // 遇到叶子节点直接返回if (cur.left != null) { // 左count -= cur.left.val; // 递归,处理节点;if (traversal(cur.left, count)) return true;count += cur.left.val; // 回溯,撤销处理结果}if (cur.right != null) { // 右count -= cur.right.val; // 递归,处理节点;if (traversal(cur.right, count)) return true;count += cur.right.val; // 回溯,撤销处理结果}return false;}public boolean hasPathSum(TreeNode root, int sum) {if (root == null) return false;return traversal(root, sum - root.val);}
}
3.复杂度分析

LeetCode:113.路径总和ii
解决方案:
1.思路:
- 思路同112
- 但是注意递归函数不再有返回值,而是用一个 path数组接住;然后再用一个result数组接住所有path;
2.代码实现
public class Solution {private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();// 递归函数不需要返回值,因为我们要遍历整个树private void traversal(TreeNode cur, int count) {if (cur.left == null && cur.right == null && count == 0) { // 遇到了叶子节点且找到了和为sum的路径result.add(new ArrayList<>(path));return;}if (cur.left == null && cur.right == null) return; // 遇到叶子节点而没有找到合适的边,直接返回if (cur.left != null) { // 左 (空节点不遍历)path.add(cur.left.val);count -= cur.left.val;traversal(cur.left, count); // 递归count += cur.left.val; // 回溯path.remove(path.size() - 1); // 回溯}if (cur.right != null) { // 右 (空节点不遍历)path.add(cur.right.val);count -= cur.right.val;traversal(cur.right, count); // 递归count += cur.right.val; // 回溯path.remove(path.size() - 1); // 回溯}}public List<List<Integer>> pathSum(TreeNode root, int sum) {result.clear();path.clear();if (root == null) return result;path.add(root.val); // 把根节点放进路径traversal(root, sum - root.val);return result;}
}
3.复杂度分析
- 时间复杂度:O(N),其中N是树中节点的数量。这是因为每个节点在递归过程中会被访问一次。尽管存在递归调用,但每个节点只被访问并处理一次,因此总体时间复杂度线性依赖于树的大小,而不是递归深度。
- 空间复杂度:最坏情况下,当树完全不平衡,且每一条从根到叶子的路径都满足题目条件时,递归的深度达到最大,此时的空间复杂度由递归栈的深度决定,为O(N)。最好情况下(即树完全平衡),递归的最大深度为log(N),因此在这种情况下,空间复杂度为O(log(N))。但由于我们还需要存储路径(path),在最坏情况下(每条边都构成解),这也会占用O(N)的空间。因此,综合考虑,整体的空间复杂度也是O(N)。
LeetCode:106.从中序与后序遍历序列构造二叉树
解决方案:
1.思路:
- 利用遍历特性:中序遍历(左根右)确定节点在序列中的相对位置,后序遍历(左右根)的最后一个元素总是当前子树的根节点
- 递归思想:通过递归不断地将问题分解为更小的子问题,直到达到基础情况(空列表),然后逐层返回,逐步构建整棵树。
- 动态调整遍历列表:每次递归调用前,根据当前子树的信息调整中序和后序遍历列表,确保传入的列表仅对应当前子树的信息。
2.代码实现
import java.util.ArrayList;
import java.util.List;public class Solution {private TreeNode traversal(List<Integer> inorder, List<Integer> postorder) {if (postorder.size() == 0) return null;// 后序遍历数组最后一个元素,就是当前的中间节点int rootValue = postorder.get(postorder.size() - 1);TreeNode root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder.get(delimiterIndex) == rootValue) break;}// 切割中序数组List<Integer> leftInorder = new ArrayList<>(inorder.subList(0, delimiterIndex));List<Integer> rightInorder = new ArrayList<>(inorder.subList(delimiterIndex + 1, inorder.size()));// postorder 舍弃末尾元素postorder.remove(postorder.size() - 1);// 切割后序数组List<Integer> leftPostorder = new ArrayList<>(postorder.subList(0, leftInorder.size()));List<Integer> rightPostorder = new ArrayList<>(postorder.subList(leftInorder.size(), postorder.size()));root.left = traversal(leftInorder, leftPostorder);root.right = traversal(rightInorder, rightPostorder);return root;}public TreeNode buildTree(List<Integer> inorder, List<Integer> postorder) {if (inorder.size() == 0 || postorder.size() == 0) return null;return traversal(inorder, postorder);}
}
3.复杂度分析
- 时间复杂度:尽管递归深度会影响栈的空间复杂度,但从时间复杂度的角度看,每个节点都会导致一次遍历操作和一次分割操作,总的时间复杂度与树中节点数量成正比,即O(n)。这里的n代表树中节点的总数。
- 空间复杂度:该算法的时间复杂度为O(n),空间复杂度在最坏情况下也是O(n),主要是由于递归调用栈的深度可能达到O(n)。在实际应用中,若二叉树较为平衡,空间复杂度可以视为O(log n)
相关文章:

Day21:Leetcode513.找树左下角的值 +112. 路径总和 113.路径总和ii + 106.从中序与后序遍历序列构造二叉树
LeetCode:513.找树左下角的值 解决方案: 1.思路 在遍历一个节点时,需要先把它的非空右子节点放入队列,然后再把它的非空左子节点放入队列,这样才能保证从右到左遍历每一层的节点。广度优先搜索所遍历的最后一个节点…...
)
Java数据结构和算法(B树)
前言 B树又叫平衡的多路搜索树;平衡的意思是又满足平衡二叉树的一些性质,左树大于右树; 多路意思是,可以多个结点,不再是像二叉树只有两个结点; 实现原理 B树是一种自平衡的搜索树,通常用于实…...

成为程序员后我都明白了什么?从入行到弃坑?
作为一个入行近10年的php程序员,真心感觉一切都才刚开始,对计算机,编程语言的理解也好,程序员中年危机也罢,之前都是听别人说的,真的自己到了这个水平,这个年龄才深刻体会到这其中的种种。 我一…...

python --创建固定字符串长度,先进先出
a 123def concatenate_within_limit(b, new_string):# 计算新字符串与a的长度之和a btotal_length len(a) len(new_string)# 如果长度超过1024,从前面删除足够的字符if total_length > 5:diff total_length - 5a a[diff:] new_string # 删除前diff个字符…...

容器化部署
目录 docker容器化部署 怎样使用Docker Compose或Kubernetes等容器编排工具来管理和扩展联邦学习系统 使用Docker Compose...

国产数据库TiDB的常用方法
TiDB的常用方法主要涉及安装配置、数据操作、性能调优以及监控和维护等方面。以下是对这些常用方法的归纳和介绍: 1. 安装与配置 安装TiDB:根据官方文档的指引,用户可以按照步骤进行TiDB的安装。配置TiDB:安装完成后,…...

基于DdddOcr通用验证码离线本地识别SDK搭建个人云打码接口Api
前言 最近介绍了一款免费的验证码识别网站,识别效率太低,考虑到ddddocr是开源的,决定搭建搭建一个,发现原作者sml2h3已经推出好久了,但是网上没有宝塔安装的教程,于是本次通过宝塔搭建属于自己的带带弟弟OCR通用验证码离线本地识别 原项目地址:https://github.com/sml2…...
2、xss-labs之level2
1、打开页面 2、传入xss代码 payload:<script>alert(xss)</script>,发现返回<script>alert(xss)</script> 3、分析原因 打开f12,没什么发现 看后端源码,在这form表单通过get获取keyword的值赋给$str&am…...
人才测评的应用:人才选拔,岗位晋升,面试招聘测评
人才测评自诞生以来,就被广泛应用在各大方面,不仅是我们熟悉的招聘上,还有其他考核和晋升,都会需要用到人才测评。不知道怎么招聘?或者不懂得如何实现人才晋升?都可以参考人才测评,利用它帮我们…...

前端面试题日常练-day33 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末。 在jQuery中,以下哪个选项用于在元素上绑定一个点击事件? a) click() b) bind() c) on() d) trigger() jQuery中,以下哪个选项用于获取元素的属性值? …...

非整数倍数据位宽转换24to128
描述 实现数据位宽转换电路,实现24bit数据输入转换为128bit数据输出。其中,先到的数据应置于输出的高bit位。 电路的接口如下图所示。valid_in用来指示数据输入data_in的有效性,valid_out用来指示数据输出data_out的有效性;clk是时…...
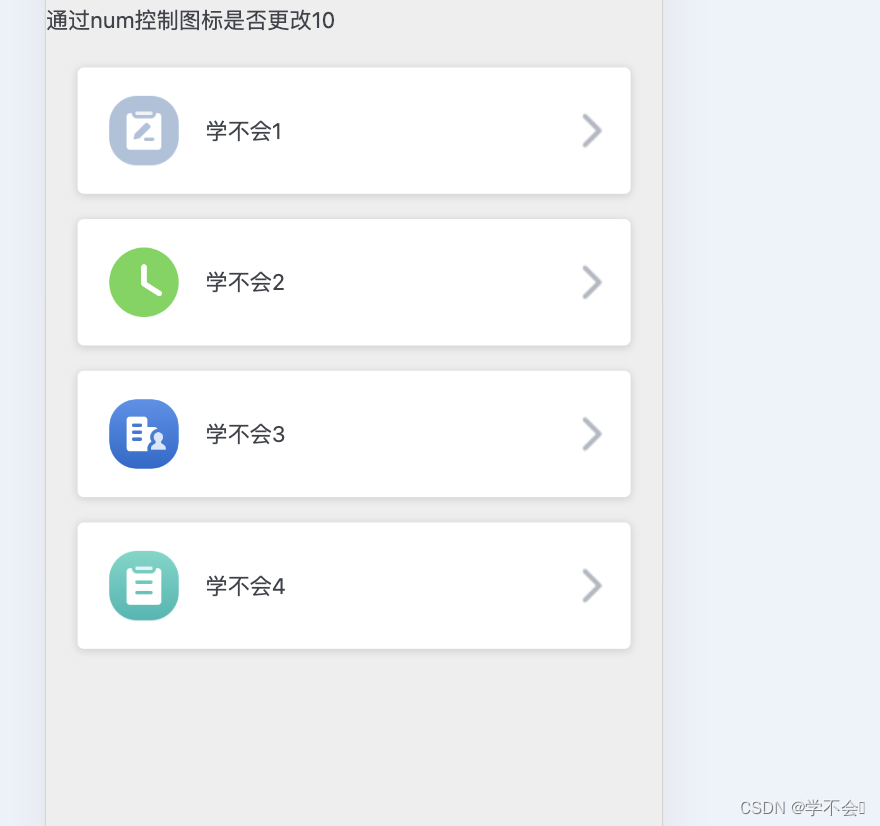
html通过数据改变,图片跟着改变
改变前 改变后 通过数据来控制样式展示 <template><div>通过num控制图标是否更改{{num}}<div class"box"><!-- 如果num大于1则是另一种,样式,如果小时1,则是另一种样式 --><div class"item&qu…...
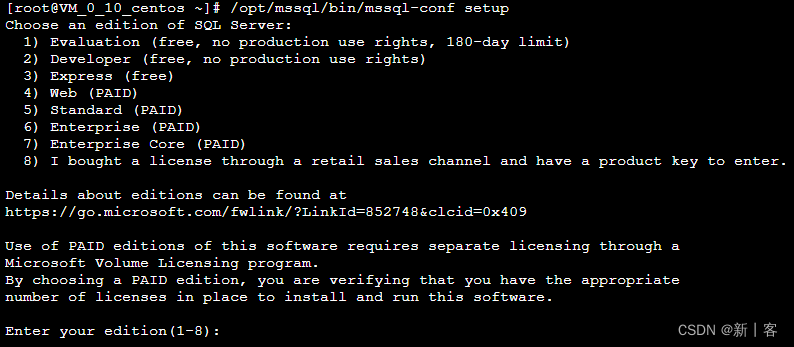
centos7.9 安装SqlServer
1、导入Microsoft SQL Server CentOS存储库: sudo curl -o /etc/yum.repos.d/mssql-server.repo https://packages.microsoft.com/config/rhel/7/mssql-server-2019.repo2、安装SQL Server: sudo yum install -y mssql-server假如机器内存不足2G 需要对…...

Idea中flume的Interceptor的编写教程
1.新建-项目-新建项目 注意位置是将来打包文件存放的位置,即我们打包好的文件在这/export/data个目录下寻找 2. 在maven项目中导入依赖 Pom.xml文件中写入 <dependencies> <dependency> <groupId>org.apache.flume</groupId> <artifa…...

java单元测试:JUnit测试运行器
JUnit测试运行器(Test Runner)决定了JUnit如何执行测试。JUnit有多个测试运行器,每个运行器都有特定的功能和用途。 1. 默认运行器 当没有显式指定运行器时,JUnit会使用默认运行器,这在JUnit 4和JUnit 5之间有所不同…...
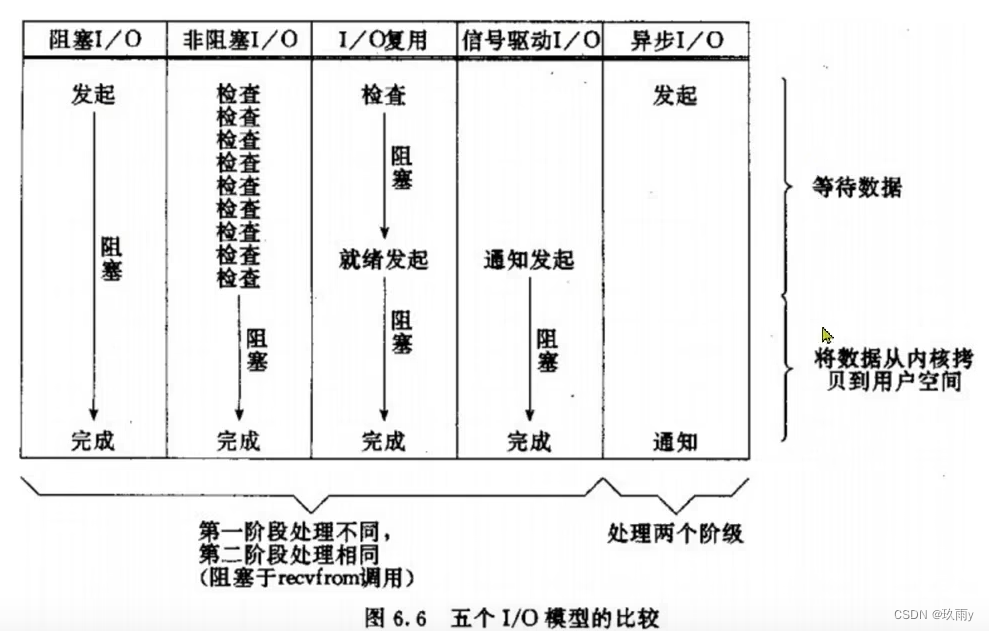
网络模型—BIO、NIO、IO多路复用、信号驱动IO、异步IO
一、用户空间和内核空间 以Linux系统为例,ubuntu和CentOS是Linux的两种比较常见的发行版,任何Linux发行版,其系统内核都是Linux。我们在发行版上操作应用,如Redis、Mysql等其实是无法直接执行访问计算机硬件(如cpu,内存…...
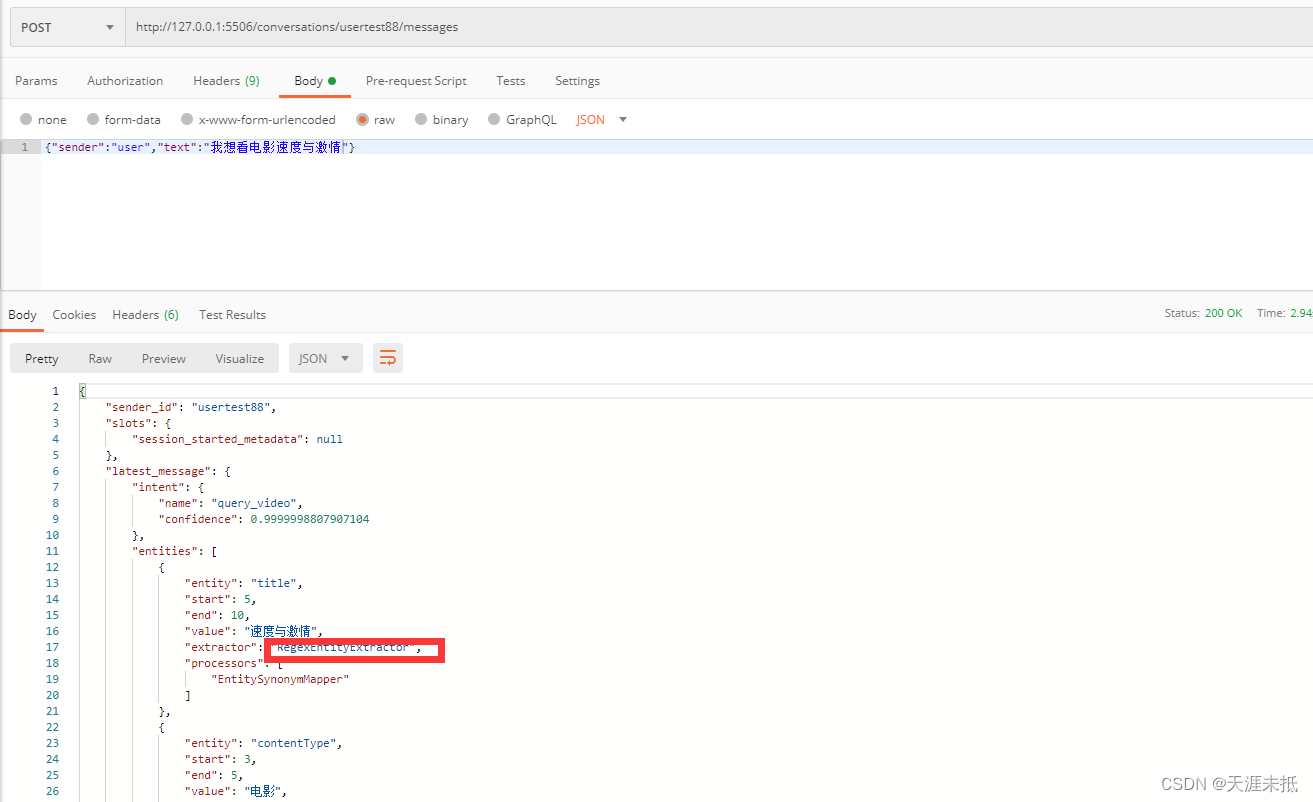
智能语义识别电影机器人的rasa实现
文章目录 0.前言1.项目整体框架2.rasa训练数据结构4.rasa启动命令及用到的API 0.前言 最近做了一个智能电影机器人的项目,我主要负责用户语义意图识别,用的框架是rasa,对应的版本为 3.6.15,对应的安装命令为: pip3 install rasa…...

C# 实现腾讯云 IM 常用 REST API 之会话管理
目录 关于腾讯 IM REST API 开发前准备 范例运行环境 常用会话管理API 查询账号会话总未读数 查询单聊会话消息记录 下载最近会话记录 小结 关于腾讯 IM REST API REST API 是腾讯即时通信 IM 提供给服务端的一组 HTTP 后台管理接口,如消息管理、群组管理…...

MySQL之Schema与数据类型优化(三)
Schema与数据类型优化 BLOB和TEXT类型 BLOB和TEXT都是为存储很大的数据而设计的字符串数据类型,分别采用二进制和字符方式存储。 实际上它们分别属于两组不同的数据类型家族:字符类型是TINYTEXT,SMALLTEXT,TEXT,MEDIUMTEXT,LONG…...

大语言模型发展历史
大语言模型的发展历史可以追溯到自然语言处理(NLP)和机器学习早期的探索,但真正快速发展起来是在深度学习技术兴起之后。以下是大语言模型发展的一个简要历史概述: 早期阶段(20世纪50-90年代): …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
