【对角线遍历】python

没啥思路


class Solution:def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:m=len(mat)n=len(mat[0])ret=[]if len(mat)==0:return retcount=0#m+n-1是对角线总数while count<m+n-1:#x和y的和刚好是count数#偶数为右上走if count%2==0:x=count if(count<m)else (m-1)y=count-xwhile(x>=0 and y<=n-1):ret.append(mat[x][y])x-=1y+=1#奇数左下走else:y=count if(count<n)else(n-1)x=count-ywhile(x<=m-1 and y>=0):ret.append(mat[x][y])x+=1y-=1count+=1return ret相关文章:

【对角线遍历】python
没啥思路 class Solution:def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:mlen(mat)nlen(mat[0])ret[]if len(mat)0:return retcount0#mn-1是对角线总数while count<mn-1:#x和y的和刚好是count数#偶数为右上走if count%20:xcount if(count<m)else (…...

温度检测小系统兼继电器模块和小风扇
1.思路: 代码还要封装! 延迟1秒;串口初始化;LCD1602显示屏初始化;延迟两秒;ledone不亮; while循环,延迟1秒,DHT模块读取数据;封装接收数据函数;发…...

[数据结构1.0]计数排序
读者老爷好,本鼠鼠最近学了计数排序,浅浅介绍一下! 目录 1.统计相同元素出现次数 2.根据统计的结果将序列回填到原来的序列中 3.相对映射计数排序 计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用,是非比较排…...

PostgreSQL入门教程
PostgreSQL是一种开源的关系型数据库管理系统,它具有高度的可靠性、可扩展性和性能。下面是一个简单的PostgreSQL入门教程,帮助你开始使用这个强大的数据库管理系统。 步骤1:安装PostgreSQL 首先,你需要下载并安装PostgreSQL。你…...

【spring】@ControllerAdvice注解学习
ControllerAdvice介绍 ControllerAdvice 是 Spring 框架提供的一个注解,用于定义一个全局的异常处理类或者说是控制器增强类(controller advice class)。这个特性特别适用于那些你想应用于整个应用程序中多个控制器的共有行为,比…...
【全开源】赛事报名系统源码(Fastadmin+ThinkPHP和Uniapp)
基于FastadminThinkPHP和Uniapp开发的赛事报名系统,包含个人报名和团队报名、成绩查询、成绩证书等。 构建高效便捷的赛事参与平台 一、引言:赛事报名系统的重要性 在举办各类赛事时,一个高效便捷的报名系统对于组织者和参与者来说都至关重…...
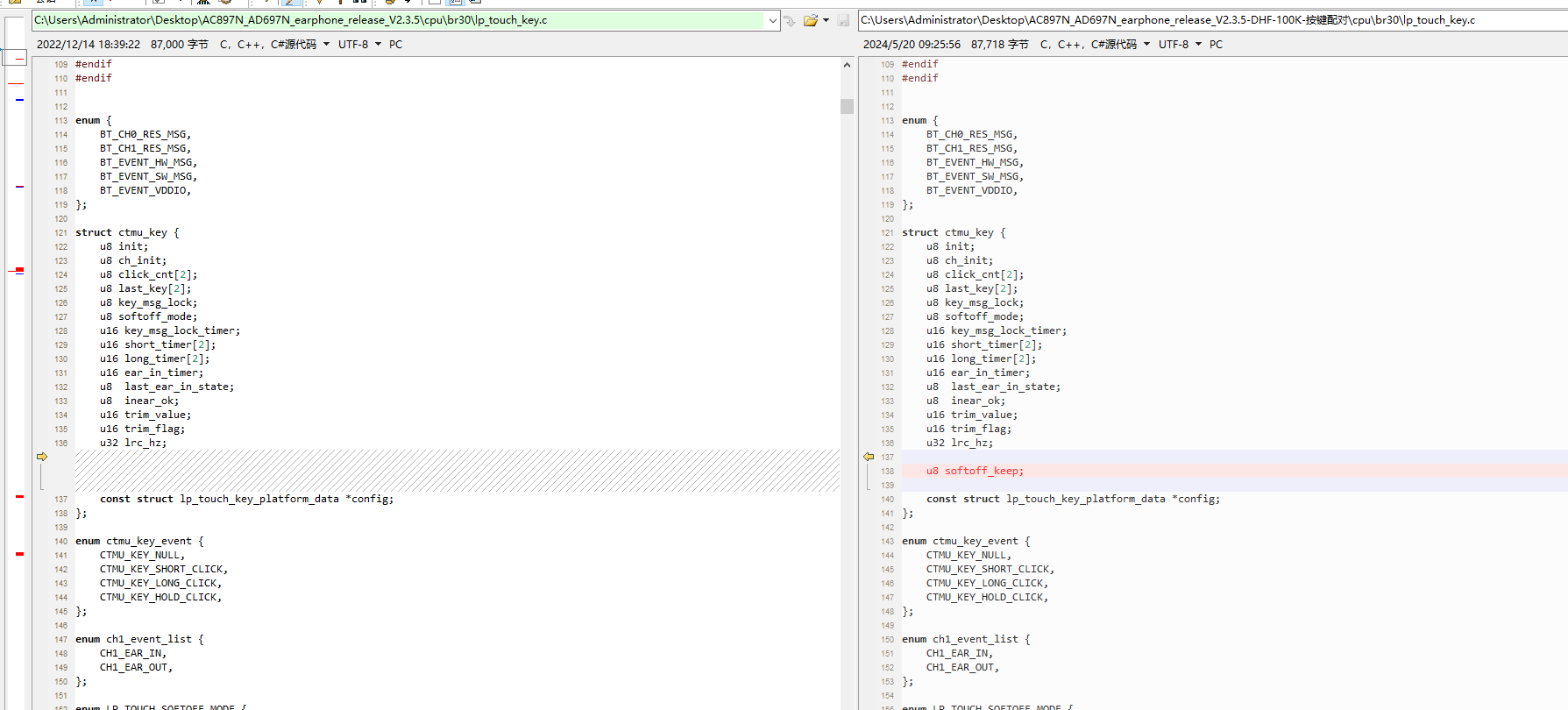
杰理-耳机进入关机关闭内内置触摸-节省功耗
杰理-耳机进入关机关闭内内置触摸-节省功耗 if (__this->init 0) {return LP_TOUCH_SOFTOFF_MODE_LEGACY; }if ((__this -> softoff_mode LP_TOUCH_SOFTOFF_MODE_ADVANCE) && (__this->softoff_keep 0)) {lp_touch_key_disable(); } __this->softoff_k…...

Homebrew安装、 Mac上pyenv的安装与使用,复制黏贴搞定,网上教程看得眼花缭乱的来看看,简单明了一步到胃!!
安装 Homebrew /bin/bash -c "$(curl -fsSL https://gitee.com/ineo6/homebrew-install/raw/master/install.sh)"安装pyenv brew install pyenv添加到终端使用的配置文件.zshrc、.bashrc 避免不必要的麻烦两个终端的配置文件都进行添加,文件在当前用户目…...
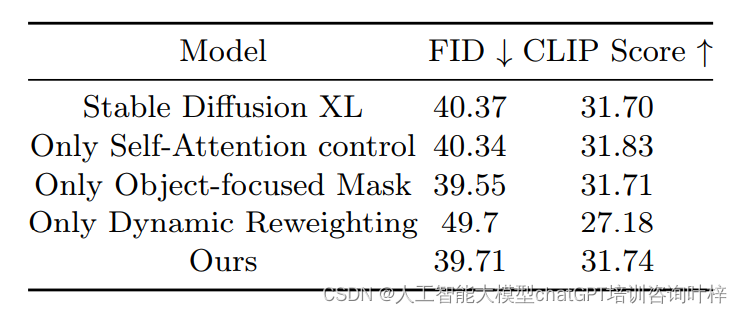
通过注意力调节实现更好的文本到图像生成对齐
近年来,生成性AI技术在众多领域取得了前所未有的进步。大规模预训练模型的出现激发了各种下游任务中的新应用。这在文本到图像生成领域尤为明显,例如Stable Diffusion、DALL-E 2和Imagen等模型已经显著展示了它们的能力。尽管如此,复杂提示中…...

Java开发大厂面试第26讲:生产环境如何排查问题和优化 JVM?
通过前面几个课时的学习,相信你对 JVM 的理论及实践等相关知识有了一个大体的印象。而本课时将重点讲解 JVM 的排查与优化,这样就会对 JVM 的知识点有一个完整的认识,从而可以更好地应用于实际工作或者面试了。 我们本课时的面试题是&#x…...

计算机科学的先驱者们
1. 艾伦图灵(Alan Turing): 图灵是计算机科学和人工智能的先驱之一,他提出了“图灵机”的概念,这是一种理论上的计算模型,奠定了现代计算机理论的基础。在第二次世界大战期间,图灵领导了一个团…...

哈希双指针
文章目录 一、哈希1.1两数之和1.2字母异位词分组1.3最长子序列 二、双指针2.1[移动零](https://leetcode.cn/problems/move-zeroes/description/?envTypestudy-plan-v2&envIdtop-100-liked)2.2[盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/d…...
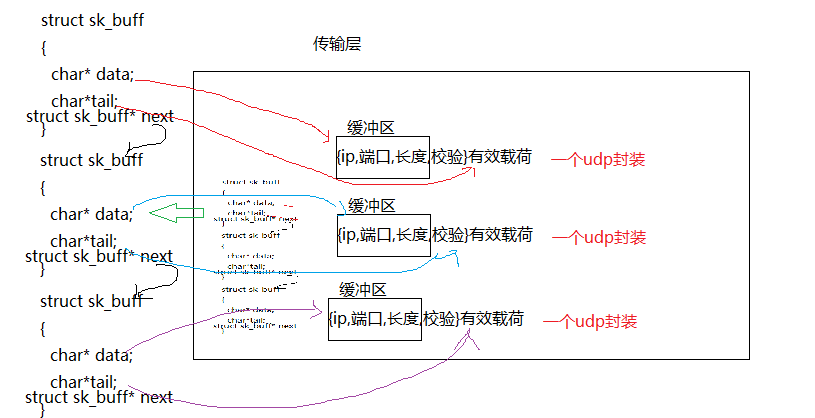
【网络】UDP协议
应用层协议是请求与响应服务,客户端的请求与服务器的响应是通过应用层传输到网络中的,但再实际上,应用层并不能直接通信,需要将数据进行报头的封装,向下层交付,贯穿整个协议栈。我们已经谈到应用层协议负责…...

牛马真的沉默了,入职第一天就干活
入职第一天就干活的,就问还有谁,搬来一台N手电脑,第一分钟开机,第二分钟派活,第三分钟干活,巴适。。。。。。 打开代码发现问题不断 读取配置文件居然读取两个配置文件,一个读一点,…...

解决在cmd里下载的库,但IDLE还是显示不存在的问题
原因一: 环境变量配置 首先,你需要确认你安装库的时候使用的Python环境是否和IDLE使用的Python环境是同一个。如果cmd中你使用的是系统路径下的Python,而IDLE使用的是另一个路径下的Python,那么你在cmd中下载的库,IDL…...

嵌入式全栈开发学习笔记---C语言笔试复习大全23
目录 联合体 联合体的定义 联合体的长度 如果来判断设备的字节序? 如何把大端数据转换成小端数据? 枚举 枚举的定义 上一篇复习了结构体,这一节复习联合体和枚举。 说明:我们学过单片机的一般都是有C语言基础的了ÿ…...

C++函数指针,键值对集合的学习
这段代码使用了 std::unordered_map 来存储 std::wstring 作为键(key),而对应的值(value)是一个 std::function<void(std::array<int, 5>, SomeClass&, int)> 类型的函数指针。这个结构使得根据字符串…...
新人攻略:避开这3大坑,让老员工主动带你飞!
进入职场的新人们,常常会感到困惑和挑战。他们可能会发现自己在与老员工的交流中遇到难题,甚至发现老员工并不愿意花费时间和精力去指导他们。这背后的原因是什么呢?又该如何改善这一现象呢?本文将从新员工的角度出发,…...

汽车液态电池隔膜的作用
标签: 汽车液态电池隔膜的作用; 聚乙烯(PE);聚丙烯(PP) 问题:汽车液态电池隔膜的作用? 汽车液态电池隔膜的作用 汽车液态电池中的隔膜是一个至关重要的组件,它在电池的性能、安全性和寿命方面起着关键作用。下面详细讲述隔膜的主要功能和作用: 1. 电化学隔离 隔…...

汽车液态电池充电时,充电时的化学反应是怎样的? 电池电量是怎么充满的?
标签: 汽车液态电池充电时的化学反应; 电池充电过程;锂电池,石墨负极 问题:汽车液态电池充电时,充电时的化学反应是怎样的? 电池电量是怎么充满的? 汽车液态电池充电时的化学反应 汽车液态电池(如锂离子电池)在充电时,通过电化学反应将电能转化为化学能并储存在电…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
