定积分求解过程是否变限问题 以及当换元时注意事项
目录
定积分求解过程是否变限问题
文字理解:
实例理解:
易错点和易混点:
1:定积分中的换元指什么?
2: 不定积分中第一类换元法和第二类换元法的本质和区别
3: df(x) ----> df(x)这个过程对大家产生困扰
换元时注意事项:
1:换元必换限,同时要将 dx = f(t)dt 也更换
2:换元要判断新元要保证连续可导:
3:积分区间上单调的替换函数是必要的
4:偶次方根下开平方,要加绝对值
5:牛顿莱布尼茨公式只适用于定积分,当定积分区间内有瑕点(该点的函数值为无穷)
定积分求解过程是否变限问题
文字理解:
定积分换元有一个口诀:换字必换限(所以不换字就不换限)。
理解:通过判断是否 引入一个新的变量替换原来的变量 来确定是否更换 积分限
白话理解:你在积分中,如果一直用字母t,那么那个积分限当然还是t等于多少的积分限。但是一旦你在积分中,不要原来的字母t了,换成一个新的字母x,那么积分限当然要换成x等于多少了?。这就叫做,这就叫做换字必换限。不换字就不换限。明白了没有?
实例理解:

来源:(1 封私信) 闲敲棋子落灯hua - 知乎 (zhihu.com)
(1 封私信) 龚漫奇 - 知乎 (zhihu.com)
易错点和易混点:
1:定积分中的换元指什么?
定积分中说的"换元"指的是引入新变量替换原变量
2: 不定积分中第一类换元法和第二类换元法的本质和区别
第一类换元法(凑微分):
第二类换元法:

通过这两个概念的引入,我们能清晰的认识到,第二类换元法的概念 与 定积分的换元的概念 是一 一对应的,故第二类换元法需要更换积分上下限。而第一类换元法的概念 与 定积分的换元的概念 并不是相同概念,故凑微分并不用更换积分上下限。
3: df(x) ----> df(x) 这个过程使大家产生困扰
定积分公式
当凑微分时会产生这样的过程 df(x) ----> df(x) 容易误导大家,让大家误以为是更换了积分变量,其实如果单单只是df(x) ----> dg(x) ,而u(x)对应的函数并未更换变量,此时并不表示更换积分变量。注 dx 也是 df(x)中的一种情况 当f(x) =x 时。
若:定积分公式 中 u(x)df(x) 经过一系类变化转换为 v(x)dg(x) 这个过程仍然并没有引入新的变量,变量仍是"x",不用更改积分限。刚好凑微分符合该条件,故凑微分不用修改积分上下限。
若:定积分公式 中u(x)df(x)经过一系列变换转换为v(t)dg(t)此时要根据变换过程及时更换积分上下限。第二类换元需要修改上下限。
注:一定要分清 凑微分法 和 第二类换元法 和 定积分的换元 在概念上的区别。
换元时注意事项:
1:换元必换限,同时要将 dx = f(t)dt 也更换
2:换元要判断新元要保证连续可导:
例如原积分区间(-1,1),换元函数是 x = 1/t ,很明显当x = 0时 t是无穷,所有新元函数在0处为无穷间断点,不连续也不可导,故此时不能换元。
3:积分区间上单调的替换函数是必要的
进行定积分的变量替换时,选择在积分区间上单调的替换函数是非常重要的。这可以确保替换过程中的一一对应性,避免积分上下限混淆,并简化积分计算过程。在实际操作中,务必检查替换函数的单调性和可逆性,以确保积分计算的正确性
4:偶次方根下开平方,要加绝对值
换元后,很多情况下都是会出现平方项,特别是三角换元,当遇见偶次根号下开方一定要小心
5:牛顿莱布尼茨公式只适用于定积分,当定积分区间内有瑕点(该点的函数值为无穷)
这个很少见,一般让你求定积分都是已经帮你筛选过瑕点区间不用很担心。除非题目问你:该积分是否能用牛顿莱布尼茨求。
相关文章:
定积分求解过程是否变限问题 以及当换元时注意事项
目录 定积分求解过程是否变限问题 文字理解: 实例理解: 易错点和易混点: 1:定积分中的换元指什么? 2: 不定积分中第一类换元法和第二类换元法的本质和区别 3: df(x) ----> df(x)这…...
)
保研机试算法训练个人记录笔记(七)
输入格式: 在第1 行给出不超过10^5 的正整数N, 即参赛}人数。随后N 行,每行给出一位参赛者的 信息和成绩,包括其所代表的学校的编号(从1 开始连续编号)及其比赛成绩(百分制)…...
-查询优化(23)-避免全表扫描)
【MySQL精通之路】SQL优化(1)-查询优化(23)-避免全表扫描
当MySQL使用全表扫描来解析查询时,EXPLAIN的输出在type列中显示ALL。 这种情况通常发生在以下情况下: 该表非常小,因此执行全表扫描比查找关键字更快。这对于少于10行且行长较短的表来说很常见。 对于索引列,ON或WHERE子句中没有…...
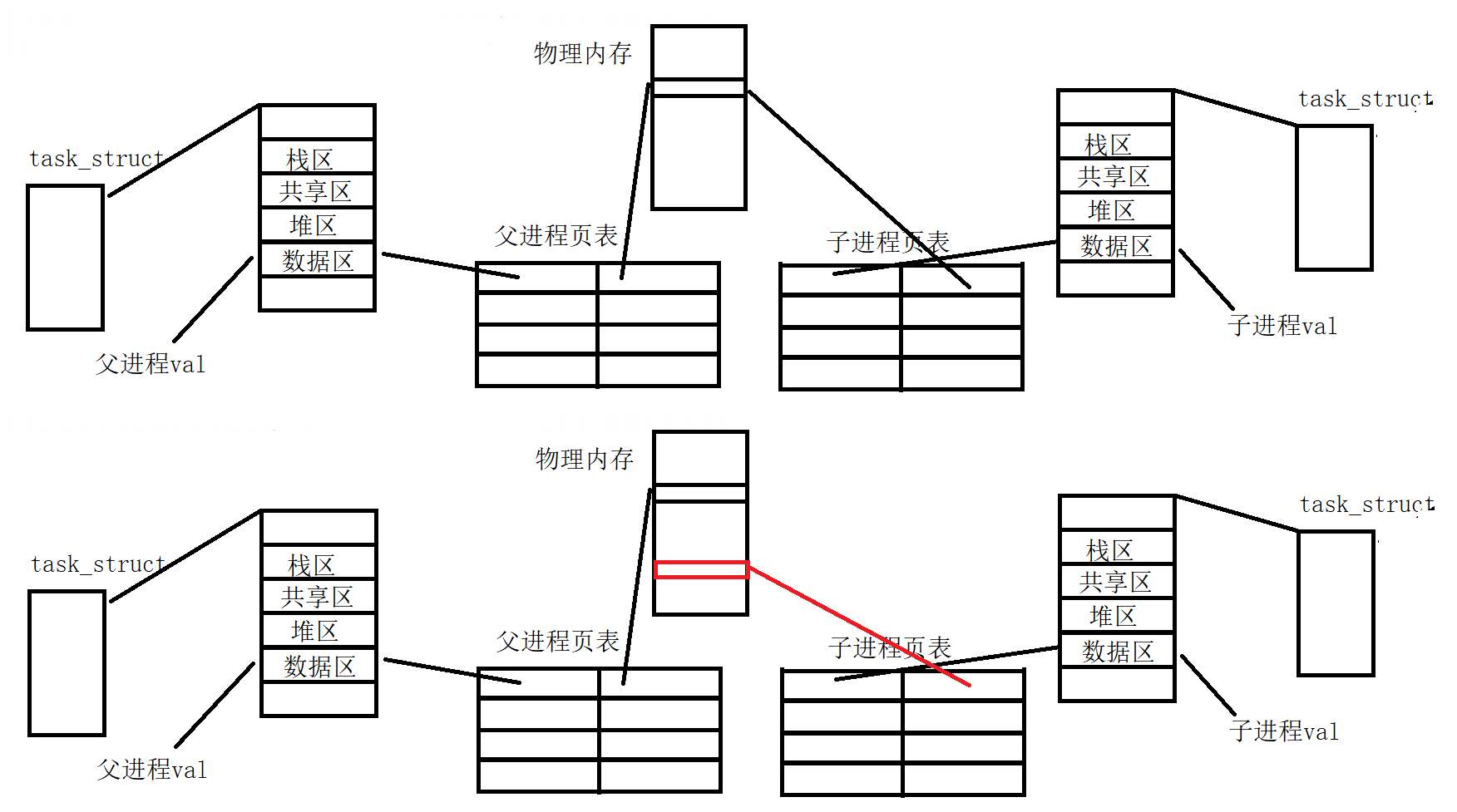
【Linux】写时拷贝技术COW (copy-on-write)
文章目录 Linux写时拷贝技术(copy-on-write)进程的概念进程的定义进程和程序的区别PCB的内部构成 程序是如何被加载变成进程的?写时复制(Copy-On-Write, COW)写时复制机制的原理写时拷贝的场景 fork与COWvfork与fork Linux写时拷贝技术(copy-…...

用python使用主成分分析数据
import pandas as pd #导入处理二维表格的库 import numpy as np #导入数值计算的库 from sklearn.preprocessing import StandardScaler #导入数据标准化模块 import matplotlib.pyplot as plt #导入画图的包 from sklearn.decomposition import PCA #导入主成…...

用WPS将多张图片生成一个pdf文档,注意参数设置
目录 1 新建一个docx格式的文档 2 向文档中插入图片 3 设置页边距 4 设置图片大小 5 导出为pdf格式 需要把十几张图片合并为一个pdf文件,本以为很简单,迅速从网上找到两个号称免费的在线工具,结果浪费了好几分钟时间,发现需要…...
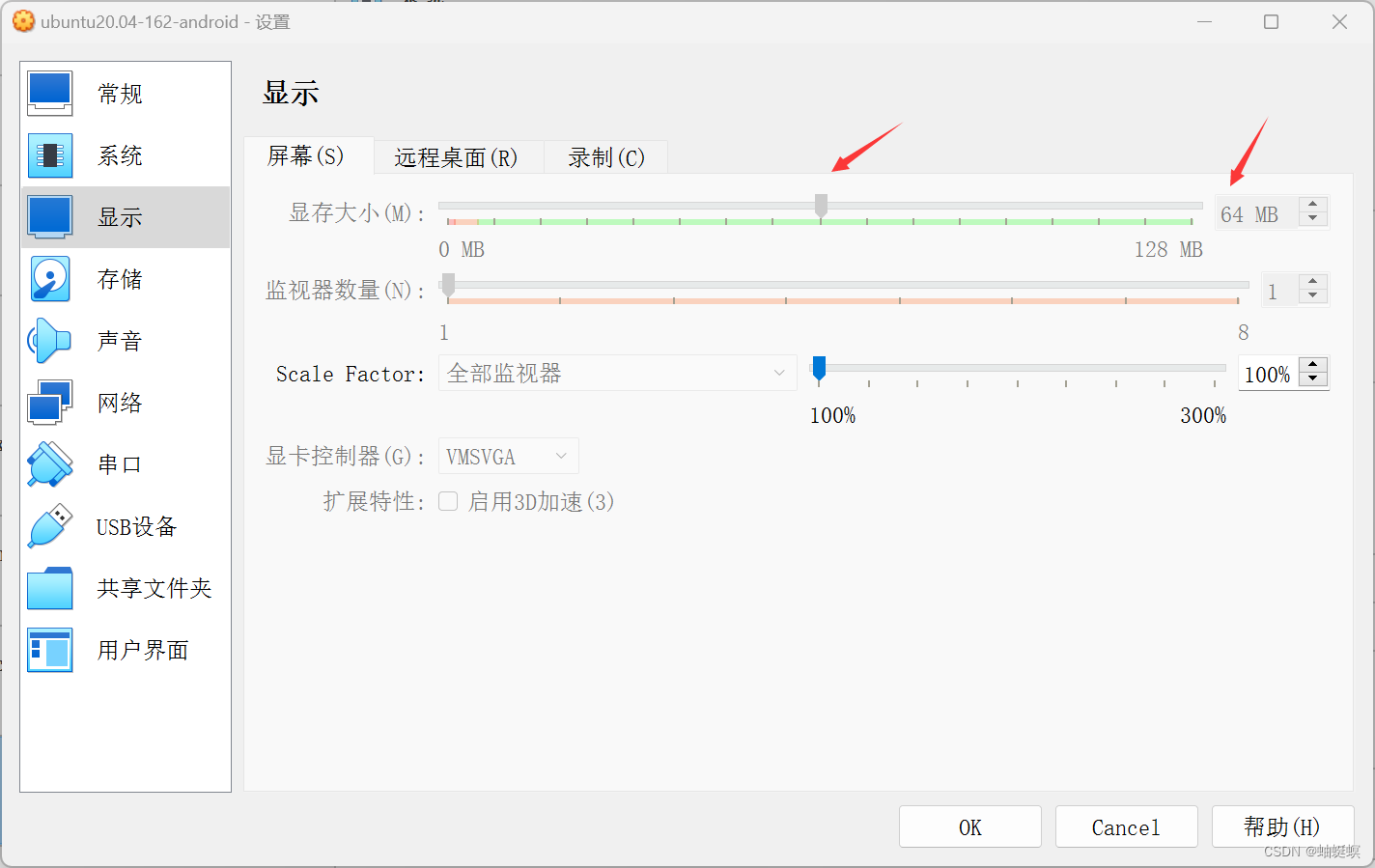
virtual box ubuntu20 全屏展示
virtual box 虚拟机 ubuntu20 系统 全屏展示 ubuntu20.04 视图-自动调整窗口大小 视图-自动调整显示尺寸 系统黑屏解决 ##设备-安装增强功能 ##进入终端 ##终端打不开,解决方案-传送门ubuntu Open in Terminal打不开终端解决方案-CSDN博客 ##点击cd盘按钮进入文…...
的使用)
react中的数据驱动视图,useState()的使用
前端开发如今有一个很重要的思想就是数据驱动视图,数据发生变化使ui发生变化,比如一个变量count,为0显示三个按钮,为1显示一个按钮,为2显示两个按钮。这就是一个简单的数据驱动视图。 import { useState } from reactf…...

金融数据库,实时行情,股票财务数据在线查询
jvQuant在线SQL 文档(current)接入 测试 查询 #股票代码股票简称最新价(元)2024-05-21股东总户数(户)截至2024-05-21上市板块是否ST股票区间涨跌幅(%)2024-05-15-2024-05-21市盈率(TTM)(倍)2024-05-21营业收入(元)截至2024-03-31总市值(元)2024-05-21量比2024-05-21利润率(%…...
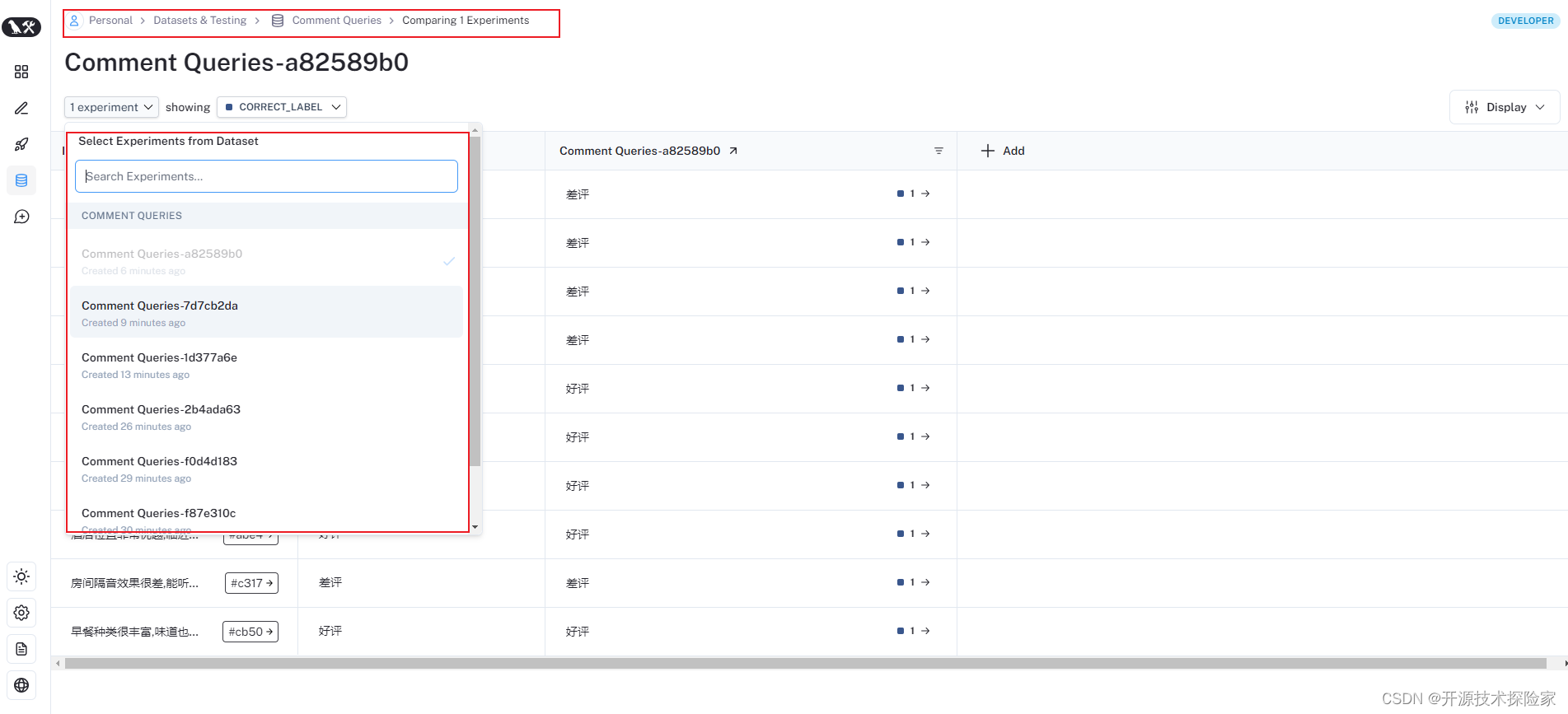
开源模型应用落地-LangSmith试炼-入门初体验-数据集评估(三)
一、前言 LangSmith是一个用于构建生产级 LLM 应用程序的平台,它提供了调试、测试、评估和监控基于任何 LLM 框架构建的链和智能代理的功能,并能与LangChain无缝集成。通过使用LangSmith帮助开发者深入了解模型在不同场景下的表现,让开发者能…...

设计模式 15 Decorator Pattern 装饰器模式
设计模式 15 Decorator Pattern 装饰器模式 1.定义 Decorator Pattern 装饰器模式是一种结构型设计模式,它允许在运行时给对象添加新的行为或职责,而无需修改对象的源代码。这种模式通过创建一个包装对象,也称为装饰器,来包裹原…...

cuda11.8安装torch2.0.1
pip install torch2.0.1 torchvision0.15.2 torchaudio2.0.2 --index-url https://download.pytorch.org/whl/cu118...

新手困 ViewModel与Activting的databinding2个对象 区别
在Android开发中,ViewModel与Activity的Binding并不是同一个概念,它们分别指的是不同的功能和用途。 ViewModel: ViewModel是一个为UI界面提供数据的类,它负责管理Activity或Fragment的数据。ViewModel类持有数据的引用,即使配置…...

Cocos Creator 声音播放与管理详解
Cocos Creator 是一款非常流行的游戏开发引擎,它提供了丰富的功能和工具,让开发者可以轻松构建出高质量的游戏。在游戏开发中,声音是一个非常重要的元素,可以为游戏增添氛围和趣味性。在本文中,我们将详细介绍Cocos Cr…...

今日早报 每日精选15条新闻简报 每天一分钟 知晓天下事 5月26日,星期日
每天一分钟,知晓天下事! 2024年5月26日 星期日 农历四月十九 1、 医保局:支持将符合条件的村卫生室纳入医保定点,方便农村居民就医。 2、 网传养老金储备严重不足?央视辟谣:这笔钱二十多年来从未动用过&a…...
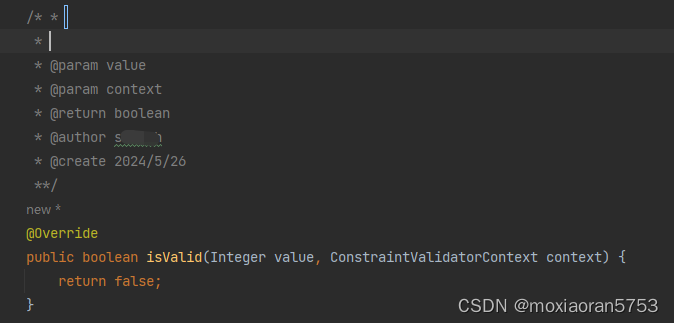
IDEA快速生成类注释和方法注释的方法
1.生成类、接口、枚举、注解等文件的注释,不仅仅是class 2.生成方法注释的 可在方法上方空行输入/** 按enter键快速生成。生成的样式如下: PS:生成的返回值带一堆英文文字说明,感觉没必要 如果想生成比较全面的方法注释,如作者&…...
业务模块之一对一聊天、添加好友函数、好友类以及离线消息类)
[集群聊天服务器]----(七)业务模块之一对一聊天、添加好友函数、好友类以及离线消息类
接着[集群聊天服务器]----(六)业务模块之用户注册、登录、退出以及客户端异常退出函数中对于业务模块的用户注册、登录、退出以及客户端异常退出函数的剖析,现在我们对点对点聊天以及添加好友的实现进行剖析。 点对点聊天 当客户端输入msgidONE_CHAT_MSG时&#x…...

java中使用jedis连接redis
4.java中使用jedis连接redis...
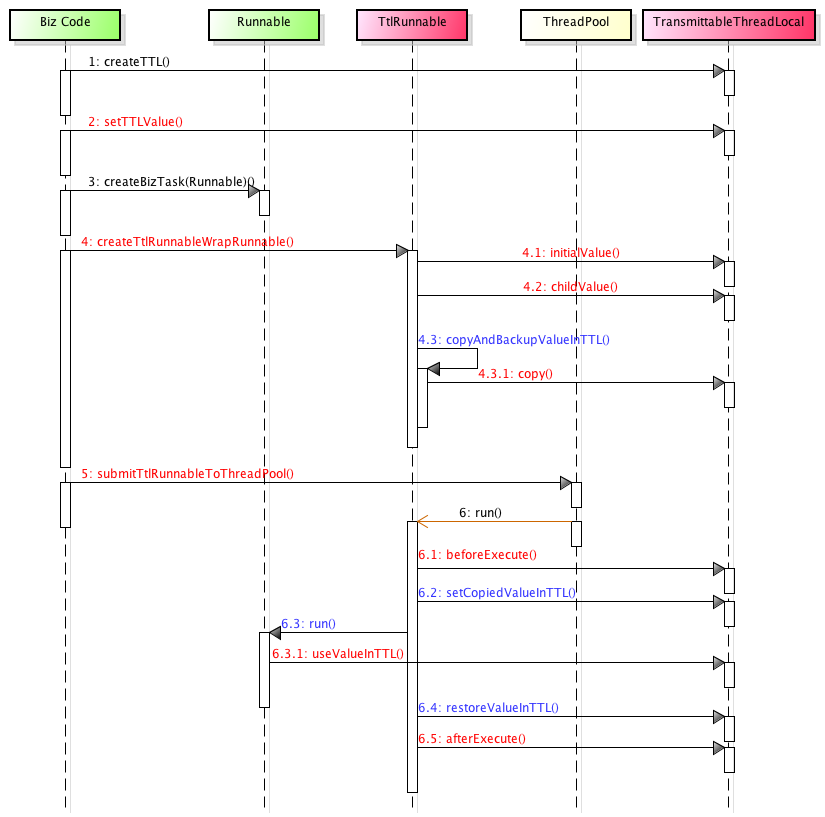
【多线程开发 2】从代码到实战TransmittableThreadLocal
【多线程开发 2】从代码到实战TransmittableThreadLocal 本文将从以下几个点讲解TransmittableThreadLocal(为了方便写以下简称ttl): 前身 是什么? 可以用来做什么? 源码原理 实战 前身 ThreadLocal 要了解ttl就要先了解Java自带的类…...

【车载以太网测试从入门到精通】——SOME/IP协议测试
系列文章目录 【车载以太网测试从入门到精通】系列文章目录汇总 文章目录 系列文章目录前言一、SOME/IP时间参数1.INITIAL_DELAY时间2.REPETITIONS_MAX次数3.REPETITIONS_BASE_DELAY时间4.CYCLIC_OFFER_DELAY时间5.TIME_TO_LIVE时间6.SUBSCRIBE_RETRY_DELAY时间二、SOME/IP服务…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
