数据结构~~链式二叉树
目录
一、基本概念
链式存储概念
二、链式二叉树的结构
链式二叉树结构
构建链式二叉树
二叉树的遍历
二叉树节点和高度等
二叉树销毁
三、链式二叉树的练习
相同的树
对称二叉树
另外一颗子树
二叉树前序遍历
二叉树遍历
四、完整代码
Tree.h
Tree.c
五、总结
一、基本概念
链式二叉树是一种常见的数据结构,它是用链表结点来存储二叉树中的每一个结点,结点结构通常包括数据域和若干个指针域。其中,指针域用于指向左孩子结点和右孩子结点。
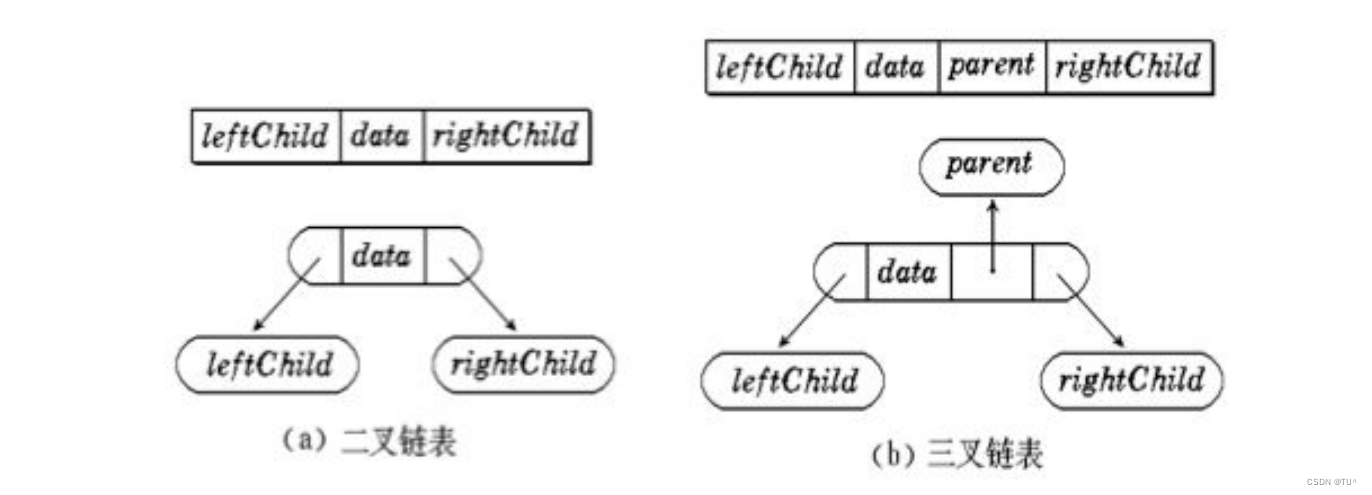
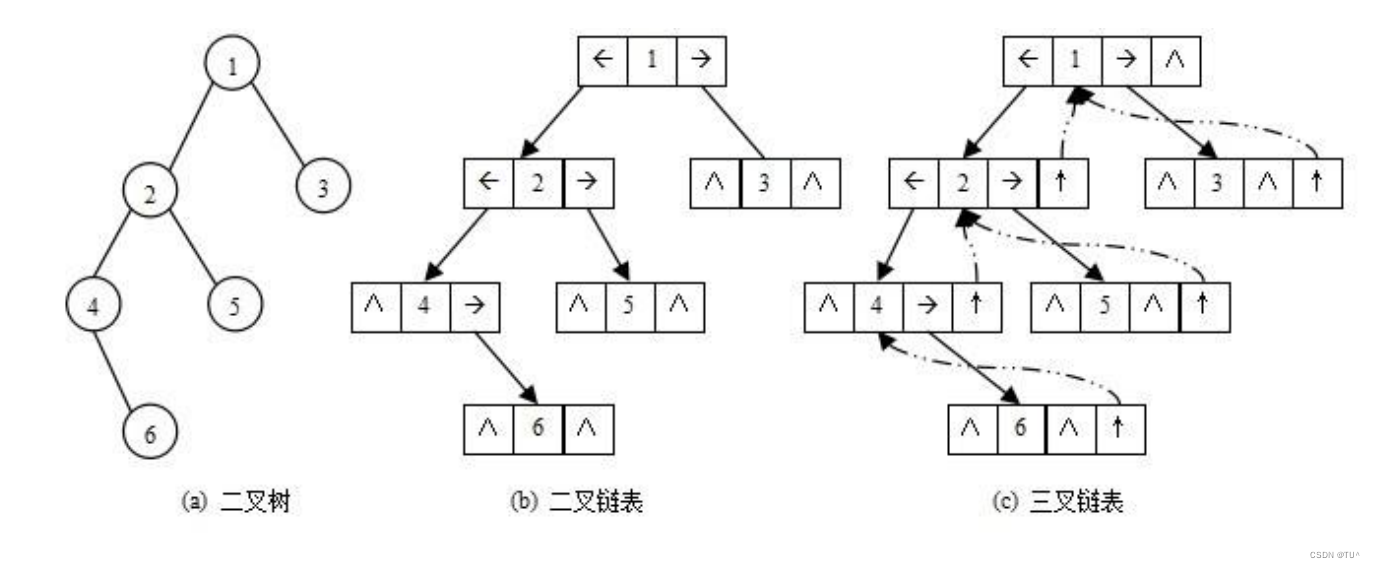
对于那些非完全二叉树,由于顺序存储结构的空间利用率低,因此二叉树一般都采用链式存储结构。在链式二叉树中,根据指针的数量可以分为二叉链和三叉链两种结构。二叉链的结点包含存储数据的变量、存储左孩子的指针以及存储右孩子的指针;而三叉链的结点除了包含存储数据的变量、存储左孩子的指针以及存储右孩子的指针,还包含存储双亲的指针。
二叉树的遍历是指按某条搜索路径访问树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。根据访问根结点的顺序不同可以分为前序遍历、中序遍历和后序遍历。
链式存储概念
链式存储二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链。
二、链式二叉树的结构
链式二叉树结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;构建链式二叉树
int类型 手撕构建方便前期调试
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc err");return NULL;}newnode->_data = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
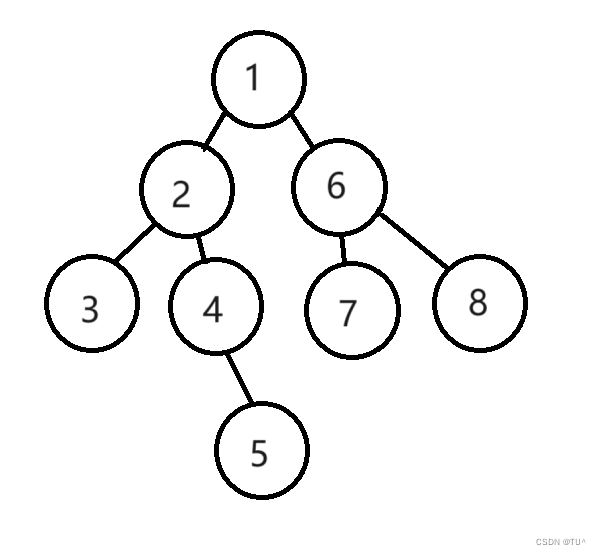
}//123nn4n5nn67nn8nn 通过前序遍历构建
BTNode* BinaryTreeCreate()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);BTNode* node8 = BuyNode(8);node1->_left = node2;node1->_right = node6;node2->_left = node3;node2->_right = node4;node4->_right = node5;node6->_left = node7;node6->_right = node8;return node1;
}char数组类型
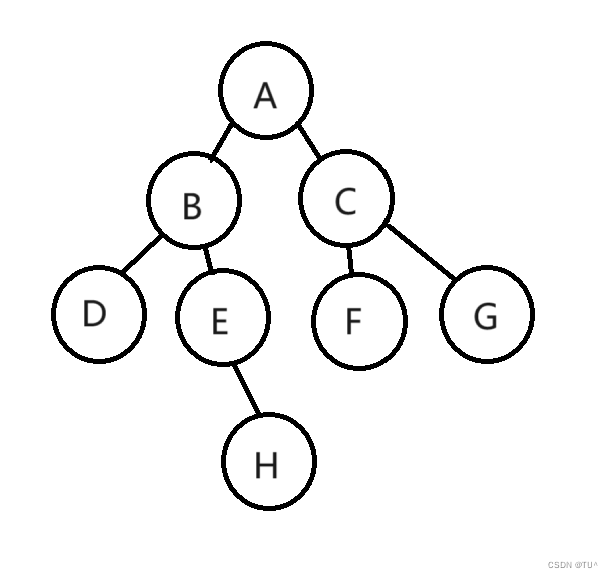
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreateChar(BTDataType* a, int* pi)
{if (a[(*pi)] == '#'){(*pi)++;return NULL;}BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc err");return NULL;}newnode->_data = a[(*pi)++];newnode->_left = BinaryTreeCreateChar(a, pi);newnode->_right = BinaryTreeCreateChar(a, pi);return newnode;
}二叉树的遍历
前序:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
前序遍历递归图解:
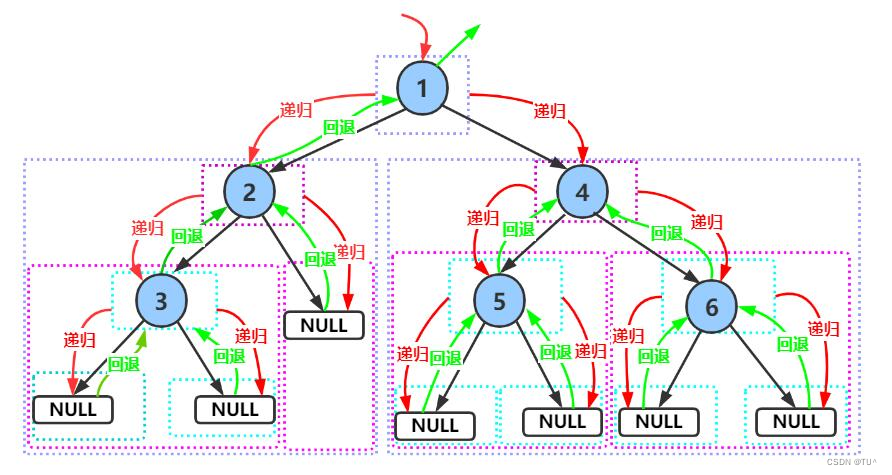
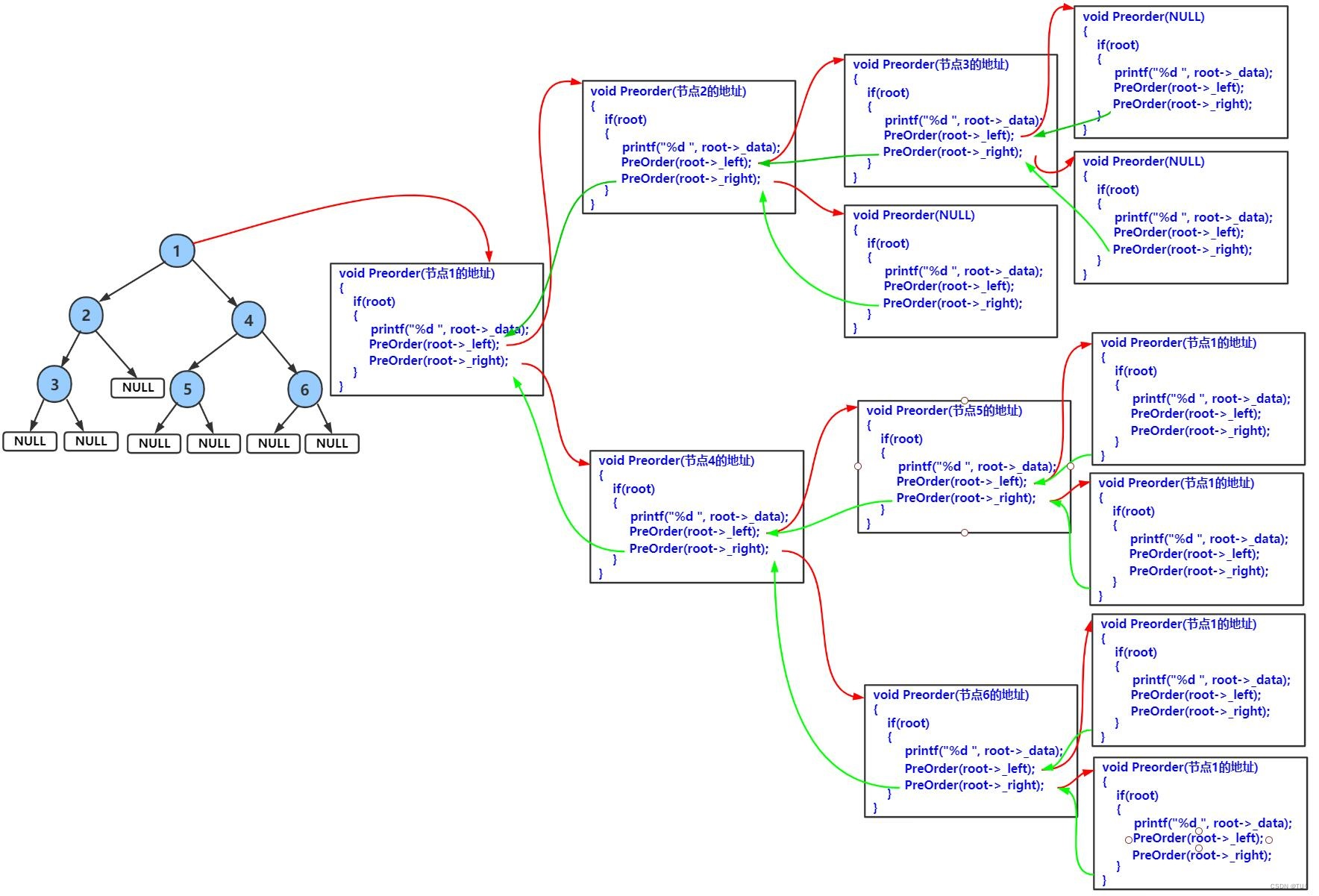
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}中序:中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->_left);printf("%d ",root->_data);BinaryTreeInOrder(root->_right);
}后序:后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ",root->_data);
}层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
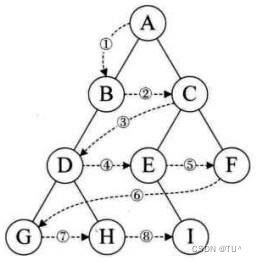
// 层序遍历
#include"Queue.h"
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);printf("%d ",Fout->_data);if (Fout->_left){QueuePush(&q,Fout->_left);}if (Fout->_right){QueuePush(&q, Fout->_right);}}QueueDestroy(&q);
}判断二叉树是否是完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);if (Fout == NULL){break;}QueuePush(&q, Fout->_left);QueuePush(&q, Fout->_right);}while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);if (root){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}二叉树节点和高度等
1.二叉树节点个数
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_left)+1;
}
2.二叉树叶子节点个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left==NULL && root->_right==NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}3.二叉树的最大高度
//二叉树的最大高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int node_left=TreeHeight(root->_left); int node_right = TreeHeight(root->_right);return node_left > node_right ? node_left + 1 : node_right + 1;
}4.二叉树第k层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}5.二叉树查找值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2)return ret2;return NULL;}
二叉树销毁
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*(root) == NULL)return;BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*(root));
}三、链式二叉树的练习
相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
思路: 可以通过递归的方式同时遍历两棵树。
比较两棵树的根节点值是否相等,如果不相等则直接返回 false。
然后递归地对左子树和右子树分别进行相同的比较,只有当左右子树在相应位置上都相同的时候才返回 true。
在递归过程中,只要有一处不满足相同条件就可以立即返回 false,只有所有节点和结构都完全一致才能最终返回 true。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true;if (p == NULL || q == NULL)return false;if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right); }
对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
思路:
采用递归的方法。
一个二叉树是轴对称的,意味着对于任意一个节点,它的左子树和右子树是镜像对称的。
具体来说,就是对于当前节点,它的左子节点和右子节点的值相等(如果都存在的话),并且左子节点的左子树和右子节点的右子树对称,左子节点的右子树和右子节点的左子树也对称。我们通过递归地比较左右子树的对应节点来判断整个二叉树是否对称。如果在递归过程中发现不满足对称条件的情况,就可以返回 false,如果递归完整棵树都满足,则返回 true。
* Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool _isSymmetric(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true;if (p == NULL || q == NULL)return false;if (p->val != q->val)return false;return _isSymmetric(p->left, q->right)&&_isSymmetric(p->right, q->left); } bool isSymmetric(struct TreeNode* root) {return _isSymmetric(root->left, root->right); }
另外一颗子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
思路
我们可以从根节点开始,对主树 root 进行先序遍历。
在遍历过程中,每当遇到一个节点,就判断以这个节点为根的子树是否与 subRoot 完全相同。
为了判断子树是否相同,可以编写一个辅助函数来比较两棵树是否完全一致,这与前面判断两棵树是否相同的思路类似,即同时递归地检查节点值以及左右子树的结构和节点值是否匹配。如果找到匹配的子树,就返回 true,否则继续遍历主树的其他节点。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true;if (p == NULL || q == NULL)return false;if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right); } bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {if(root==NULL)return false;if( root->val==subRoot->val &&isSameTree(root,subRoot))return true;return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot); }
二叉树前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
思路:
首先访问根节点,然后递归地对左子树进行前序遍历,最后递归地对右子树进行前序遍历。
具体来说,我们可以使用一个辅助函数,在这个函数中先输出当前节点的值,然后如果左子树存在就对左子树调用该函数进行递归遍历,接着如果右子树存在就对右子树调用该函数进行递归遍历。这样就可以按照前序遍历的顺序输出所有节点的值。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ /*** Note: The returned array must be malloced, assume caller calls free().*/ int TreeSize(struct TreeNode* root) {return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; } void PrevOrder(struct TreeNode* root,int* a,int* i) {if(root==NULL)return;a[(*i)++]=root->val;PrevOrder(root->left,a,i);PrevOrder(root->right,a,i); } int* preorderTraversal(struct TreeNode* root, int* returnSize) {* returnSize=TreeSize(root);int* a=(int*)malloc(sizeof(int)*(*returnSize));int i = 0;PrevOrder(root,a,&i);return a; }
二叉树遍历
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
思路:
1. 定义二叉树节点结构体:包含节点值以及左右子节点指针。
2. 构建二叉树函数:通过遍历输入的先序遍历字符串来构建二叉树。使用一个静态索引来跟踪当前处理的字符位置。如果遇到非'#'字符,就创建一个新节点,然后递归地构建左子树和右子树,遇到'#'则表示空节点。
3. 中序遍历函数:按照中序遍历的顺序(先左子树、当前节点、再右子树)输出节点值并添加空格。
4. 在主程序中,获取用户输入的字符串,调用构建二叉树函数得到二叉树,然后调用中序遍历函数输出结果。
#include<stdio.h> #include<stdlib.h>typedef struct Tree {struct Tree* le;struct Tree* ri;int val; } BTNode;void PrevInor(BTNode* root) {if (root == NULL)return;PrevInor(root->le);printf("%c ", root->val);PrevInor(root->ri); }BTNode* BUTree(char* a,int* pi) {if(a[*pi] =='#'){(*pi)++;return NULL;}BTNode* newnode=(BTNode*)malloc(sizeof(BTNode));newnode->val=a[(*pi)++];newnode->le=BUTree(a, pi);newnode->ri=BUTree(a, pi);return newnode; } int main() {char a[100];scanf("%s",a);int i=0;BTNode* node=BUTree(a, &i);PrevInor(node); }
四、完整代码
Tree.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate();//BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
BTNode* BuyNode(BTDataType x);//求二叉树的最长高度
int TreeHeight(BTNode* root);Tree.c
#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc err");return NULL;}newnode->_data = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}/*int n,*/
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreateChar(BTDataType* a, int* pi)
{if (a[(*pi)] == '#'){(*pi)++;return NULL;}BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc err");return NULL;}newnode->_data = a[(*pi)++];newnode->_left = BinaryTreeCreateChar(a, pi);newnode->_right = BinaryTreeCreateChar(a, pi);return newnode;
}//123nn4n5nn67nn8nn
BTNode* BinaryTreeCreate()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);BTNode* node8 = BuyNode(8);node1->_left = node2;node1->_right = node6;node2->_left = node3;node2->_right = node4;node4->_right = node5;node6->_left = node7;node6->_right = node8;return node1;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*(root) == NULL)return;BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*(root));
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_left)+1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left==NULL && root->_right==NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2)return ret2;return NULL;}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->_left);printf("%d ",root->_data);BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ",root->_data);
}
// 层序遍历
#include"Queue.h"
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);printf("%d ",Fout->_data);if (Fout->_left){QueuePush(&q,Fout->_left);}if (Fout->_right){QueuePush(&q, Fout->_right);}}QueueDestroy(&q);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);if (Fout == NULL){break;}QueuePush(&q, Fout->_left);QueuePush(&q, Fout->_right);}while (!QueueEmpty(&q)){BTNode* Fout = QueueFront(&q);QueuePop(&q);if (root){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}//二叉树的最大高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int node_left=TreeHeight(root->_left); int node_right = TreeHeight(root->_right);return node_left > node_right ? node_left + 1 : node_right + 1;
}
Queue.c(部分)
void QueueInit(Queue* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}
void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc err");return;}newnode->data = x;newnode->next=NULL;if (pq->phead == NULL){assert(pq->ptail == NULL);pq->phead = pq->ptail= newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else {QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL&& pq->ptail == NULL;
}五、总结
二叉树全面总结:
定义:
二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。主要特点:
• 节点度最大为 2。
• 具有递归结构。
重要类型:
• 满二叉树:所有节点都有两个子节点,且叶子节点都在同一层。
• 完全二叉树:除了最后一层,其他层都是满的,最后一层的叶子节点靠左排列。
遍历方式:
• 前序遍历:先访问根节点,再遍历左子树,最后遍历右子树。
• 中序遍历:先遍历左子树,再访问根节点,最后遍历右子树。
• 后序遍历:先遍历左子树,再遍历右子树,最后访问根节点。
• 层次遍历:按照层次依次访问节点。
应用:
• 高效搜索和排序。
• 表达式树。
• 二叉堆实现优先队列等。
性质:
• 在完全二叉树中,节点编号与层次存在特定关系。
• 叶子节点数与度为 2 的节点数存在一定关系。
存储方式:
• 链式存储:通过节点指针连接。
• 数组存储:适用于完全二叉树。
常见算法:
• 构建二叉树。
• 求深度、高度。
• 查找节点。
• 平衡性判断及调整(如 AVL 树、红黑树等)。
二叉树是数据结构中的基础且重要部分,在计算机科学中有广泛的应用和研究价值。
相关文章:

数据结构~~链式二叉树
目录 一、基本概念 链式存储概念 二、链式二叉树的结构 链式二叉树结构 构建链式二叉树 二叉树的遍历 二叉树节点和高度等 二叉树销毁 三、链式二叉树的练习 相同的树 对称二叉树 另外一颗子树 二叉树前序遍历 二叉树遍历 四、完整代码 Tree.h Tree.c 五、总结 一…...
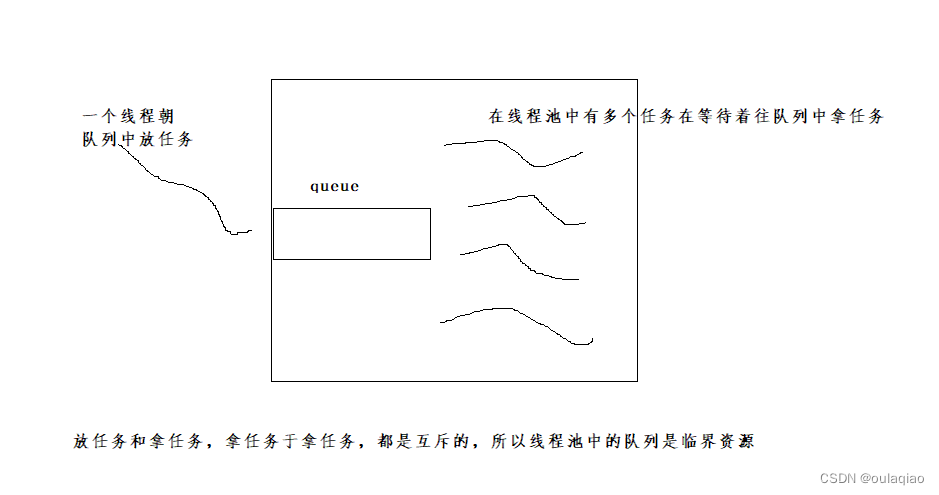
线程池,日志
所要用到的知识点: 多线程的创建 生产消费模型, 线程锁 条件变量 代码: 线程池日志...

vue的图片上传
关于vue3的图片上传,这里记录一下,有兴趣的朋友可以参考。。。。 <van-uploader:after-read"afterRead"v-model"headImg":max-count"1"class"picture"/> const fileList ref();const afterRead (fil…...

题解 P1150
题解 P1150 因为k个烟蒂1根烟1个烟蒂 所以k-1个烟蒂1根烟 注意减掉最后一根烟的烟蒂 (因这题并没有借烟蒂换烟再还回这一说) 此解法为小学4~6年级水平 #include <bits/stdc.h>using namespace std;int main(){int n,k;cin>>n>>k;cout<<n(n-1)/(k-…...

牛客NC324 下一个更大的数(三)【中等 双指针 Java/Go/PHP/C++】参考lintcode 52 · 下一个排列
题目 题目链接: https://www.nowcoder.com/practice/475da0d4e37a481bacf9a09b5a059199 思路 第一步:获取数字上每一个数,组成数组arr 第二步:利用“下一个排列” 问题解题方法来继续作答,步骤:利用lintc…...

Vue3解决“找不到模块“@/components/xxx.vue”或其相应的类型声明”
文章目录 前言背景问题描述解决方案总结 前言 在使用 Vue 3 开发项目时,遇到“找不到模块 ‘/components/xxx.vue’ 或其相应的类型声明”的错误是一个常见问题。这通常与 TypeScript 和模块解析相关的配置不当有关。本文将详细介绍如何解决此问题,确保…...

nginx的Connection refused
问题描述 nginx的错误日志中突然出现大量的的Connection refused问题,日志如下: 2020/03/19 09:52:53 [error] 20117#20117: *7403411764 connect() failed (111: Connection refused) while connecting to upstream, client: xxx.xxx.xxx.xxx, server:…...
)
Haskell 的高阶函数(Higher-order functions)
本节继续介绍Haskell的知识,本节内容介绍的是高阶函数(Higher-order functions)的概念和应用。高阶函数是指能够接受其他函数作为参数,或者返回函数作为结果的函数。 Functions as values(函数作为值)&…...

Unity websocket客户端
🏆 个人愚见,没事写写笔记 🏆《博客内容》:Unity3D开发内容 🏆🎉欢迎 👍点赞✍评论⭐收藏 🔎目标:服务器和客户端可以实时的传输信息 ☀️实现目标: 使用的w…...

每日一题——博弈论(枚举与暴力)
博弈论 题目描述 运行代码 #include<iostream> #include<vector> using namespace std; int main(){int n;cin >> n;vector<int> d(n,0);for(int i 0;i < n;i){cin >> d[i];}vector<int> in(1000,0);for(int k 1;k<3;k){for(int…...

pytorch笔记:torch.nn.Flatten()
1 介绍 torch.nn.Flatten(start_dim1, end_dim-1) 将一个连续的维度范围扁平化为一个张量 start_dim (int)要开始扁平化的第一个维度(默认值 1)end_dim (int)要结束扁平化的最后一个维度(默认值 -1) 2 举例 input torch.ra…...

一个人应该怎么操作抖音小店呢?店铺操作流程给你讲解清楚!
大家好,我是电商小V 现在入驻抖音小店的有很多新手,新手最关心的就是一个人应该如何操作抖音小店,操作抖音小店需要做好哪几步呢?关于这个问题咱们就来详细的讲解一下, 第一点:开店 开店是做店的第一步&…...

“等保测评与安全运维的协同:保障企业网络安宁
"等保测评与安全运维的协同:保障企业网络安宁"是一个涉及信息安全领域的重要话题。这里,我们可以从几个方面来探讨这个主题。 1. 等保测评(等级保护测评) 等保测评,即信息安全等级保护测评,是依…...

python抽取pdf中的参考文献
想将一份 pdf 论文中的所有参考文献都提取出来,去掉不必要的换行,放入一个 text 文件,方便复制。其引用是 ieee 格式的,形如: 想要只在引用序号(如 [3])前换行,其它换行都去掉&…...

Java进阶学习笔记21——泛型概念、泛型类、泛型接口
泛型: 定义类、接口、方法的时候,同时声明了一个或者多个类型变量(如: <E>),称之为泛型类、泛型接口、泛型方法,我们统称之为泛型。 说明这是一个泛型类。 如果不使用泛型,我们可以往ArrayList中传…...

第二天-⑦前后端需要注意的事项
①防xss跨站脚本攻击...
)
Socket 函数详细讲解(Socket编程步骤、socket函数、TCP和UDP的区别)
Socket 函数详细讲解和 C 示例 一、 Socket 基本概念1. Socket 简介2. Socket 编程步骤3. TCP Socket 编程示例服务器端客户端 4. 详细说明 二、 socket 函数1. domain 通讯的协议家族2. type 数据传输的类型3. protocol 最终使用的协议返回值示例 三、TCP 和 UDP的区别1. TCP&…...

【限免】杂波环境下线性调频脉冲、巴克码、频率步进脉冲雷达MTI、脉冲压缩【附MATLAB代码】
来源:微信公众号:EW Frontier 本代码主要模拟杂波环境(飞机、地杂波、鸟类信号)下,Chirp脉冲、巴克码脉冲、频率步进脉冲雷达信号的脉冲压缩及MTI、匹配滤波。 MATLAB主代码 % 定义参数 fs 1000; % 采样率 T 1; …...
)
前端最新面试题(Javascript模块篇)
目录 1 数据类型基础 1.1 JS内置类型 1.2 null和undefined区别 1.3 null是对象吗?为什么? 1.4 1.toString()为什么可以调用? 1.5 0.1+0.2为什么不等于0.3?如何让其相等 1.6 如何理解BigInt 1.7 JS 整数是怎么表示的 1.8 Number() 的存储空间是多大?如果后台发送了…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

