LeetCode 124 —— 二叉树中的最大路径和
阅读目录
- 1. 题目
- 2. 解题思路
- 3. 代码实现
1. 题目
2. 解题思路
二叉树的问题首先我们要想想是否能用递归来解决,本题也不例外,而递归的关键是找到子问题。
我们首先来看看一棵最简单的树,也就是示例 1。这样的一棵树总共有六条路径,分别是:根节点、左节点-根节点、右节点-根节点、左节点、右节点、左节点-根节点-右节点,我们用一个大小为 6 的数组 rootSum 来分别表示这六条路径的路径和,那么所求的最大路径和即为 rootSum 的最大值。
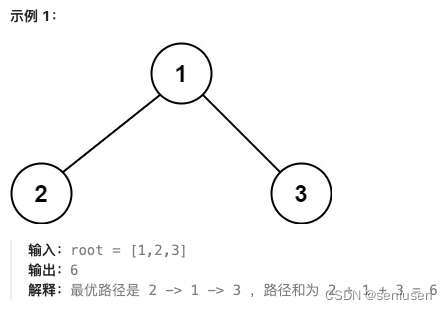
需要注意,当某一个节点为空的时候,比如左节点为空,那么左节点-根节点路径和为根节点的值,左节点贡献值为 0。而单独左节点的路径不存在,路径和应该设置为一个极大的负值。
接下来,我们再考虑一个更复杂的树,这棵树的根节点有左右两棵子树,每一棵子树都是类似上面示例 1 的一棵树。那么,我们可以很容易地得到左右子树的路径和数组 leftSum 和 rightSum ,接下来,我们要做的就是如何根据这两个数组得到整棵树的路径和数组 rootSum ?
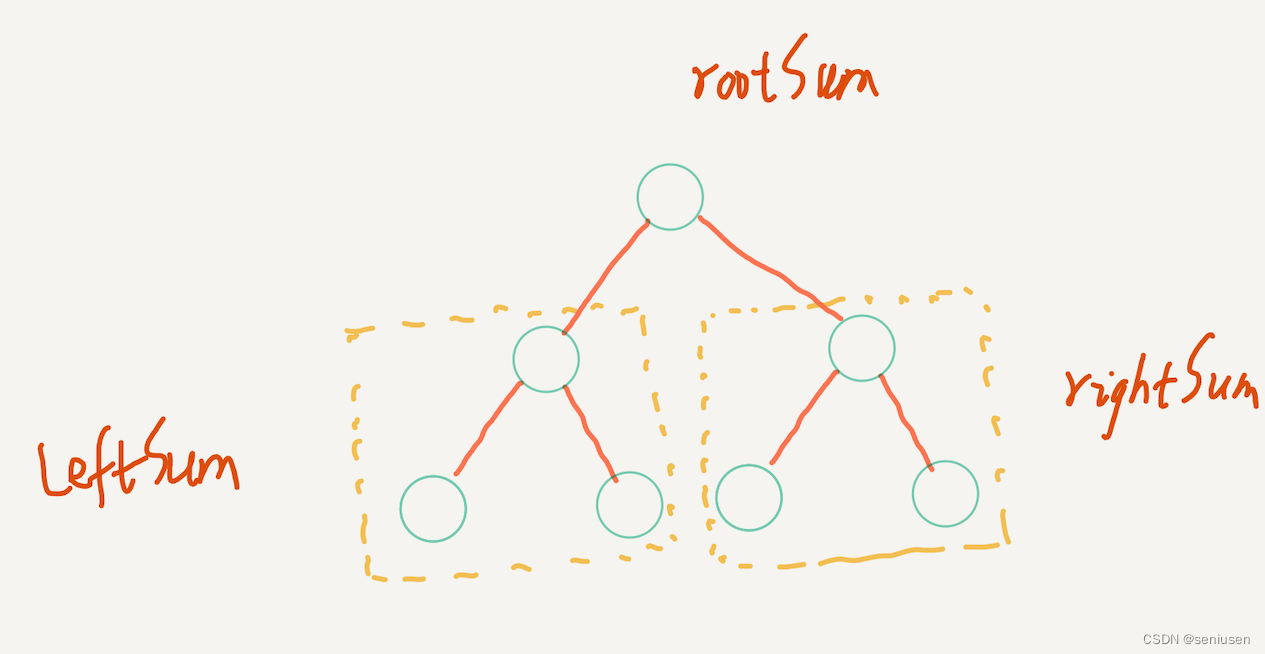
rootSum 仍然有 6 条路径,其中:
- 只有一个根节点的路径,
rootSum[0]=root->val - 左节点-根节点的路径,这时候由于左节点是一棵子树,所以,只有包含子树中根节点的路径才能继续和当前的根节点组成新的路径,也就是子树的前三条路径,然后我们取其中最大的一条即可,
rootSum[1]=root->val + max(leftSum[0:3)) - 右节点-根节点的路径,这个和上面的类似,
rootSum[2]=root->val + max(rightSum[0:3)) - 左节点,也即是单独左子树组成的最大路径,
rootSum[3]=max(leftSum[0:6)) - 右节点,也即是单独右子树组成的最大路径,
rootSum[4]=max(rightSum[0:6)) - 左节点-根节点-右节点,也就是左子树的路径包含左子树的根节点,右子树的路径包含右子树的根节点,
rootSum[5]=max(leftSum[0:3))+ root->val + max(rightSum[0:3))
时间复杂度为 O ( n ) O(n) O(n), n n n 代表节点总数,每个节点都需要进行遍历一次,空间复杂度为 O ( n ) O(n) O(n),每个节点都需要存储 6 个状态值。
3. 代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> getNodePathSum(TreeNode* root) {int leftRootSum = 0, leftMaxSum = -10000;if (root->left != nullptr) {vector<int> leftSum = getNodePathSum(root->left);leftRootSum = *std::max_element(leftSum.begin(), leftSum.begin() + 3);leftMaxSum = *std::max_element(leftSum.begin(), leftSum.end());}int rightRootSum = 0, rightMaxSum = -10000;if (root->right != nullptr) {vector<int> rightSum = getNodePathSum(root->right);rightRootSum = *std::max_element(rightSum.begin(), rightSum.begin() + 3);rightMaxSum = *std::max_element(rightSum.begin(), rightSum.end());}vector<int> rootSum(6, 0);rootSum[0] = root->val;rootSum[1] = leftRootSum + root->val;rootSum[2] = rightRootSum + root->val;rootSum[3] = leftMaxSum;rootSum[4] = rightMaxSum;rootSum[5] = leftRootSum + root->val + rightRootSum;return rootSum;}int maxPathSum(TreeNode* root) {vector<int> sum = getNodePathSum(root);return *std::max_element(sum.begin(), sum.end());}
};
相关文章:

LeetCode 124 —— 二叉树中的最大路径和
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 二叉树的问题首先我们要想想是否能用递归来解决,本题也不例外,而递归的关键是找到子问题。 我们首先来看看一棵最简单的树,也就是示例 1。这样的一棵树总共有六条路径…...

美甲店会员预约系统管理小程序的作用是什么
女性爱美体现在方方面面,美丽好看的指甲也不能少,市场中美甲店、小摊不少,也跑出了不少连锁品牌,70后到00后,每个层级都有不少潜在客户,商家需要获取和完善转化路径,不断提高品牌影响力与自身内…...

..堆..
堆 堆是完全二叉树,即除了最后一列之外,上面的每一层都是满的(左右严格对称且每个节点都满子节点) 最后一列从左向右排序。 默认大根堆:每一个节点都大于其左右儿子,根节点就是整个数据结构的最大值 pr…...
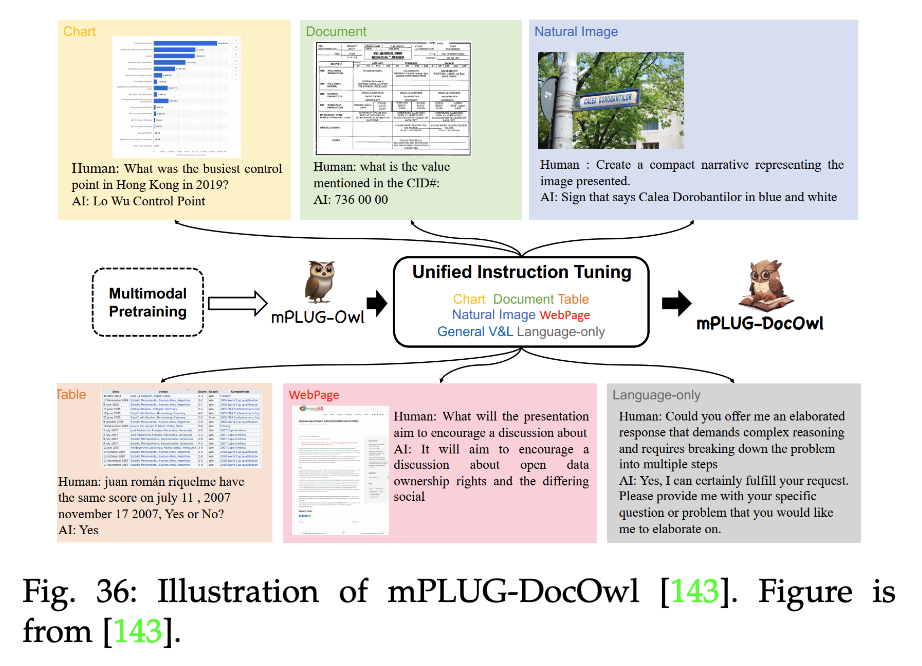
【LLM多模态】综述Visual Instruction Tuning towards General-Purpose Multimodal Model
note 文章目录 note论文1. 论文试图解决什么问题2. 这是否是一个新的问题3. 这篇文章要验证一个什么科学假设4. 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?5. 论文中提到的解决方案之关键是什么?6. 论文中的…...

探索Linux中的神奇工具:重定向符的妙用
探索Linux中的神奇工具:重定向符的妙用 在Linux系统中,重定向符是一个强大的工具,用于控制命令的输入和输出,实现数据流的定向。本文将详细介绍重定向符的基本用法和一些实用技巧,帮助读者更好地理解和运用这个功能。…...

Kubernetes 文档 / 概念 / 工作负载 / 工作负载管理 / Job
Kubernetes 文档 / 概念 / 工作负载 / 工作负载管理 / Job 此文档从 Kubernetes 官网摘录 中文地址 英文地址 Job 会创建一个或者多个 Pod,并将继续重试 Pod 的执行,直到指定数量的 Pod 成功终止。 随着 Pod 成功结束,Job 跟踪记录成功完成的…...
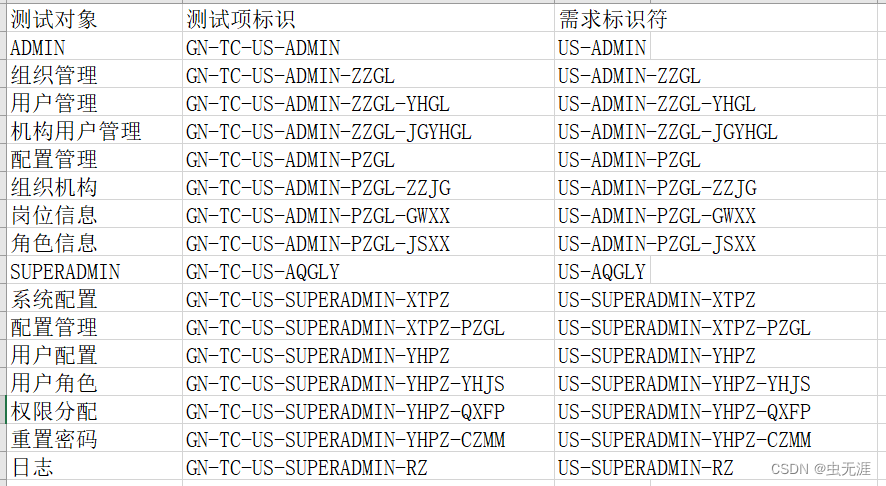
办公自动化-Python如何提取Word标题并保存到Excel中?
办公自动化-Python如何提取Word标题并保存到Excel中? 应用场景需求分析实现思路实现过程安装依赖库打开需求文件获取word中所有标题去除不需要的标题创建工作簿和工作表分割标题功能名称存入测试对象GN-TC需求标识符存入测试项标识存入需求标识符 完整源码实现效果学…...
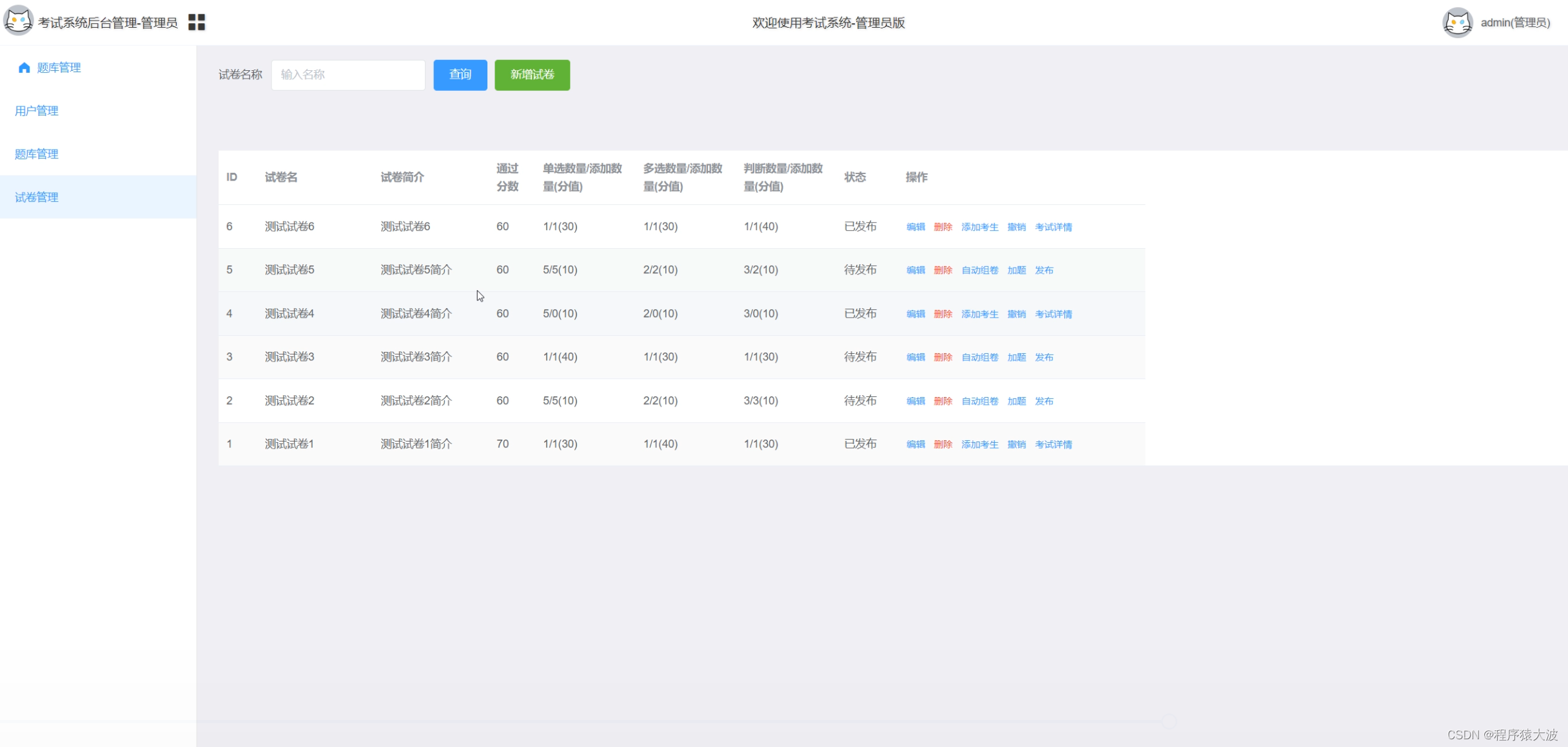
基于Java、SpringBoot和uniapp在线考试系统安卓APP和微信小程序
摘要 基于Java、SpringBoot和uniapp的在线考试系统安卓APP微信小程序是一种结合了现代Web开发技术和移动应用技术的解决方案,旨在为教育机构提供一个方便、高效和灵活的在线考试平台。该系统采用Java语言进行后端开发,使用SpringBoot框架简化企业级应用…...
)
抖音a-bogus加密解析(三)
要补的环境我给提示,大家自行操作,出了问题就是因为缺环境,没补好 window global; // reading _u未定义 window.requestAnimationFrame function () {} // XMLHttpRequest 未定义 window.XMLHttpRequest function () {} window.onwheelx …...

IS-IS DIS
原理概述 OSPF 协议支持4种网络类型, IS-IS 协议只支持两种网络类型,即广播网络和点到点网络。与 OSPF 协议相同, IS-IS 协议在广播网络中会将网络视为一个伪节点( Pseudonode ,简称 PSN ),并选举出一台 DIS ( Designa…...

random和range
含义: random(1,10) 不包含10,用于生成随机数。它可以生成浮点数或整数,取决于具体的使用方式。 range(0,1) 不包含1,用于生成一个整数序列。它可以生成一个指定范围内的连续整数序列。 区别在于&#x…...

研二学妹面试字节,竟倒在了ThreadLocal上,这是不要应届生还是不要女生啊?
一、写在开头 今天和一个之前研二的学妹聊天,聊及她上周面试字节的情况,着实感受到了Java后端现在找工作的压力啊,记得在18,19年的时候,研究生计算机专业的学生,背背八股文找个Java开发工作毫无问题&#x…...
实现)
Golang:gammazero/deque是一个快速环形缓冲区deque(双端队列)实现
gammazero/deque是一个快速环形缓冲区deque(双端队列)实现。 文档 https://github.com/gammazero/deque 安装 go get github.com/gammazero/deque代码示例 先入先出队列 package mainimport ("fmt""github.com/gammazero/deque&quo…...

C++ 时间处理-统计函数运行时间
1. 关键词2. 问题3. 解决思路4. 代码实现 4.1. timecount.h4.2. timecount.cpp 5. 测试代码6. 运行结果7. 源码地址 1. 关键词 C 时间处理 统计函数运行时间 跨平台 2. 问题 C如何简单便捷地实现“函数运行时间的统计”功能? 3. 解决思路 类的构造函数&#x…...
)
JAVA面试题大全(十五)
1、Zookeeper 是什么? zookper是一个分布式的,开放源码的分布式应用程序协调服务。是 google chubby 的开源实现,是 hadoop 和 hbase 的重要组件。它是一个为分布式应用提供一致性服务的软件,提供的功能包括:配置维护…...

使用python对指定文件夹下的pdf文件进行合并
使用python对指定文件夹下的pdf文件进行合并 介绍效果代码 介绍 对指定文件夹下的所有pdf文件进行合并成一个pdf文件。 效果 要合并的pdf文件,共计16个1页的pdf文件。 合并成功的pdf文件:一个16页的pdf文件。 代码 import os from PyPDF2 import …...

Day50 | 309.最佳买卖股票时机含冷冻期 714.买卖股票的最佳时机含手续费 总结
代码随想录算法训练营Day50 | 309.最佳买卖股票时机含冷冻期 714.买卖股票的最佳时机含手续费 总结 LeetCode 309.最佳买卖股票时机含冷冻期 题目链接:LeetCode 309.最佳买卖股票时机含冷冻期 思路: 四个状态。 保持持有股票,保持卖出股票…...

Steam在连接至服务器发生错误/连接服务器遇到问题解决办法
Steam作为全球最大的数字游戏分发平台,构建了一个活跃的玩家社区,用户可以创建个人资料,添加好友,组建群组,参与讨论,甚至直播自己的游戏过程。通过创意工坊,玩家还能分享自制的游戏模组、地图、…...

kafka 工作流程文件存储
爬虫组件分析 目录概述需求: 设计思路实现思路分析1.kafka 工作流程2.kafka 文件存储 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for…...

贪心算法4(c++)
过河的最短时间 题目描述 输入 在漆黑的夜里,N位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话,大家是无论如何也不敢过桥去的。不幸的是,N个人一共只带了一只手电筒,而桥窄得只够让两个人同时过,如果…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
