【NumPy】关于numpy.median()函数,看这一篇文章就够了
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式+人工智能领域,具备多年的嵌入式硬件产品研发管理经验。
📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向的学习指导、简历面试辅导、技术架构设计优化、开发外包等服务,有需要可加文末联系方式联系。
💬 博主粉丝群介绍:① 群内高中生、本科生、研究生、博士生遍布,可互相学习,交流困惑。② 热榜top10的常客也在群里,也有数不清的万粉大佬,可以交流写作技巧,上榜经验,涨粉秘籍。③ 群内也有职场精英,大厂大佬,可交流技术、面试、找工作的经验。④ 进群免费赠送写作秘籍一份,助你由写作小白晋升为创作大佬。⑤ 进群赠送CSDN评论防封脚本,送真活跃粉丝,助你提升文章热度。有兴趣的加文末联系方式,备注自己的CSDN昵称,拉你进群,互相学习共同进步。
关于numpy.median函数,看这一篇文章就够了
- 1. 引言:NumPy - Python数据科学的基石
- 2. numpy.median:中位数计算的艺术
- 2.1 numpy.median函数API详解
- 函数签名
- 返回值
- 2.2 示例代码与应用
- 基本使用:计算一维数组的中位数
- 沿特定轴计算二维数组的中位数
- 使用keepdims选项保持维度
- 3. numpy.median与其他统计函数的结合使用
- 综合应用示例
- 4. 总结

1. 引言:NumPy - Python数据科学的基石
NumPy,全称为Numerical Python,是Python语言的一个基础库,专为大规模数值计算而设计。它提供了一个高性能的多维数组对象ndarray,以及一套针对这些数组操作的工具。NumPy的出现极大地简化了数组操作,加速了数学、科学和工程计算中的数据处理过程,成为了数据科学、机器学习、图像处理等领域不可或缺的一部分。
2. numpy.median:中位数计算的艺术
在统计学中,中位数作为一组数据的中心趋势度量,指位于中间位置的数,即将数据从小到大排序后处于中间的数。对于奇数个数据点,中位数就是正中间的那个数;而对于偶数个数据点,则通常取中间两个数的平均值。numpy.median函数正是用来高效计算数组元素的中位数,支持沿指定轴计算,适应于多维数据处理。
2.1 numpy.median函数API详解
函数签名
numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)
- a:输入的NumPy数组。
- axis(可选):计算中位数的轴。默认为
None,表示计算整个数组的中位数。可以是整数或元组来指定多个轴。 - out(可选):如果提供,计算出的中位数会存储在这个数组中。该数组的形状和类型应该与预期的输出相同。
- overwrite_input(可选):布尔值,默认为
False。如果设置为True,则允许在计算过程中直接修改输入数组以节省内存。 - keepdims(可选):布尔值,默认为
False。如果为True,计算后的结果将保留输入数组的轴,并将其长度设为1。
返回值
- 计算得出的中位数,或者沿着指定轴的中位数数组。
2.2 示例代码与应用
基本使用:计算一维数组的中位数
import numpy as npdata = np.array([3, 1, 2, 5, 4])
median_value = np.median(data)
print("Median of the array:", median_value)
沿特定轴计算二维数组的中位数
matrix = np.array([[1, 3, 5], [2, 4, 6]])
# 计算每行的中位数
row_median = np.median(matrix, axis=1)
print("Median along rows:", row_median)# 计算每列的中位数
col_median = np.median(matrix, axis=0)
print("Median along columns:", col_median)
使用keepdims选项保持维度
# 计算每列中位数并保持维度
col_med_keepdims = np.median(matrix, axis=0, keepdims=True)
print("Column medians with keepdims:", col_med_keepdims)
3. numpy.median与其他统计函数的结合使用
在实际应用中,numpy.median常与numpy.mean(平均值)、numpy.percentile(百分位数)等统计函数联合使用,以全面分析数据分布。例如,结合平均值可以更全面地评估数据的集中趋势,而利用百分位数则能深入了解数据的分布范围和异常值情况。
综合应用示例
import numpy as np# 生成随机数据
random_data = np.random.randn(100)# 计算中位数、平均值和四分位数
median = np.median(random_data)
mean = np.mean(random_data)
quartiles = np.percentile(random_data, [25, 50, 75])print("Median:", median)
print("Mean:", mean)
print("Quartiles:", quartiles)
4. 总结
numpy.median作为一个强大的统计函数,不仅在单一维度上快速准确地提供了数据集的中位数,还支持多维度数据的分析,通过灵活的轴参数和keepdims选项,使得处理复杂数据结构变得轻而易举。结合NumPy库的其他功能,开发者和数据分析师能够深入挖掘数据特征,做出更为精准的分析和预测。在数据科学日益重要的今天,熟练掌握numpy.median及与其相关的统计方法,对于提升数据分析能力具有重要意义。无论是学术研究、金融分析、还是机器学习项目,numpy.median都是处理连续型数据、识别数据分布模式、及进行稳健统计分析不可或缺的工具。
相关文章:

【NumPy】关于numpy.median()函数,看这一篇文章就够了
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...

起保停电路工作原理
一、电路组成 起保停电路由电源保护设备(空气开关)、交流接触器、启动按钮、停止按钮和用电设备组成。 起保停电路的组成部分通常可分为四个部分: 保护部分:(空气开关)在电流或电压超出一定范围时自动切断…...

【Vue】Vue2使用ElementUI
目录 Element UI介绍特点Vue2使用Element安装引入ElementUI组件库 使用ElementUI用户注册列表展示其他 mint-ui介绍特点安装组件引入组件Mint-ui相关组件 Element UI 介绍 官网(基于 Vue 2.x ):https://element.eleme.cn/#/zh-CN ElementUI 是一个基于 Vue.js 的桌面端组件库…...

设计模式在芯片验证中的应用——模板方法
一、模板方法 模板方法(Template Method)设计模式是一种行为设计模式, 它在父类中定义了一个功能的框架, 允许子类在不修改结构的情况下重写功能的特定步骤。也就是模板方法定义了一组有序执行的操作,将一些步骤的实现留给子类,同…...

Webpack Bundle Analyzer:深入分析与优化你的包
Webpack Bundle Analyzer是一个用于可视化的工具,它可以帮助你分析Webpack打包后的输出文件,查看哪些模块占用了最多的空间,从而进行优化。 2500G计算机入门到高级架构师开发资料超级大礼包免费送! 首先,你需要安装W…...

Java后端开发学习历程
1、JavaWeb------------------------>19天 2、SSMSpringBoot------------->12天 3、瑞吉外卖项目------------------>15天 4、JavaSE-------------------------->25天 总耗时71天(2024.03.11——2024.05.26两个半月),Java后端…...

CentOS 7 socat命令端口转发
场景 开发排查问题需配置远程调试,但配置调试的服务器不支持外网访问,于是就考虑到用端口转发的方式让开发进行远程调试,转发工具比如有:rinetd等等,意外看到使用socat做转发更简单方便,下面就记录一下 命令简介 socat 是一个功能强大的网络工具,可以在两个连接的数据…...

vue全局修改设置滚动条样式
vue全局修改设置滚动条样式 具体代码: ::-webkit-scrollbar{ /*滚动条整体样式*/width: 6px; /*高宽分别对应横竖滚动条的尺寸*/height: 1px; } ::-webkit-scrollbar-thumb{ /*滚动条里面小方块*/border-radius: 5px;background: #cfcbcb; } ::-webkit-scrollbar-…...
✨聚梦AI绘图插件-for photoshop(基于ComfyUI) 内测版V0.1发布
🎈背景 photoshop本身是有AI生成能力的,不过限于种种原因,国内使用很不方便。 photoshop也是有AI插件的,不过大多安装起来比较复杂,或者,干脆就会收费。 所以我们做了一个免费的AI插件,期望能…...
java “错误:编码GBK 的不可映射字符”
环境:JDK-17 本机编码:utf-8 代码编码:GBK 错误:java “错误:编码GBK 的不可映射字符” 解决1:记事本打开java源文件,另存为选择ANSI编码 解决2:复制代码再将编码格式改为utf-8,…...
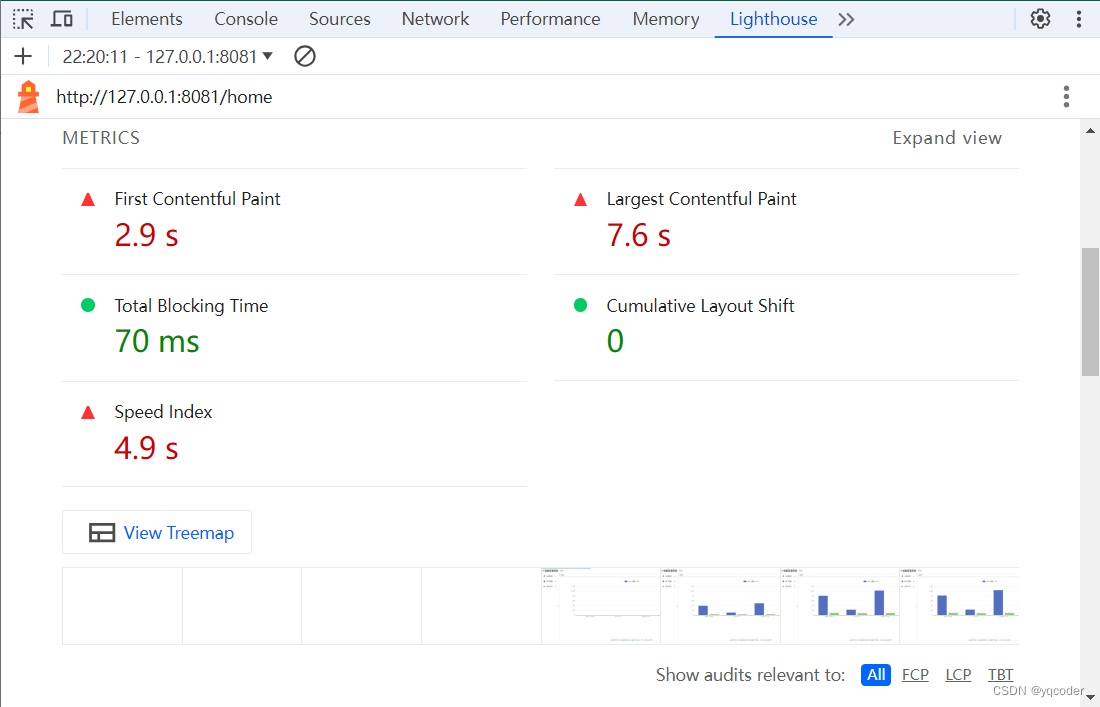
前端 JS 经典:Web 性能指标
什么是性能指标:Web Performance Metrics 翻译成 Web 性能指标,一般和时间有关系,在短时间内做更多有意义的事情。 一个站点表现得好与不好,标准在于用户体验,而用户体验好不好,有一套 RAIL 模型来衡量。这…...
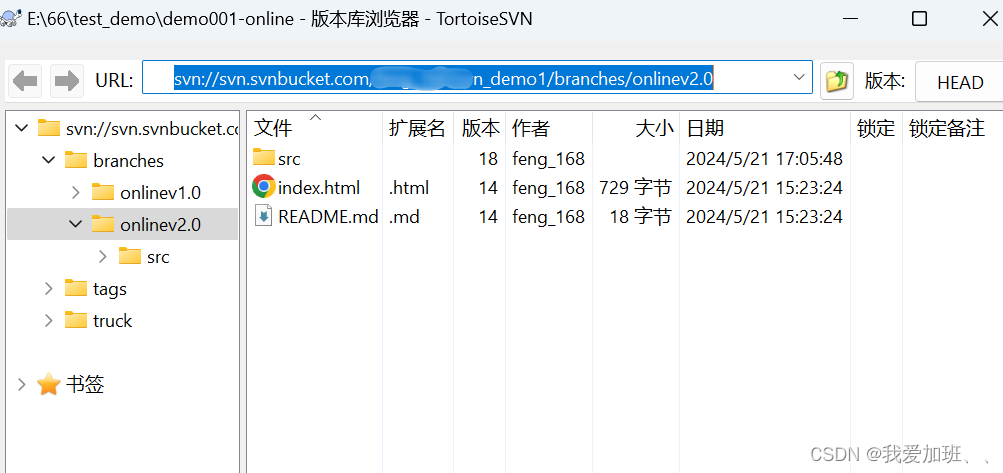
SVN创建分支,分支合并,切换分支。通俗易懂
1、首先在svnbucket.com远程仓库上创建项目,这里我创建了个测试demo: 2、先把svn仓库的项目检出到自己的文件夹,我这里是demo001文件夹,此时并没有创建truck, branches, tags这三个目录: 3、 在demo001文件夹里新建tru…...

【编译原理复习笔记】中间语言
中间语言 中间语言的特点和作用 (1)独立于机器 (2)复杂性介于源语言和目标语言之间 中间语言可以使编译程序的结构在逻辑上更为简单明确 常用的中间语言 后缀式 图表示:抽象语法树,有向无环图 三地址代…...

linux笔记6--shell相关
文章目录 1. 查看当前的shell类型2. ps -f命令3. 父子shell4. 分号在命令里的作用问题:环境变量echo: 5. sleep和jobssleep:jobs:例子:&: 6. 外部命令和内建命令图解外部命令type命令 7. history命令8. alias命令9. 推荐 1. 查看当前的sh…...

链表-线性表的链式表示
链表-线性表的链式表示 #mermaid-svg-ozpXrKnNCyYdqHvN {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-ozpXrKnNCyYdqHvN .error-icon{fill:#552222;}#mermaid-svg-ozpXrKnNCyYdqHvN .error-text{fill:#552222;stro…...

GNU/Linux - 时区设置
CST China Standard Time 北京时间/中国标准时间 在时区划分上,属东八区,比协调世界时早 8 小时,记为 UTC8 GMT Greenwich Mean Time 格林威治标准时间 是指位于英国伦敦郊区的格林尼治天文台的标准时间,因为本初子午线被定…...

红队攻防渗透技术实战流程:云安全之云原生安全:内核漏洞和版本漏洞
红队云攻防实战 1. 云原生安全 -Docker安全-容器逃逸-版本漏洞1.1 容器逃逸-版本漏洞-runC容器逃逸1.2 实战案例-版本漏洞-runC容器逃逸1.3 容器逃逸-版本漏洞-containerd逃逸1.4 实战案例-版本漏洞-containerd逃逸1.5 Docker安全-容器逃逸-CDK自动化1.6 Docker安全-容器逃逸-c…...

spring状态机实战
一、什么是状态机 状态机是有限状态自动机的简称,是现实事物运行规则抽象而成的一个数学模型,是一种概念性机器,它能采取某种操作来响应一个外部事件。这种操作不仅能取决于接收到的事件,还能取决于各个事件的相对发生顺序。状态…...

Ubuntu系统上安装NVIDIA驱动【笔记】
Ubuntu上安装NVIDIA驱动,您可以按照以下步骤操作: 首先,您需要配置软件源(根据情况配置,否则影响更新和下载速度)。 接下来,您可以按照上一条回答中的步骤来安装新的NVIDIA驱动。首先ÿ…...
生成式AI导论2024-李宏毅
生成式AI导论2024-李宏毅 第0讲: 课程说明第1讲:生成式AI是什么第2講:今日的生成式人工智慧厲害在哪裡?從「工具」變為「工具人」 第0讲: 课程说明 生成式AI的入门课程 第1讲:生成式AI是什么 生成式人…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

CppCon 2015 学习:Simple, Extensible Pattern Matching in C++14
什么是 Pattern Matching(模式匹配) ❝ 模式匹配就是一种“描述式”的写法,不需要你手动判断、提取数据,而是直接描述你希望的数据结构是什么样子,系统自动判断并提取。❞ 你给的定义拆解: ✴ Instead of …...
