Leetcode 剑指 Offer II 079.子集
题目难度: 中等
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
给定一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
- 输入:nums = [1,2,3]
- 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
- 输入:nums = [0]
- 输出:[[],[0]]
提示:
- 1 <= nums.length <= 10
- -10 <= nums[i] <= 10
- nums 中的所有元素 互不相同
题目思考
- 如果限制只能用递归或者迭代, 如何解决?
解决方案
方案 1
思路
- 首先我们可以尝试用递归的思路来解决
- 观察幂集的特点, 我们可以发现它的每个子集都可以细分成两种情况: 使用原集合的某个元素以及不使用该元素
- 大家可以将整个过程想象成一个二叉树: 每遍历到原集合的一个元素, 都可以将其分成两个分支继续向下, 直到遍历完所有元素为止
- 我们可以基于上述分析进行递归求解, 具体做法如下:
- 传入当前下标以及当前使用的元素组成的列表
- 然后递归调用下一下标, 此时分为两种情况: 使用当前元素和不使用当前元素
- 最后递归出口是下标达到原集合长度, 此时形成的列表即为幂集的其中一个子集
- 由于原集合中不包含重复元素, 所以每个递归出口形成的列表也各不相同, 无需手动去重
复杂度
- 时间复杂度 O(2^N): 每遍历一个元素我们都有两种选择, 所以总时间是 2^N
- 空间复杂度 O(N): 递归栈的消耗, 对应的是上述分析中二叉树的高度, 即原集合长度 N
代码
Python 3
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:# 方法1: 递归传入当前下标和列表res = []def getSet(i, cur):if i == len(nums):# 递归出口, 将其加入最终结果集res.append(cur)return# 两种情况/分支getSet(i + 1, cur)getSet(i + 1, cur + [nums[i]])getSet(0, [])return res
方案 2
思路
- 接下来我们尝试用迭代的思路来解决
- 根据方案 1 的分析, 我们不难发现幂集的所有子集都可以用一个长度为 N 的 mask 来表示 (N 是原集合长度)
- 其中 mask 的第 i 位为 1 就对应使用下标 i 的元素, 为 0 则不使用
- 所以我们可以依次遍历[0, 2^N-1], 统计其哪些位为 1, 从而得到对应的子集并加入结果集即可
复杂度
- 时间复杂度 O(N*2^N): 需要遍历 2^N 个元素, 内层循环需要遍历 N 位得到具体的子集
- 空间复杂度 O(1): 只使用了几个常数空间的变量 (结果集占用的空间不计算在内)
代码
Python 3
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:# 方法2: 迭代+位运算n = len(nums)res = []for mask in range(1 << n):cur = []for i in range(n):if (mask >> i) & 1:# 第 i 位为 1, 使用对应下标 i 的元素cur.append(nums[i])res.append(cur)return res
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊

相关文章:

Leetcode 剑指 Offer II 079.子集
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定一个整数数组 nums ,数组中的元素 互不相同 。返…...

Linux基础命令常见问题解决方案
Linux 基础命令常见问题解决方案 在Linux的日常使用中,用户经常会遇到各种各样的问题。本文旨在提供一个关于Linux基础命令的常见问题及其解决方案的全面指南。我们将覆盖30种不同的错误场景,并给出具体的解决步骤和示例,帮助初学者快速定位…...
 ——使用LINQ进行匿名对象初始化)
LINQ(五) ——使用LINQ进行匿名对象初始化
总目录 C# 语法总目录 上一篇:LINQ(四) ——使用LINQ进行对象类型初始化 LINQ 五 ——使用LINQ进行匿名对象初始化 6.2 匿名类型 6.2 匿名类型 可以不用声明定义一个对象,直接使用new,然后直接赋值即可 string[] names { "Tom",…...
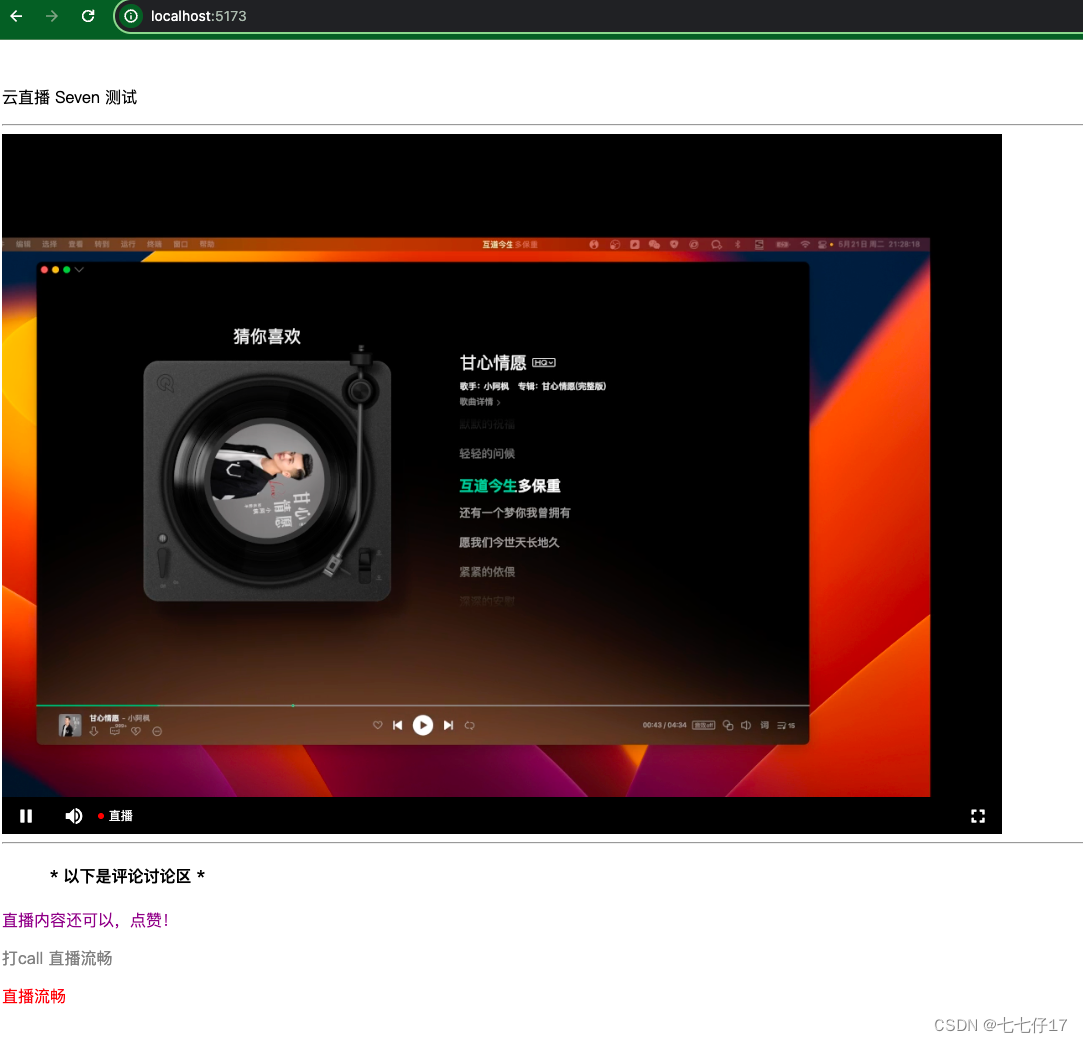
1小时从0开始搭建自己的直播平台(详细步骤)
本文讲述了如何从0开始,利用腾讯云的平台,快速搭建一个直播平台的过程。 文章目录 效果图详细步骤准备工作第一步:添加域名并检验cname配置1.先填加一个推流域名2. 点击完下一步,得到一个cname地址3. 将cname地址,配置…...

Python打包篇-exe
文章目录 pyinstallerauto-py-to-exe pyinstaller 命令行工具,语法自行查看官方help pip install pyinstallerauto-py-to-exe 基于pyinstaller的一款GUI工具,会自行打包py文件中依赖的库 pip install auto-py-to-exe auto-py-to-exe.exe //运行即可...

游戏找不到d3dcompiler_43.dll怎么办,教你5种可靠的修复方法
在电脑使用过程中,我们经常会遇到一些错误提示,其中之一就是“找不到d3dcompiler43.dll”。这个问题通常出现在游戏或者图形处理软件中,它会导致程序无法正常运行。为了解决这个问题,我经过多次尝试和总结,找到了以下五…...

如何使用多种算法解决LeetCode第135题——分发糖果问题
❤️❤️❤️ 欢迎来到我的博客。希望您能在这里找到既有价值又有趣的内容,和我一起探索、学习和成长。欢迎评论区畅所欲言、享受知识的乐趣! 推荐:数据分析螺丝钉的首页 格物致知 终身学习 期待您的关注 导航: LeetCode解锁100…...
泰拉瑞亚从零开始的开服教程
前言 本教程将讲诉使用Linux系统搭建泰拉瑞亚服务器(因为网上已经有很完善的windows开服教程了),使用的Linux发行版是Debian11,服务端使用的程序是TShock,游戏版本是1.4.4.9 所需要准备的 一台服务器(本教程使用的是…...
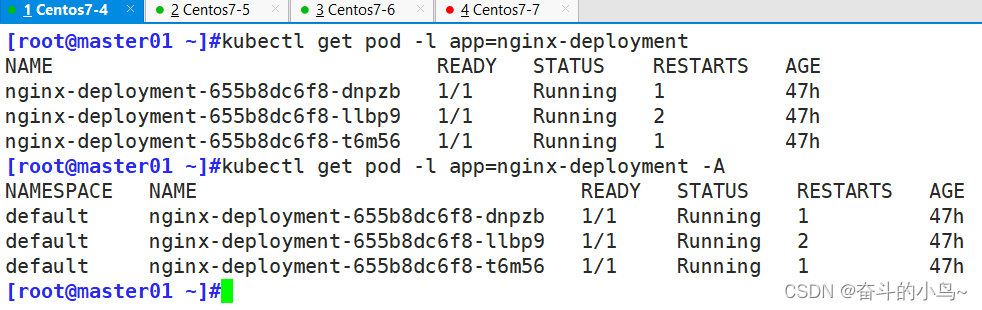
【云原生】K8s管理工具--Kubectl详解(一)
一、陈述式管理 1.1、陈述式资源管理方法 kubernetes 集群管理集群资源的唯一入口是通过相应的方法调用 apiserver 的接口kubectl 是官方的 CLI 命令行工具,用于与 apiserver 进行通信,将用户在命令行输入的命令,组织并转化为apiserver 能识…...

2024.5.26.python.exercise
# # 导入包 # from pyecharts.charts import Bar, Timeline # from pyecharts.options import LabelOpts, TitleOpts # from pyecharts.globals import ThemeType # # # 从文件中读取信息 # GDP_file open("1960-2019全球GDP数据.csv", "r", encoding&quo…...
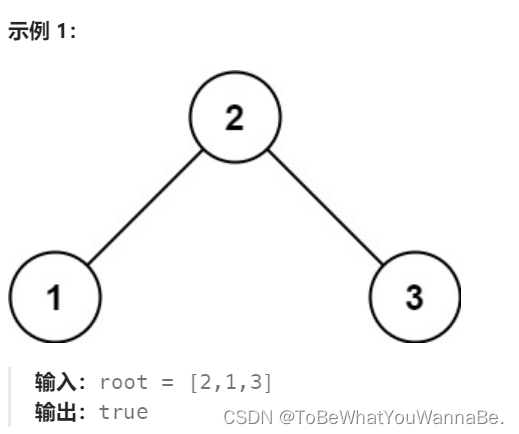
代码随想录-Day20
654. 最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums…...

揭秘C++ String容器:字符串操作的艺术
目录 编辑 引言 一、初识std::string:构造与初始化 二、字符串的操纵艺术:拼接、查找与替换 三、访问与遍历:字符的细腻触感 四、大小与容量:动态调整的智慧 五、进阶功能:探索更多可能 结语 引言 在C标准库…...

【C++】牛客 ——DP36 abb
✨题目链接: DP36 abb ✨题目描述 leafee 最近爱上了 abb 型语句,比如“叠词词”、“恶心心” leafee 拿到了一个只含有小写字母的字符串,她想知道有多少个 "abb" 型的子序列? 定义: abb 型字符串满足以下…...

SpringBoot如何实现跨域?
定义一个配置类,实现WebMvcConfigurer接口,重写addCorsMappings方法 Configuration public class CorsConfig implements WebMvcConfigurer {Overridepublic void addCorsMappings(CorsRegistry registry) {registry.addMapping("/**").allow…...

SW 草图偏移 先预选
因为有些不能用链全部选,可以先框选要偏移的,再点偏移命令...

5.23 Linux中超时检测方式+模拟面试
1.IO多路复用的原理? IO多路复用使得一个或少量线程资源处理多个连接的IO事件的技术。对于要处理的多个阻塞的IO操作,建立集合并存储它们的文件描述符,利用单个阻塞函数去监控集合中文件描述符事件到达的情况,(如果到…...

MySQL数据表索引命名规范
在数据库设计和开发过程中,索引是提高查询性能的重要工具。合理的索引命名规范不仅能提高代码的可读性,还能便于维护和管理。本文将详细介绍MySQL数据表索引的命名规范,包括不同类型索引的命名方法,并提供多个代码示例以说明如何命…...

python内置函数map/filter/reduce详解
在Python中,map(), filter(), 和 reduce() 是内置的高级函数(实际是class),用于处理可迭代对象(如列表、元组等)的元素。这些函数通常与lambda函数一起使用,以简洁地表达常见的操作。下面我将分别解释这三个函数。 1. …...

PICO VR眼镜定制播放器使用说明文档videoplayerlib-ToB.apk
安装高级定制播放器 高级定制播放器下载地址:https://download.csdn.net/download/ahphong/89360454 仅限用于PICO G2、G3、G4、NEO系列VR眼镜上使用, 用途:用于第三方APP(开发者)调用定制播放器播放2D、3D、180、360全景视频。 VR眼镜系统请升级到最新版,可在官网下载,…...
基于51单片机的超声波液位测量与控制系统
基于51单片机液位控制器 (仿真+程序+原理图PCB+设计报告) 功能介绍 具体功能: 1.使用HC-SR04测量液位,LCD1602显示; 2.当水位高于设定上限的时候,对应声光报警报警&am…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
