用c++用4个凸函数(觉得啥好用用啥)去测试adam,rmsprop,adagrad算法的性能(谁先找到最优点)
为了测试 Adam、RMSProp 和 Adagrad 算法的性能,你可以使用四个凸函数进行实验。以下是一些常用的凸函数示例:
Rosenbrock 函数:
Booth 函数:
Himmelblau 函数:
Beale 函数:
你可以选择其中一个或多个函数来测试算法的性能。对于每个函数,你可以使用不同的初始点,并应用 Adam、RMSProp 和 Adagrad 算法来寻找最优点。最优点可以通过达到较低的函数值或满足预定精度条件来定义。
在实验过程中,你可以记录每个算法在不同函数和初始点上找到最优点的迭代次数、计算时间以及最终的函数值。通过比较这些指标,你可以评估每个算法的性能和效果。
请注意,算法的性能可能会因函数的形状和参数设置而有所不同。因此,建议你在不同的凸函数上进行多次实验,以获得更全面的性能比较结果。
#include <iostream>
#include <cmath>
#include <vector>// 定义凸函数类
class ConvexFunction {
public:virtual double evaluate(const std::vector<double>& x) = 0;
};// Rosenbrock 函数
class RosenbrockFunction : public ConvexFunction {
public:double evaluate(const std::vector<double>& x) override {double sum = 0.0;for (size_t i = 0; i < x.size() - 1; ++i) {double term1 = pow(x[i + 1] - pow(x[i], 2), 2);double term2 = pow(1 - x[i], 2);sum += 100 * term1 + term2;}return sum;}
};// Booth 函数
class BoothFunction : public ConvexFunction {
public:double evaluate(const std::vector<double>& x) override {double term1 = pow(x[0] + 2 * x[1] - 7, 2);double term2 = pow(2 * x[0] + x[1] - 5, 2);return term1 + term2;}
};// Himmelblau 函数
class HimmelblauFunction : public ConvexFunction {
public:double evaluate(const std::vector<double>& x) override {double term1 = pow(pow(x[0], 2) + x[1] - 11, 2);double term2 = pow(x[0] + pow(x[1], 2) - 7, 2);return term1 + term2;}
};// Beale 函数
class BealeFunction : public ConvexFunction {
public:double evaluate(const std::vector<double>& x) override {double term1 = pow(1.5 - x[0] + x[0] * x[1], 2);double term2 = pow(2.25 - x[0] + x[0] * pow(x[1], 2), 2);double term3 = pow(2.625 - x[0] + x[0] * pow(x[1], 3), 2);return term1 + term2 + term3;}
};// Adam 算法
std::vector<double> adam(const ConvexFunction& func, const std::vector<double>& initial_x, double learning_rate, int max_iterations) {std::vector<double> x = initial_x;std::vector<double> m(x.size(), 0.0);std::vector<double> v(x.size(), 0.0);double beta1 = 0.9;double beta2 = 0.999;double epsilon = 1e-8;for (int i = 0; i < max_iterations; ++i) {// 计算梯度std::vector<double> gradient(x.size(), 0.0);for (size_t j = 0; j < x.size(); ++j) {std::vector<double> x_plus_delta = x;x_plus_delta[j] += epsilon;double f_plus_delta = func.evaluate(x_plus_delta);gradient[j] = (f_plus_delta - func.evaluate(x)) / epsilon;}// 更新参数for (size_t j = 0; j < x.size(); ++j) {m[j] = beta1 * m[j] + (1 - beta1) * gradient[j];v[j] = beta2 * v[j] + (1 - beta2) * pow(gradient[j], 2);double m_hat = m[j] / (1 - pow(beta1, i + 1));double v_hat = v[j] / (1 - pow(beta2, i + 1));x[j] -= learning_rate * m_hat / (sqrt(v_hat) + epsilon);}}return x;
}// RMSProp 算法
std::vector<double> rmsprop(const ConvexFunction& func, const std::vector<double>& initial_x, double learning_rate, double decay_rate, int max_iterations) {std::vector<double> x = initial_x;std::vector<double> cache(x.size(), 0.0);double epsilon = 1e-8;for (int i = 0; i < max_iterations; ++i) {// 计算梯度std::vector<double> gradient(x.size(), 0.0);for (size_t j = 0; j < x.size(); ++j) {std::vector<double> x_plus_delta = x;x_plus_delta[j] += epsilon;double f_plus_delta = func.evaluate(x_plus_delta);gradient[j] = (f_plus_delta - func.evaluate(x)) / epsilon;}// 更新参数for (size_t j = 0; j < x.size(); ++j) {cache[j] = decay_rate * cache[j] + (1 - decay_rate) * pow(gradient[j], 2);x[j] -= learning_rate * gradient[j] / (sqrt(cache[j]) + epsilon);}}return x;
}// Adagrad 算法
std::vector<double> adagrad(const ConvexFunction& func, const std::vector<double>& initial_x, double learning_rate, int max_iterations) {std::vector<double> x = initial_x;std::vector<double> cache(x.size(), 0.0);double epsilon = 1e-8;for (int i = 0; i < max_iterations; ++i) {// 计算梯度std::vector<double> gradient(x.size(), 0.0);for (size_t j = 0; j < x.size(); ++j) {std::vector<double> x_plus_delta = x;x_plus_delta[j] += epsilon;double f_plus_delta = func.evaluate(x_plus_delta);gradient[j] = (f_plus_delta - func.evaluate(x)) / epsilon;}// 更新参数for (size_t j = 0; j < x.size(); ++j) {cache[j] += pow(gradient[j], 2);x[j] -= learning_rate * gradient[j] / (sqrt(cache[j]) + epsilon);}}return x;
}int main() {// 创建凸函数对象RosenbrockFunction rosenbrock;BoothFunction booth;HimmelblauFunction himmelblau;BealeFunction beale;// 设置算法参数double learning_rate = 0.01;double decay_rate = 0.9;int max_iterations = 1000;// 初始化初始点std::vector<double> initial_x = { 0.0, 0.0 };// 使用 Adam 算法找到最优点std::vector<double> adam_result = adam(rosenbrock, initial_x, learning_rate, max_iterations);std::cout << "Adam Result: (" << adam_result[0] << ", " << adam_result[1] << ")" << std::endl;// 使用 RMSProp 算法找到最优点std::vector<double> rmsprop_result = rmsprop(rosenbrock, initial_x, learning_rate, decay_rate, max_iterations);std::cout << "RMSProp Result: (" << rmsprop_result[0] << ", " << rmsprop_result[1] << ")" << std::endl;// 使用 Adagrad 算法找到最优点std::vector<double> adagrad_result = adagrad(rosenbrock, initial_x, learning_rate, max_iterations);std::cout << "Adagrad Result: (" << adagrad_result[0] << ", " << adagrad_result[1] << ")" << std::endl;return 0;
}
相关文章:

用c++用4个凸函数(觉得啥好用用啥)去测试adam,rmsprop,adagrad算法的性能(谁先找到最优点)
为了测试 Adam、RMSProp 和 Adagrad 算法的性能,你可以使用四个凸函数进行实验。以下是一些常用的凸函数示例: Rosenbrock 函数: Booth 函数: Himmelblau 函数: Beale 函数: 你可以选择其中一个或多…...
AJAX初级
AJAX的概念: 使用浏览器的 XMLHttpRequest 对象 与服务器通信 浏览器网页中,使用 AJAX技术(XHR对象)发起获取省份列表数据的请求,服务器代码响应准备好的省份列表数据给前端,前端拿到数据数组以后…...

重载大于号运算符,比较复数大小
本题目要求编写代码的功能为: 输入两个复数(变量名自拟),比较复数模的大小,复数实部与虚部都是整数 要求输入时输入4个整数,分别代表复数1的实部、虚部,复数2的实部虚部 输入格式: 在同一行中输…...
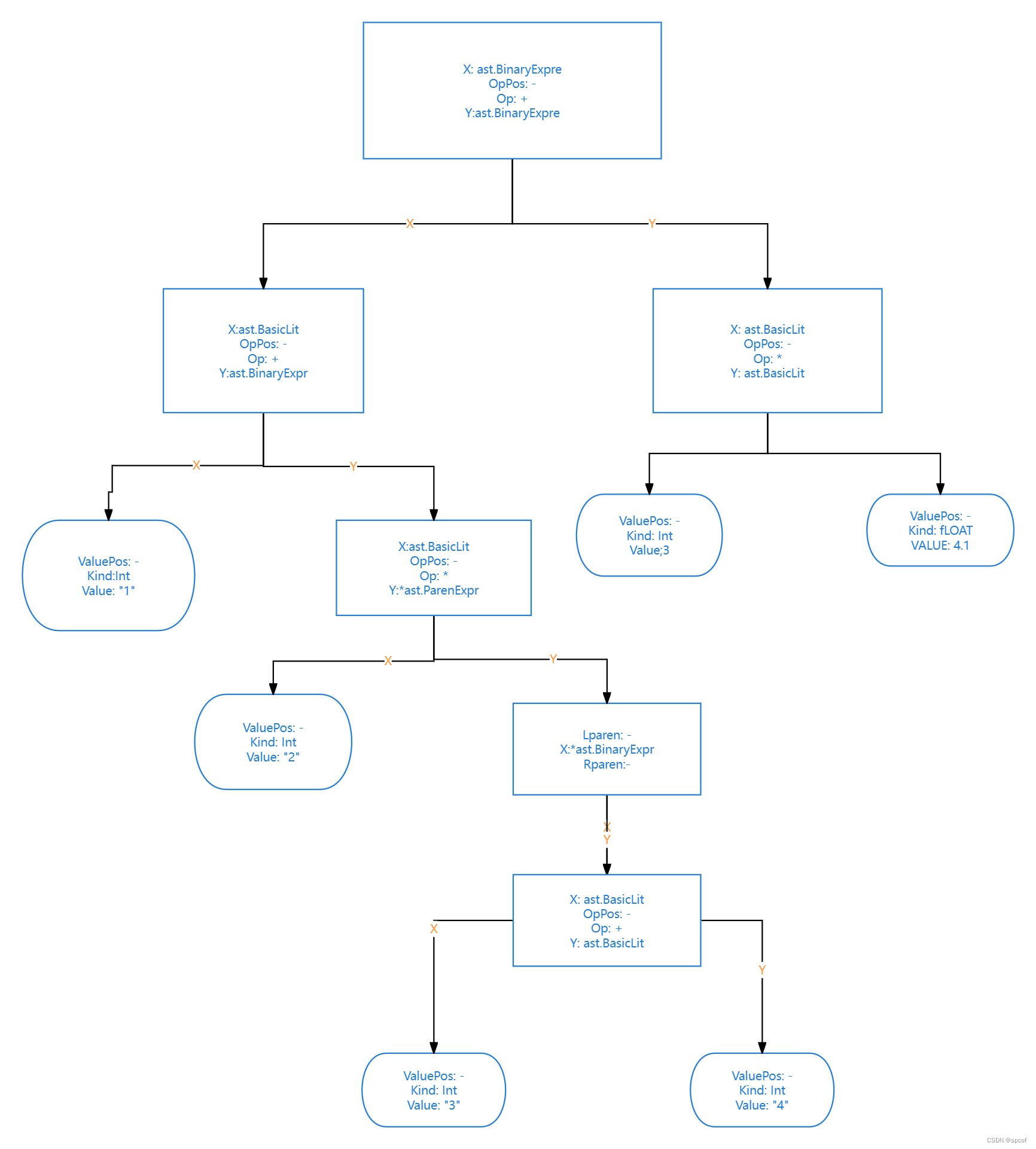
go ast语义分析实现指标计算器
什么是AST 首先我们要知道AST是什么(Abstract Syntax Tree,AST),简称为语法树,是go语言源代码语法结构的一种抽象表示。它以树状的形式表现编程语言的语法结构,树上的每个节点都表示源代码中的一种结构。 …...

【Vue】组件间传参与方法调用
【前言】 … 【目标】 1 了解组件间传参 2 组件间自定义事件绑定与解绑 3 组件的事件总线 4 消息订阅与发布 一 组件间传参 1 props 引入并使用组件:传递参数 <template><div id="app"><HelloWorld :msg="msg" :name="name" …...

类和对象2
三、C对象模型和this指针 3.1 成员变量和成员函数分开存储 在C中,类内的成员变量和成员函数分开存储,只有非静态成员变量才属于类的对象上 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> #include <string.h> using namespace …...
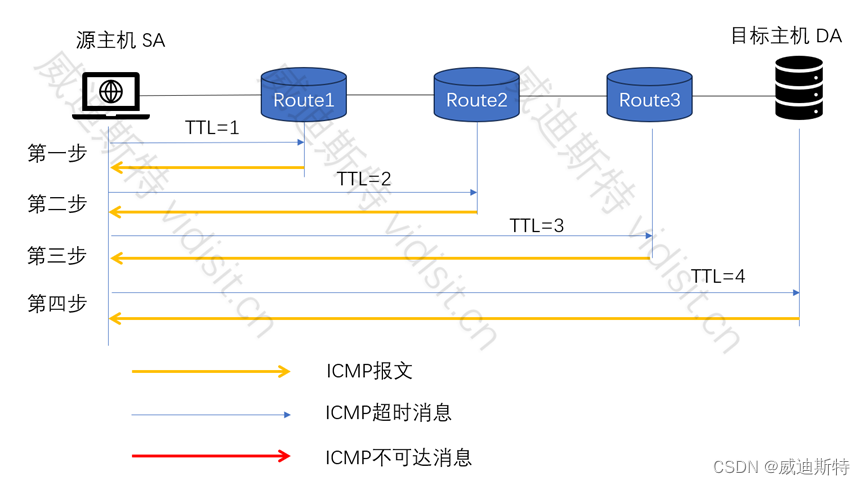
Linux系统命令traceroute详解(语法、选项、原理和实例)
目录 一、traceroute概述 二、语法 1、基本语法 2、命令选项 三、帮助信息 四、示例 1. 使用默认模式(ICMP Echo)追踪到目标主机 2. 使用UDP模式(需要root权限)追踪到目标主机 3. 不解析IP地址为主机名,直接显…...

中兴通讯助力中国移动,推动SPN AI节能技术于23省规模部署
SPN作为中国移动自主创新的新一代综合承载网络,相比PTN设备,SPN的单机容量及性能有大幅提升,整机功耗也相应变大。在当前国家双碳政策的目标下,SPN设备的节能降耗也日益成为中国移动关注的焦点。因此,中国移动选择与中…...

SQL Server--死锁
今天,客户反应打不开xxx页面了。好家伙肯定锁表了。。。。。 只能先吧死锁进程先kill掉,不能耽误客户生产环境运行。。。。。 一定要看看是那张表发生了死锁 1、查询死锁语句 select dbid,* from sys.sysprocesses where 11 and spid >50 and blo…...

中科蓝讯AB32VG1中文寄存器说明GPIO端口操作
1 GPIO管理 1.1 GPIO通用控制寄存器 寄存器 1- 1 GPIOA:端口 A 数据寄存器 位寄存器名模式缺省描述31:8---未使用7:0GPIOA写0x00PAx 数据。当 PAx 用作 GPIO 时有效 0:读取时PAx为输入低电平状态,写入时PAx为输出低电平; 1:PAx…...
如何查看热门GPT应用?
1、登陆chatgpt 2、访问 https://chatgpt.com/gpts 3、在该界面,可以搜索并使用image generator, Write For Me,Language Teature等热门应用。...

C++中的各种定义
文章目录 前言一、1、unsigned2、_countof、sizeof 总结 前言 一、 1、unsigned 在C语言中,"unsigned"是一个数据类型修饰符,用于修饰整数类型,表示该类型的变量只能存储非负整数,即无符号整数。它可以应用于char、s…...
)
Java面向对象-常用类(日期时间类)
常用类-日期时间类 Date(java.util.Date) – 日期类 SimpleDateFormat – 格式化日期类 Calendar – 日历类 1 Date类 java.util.Date类表示特定的瞬间,精确到毫秒。 package com.qf.datetime;import java.util.Date;public class Test01 {…...

Shell环境变量深入:自定义系统环境变量
Shell环境变量深入:自定义系统环境变量 目标 能够自定义系统级环境变量 全局配置文件/etc/profile应用场景 当前用户进入Shell环境初始化的时候会加载全局配置文件/etc/profile里面的环境变量, 供给所有Shell程序使用 以后只要是所有Shell程序或命令使用的变量…...
【C++课程学习】:命名空间的理解(图文详解)
🎁个人主页:我们的五年 🔍系列专栏:C课程学习 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 📷1.命名冲突 📷2.重定义 📷3.命名空间 🍺命名空间可…...

鸿蒙ArkUI-X平台差异化:【运行态差异化(@ohos.deviceInfo)】
平台差异化 简介 跨平台使用场景是一套ArkTS代码运行在多个终端设备上,如Android、iOS、OpenHarmony(含基于OpenHarmony发行的商业版,如HarmonyOS Next)。当不同平台业务逻辑不同,或使用了不支持跨平台的API…...

蓝牙Mesh模块组网时无线回程影响速率吗?
随着科技的发展,智能家居、智能办公等场景越来越广泛地应用于我们的生活。其中,蓝牙Mesh组网技术作为一种新型的无线通信技术,受到了越来越多用户的关注。那么,蓝牙Mesh模块在组网时无线回程过程中是否会影响速率呢?本…...

将3D检测的box框投影到BEV图片上
前言 点云数据作为一种丰富的三维空间信息表达方式,通常用于自动驾驶、机器人导航和三维建模等领域。然而,点云数据的直观性不如二维图像,这限制了它在一些需要快速视觉反馈的应用场景中的使用。本文将探讨如何将点云数据转换为二维图像&…...

Flutter 中的 ClipOval 小部件:全面指南
Flutter 中的 ClipOval 小部件:全面指南 在Flutter的丰富布局库中,ClipOval是一个用于裁剪子组件的显示区域为椭圆形或圆形的小部件。这种裁剪效果可以用于创建头像、图标或其他图形元素的美观边框。本文将提供ClipOval的全面指南,帮助你了解…...

ubuntu 硬盘转移
我插了两个 文件系统: ubuntu 硬盘转移: sudo dd if/dev/sdX1 of/dev/sdY1 bs128K convnoerror,sync statusprogressdd 的意思是DiskToDisk,if 是输入文件系统,of是输出文件系统。 bs是每次传递的数据大小。 注意:接…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...



