Leetcode刷题笔记2:数组基础2
导语
leetcode刷题笔记记录,本篇博客记录数组基础1部分的题目,主要题目包括:
- 977.有序数组的平方 ,
- 209.长度最小的子数组 ,
- 59.螺旋矩阵II
知识点
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。一般需要用到双指针来进行求解。
模拟
模拟并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。 需要对边界值和循环过程进行仔细的考虑。
Leetcode 977 有序数组的平方
题目描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入: nums = [-4,-1,0,3,10]
输出: [0,1,9,16,100]
解释: 平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入: nums = [-7,-3,2,3,11]
输出: [4,9,9,49,121]
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums已按 非递减顺序 排序
进阶:
- 请你设计时间复杂度为
O(n)的算法解决本问题
解法
可以使用双指针,从两边往中间走,这样会得到一个从大到小排列的数组,返回结果时只需要倒置一下就可以了。
class Solution(object):def sortedSquares(self, nums):""":type nums: List[int]:rtype: List[int]"""left, right = 0, len(nums) - 1ans_l = []while left <= right:if abs(nums[left]) >= abs(nums[right]):ans_l.append(nums[left] ** 2)left += 1else:ans_l.append(nums[right] ** 2)right -= 1return ans_l[::-1]
同时,也可以令双指针从中间开始(即从正负数分界处开始),为此,需要先找到正负数的分界线,代码如下:
class Solution(object):def sortedSquares(self, nums):""":type nums: List[int]:rtype: List[int]"""# 寻找分割点cut = -1for num in nums:if num < 0:cut += 1else:break# 这样cut右边都是非负数,左边都是负数left, right = cut, cut + 1ans_l = []while left>= 0 or right <= len(nums)-1:if left < 0:ans_l.append(nums[right] ** 2)right += 1elif right > len(nums) - 1:ans_l.append(nums[left] ** 2)left -= 1elif -nums[left] <= nums[right]:ans_l.append(nums[left] ** 2)left -= 1else:ans_l.append(nums[right] ** 2)right += 1return ans_l
Leetcode 209 长度最小的子数组
题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ****≥ target ****的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度 。 如果不存在符合条件的子数组,返回 0 。
示例 1:
输入: target = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入: target = 4, nums = [1,4,4]
输出: 1
示例 3:
输入: target = 11, nums = [1,1,1,1,1,1,1,1]
输出: 0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
解法
最简单的解法为暴力解法,但Leetcode上已经提示,Python的暴力解法一定会超时,所以这里使用滑动窗口来解决这个问题。
暴力解法中一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,那么滑动窗口如何用一个for循环来完成这个操作呢。
一个最关键的问题在于如果用一个for循环,那么应该表示滑动窗口的起始位置,还是终止位置?如果只用一个for循环来表示滑动窗口的起始位置,那么如何遍历剩下的终止位置?此时难免再次陷入暴力解法的怪圈。所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
滑动窗口解法
class Solution(object):def minSubArrayLen(self, target, nums):""":type target: int:type nums: List[int]:rtype: int"""start, ans = 0, 0min_length = len(nums) + 1for end in range(len(nums)):ans += nums[end]while ans >= target:min_length = min(end-start+1, min_length)ans -= nums[start]start += 1return min_length if min_length <= len(nums) else 0
Leetcode 59 螺旋矩阵II
题目描述
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
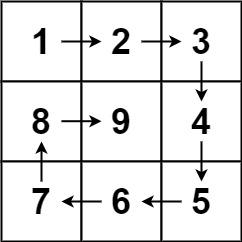
输入: n = 3
输出: [[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入: n = 1
输出: [[1]]
提示:
1 <= n <= 20
解法
这个题目的过程就是模拟,需要考虑好边界值条件,一个解题的关键是处理好区间选取,为了代码统一和边界值统一考虑,应选取左开右闭的区间,即每一行列都只考虑起始位置点,而不考虑终止位置点。
代码如下:
class Solution(object):def generateMatrix(self, n):""":type n: int:rtype: List[List[int]]"""matrix = [[0] * n for j in range(n)]cnt = 1offset = 1start_x, start_y =0, 0loop = n // 2while loop:for j in range( start_y, n - offset ):matrix[start_x][j] = cntcnt += 1for i in range( start_x, n - offset ):matrix[i][n-offset] = cntcnt += 1for j in range( n - offset, start_y, -1):matrix[n-offset][j] = cntcnt += 1for i in range( n - offset, start_x, -1):matrix[i][start_y] = cntcnt += 1start_x += 1start_y += 1offset += 1loop -= 1if n%2 == 1:matrix[n//2][n//2] = n * n return matrix参考
- 代码随想录
- 题解
相关文章:

Leetcode刷题笔记2:数组基础2
导语 leetcode刷题笔记记录,本篇博客记录数组基础1部分的题目,主要题目包括: 977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵II 知识点 滑动窗口 所谓滑动窗口,就是不断的调节子序列的起始位…...
)
整理好了!2024年最常见 20 道 Redis面试题(八)
上一篇地址:整理好了!2024年最常见 20 道 Redis面试题(七)-CSDN博客 十五、Redis 的性能调优有哪些方法? Redis的性能调优是一个多方面的工作,涉及到硬件、配置、代码层面的优化等多个方面。以下是一些常…...
)
【STM32项目】基于stm32智能鱼缸控制系统的设计与实现(完整工程资料源码)
实物演示效果 基于stm32智能鱼缸控制系统的设计与实现 目录: 实物演示效果 目录: 一、 绪论...
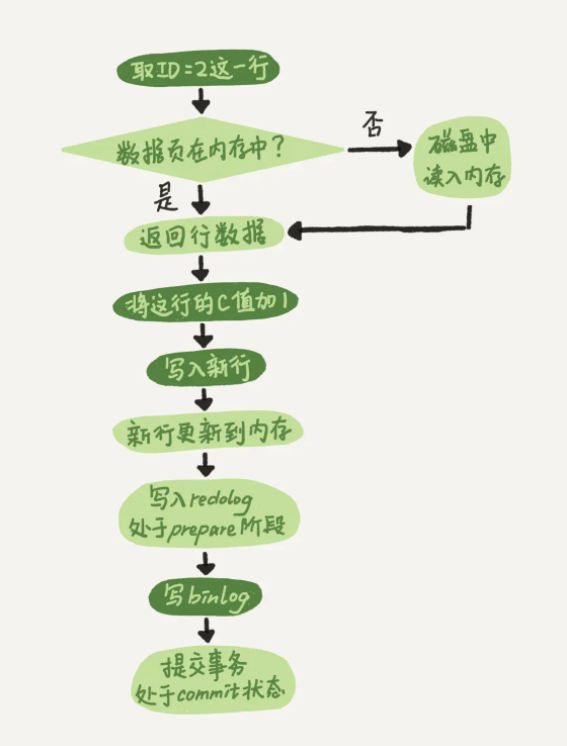
深入理解 Mysql 分层架构:从存储引擎到查询优化器的内部机制解析
一、基础架构 1.连接器 1.会先连接到这个数据库上,这时候接待你的就是连接器。连接器负责跟客户端建立连接、获取权限、维持和管理连接 2.用户密码连接成功之后,会从权限表中拿出你的权限,后续操作权限都依赖于此时拿出的权限,这就意味着当链…...
Java筑基(三)
Java筑基(三) 一、final概念1、案例1:采用继承:2、案例2:final修饰的类不可以被继承:3、案例3:final修饰的类不能有子类,但是可以有父类4、final修饰构造方法5、final修饰普通方法6、…...
Zoho Campaigns邮件营销怎么发邮件?
Zoho Campaigns,作为业界领先的邮件营销平台,以其强大的功能、用户友好的界面以及深度的分析能力,为企业提供了一站式的邮件营销解决方案,助力企业高效地触达目标受众,构建并巩固庞大的客户基础。云衔科技为企业提供Zo…...

Qt 界面上字体自适应控件大小 - 随控件缩放
Qt 界面上字体自适应控件大小 - 随控件缩放 引言一、设计思路二、进阶版大致思路三、参考链接 引言 Qt控件自适应字体大小可以用adjustSize()函数,但字体自适应控件大小并没有现成的函数可调. - 本文实现了按钮上的字体随按钮大小变化而变化 (如上图所示) - 其他控件…...

【Python】 使用SMOTE解决数据不平衡问题
原谅把你带走的雨天 在渐渐模糊的窗前 每个人最后都要说再见 原谅被你带走的永远 微笑着容易过一天 也许是我已经 老了一点 那些日子你会不会舍不得 思念就像关不紧的门 空气里有幸福的灰尘 否则为何闭上眼睛的时候 又全都想起了 谁都别说 让我一个人躲一躲 你的承诺 我竟然没怀…...
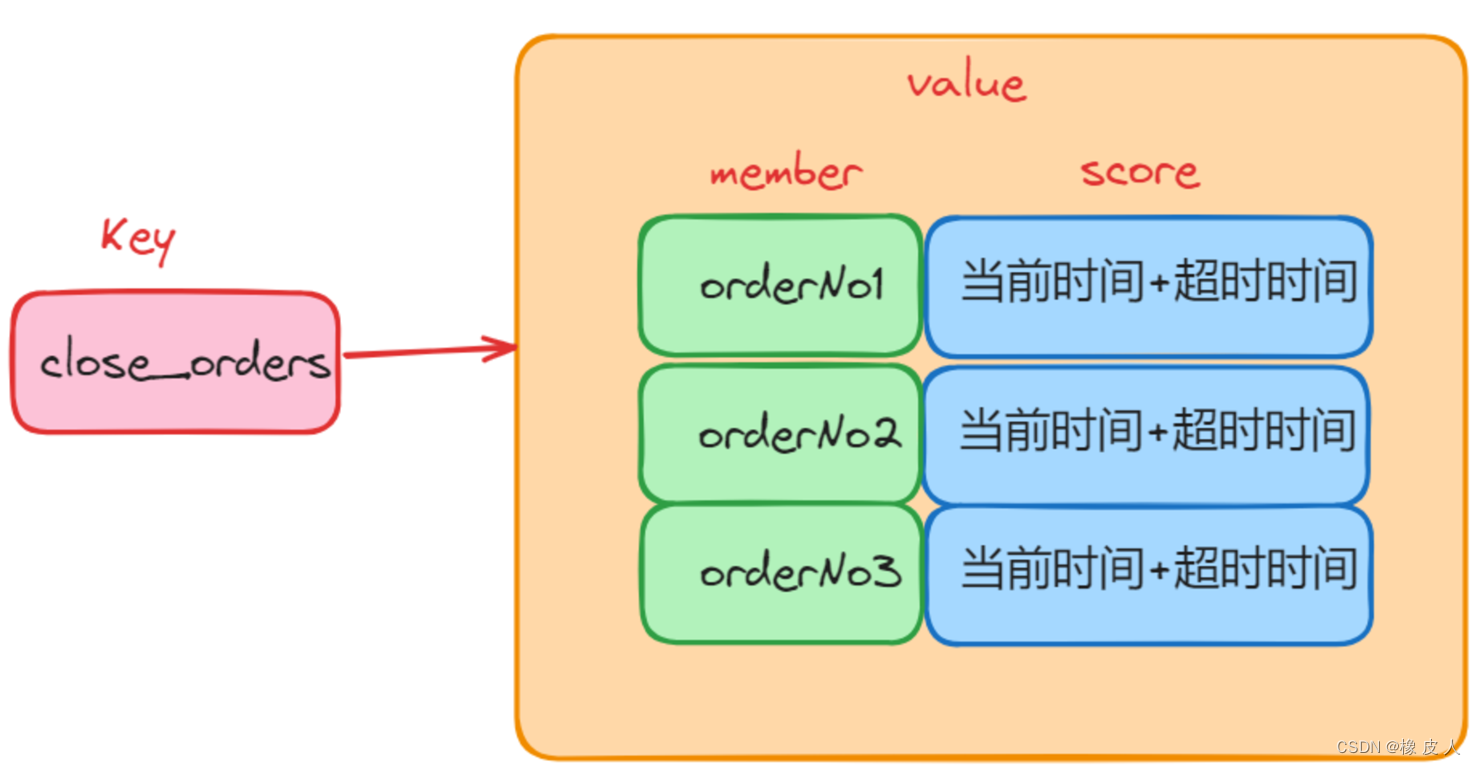
Redis第18讲——Redis和Redission实现延迟消息
即使不是做电商业务的同学,也一定知道订单超时关闭这种业务场景,这个场景大致就是用户下单后,如果在一定时间内未支付(比如15分钟、半小时),那么系统就会把这笔订单给关闭掉。这个功能实现的方式有很多种&a…...
返回枚举类给前端
1. 前言 在实际开发过程中,前端的下拉框或者单选按钮的内容通常的需要和后端匹配的,故一般会由后端将下拉框的内容或单选框的内容传给前端,而这些内容在后端一般是由枚举类存储的,如果后端直接返回枚举类,返回结果将会…...

A. Maximize?
time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output You are given an integer x𝑥. Your task is to find any integer y𝑦 (1≤y<x)(1≤𝑦<𝑥) su…...

RBAC 动态权限
文章目录 前言一、RBAC(Role-Based Access Control,基于角色的访问控制)二、Java实现RBAC 权限的大概思路1. 添加依赖2. 配置MyBatis-Plus和数据源1. 添加依赖2. 实体类与Mapper接口UserMapper.java 3. 配置MyBatis-Plus4. 自定义UserDetails…...
c语言:模拟strlen(三种方法)最全版本
1.计数的方法 #include <stdio.h> #include <assert.h> int my_strlen(const char * str)//const的使用优化 {int count0;assert(str)while(*str){count;str;}return count; } 2.用指针的方法(指针-指针) #include <stdio.h> #incl…...

线性模型--普通最小二乘法
线性模型 一、模型介绍二、用于回归的线性模型2.1 线性回归(普通最小二乘法) 一、模型介绍 线性模型是在实践中广泛使用的一类模型,该模型利用输入特征的线性函数进行预测。 二、用于回归的线性模型 以下代码可以在一维wave数据集上学习参…...
移动云以深度融合之服务,令“大”智慧贯穿云端
移动云助力大模型,开拓创新领未来。 云计算——AI模型的推动器。 当前人工智能技术发展的现状和趋势,以及中国在人工智能领域的发展策略和成就。确实,以 ChatGPT 为代表的大型语言模型在自然语言处理、文本生成、对话系统等领域取得了显著的…...

簡述vue常用指令
Vue.js 提供了许多内置指令,这些指令用于在模板中添加特殊功能。以下是一些 Vue 的常用内置指令的简要说明: v-text: 更新元素的 textContent。示例:<span v-text"message"></span> v-html: 更…...

【建议收藏】用AI快速生成一个网页(名侦探柯南~灰原哀主题网页),适合大学生web期末大作业
下面是提供给AI的提示词和AI给出的代码以及成果展示 1、生成一个网页导航栏,宽度为1300px,高度为60px。导航区域在导航栏最右侧不超出导航栏,高60px,宽度500px,里面是5个导航菜单项横向排列,每个宽度100px&…...

用c++用4个凸函数(觉得啥好用用啥)去测试adam,rmsprop,adagrad算法的性能(谁先找到最优点)
为了测试 Adam、RMSProp 和 Adagrad 算法的性能,你可以使用四个凸函数进行实验。以下是一些常用的凸函数示例: Rosenbrock 函数: Booth 函数: Himmelblau 函数: Beale 函数: 你可以选择其中一个或多…...
AJAX初级
AJAX的概念: 使用浏览器的 XMLHttpRequest 对象 与服务器通信 浏览器网页中,使用 AJAX技术(XHR对象)发起获取省份列表数据的请求,服务器代码响应准备好的省份列表数据给前端,前端拿到数据数组以后…...

重载大于号运算符,比较复数大小
本题目要求编写代码的功能为: 输入两个复数(变量名自拟),比较复数模的大小,复数实部与虚部都是整数 要求输入时输入4个整数,分别代表复数1的实部、虚部,复数2的实部虚部 输入格式: 在同一行中输…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
