R实验 方差分析
实验目的：
掌握单因素方差分析的思想和方法；
掌握多重均值检验方法；
掌握多个总体的方差齐性检验；
掌握Kruskal-Wallis秩和检验的思想和方法；
掌握多重Wilcoxon秩和检验的思想和方法。
实验内容：
（习题7.1）进行一次试验，当缓慢旋转的布面轮子受到磨损时，比较3种布上涂料的磨损量。对每种涂料类型试验10个涂料样品，记录每个样品直到出现可见磨损时的小时数，数据由下表给出（数据存放在paint.data文件中）。试用单因素方差分析方法分析：这3种涂料直至磨损明显可见的平均时间是否存在显著差异？如果存在，请做多重T检验，分析哪种涂料之间存在显著差异。
| 涂料 | 磨损小时数 | |||||||||
| A | 148 | 76 | 393 | 520 | 236 | 134 | 55 | 166 | 415 | 153 |
| B | 513 | 264 | 433 | 94 | 535 | 327 | 214 | 135 | 280 | 304 |
| C | 335 | 643 | 216 | 536 | 128 | 723 | 258 | 380 | 594 | 465 |
三种涂料的磨损数据
解：
（1）这3种涂料直至磨损明显可见的平均时间是否存在显著差异？
提出假设：
H0：3种涂料直至磨损明显可见的平均时间不存在显著差异。
H1：3种涂料直至磨损明显可见的平均时间存在显著差异。
源代码及运行结果：（复制到此处，不要截图）
> x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\paint.data")Read 30 items> A<-factor(rep(1:3,c(10,10,10)))> paint.aov<-aov(x~A)> summary(paint.aov)Df Sum Sq Mean Sq F value Pr(>F)
A 2 198772 99386 3.482 0.0452 *
Residuals 27 770671 28543
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
结论：P值（0.0452＜0.05），拒绝原假设，即3种涂料直至磨损明显可见的平均时间存在显著差异。
（2）如果存在，请做多重T检验，分析哪种涂料之间存在显著差异？
提出假设：
H0：μi＝μj i，j＝1，2，3，i≠j
H1：μi≠μj i，j＝1，2，3，i≠j
源代码及运行结果：（复制到此处，不要截图）
> x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\paint.data")> A<-factor(rep(1:3,c(10,10,10)))> tapply(x,A,mean)1 2 3
229.6 309.9 427.8
> pairwise.t.test(x,A)Pairwise comparisons using t tests with pooled SD
data: x and A
1 2
2 0.297 -
3 0.042 0.261
P value adjustment method: holm
结论：由结果得出，A涂料与B涂料有显著性差异和C涂料没有显著性差异，B涂料与C涂料有显著性差异。
（习题7.2）用于清洁金属部件有3种有机溶剂：芬芳剂、氯烷和酯类。下表（数据存放在solvent.data文件中）给出了这3种溶剂吸附比的测试结果，能否根据这组数据分析出这3种溶剂的吸附比是否存在显著差异？如果存在，请做多重T检验，分析哪种有机溶剂之间存在显著差异。
| 溶剂 | 摩尔分数 | ||||||||
| 芬芳剂 | 1.06 | 0.79 | 0.82 | 0.89 | 1.05 | 0.95 | 0.65 | 1.15 | 1.12 |
| 氯烷 | 1.58 | 1.45 | 0.57 | 1.16 | 1.12 | 0.91 | 0.83 | 0.43 | |
| 酯类 | 0.29 | 0.06 | 0.44 | 0.61 | 0.55 | 0.43 | 0.51 | 0.10 | 0.34 |
| 0.53 | 0.06 | 0.09 | 0.17 | 0.60 | 0.17 | ||||
三种溶剂吸附比数据（单位：摩尔分数）
解：
（1）这3种溶剂的吸附比是否存在显著差异？
提出假设：
H0：3种溶剂的吸附比不存在显著差异
H1：3种溶剂的吸附比存在显著差异
源代码及运行结果：（复制到此处，不要截图）
> solvent<-data.frame(x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\solvent.data"),+ A<-factor(rep(1:3,c(9,8,15))))Read 32 items
> solvent.aov<-aov(x~A,data = solvent)> summary(solvent.aov)Df Sum Sq Mean Sq F value Pr(>F)
A 2 3.305 1.6527 24.51 5.86e-07 ***
Residuals 29 1.955 0.0674
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
结论：P值远小于0.01，因此拒绝原假设，即3种溶剂的吸附比存在显著差异。
（2）如果存在，请做多重T检验，分析哪种有机溶剂之间存在显著差异？
提出假设：
H0：μi＝μj i，j＝1，2，3，i≠j
H1：μi＝μj i，j＝1，2，3，i≠j
源代码及运行结果：（复制到此处，不要截图）
> attach(solvent)The following objects are masked from solvent (pos = 3):
A....factor.rep.1.3..c.9..8..15...,
x....scan..C...Users..黄培滇..Desktop..R语言生物统计学..chap07..solvent.data..
> tapply(x,A,mean)1 2 3
0.9422222 1.0062500 0.3300000
> pairwise.t.test(x,A)Pairwise comparisons using t tests with pooled SD
data: x and A
1 2
2 0.62 -
3 9.8e-06 5.5e-06
P value adjustment method: holm
结论：由结果得出，芬芳剂与氯烷没有显著性差异，而与酯类有显著性差异；氯烷与酯类没有显著性差异。
（习题7.3）对习题7.2的数据做正态性检验和方差齐性检验，试分析：使用方差不同模型（如oneway.test()函数）和方差相同模型（如aov()函数）哪个更合理？
解：
（1）正态性检验
提出假设：
H0：a试剂服从正态性，a＝1，2，3
H1：a试剂不服从正态性，a＝1，2，3
源代码及运行结果：（复制到此处，不要截图）
>#直接引用上题构建好的数据表
> with(solvent,tapply(x,A,shapiro.test))$`1`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.9508, p-value = 0.6989
$`2`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.96815, p-value = 0.8831
$`3`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.89092, p-value = 0.06923
结论：从计算结果得出，3组数据服从正态性
（2）方差齐性检验
提出假设：
H0：数据服从方差齐性
H1：数据不服从方差齐性
源代码及运行结果：（复制到此处，不要截图）
> #直接引用构建好的solvent数据表> bartlett.test(x~A,data = solvent)Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 6.7779, df = 2, p-value =
0.03374
结论：P值（0.0337＜0.05），拒绝原假设，即数据不服从方差齐性。
（3）使用方差不同模型（如oneway.test()函数）和方差相同模型（如aov()函数）哪个更合理？
基于本题的情况即满足正态性，但不满足方差齐性，oneway,test()函数更合适。
（习题7.4）使用方差不同模型（oneway.test()函数）和秩检验方法（kruskal.test()函数）对习题7.1中的数据进行分析是否得到与习题7.1相同的结果？如果得到的结论不同，哪个结论更合理？试对数据做正态性检验（如shapiro.test()函数）和方差齐性检验（如bartlett.test()函数）来说明这一问题。
解：
（1）使用方差不同模型（oneway.test()函数）分析：这3种涂料直至磨损明显可见的平均时间是否存在显著差异？
提出假设：
H0：3种涂料直至磨损明显可见的平均时间不存在显著差异。
H1：3种涂料直至磨损明显可见的平均时间存在显著差异。
源代码及运行结果：（复制到此处，不要截图）
> paint<-data.frame(x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\paint.data"),+ A<-factor(rep(1:3,c(10,10,10))))Read 30 items
> oneway.test(x~A,data = paint)One-way analysis of means (not assuming equal
variances)
data: x and A
F = 2.9699, num df = 2.000, denom df = 17.775,
p-value = 0.07713
结论：P值（0.0771＞0.05），接受原假设，即3种涂料直至磨损明显可见的平均时间不存在显著差异。
（2）使用秩检验方法（kruskal.test()分析：这3种涂料直至磨损明显可见的平均时间是否存在显著差异？
提出假设：
H0：3种涂料直至磨损明显可见的平均时间不存在显著差异。
H1：3种涂料直至磨损明显可见的平均时间存在显著差异。
源代码及运行结果：（复制到此处，不要截图）
> kruskal.test(x~A,data = paint)Kruskal-Wallis rank sum test
data: x by A
Kruskal-Wallis chi-squared = 5.4684, df = 2, p-value
= 0.06495
结论：P值（0.06495＞0.05），接受原假设，即3种涂料直至磨损明显可见的平均时间不存在显著差异。
（3）如果得到的结论不同，哪个结论更合理？试对数据做正态性检验（如shapiro.test()函数）和方差齐性检验（如bartlett.test()函数）来说明这一问题。
> with(paint,tapply(x,A,shapiro.test))$`1`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.87975, p-value = 0.1296
$`2`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95268, p-value = 0.7003
$`3`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.97137, p-value = 0.9033
> bartlett.test(x~A,data = paint)Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 0.79406, df = 2, p-value =
0.6723
由计算结果可知，习题7.1数据服从正态性要求与方差齐性要求。因此采用方差分析更为合适
（习题7.6）考查不同职业人群对心理疾病原因的认识，现找到A、B、C3种职业的人员各10名，这30个人用笔试的方式回答心理疾病原因的知识问卷，测试分数如下表所示（数据存放在staff.data文件中）。(1)使用Kruskal-Walis秩和检验，分析这3种职业人员平均测试分数是否有显著差异；(2)使用正态性检验和方差齐性检验的方法来分析Kruskal-Wallis秩和检验的合理性。
| 职业 | 测试分数 | |||||||||
| A | 62 | 60 | 60 | 25 | 24 | 23 | 20 | 13 | 12 | 6 |
| B | 62 | 62 | 24 | 24 | 22 | 20 | 19 | 10 | 8 | 8 |
| C | 37 | 31 | 15 | 15 | 14 | 14 | 14 | 5 | 3 | 2 |
3种职业人员心理疾病的测试分析
解：
（1）使用Kruskal-Walis秩和检验，分析这3种职业人员平均测试分数是否有显著差异？
提出假设：
H0：3种职业人员平均测试分数没有显著差异
H1：3种职业人员平均测试分数有显著差异
源代码及运行结果：（复制到此处，不要截图）
> staff<-data.frame(x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\staff.data"),+ A<-factor(rep(1:3,c(10,10,10))))Read 30 items
> kruskal.test(x~A,data = staff)Kruskal-Wallis rank sum test
data: x by A
Kruskal-Wallis chi-squared = 3.2535, df = 2, p-value
= 0.1966
结论：P值（0.1966＞0.05）接受原假设，即3种职业人员平均测试分数没有显著差异。
（2）使用正态性检验和方差齐性检验的方法来分析Kruskal-Wallis秩和检验的合理性。
> with(staff,tapply(x,A,shapiro.test))$`1`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.81494, p-value = 0.02201
$`2`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.76284, p-value = 0.005115
$`3`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.86148, p-value = 0.07944
> bartlett.test(x~A,data = staff)Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 3.6228, df = 2, p-value =
0.1634
由计算结果，可以得出，题目中第1、2组数据不满足正态性要求，而数据满足方差齐性要求，因此Kruskal-Wallis秩和检验符合该题目。
（习题7.7）生物学家认为，河流中的富营养水注入海湾后，会导致浮游生物赖以生存的藻类快速生长，细菌则以浮游生物的排泄物和死藻类为主，消耗了水中的氧。为验证是否有这种情况发生，现测试某河流入海口开始的4个海洋区域中的平均溶解氧含量（见下表，.数据存放在sea.data文件中）。(1)对数据做正态性检验和方差齐性检验；(2)4个海洋区域溶解氧含量是否有显著差异？(3)如果有差异，哪些区域之间有差异？（注：请根据(1)的结果合理选择检验的方法）
| 距入海口距离 | 溶解氧含量 | |||||||||
| 1km | 1 | 5 | 2 | 1 | 2 | 2 | 4 | 3 | 0 | 2 |
| 5km | 4 | 8 | 2 | 3 | 8 | 5 | 6 | 4 | 3 | 3 |
| 10km | 20 | 26 | 24 | 11 | 28 | 20 | 19 | 19 | 21 | 24 |
| 20km | 37 | 30 | 26 | 24 | 41 | 25 | 36 | 31 | 31 | 33 |
离入海口处4个距离的平均溶解氧含量（单位：mg/L）
解：
（1）对数据做正态性检验和方差齐性检验
①正态性检验。提出假设：
H0：a km数据服从正态性，a = 1，5，10，20
H1：a km数据不服从正态性，a = 1，5，10，20
源代码及运行结果：（复制到此处，不要截图）
> sea<-data.frame(x<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap07\\sea.data"),+ A<-factor(rep(1:4,c(10,10,10,10))))Read 40 items
> with(sea,tapply(x,A,shapiro.test))$`1`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.93644, p-value = 0.5141
$`2`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.88391, p-value = 0.1446
$`3`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.92543, p-value = 0.4045
$`4`
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95791, p-value = 0.7618
结论：由计算结果可以得出，数据都服从正态性。
②方差齐性检验。提出假设：
H0：数据服从方差齐性
H1：数据不服从方差齐性
源代码及运行结果：（复制到此处，不要截图）
> bartlett.test(x~A,data = sea)Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 17.17, df = 3, p-value =
0.000652
结论：P值小于0.05，拒绝原假设，即数据不服从方差齐性
（2）4个海洋区域溶解氧含量是否有显著差异？（用单因素方差分析还是Kruskal-Wallis检验？）提出假设：
由于数据服从正态性，但不满足方差齐性，因此采用单因素方差分析中的oneway.test()函数
H0：4个海洋区域溶解氧含量无显著差异
H1：4个海洋区域溶解氧含量有显著差异
源代码及运行结果：（复制到此处，不要截图）
> oneway.test(x~A,data = sea)One-way analysis of means (not assuming equal
variances)
data: x and A
F = 118.54, num df = 3.000, denom df = 18.315,
p-value = 3.503e-12
结论：P值远小于0.01，拒绝原假设，即4个海洋区域溶解氧含量有显著差异。
（3）如果有差异，哪些区域之间有差异？
> tapply(x,A,mean)1 2 3 4
2.2 4.6 21.2 31.4
> pairwise.t.test(x,A)Pairwise comparisons using t tests with pooled SD
data: x and A
1 2 3
2 0.17 - -
3 1.8e-12 5.2e-11 -
4 < 2e-16 < 2e-16 1.8e-06
P value adjustment method: holm
由计算结果，得出1区域和2区域之间没有显著性差异与其他区域有显著性差异，而其余区域彼此之间都纯在显著性差异。
思考：
方差分析使用的前提条件有哪三个？
方差齐性
正态性
独立性
设因素A有r个水平，所有样本数据的总数为n，则组间平方和SA的自由度是多少？组内平方和SE的自由度是多少？
组间平方和自由度为r-1，组内平方和自由度为r-n。
R语言中，要给出完整的方差分析表，需要用到哪两个函数？
aov() 与 summary()
方差分析的统计量F=（ A ）。
A. SA/SE B. MSA/MSE C. MSE/MSA D. SE/SA
所有样本数据与所有样本数据的均数之差的平方和称为___总平方和________。
当数据只满足正态性，但不满足方差齐性时，可用_____oneway.test()____________函数做方差分析。
单因素方差分析时，如果拒绝原假设，想进一步了解到底哪些总体之间的均值有显著性差异，可以做多重T检验，R软件中，用于此检验的函数是_____paiewise.t.test()________。
Kruskal-Wallis秩和检验是用于______数据既不满足正态性要求，又不满足方差齐性要求________情况下的非参数检验。
Kruskal-Wallis秩和检验时，如果拒绝原假设，想进一步了解到底哪些总体之间的有显著性差异，由于此时没有正态性和方差齐性的条件，因此需要做多重Wilcoxon检验，R软件中，用于此检验的函数是____pairwise.wilcox.test()_________。
相关文章：
R实验 方差分析
实验目的： 掌握单因素方差分析的思想和方法； 掌握多重均值检验方法； 掌握多个总体的方差齐性检验； 掌握Kruskal-Wallis秩和检验的思想和方法； 掌握多重Wilcoxon秩和检验的思想和方法。 实验内容： &…...
AI智能体｜手把手教你使用扣子Coze图像流的文生图功能
大家好，我是无界生长。 AI智能体｜手把手教你使用扣子Coze图像流的文生图功能本文详细介绍了Coze平台的\x26quot;图像流\x26quot;功能中的\x26quot;文生图\x26quot;节点，包括创建图像流、编排文生图节点、节点参数配置，并通过案例…...
应用程序图标提取
文章目录 [toc]提取过程提取案例——提取7-zip应用程序的图标 提取过程 找到需要提取图标的应用程序的.exe文件 复制.exe文件到桌面，并将复制的.exe文件后缀改为.zip 使用解压工具7-zip解压.zip文件 在解压后的文件夹中，在.rsrc/ICON路径下的.ico文件…...
Excel表格在线解密：轻松解密密码，快速恢复数据
忘记了excel表格密码？教你简单两步走：具体步骤如下。首先，在百度搜索中键入“密码帝官网”。其次，点击“立即开始”，在用户中心上传表格文件即可找回密码。这种方法不用下载软件，操作简单易行，适…...
springboot小结1
什么是springboot Spring Boot是为了简化Spring应用的创建、运行、调试、部署等而出现的，使用它可以做到专注于Spring应用的开发，而无需过多关注XML的配置。 简单来说，它提供了一堆依赖打包Starter，并已经按照使用习惯解决…...
【Qt 学习笔记】Qt窗口 | 菜单栏 | QMenuBar的使用及说明
博客主页：Duck Bro 博客主页系列专栏：Qt 专栏关注博主，后期持续更新系列文章如果有错误感谢请大家批评指出，及时修改感谢大家点赞👍收藏⭐评论✍ Qt窗口 | 菜单栏 | QMenuBar的使用及说明 文章编号：Qt 学习…...
Spark运行模式详解
Spark概述 Spark 可以在多种不同的运行模式下执行，每种模式都有其自身的特点和适用场景。 部署Spark集群大体上分为两种模式：单机模式与集群模式。大多数分布式框架都支持单机模式，方便开发者调试框架的运行环境。但是在生产环境中ÿ…...
vcpkg环境配置
vcpkg 使用linux相关库，设置环境变量VCPKG_ROOT，设置cmake工具链$VCPKG_ROOT/scripts\buildsystems\vcpkg.cmake set VCPKG_DEFAULT_TRIPLETx64-windows .\vcpkg.exe install fftw3 freetype gettext glibmm gtkmm libjpeg-turbo libpng libxmlpp libs…...
python学习：基础语句
目录 条件语句 循环语句 for 循环 while 循环 break continue 条件语句 Python提供了 if、elif、else 来进行逻辑判断。格式如下： Pythonif 判断条件1: 执行语句1... elif 判断条件2: 执行语句2... elif 判断条件3: 执行语句3... else: 执行语句4…...
Nginx限制IP访问详解
在Web服务器管理中，限制某些IP地址访问网站是一个常见的需求。Nginx作为一款高性能的HTTP服务器和反向代理服务器，提供了灵活强大的配置选项来实现这一功能。本文将详细讲解如何在Nginx中限制IP访问，并通过示例代码展示具体操作。 一、Nginx…...
Three.js——二维平面、二维圆、自定义二维图形、立方体、球体、圆柱体、圆环、扭结、多面体、文字
个人简介 👀个人主页： 前端杂货铺 ⚡开源项目： rich-vue3 （基于 Vue3 TS Pinia Element Plus Spring全家桶 MySQL） 🙋♂️学习方向： 主攻前端方向，正逐渐往全干发展 …...
24年湖南教资认定即将开始，别被照片卡审！
24年湖南教资认定即将开始，别被照片卡审！...
数据库（8）——DML数据操作
增添数据 给指定字段添加数据 INSERT INTO 表名 (字段名1，字段名2,...)VALUES(值1,值2...); 没有的添加的字段默认为NULL。 给全部字段添加数据 INSERT INTO 表名 VALUE (值1,值2,....值n); 此时值的顺序对应表中字段的顺序 批量添加数据 INSERT INTO 表名(字段1,…...
Gitee在已有项目基础上创建仓库中遇到的问题和解决
问题一：fatal: remote origin already exists 解释：当前仓库添加了一个名为"origin"的远程仓库配置，此时输入 git remote add origin https://xxx就会提示上面的内容。 解决方案1:移除旧的origin git remote remove origin 解决方案…...
【推荐算法-特征工程】每种item单侧特征，都可产生对应user单侧特征
比如item的平均成单价格，可以分成10个档位，作为一个标签值打在item上， 那么对应user对item的click用户行为，就能产生user-click的10个档位作为特征值 作为user的标签。 比如item的平均点击率，也可以分成比如20个档位…...
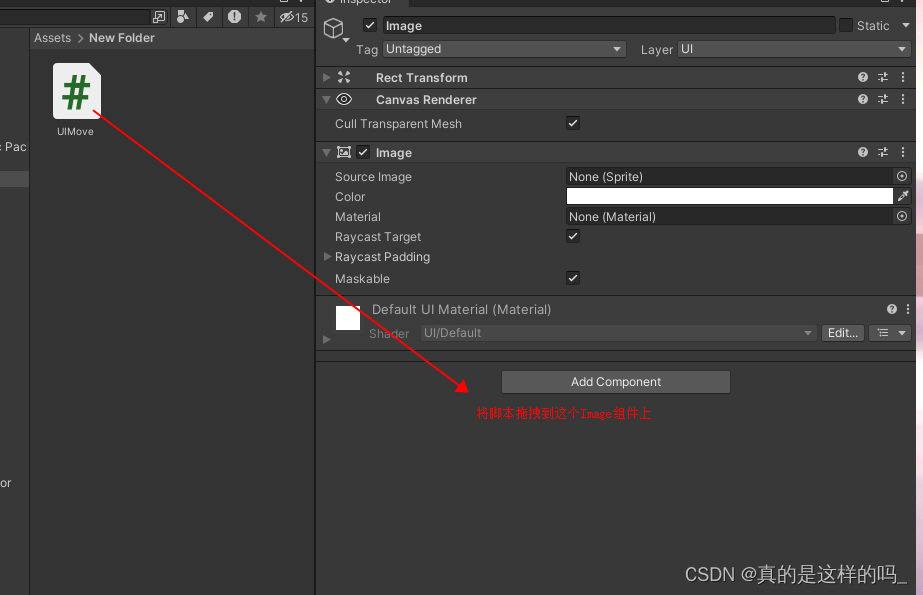
一行代码实现UI拖拽的效果
演示 先来看效果吧！ 实现方式 1.首先创建一个你想拖动的UI图片 2.创建一个C#的脚本 3.编写控制脚本（代码按我的敲就行） 付上代码片段 public void OnDrag(PointerEventData eventData){transform.position eventData.position;} 4.添加脚…...
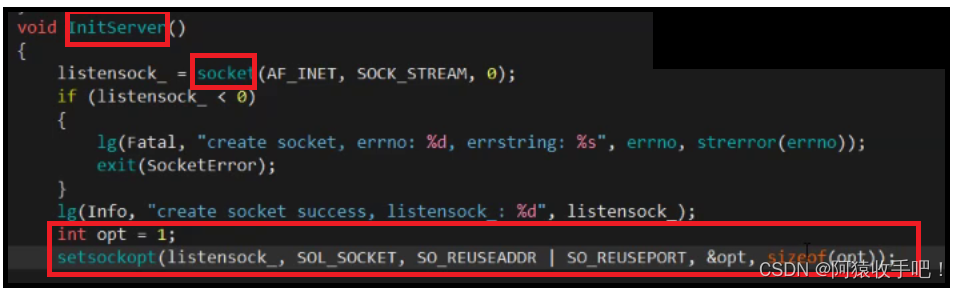
【Linux】TCP协议【下一】{三次握手/四次挥手的深度解读==状态变化}
文章目录 本篇知识需要有TCP协议【中】的知识！详情点击👇1.测试一：服务器start函数不定义任何行为（不调用accept）的三次握手状态变化int listen(int sockfd, int backlog);的backlog参数全连接队列当全连接队列已满&am…...
【C语言回顾】编译和链接
前言1. 编译2. 链接结语 上期回顾: 【C语言回顾】文件操作 个人主页：C_GUIQU 归属专栏：【C语言学习】 前言 各位小伙伴大家好！上期小编给大家讲解了C语言中的文件操作，接下来我们讲解一下编译和链接！ 1. 编译 预处理…...
2024年5月27日 十二生肖 今日运势
小运播报：2024年5月27日，星期一，农历四月二十 （甲辰年己巳月辛卯日），法定工作日。 红榜生肖：羊、蛇、狗 需要注意：鼠、鸡、龙 喜神方位：西南方 财神方位：…...
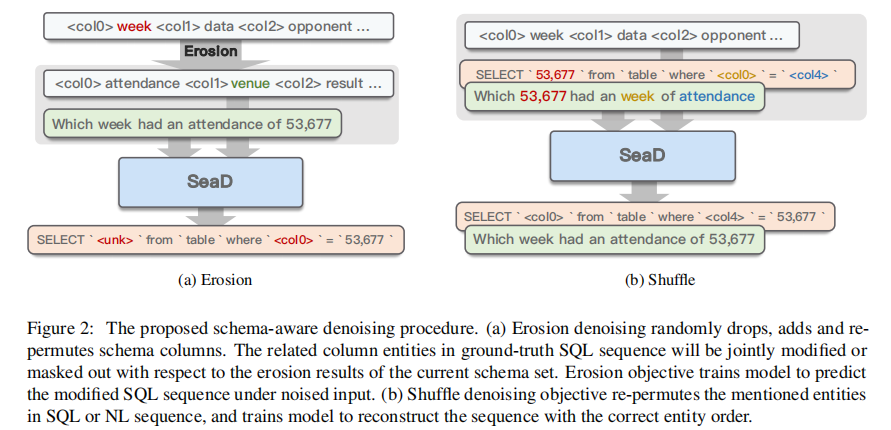
【Text2SQL 论文】SeaD：使用 Schema-aware 去噪训练的 end2end 的 Text2SQL
论文：SeaD: End-to-end Text-to-SQL Generation with Schema-aware Denoising ⭐⭐ NAACL 2022, arXiv:2105.07911 本论文提出 SeaD 模型，使用 schema-aware 的去噪方法来训练一个 end2end、seq2seq 的 Transformer 模型来实现 Text2SQL。 一、论文速读…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装（Encapsulation） 定义：将数据（属性）和操作数据的方法绑定在一起，通过访问控制符（private、protected、public）隐藏内部实现细节。示例： public …...
反向工程与模型迁移：打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下，商品详情API作为连接电商平台与开发者、商家及用户的关键纽带，其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息（如名称、价格、库存等）的获取与展示，已难以满足市场对个性化、智能…...
无法与IP建立连接，未能下载VSCode服务器
如题，在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈，发现是VSCode版本自动更新惹的祸！！！ 在VSCode的帮助->关于这里发现前几天VSCode自动更新了，我的版本号变成了1.100.3 才导致了远程连接出…...
使用分级同态加密防御梯度泄漏
抽象 联邦学习 （FL） 支持跨分布式客户端进行协作模型训练，而无需共享原始数据，这使其成为在互联和自动驾驶汽车 （CAV） 等领域保护隐私的机器学习的一种很有前途的方法。然而，最近的研究表明&…...
ESP32读取DHT11温湿度数据
芯片：ESP32 环境：Arduino 一、安装DHT11传感器库 红框的库，别安装错了 二、代码 注意，DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 （一）多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如，当用户上传一张“蓝色连衣裙”的图片时，接口可自动提取图像中的颜色（RGB值&…...
什么是库存周转？如何用进销存系统提高库存周转率？
你可能听说过这样一句话： “利润不是赚出来的，是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业，很多企业看着销售不错，账上却没钱、利润也不见了，一翻库存才发现： 一堆卖不动的旧货…...
C++ 求圆面积的程序（Program to find area of a circle）
给定半径r，求圆的面积。圆的面积应精确到小数点后5位。 例子： 输入：r 5 输出：78.53982 解释：由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982，因为我们只保留小数点后 5 位数字。 输…...
自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元（GRU）长短期记忆神经网络（LSTM）…...
如何在最短时间内提升打ctf（web)的水平？
刚刚刷完2遍 bugku 的 web 题，前来答题。 每个人对刷题理解是不同，有的人是看了writeup就等于刷了，有的人是收藏了writeup就等于刷了，有的人是跟着writeup做了一遍就等于刷了，还有的人是独立思考做了一遍就等于刷了。…...