【数据结构】二叉树-堆(上)

个人主页~
二叉树-堆
- 一、树的概念及结构
- 1、概念
- 2、相关概念
- 3、树的表示
- 4、树的实际应用
- 二、二叉树的概念和结构
- 1、概念
- 2、特殊二叉树
- 3、二叉树的性质
- 4、二叉树的存储结构
- (1)顺序存储
- (2)链式存储
- 三、二叉树的顺序结构以及实现
- 1、二叉树的顺序结构
- 2、堆的概念及结构
- (1)小根堆
- (2)大根堆
- 3、堆的实现
- (1)堆的向上调整算法--堆的创建
- ①一般方法
- ②向上调整建堆
- (2)向上调整算法的时间复杂度
- (3)向下调整算法维护堆
- (4)向下调整算法的时间复杂度
一、树的概念及结构
在我们学习二叉树之前,我们先要了解一下树的概念,二叉树就是一种树
1、概念
树是一种非线性的数据结构,它是由n个有限节点组成一个具有层次关系的集合,因为根据它所画出的抽象图看起来像一棵倒挂着的树,它的根朝上,树叶朝下
一棵树最顶上的节点叫做根节点,一棵树有且只有一个根节点,根节点没有前驱节点也就是说根节点上面就没有节点了
除了根节点以外,其余节点被分成N个互不相交的集合,我们形象的来说,就是一棵树的叶子和树枝是多对一的概念,也就是说一个树枝可以有多个叶子或者没有叶子,但是一个叶子只能长在一个树枝上,一条小树枝只能长在一条大树枝上,所以树是递归定义的
2、相关概念
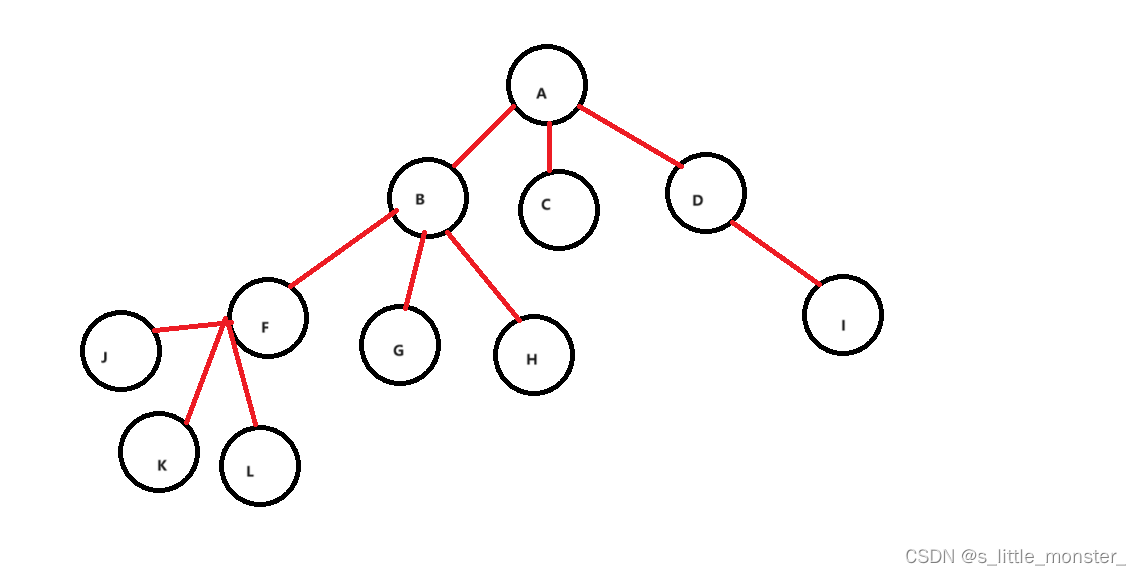
节点的度:一个节点含有子树的个数(A的度是3,C的度是0)
叶节点(终端节点):度为0的节点称为叶节点(GHIJKL)
分支节点(非终端节点):度不为0的节点(ABDF)
子节点:一个节点含有的子树的根结点(B是A的子节点)
父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点(A是B的父节点)
兄弟节点:这里的兄弟指的是亲兄弟,也就是具有相同父节点的节点(BCD是兄弟节点)
树的度:整棵树的度是这棵树中的节点的度中最大的那个度(这棵树最大是3)
节点的层次:根为第一层,根的子节点为第二层,子节点的子节点为第
三层,以此类推(第一层:A;第二层:BCD;第三层:FGHI;第四层:JKL)
树的高度(深度):树中节点的最大层次(四层)
堂兄弟节点:父亲为同一层的节点(HI)
节点的祖先:从根到该节点所经分支上的所有节点(J节点的祖先是ABF)
子孙:以某节点为根的子树中任意节点都称为该节点的子孙(B-L都是A的子孙)
森林:由N棵(N>0)互不相交的树组成的集合称为森林
树的概念都是由人类的亲缘关系决定的,我们在记忆的时候可以结合我们人类的亲缘关系来记忆
3、树的表示
树的表示方法有很多种,如果我们再像以前一样定义一个结构体,其中存放指针和数据,那样就不行了,因为我们不知道一个节点有多少子树,这样就没办法定义树的节点的结构体,这里,我们有一个最好的办法就是左孩子右兄弟法
左孩子右兄弟法:
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点,也就是最左边的孩子struct Node* _pNextBrother; // 指向其下一个兄弟结点,就是右边第一个兄弟DataType _data; // 结点中的数据域
};
左孩子右兄弟法就是一个指针指向左边第一个孩子,右指针指向右边第一个兄弟

图画的不太好看,将就一下
红色的线是左孩子
蓝色的线是右兄弟
这样我们可以简洁并且快速地找到这棵树所有的分支
4、树的实际应用
文件系统的目录就是树的应用
E盘:
这里就是树的应用,文件系统的目录是用树的结构实现的
二、二叉树的概念和结构
1、概念
二叉树就是在树的基础上加上特殊
二叉树是由一个根节点加上一个左子树和一个右子树组成的
二叉树不存在度大于2的节点
二叉树是有序树,因为它的子树有左右之分,次序不能颠倒
2、特殊二叉树
(1)满二叉树
一个二叉树,如果每一个层的节点数都达到最大值,那么这个二叉树就是满二叉树
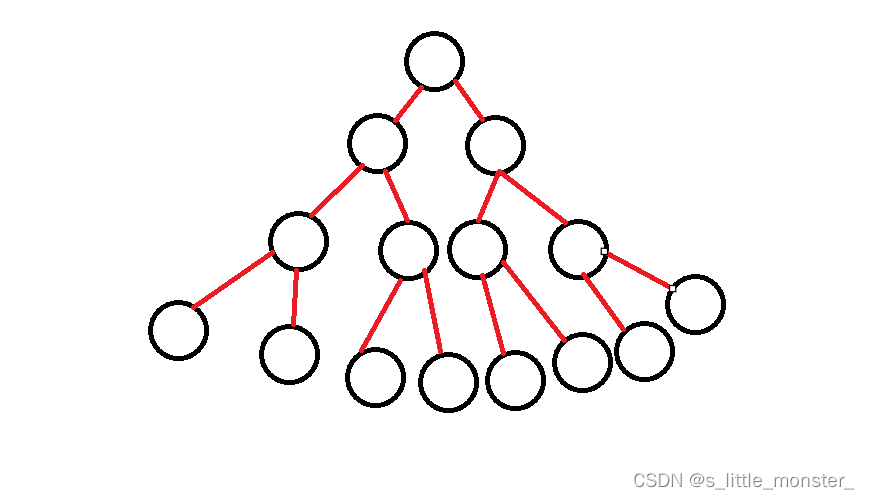
(2)完全二叉树
完全二叉树是效率很高的二叉树,它的最后一层可以不满,最后一层之前的层都是满的,然后最后一层的节点是需要按序排列的,满二叉树是一种特殊的完全二叉树
3、二叉树的性质
若规定根节点的层数为1,具有n个节点的满二叉树的深度h=log₂(n+1)
对于具有n个节点的完全二叉树,如果按照从上到下,从左到右的数组顺序对所有节点从0开始编号则对于序号为i的节点有如下几个性质:
①若i>0,i位置节点的父亲序号:(i-1)/2;i=0,i为根节点编号,无父亲节点
②若2i+1<n,左孩子序号为2i+1并且2i+1≥n,否则无左孩子
③若2i+2<n,右孩子序号为2i+2并且2i+2≥n,否则无右孩子
4、二叉树的存储结构
二叉树有两种存储结构,一种是顺序存储,另一种是链式存储
(1)顺序存储
顺序存储就是使用数组来存储,一般只适合表示完全二叉树,因为不是完全二叉树会有空间上的浪费,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
(2)链式存储
链式存储就是使用链表来存储,通常的方法是链表节点由三个域组成,分别是数据域以及左右指针域,左右指针存储左右孩子的地址
链式结构又分为二叉链和三叉链,这里使用的是二叉链
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* Left; // 指向左孩子struct BinTreeNode* Right; // 指向右孩子BTDataType data; // 值域
};// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* Parent; // 指向父节点struct BinTreeNode* Left; // 指向左孩子struct BinTreeNode* Right; // 指向右孩子BTDataType data; // 值域
};
三、二叉树的顺序结构以及实现
1、二叉树的顺序结构
现实中我们经常把堆(一种二叉树)使用顺序结构的数组来存储,这里的堆与malloc位置的堆的概念是不同的,malloc位置的堆是操作系统中的内存管理,这里的堆是我们人为实现的一种数据结构
2、堆的概念及结构
把一堆数据按照完全二叉树的顺序存储方式存储在一个一维数组中,并且满足第i项 ≤ 第2i+2项,i为自然数,则称为堆,根节点最大的堆叫大堆(大根堆),根节点最小的堆叫小堆(小根堆)
性质:
①堆总是一颗完全二叉树
②堆中某个节点的值总是不大于或不小于其父节点的值
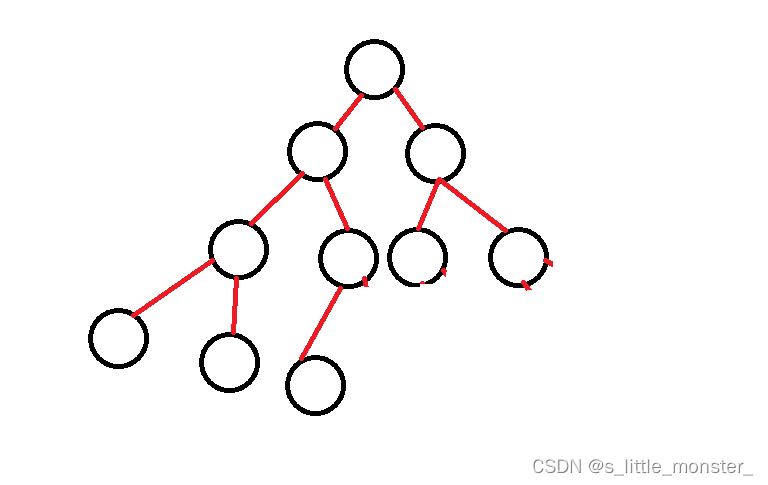
(1)小根堆
逻辑结构:
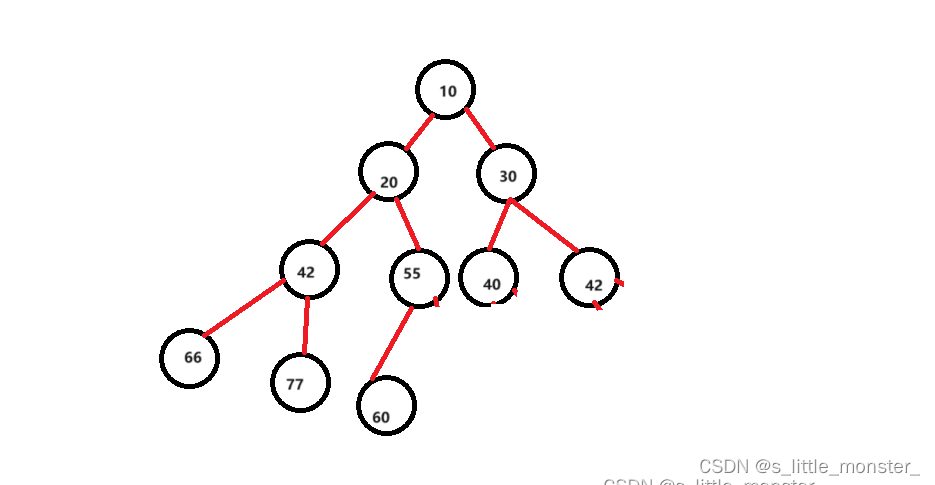
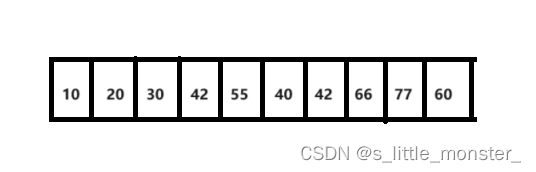
物理结构(存储结构):
(2)大根堆
逻辑结构:

物理结构(存储结构):

这里的存储结构中的数据不一定是有序的,也可以不是升序或者降序,但是大堆的父节点一定比子节点大,小堆的父节点一定比子节点小
3、堆的实现
(1)堆的向上调整算法–堆的创建
①一般方法
我们在使用堆的向下调整算法之前要保证左右子树都要是堆,那么在使用之前我们先要创建堆
我们创建一个数组,在逻辑上可以看做一颗完全二叉树,然后我们通过算法把它构建成为一个堆,从倒数第一个叶子节点开始调整一直到根节点,就可以调整成堆
int arr[] = {1,4,7,2,5,9};
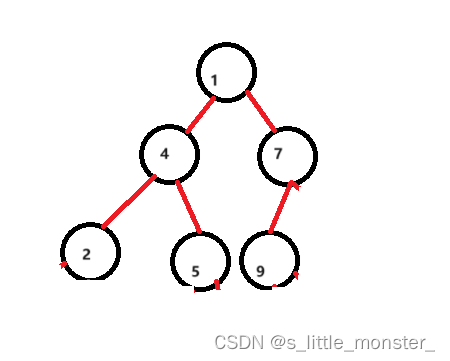
最后的9与它的父节点7交换:

1<9再交换

然后再检查最后一个叶子节点,重复上面的步骤,虽然这样最终可以建立一个堆,但这样效率特别低,所以我们有了向上调整算法来建堆
②向上调整建堆
现在我们有一个数组,在逻辑上看成一棵完全二叉树,我们要创建一个堆,可以用向上调整算法
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//因为除法向下取整,所以右孩子也能//因为是一颗完全二叉树,所以父节点总是可以通过子节点减1除以二找到//while (parent >= 0)while (child > 0)//这里用子节点作为循环条件,因为child可能调整到根节点上{if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}//大于就交换,把此时的父节点变成子节点,父节点的父节点变成父节点,比较上一层的关系else{break;}}
}
从二叉树的根节点的左孩子开始调整,按照下标依次调整,最终会建成一个堆
图演示:
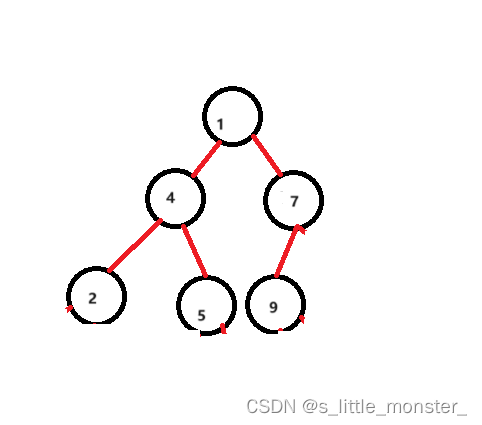
下标1向上调整:
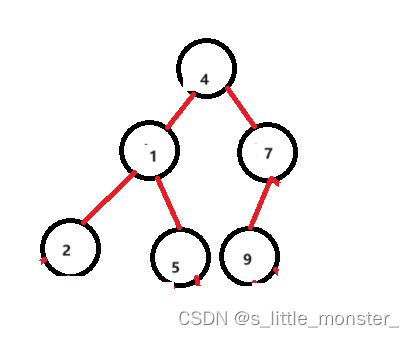
下标2向上调整:
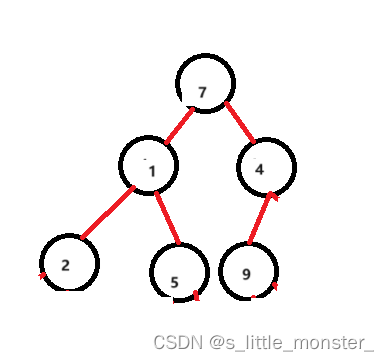
下标3调整两次:(第二次小于7,不调)

下标4调整两次:(第二次小于7,不调)

下标5调整两次:
第一次:

第二次:
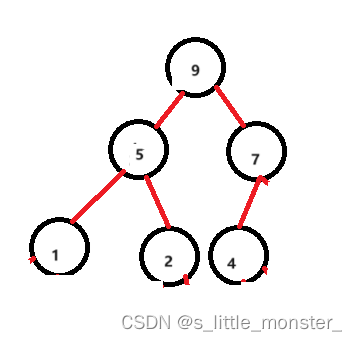
这样就建成一个堆了
(2)向上调整算法的时间复杂度

设树的高度为h
第1层:2^0个节点,需要向上移动0层
第2层:2^1个节点,需要向上移动1层
第3层:2^2个节点,需要向上移动2层
……
第h-1层:2^(h-2)个节点,需要向上移动h-2层
第h层:2^(h-1)个节点,需要向上移动h-1层
将它们相加
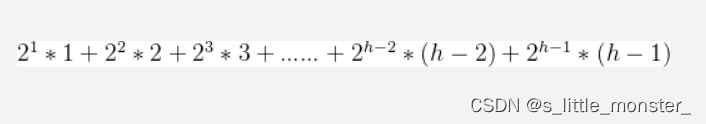
解得原式=2+2^h*(h-2)
遍历一遍为N = 2^h
去掉不重要的项,得时间复杂度O(N*log₂N)
(3)向下调整算法维护堆
当我们需要将堆顶的数据删除掉,那么这个堆就没有了根,如果再重新进行建堆会浪费很多的时间,这里有一种方法的时间复杂度小于重新建堆,这种算法就是向下调整算法
void AdjustDown(int* a, int n, int parent)//n是数组a的数据个数
{int child = parent * 2 + 1;//左孩子while (child < n){// 选出左右孩子中大的那个if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}//谁大谁是爹else{break;}}
}
(4)向下调整算法的时间复杂度

设树的高度为h
第1层:2^0个节点,需要向下移动h-1层
第2层:2^1个节点,需要向下移动h-2层
第3层:2^2个节点,需要向下移动h-3层
……
第h-1层:2^(h-2)个节点,需要向下移动1层
第h层:2^(h-1)个节点,需要向下移动0层
将它们相加之后由错位相减法得
2^h-1-h
因为N = 2^h,所以原式=N-1-log₂N
因为当h趋于无穷大时,N远大于log₂N,所以时间复杂度O(N)
今日分享就到这~

相关文章:

【数据结构】二叉树-堆(上)
个人主页~ 二叉树-堆 一、树的概念及结构1、概念2、相关概念3、树的表示4、树的实际应用 二、二叉树的概念和结构1、概念2、特殊二叉树3、二叉树的性质4、二叉树的存储结构(1)顺序存储(2)链式存储 三、二叉树的顺序结构以及实现1、…...

【Spring Boot】在项目中使用Spring AI
Spring AI是Spring框架中用于集成和使用人工智能和机器学习功能的组件。它提供了一种简化的方式来与AI模型进行交互。下面是一个简单的示例,展示了如何在Spring Boot项目中使用Spring AI。 步骤 1: 添加依赖 首先,在pom.xml文件中添加Spring AI的依赖&…...

【java程序设计期末复习】chapter3 运算符、表达式和语句
运算符、表达式和语句 Java提供了丰富的运算符,如算术运算符、关系运算符、逻辑运算符、位运算符等。 Java语言中的绝大多数运算符和C语言相同,基本语句,如条件分支语句、循环语句等也和C语言类似,因此,本章就主要知识…...

【建议收藏】30个较难Python脚本,纯干货分享
本篇较难,建议优先学习上篇 ;20个硬核Python脚本-CSDN博客 接上篇文章,对于Pyhon的学习,上篇学习的结束相信大家对于Pyhon有了一定的理解和经验,学习完上篇文章之后再研究研究剩下的30个脚本你将会有所成就&…...

01-05.Vue自定义过滤器
目录 前言过滤器的概念过滤器的基本使用给过滤器添加多个参数 前言 我们接着上一篇文章01-04.Vue的使用示例:列表功能 来讲。 下一篇文章 02-Vue实例的生命周期函数 过滤器的概念 概念:Vue.js 允许我们自定义过滤器,可被用作一些常见的文本…...

C++系列-static成员
🌈个人主页:羽晨同学 💫个人格言:“成为自己未来的主人~” 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量,用static修饰的成员函数,称之为静态成…...

Git | 创建和管理Pull Request总结
如是我闻: 在使用 GitHub 进行项目协作时,掌握如何创建、更新和合并(squash)pull request 是非常有帮助的。本文将详细介绍这些操作,帮助我们更好地管理项目代码,并解释每个操作的原因和解决的问题。 1. 什…...

电机控制系列模块解析(23)—— 同步机初始位置辨识
一、两个常见问题 为什么感应电机(异步机)不需要初始位置辨识?(因此感应电机转子磁场在定子侧进行励磁,其初始位置可以始终人为定义为0) 为什么同步磁阻电机需要初始位置辨识?(因为…...
【数据库基础-mysql详解之索引的魅力(N叉树)】
索引的魅力目录 🌈索引的概念🌈使用场景🌈索引的使用🌞🌞🌞查看MySQL中的默认索引🌞🌞🌞创建索引🌞🌞🌞删除索引 站在索引背后的那个男…...
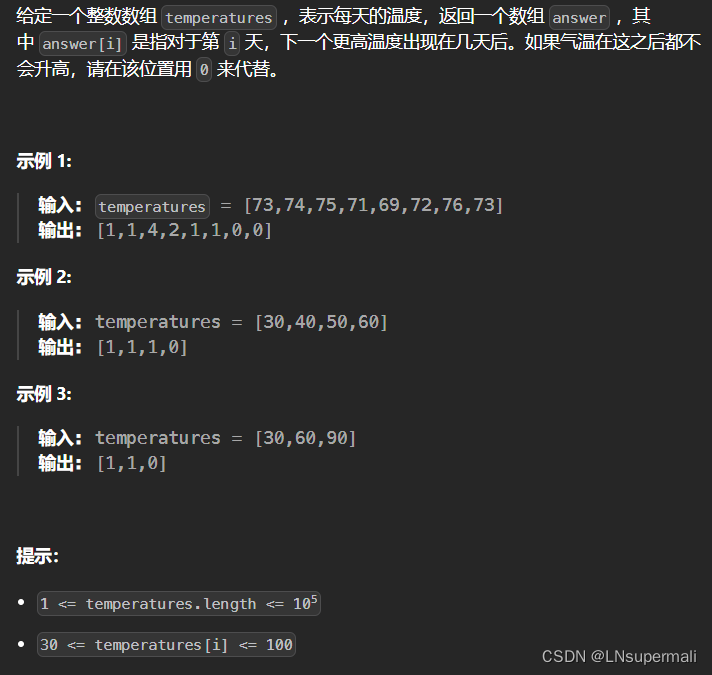
力扣739. 每日温度
Problem: 739. 每日温度 文章目录 题目描述思路复杂度Code 题目描述 思路 若本题目使用暴力法则会超时,故而使用单调栈解决: 1.创建结果数组res,和单调栈stack; 2.循环遍历数组temperatures: 2.1.若当stack不为空同时…...

KDE6桌面于2024年2月发布
原文:KDE MegaRelease 6 - KDE 社区 1. **Plasma 6 桌面环境**:KDE Plasma 是一个现代化、功能丰富的 Linux 操作系统桌面环境,以其时尚设计、可定制界面和广泛的应用程序而闻名。Plasma 6 带来了两项重大技术升级:过渡到最新的应…...

「TypeScript系列」TypeScript 对象及对象的使用场景
文章目录 一、TypeScript 对象1. 对象字面量2. 类实例化3. 使用接口定义对象形状4. 使用类型别名定义对象类型5. 使用工厂函数创建对象 二、TypeScript 对象属性及方法1. 对象属性2. 对象方法3. 访问器和修改器(Getters 和 Setters) 三、TypeScript 对象…...
shell正则匹配~=)
shell从入门到精通(22)shell正则匹配~=
文章目录 1. 基本用法2. 正则表达式捕获组(catch group)3. 匹配结果提取1. 基本用法 在 Shell 脚本中,可以使用正则表达式进行文本匹配和提取。Bash shell 支持使用 [[ … =~ … ]] 结构进行正则表达式匹配,同时还能提取匹配结果。 以下是一个简单的例子,展示了如何在 Bas…...

【Spring】使用Spring常用导入依赖介绍
当使用Spring框架时,以下是常用导入的依赖的详细介绍,按照不同的功能和类别进行分点表示和归纳: 1、核心依赖 Spring Core (spring-core) 功能:提供了Spring框架的基础功能,包括IoC(控制反转)…...

PC端应用订阅SDK接入攻略
本文档介绍了联想应用联运sdk接入操作指南,您可在了解文档内容后,自行接入应用联运sdk。 1. 接入前准备 1. 请先与联想商务达成合作意向。 2. 联系联想运营,提供应用和公司信息,并获取商户id、app id、key(公私钥、…...

WebService的wsdl详解
webservice服务的wsdl内容详解,以及如何根据其内容编写调用代码 wsdl示例 展示一个webservice的wsdl,及调用这个接口的Axis客户端 wsdl This XML file does not appear to have any style information associated with it. The document tree is shown…...
数据分析实战:从0到1完成数据获取分析到可视化
文章目录 1.数据分析基本流程1.1 数据采集1.2 数据提炼1.3 数据探索分析 2.数据获取的方法和工具2.1 数据解锁器2.2 爬虫浏览器2.3 数据洞察市场 3.完整案例分析:从数据采集到数据可视化3.1 直接按需定制数据集获取数据3.2 获取IP代理,利用python爬取数据…...

【Spring】深入理解 Spring 中的 ImportSelector、Aware 和 Processor 接口
前言 Spring 框架提供了一系列接口和机制,为开发者提供了灵活、可扩展的编程模型。其中,ImportSelector、Aware 接口以及 Processor 系列接口是非常重要的扩展点,本文将深入探讨它们的设计目的、使用方法以及示例应用。 一、ImportSelector…...
【C语言】strstr函数的使用和模拟
前言 今天给大家带来一个字符串函数,strstr()的使用介绍和模拟实现。 模拟实现这个函数,可以帮助我们更深刻地理解这个函数的功能和提高解决字符串相关问题的能力,有兴趣的话就请往下看吧。 strstr函数介绍 函数功能: strstr函…...
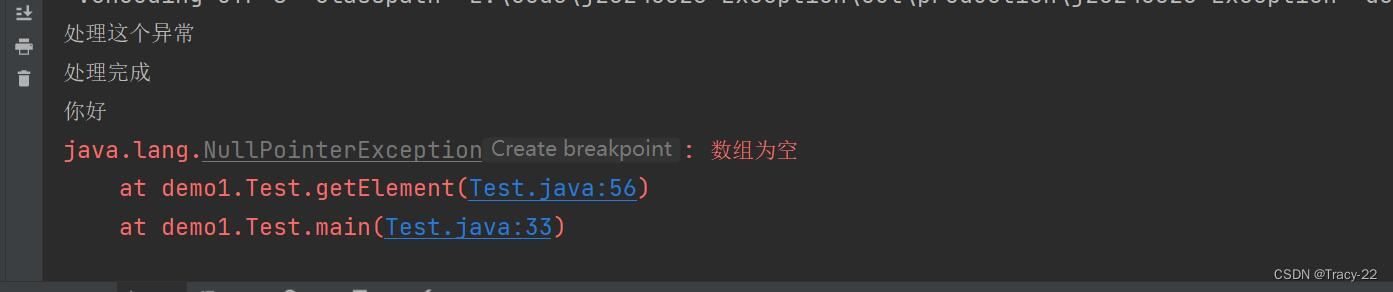
五分钟”手撕“异常
目录 一、什么是异常 二、异常的体系和分类 三、异常的处理 1.抛出异常 2.异常的捕获 异常声明throws: try-catch处理 四、finally finally一定会被执行吗? 五、throw和throws区别 六、异常处理的流程 七、自定义异常 一、什么是异常 顾名…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
