LINGO:存贮问题
存贮模型中的基本概念
模型:

基本要素:
基本费用:
存贮策略:
基本存贮模型
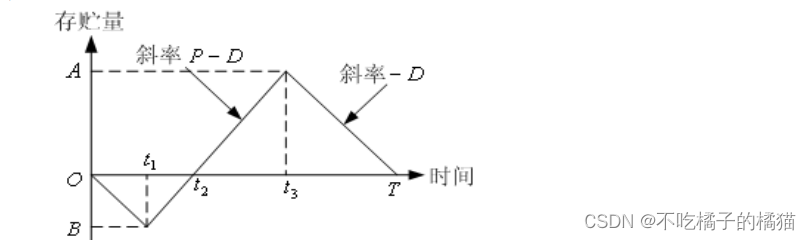
模型一:不允许缺货,补充时间极短(基本的经济订购批量存贮模型)
model:
sets:
times/1 2/:n,Q,C;
endsets
data:
n=57 58;
enddata
C_D=10;
D=100*365;
C_P=0.005*365;
@for(times:n=D/Q;C=0.5*C_P*Q+C_D*D/Q);
end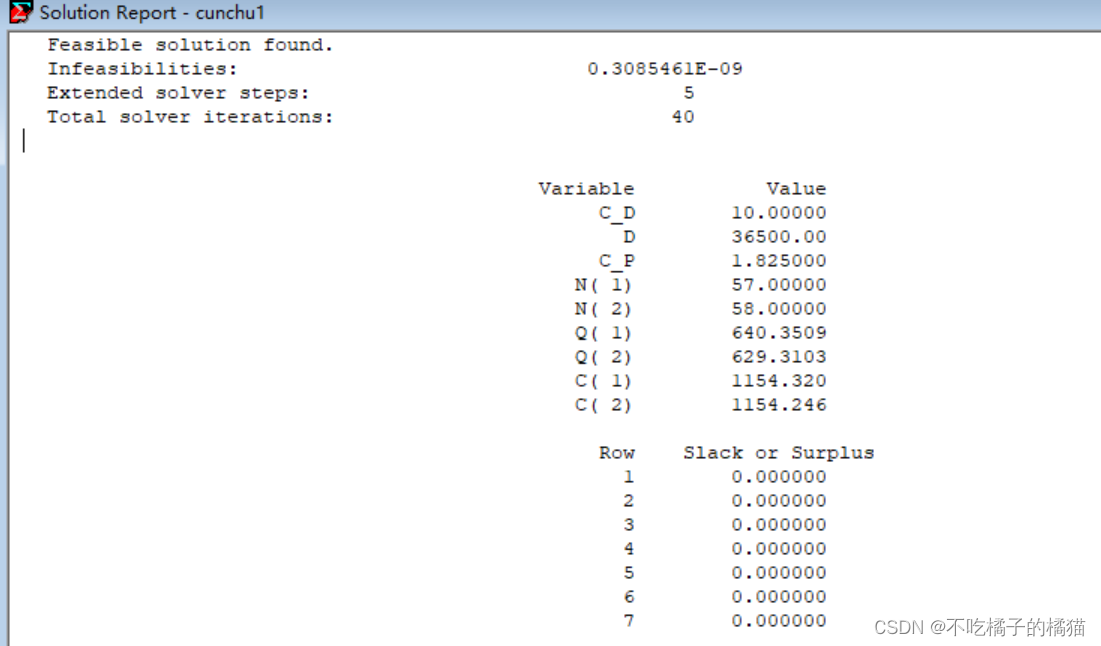
求整数解:
model:
sets:
times/1..100/:C,Q; !100不是必须的,通常取一个适当大的数就可以了;
endsets
C_D=10;
D=100*365;
C_P=0.005*365;
@for(times(i):Q(i)=D/i;C(i)=0.5*C_P*Q+C_D*D/Q);
C_min=@min(times:C);
Q_best=@sum(times(i):Q(i)*(C(i) #eq# C_min));
!(C(i) #eq# C_min)返回的值为0或1;
N_best=D/Q_best;
end
模型二:允许缺货,补充时间较长(经济生产批量存贮模型)
例:有一个生产和销售图书设备的公司,经营一种图书专用设备,基于以往的销售记录和今后市场预测。估计今后一年的需求量为4900个,由于占用资金的利息以及存贮库房和其它人力物力的费用,存贮一个书架一年要花费1000元。这种书架是该公 司自己生产的,每年的生产量9800个,而组织一次生产要花费设备调试等生产准备费500元。如果允许缺货,缺货费为每年每件2000元。该公司为了把成本降到最低,应如何组织生产?要求出其生产、存贮周期,每个周期的最优生产量,以及最少的年总费用。
model:
D=4900;
C_P=1000;
P=9800;
C_D=500;
C_S=2000;
T=(2*C_D*(C_P+C_S)/(D*C_P*C_S*(1-D/P)))^0.5; !单位为年;
TT=T*365; !单位为天;
Q=D*T;
T_S=C_P*TT/(C_P+C_S); !求缺货时间;
T_P=D*TT/P; ! 求生产周期;
C=2*C_D/T; ! 求年总费用;
end模型三:不允许缺货,补充时间较长(基本的经济生产批量存贮模型)

model:
min=0.5*C_P*(Q-S)^2/Q+C_D*D/Q+0.5*C_S*S^2/Q;
n=D/Q;@gin(n);
data:
C_D=12000;
D=96000;
C_P=3.6;
C_S=13.2;
enddata
end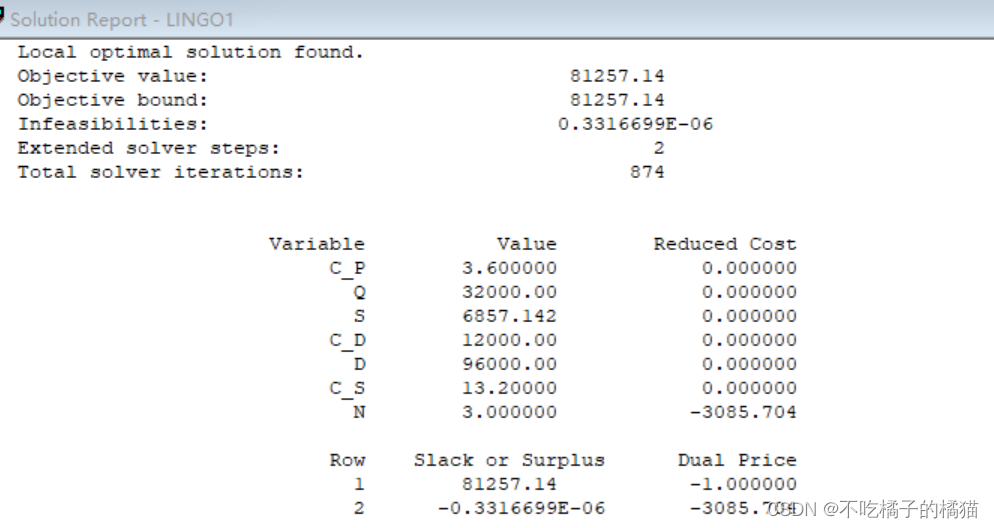
相关文章:

LINGO:存贮问题
存贮模型中的基本概念 模型: 基本要素: (1)需求率:单位时间内对某种物品的需求量,用D表示。 (2)订货批量:一次订货中,包含某种货物的数量,用 Q表…...

《微服务王国的守护者:Spring Cloud Dubbo的奇幻冒险》
5. 经典问题与解决方案 5.3 服务追踪与链路监控 在微服务架构的广袤宇宙中,服务间的调用关系错综复杂,如同一张庞大的星系网络。当一个请求穿越这个星系,经过多个服务节点时,如何追踪它的路径,如何监控整个链路的健康…...
npm 使用)
(九)npm 使用
视频链接:尚硅谷2024最新版微信小程序 文章目录 使用 npm 包自定义构建 npmVant Weapp 组件库的使用Vant Weapp 组件样式覆盖使用 npm 包 目前小程序已经支持使用 npm 安装第三方包,因为 node_modules 目录中的包不会参与小程序项目的编译、上传和打包, 因此在小程序项目中要…...
Thinkphp5内核宠物领养平台H5源码
源码介绍 Thinkphp5内核流浪猫流浪狗宠物领养平台H5源码 可封装APP,适合做猫狗宠物类的发信息发布,当然懂的修改一下,做其他信息发布也是可以的。 源码预览 源码下载 https://download.csdn.net/download/huayula/89361685...
一、Elasticsearch介绍与部署
目录 一、什么是Elasticsearch 二、安装Elasticsearch 三、配置es 四、启动es 1、下载安装elasticsearch的插件head 2、在浏览器,加载扩展程序 3、运行扩展程序 4、输入es地址就可以了 五、Elasticsearch 创建、查看、删除索引、创建、查看、修改、删除文档…...
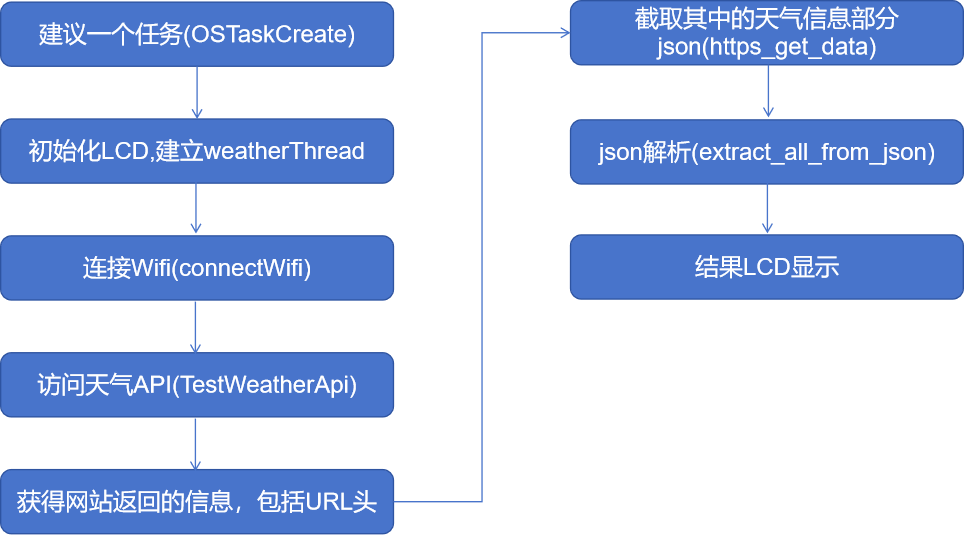
NL6621 实现获取天气情况
一、主要完成的工作 1、建立TASK INT32 main(VOID) {/* system Init */SystemInit();OSTaskCreate(TestAppMain, NULL, &sAppStartTaskStack[NST_APP_START_TASK_STK_SIZE -1], NST_APP_TASK_START_PRIO); OSStart();return 1; } 2、application test task VOID TestAp…...

SpringCloud配置文件bootrap
解决方案: 情况一、SpringBoot 版本 小于 2.4.0 版本,添加以下依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-context</artifactId> </dependency> 情况二、SpringBoot…...

经典面试题:进程、线程、协程开销问题,为什么进程切换的开销比线程的大?
上下文切换的过程? 上下文切换是操作系统在将CPU从一个进程切换到另一个进程时所执行的过程。它涉及保存当前执行进程的状态并加载下一个将要执行的进程的状态。下面是上下文切换的详细过程: 保存当前进程的上下文: 当操作系统决定切换到另…...

鸿蒙 DevEco Studio 3.1 Release 下载sdk报错的解决办法
鸿蒙 解决下载SDK报错的解决方法 最近在学习鸿蒙开发,以后也会记录一些关于鸿蒙相关的问题和解决方法,希望能帮助到大家。 总的来说一般有下面这样的报错 报错一: Components to install: - ArkTS 3.2.12.5 - System-image-phone 3.1.0.3…...

QGIS开发笔记(二):Windows安装版二次开发环境搭建(上):安装OSGeo4W运行依赖其Qt的基础环境Demo
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/139136356 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

设计一套Kafka到RocketMQ的双写+双读技术方案,实现无缝迁移!
设计一套Kafka到RocketMQ的双写双读技术方案,实现无缝迁移! 1、背景2、方案3、具体逻辑 1、背景 假设你们公司本来线上的MQ用的主要是Kafka,现在要从Kafka迁移到RocketMQ去,那么这个迁移的过程应该怎么做呢?应该采用什…...
)
Mysql下Limit注入方法(此方法仅适用于5.0.0<mysql<5.6.6的版本)
SQL语句类似下面这样:(此方法仅适用于5.0.0<mysql<5.6.6的版本) SELECT field FROM table WHERE id > 0 ORDER BY id LIMIT (注入点) 问题的关键在于,语句中有 order by 关键字,mysql…...

Makefile学习笔记15|u-boot顶层Makefile01
Makefile学习笔记15|u-boot顶层Makefile01 希望看到这篇文章的朋友能在评论区留下宝贵的建议来让我们共同成长,谢谢。 这里是目录 版本号信息 # SPDX-License-Identifier: GPL-2.0VERSION 2024 PATCHLEVEL 01 SUBLEVEL EXTRAVERSION -rc4 NAME 这里定义了u-bo…...

C++笔记之Unix时间戳、UTC、TSN、系统时间戳、时区转换、local时间笔记
C++笔记之Unix时间戳、UTC、TSN、系统时间戳、时区转换、local时间笔记 ——2024-05-26 夜 code review! 参考博文 C++笔记之获取当前本地时间以及utc时间...

leetcode338-Counting Bits
题目 给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 示例 1: 输入:n 2 输出:[0,1,1] 解释: 0 --> 0 1 --&…...

sql server怎么存储图片
sql server怎么存储图片 在SQL Server中,可以使用VARBINARY数据类型来存储图片。以下是一个简单的例子,展示了如何将图片存储到数据库中,并从数据库中检索出来。 首先,创建一个表来存储图片数据: CREATE TABLE Image…...

大模型提示词Prompt学习
引言 关于chatGPT的Prompt Engineer,大家肯定耳朵都听起茧了。但是它的来由?,怎么能用好?很多人可能并不觉得并不是一个问题,或者说认定是一个很快会过时的概念。但其实也不能说得非常清楚(因为觉得没必要深…...

蓝桥杯python组备赛指南
文章目录 前言刷题网站idle操作常用标准库mathdatetime 常见Q&A 前言 最近结束了比赛,我对比赛的过程进行了详细的复盘,并计划撰写一篇文章。这篇文章旨在为准备参加蓝桥杯的学弟学妹们提供帮助,我希望我的文章和笔记能对你们有所裨益。…...
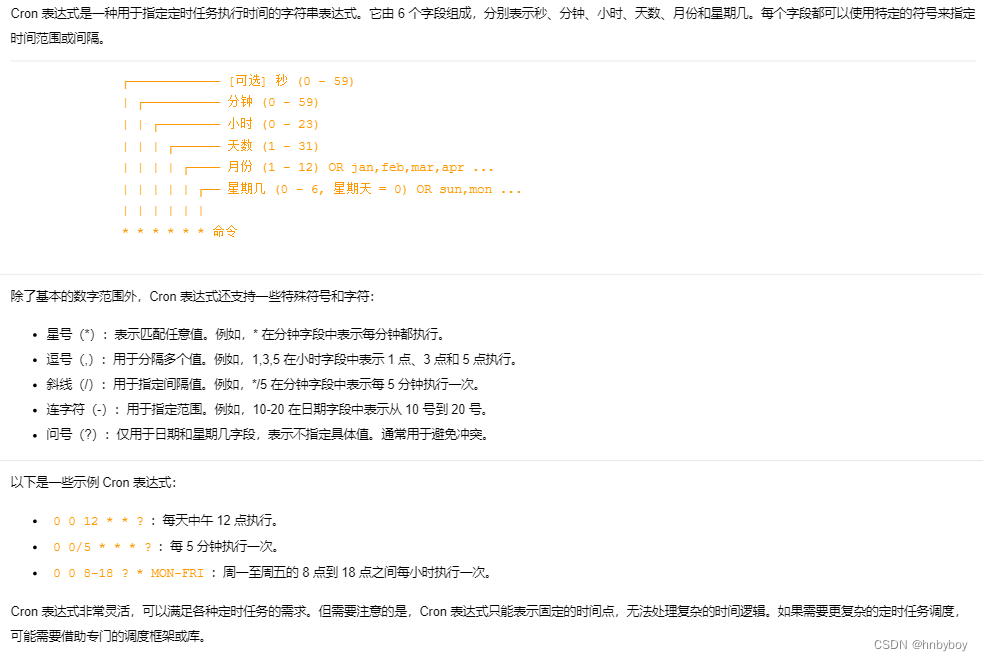
架构师系列-定时任务解决方案
定时任务概述 在很多应用中我们都是需要执行一些定时任务的,比如定时发送短信,定时统计数据,在实际使用中我们使用什么定时任务框架来实现我们的业务,定时任务使用中会遇到哪些坑,如何最大化的提高定时任务的性能。 我…...

新计划,不断变更!做自己,接受不美好!猪肝移植——早读(逆天打工人爬取热门微信文章解读)
时间不等人 引言Python 代码第一篇 做自己,没有很好也没关系第二篇结尾 引言 新计划: 早上一次性发几个视频不现实 所以更改一下 待后面有比较稳定的框架再优化 每天早上更新 早到8点 晚到10点 你刚刚好上班或者上课 然后偷瞄的看两眼 学习一下 补充知…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...