java list<AnalystEducationDO> 转成List<AnalystEducationRespVO>两个对象的属性一样
如果AnalystEducationDO和AnalystEducationRespVO两个类的属性完全相同,且遵循Java Bean的命名规范(即具有相应的getter和setter方法),你可以利用一些库来简化转换过程,比如Apache BeanUtils或Spring Framework的BeanUtils。以下是使用Spring Framework的BeanUtils进行转换的例子:
首先,确保你的项目中已经引入了Spring Framework的依赖,特别是spring-beans模块。
然后,可以编写如下的转换方法:
import org.springframework.beans.BeanUtils;
import java.util.ArrayList;
import java.util.List;public class ConversionExample {public List<AnalystEducationRespVO> convertToRespVOList(List<AnalystEducationDO> doList) {List<AnalystEducationRespVO> voList = new ArrayList<>(doList.size());for (AnalystEducationDO educationDO : doList) {AnalystEducationRespVO respVO = new AnalystEducationRespVO();BeanUtils.copyProperties(educationDO, respVO);voList.add(respVO);}return voList;}
}
这段代码中,BeanUtils.copyProperties()方法会将源对象(AnalystEducationDO实例)的所有属性复制到目标对象(AnalystEducationRespVO实例)中,前提是这两个类有相同的属性名和类型,并且遵循Java Bean规范。
这种方法简化了转换逻辑,特别是当对象有很多属性时,避免了手动逐个设置属性的繁琐。但请注意,这种方式也可能会导致性能开销,尤其是在处理大量对象或复杂对象结构时。对于简单且属性一致的情况,这是一个非常直接和便捷的解决方案。
相关文章:

java list<AnalystEducationDO> 转成List<AnalystEducationRespVO>两个对象的属性一样
如果AnalystEducationDO和AnalystEducationRespVO两个类的属性完全相同,且遵循Java Bean的命名规范(即具有相应的getter和setter方法),你可以利用一些库来简化转换过程,比如Apache BeanUtils或Spring Framework的BeanU…...
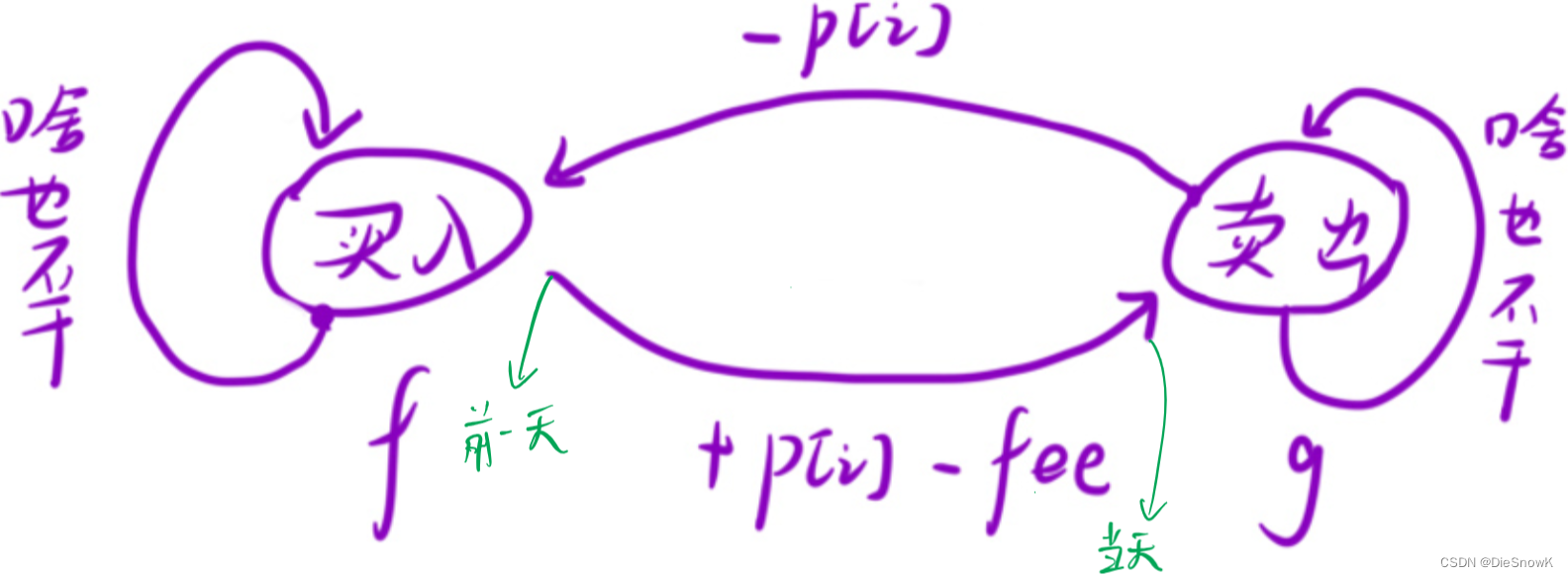
[Algorihm][简单多状态DP问题][买卖股票的最佳时机含冷冻期][买卖股票的最佳时机含手续费]详细讲解
目录 1.买卖股票的最佳时机含冷冻期1.题目链接买卖股票的最佳时机含冷冻期2.算法原理详解3.代码实现 2.买卖股票的最佳时机含手续费1.题目链接2.算法原理详解3.代码实现 1.买卖股票的最佳时机含冷冻期 1.题目链接 买卖股票的最佳时机含冷冻期 2.算法原理详解 思路ÿ…...
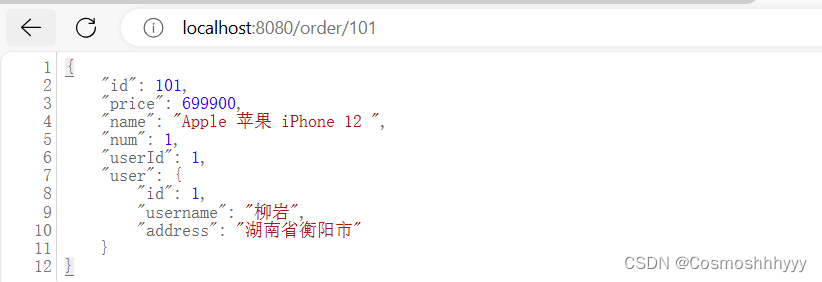
微服务:利用RestTemplate实现远程调用
打算系统学习一下微服务知识,从今天开始记录。 远程调用 调用order接口,查询。 由于实现还未封装用户信息,所以为null。 下面我们来使用远程调用用户服务的接口,然后封装一下用户信息返回即可。 流程图 配置类中注入RestTe…...
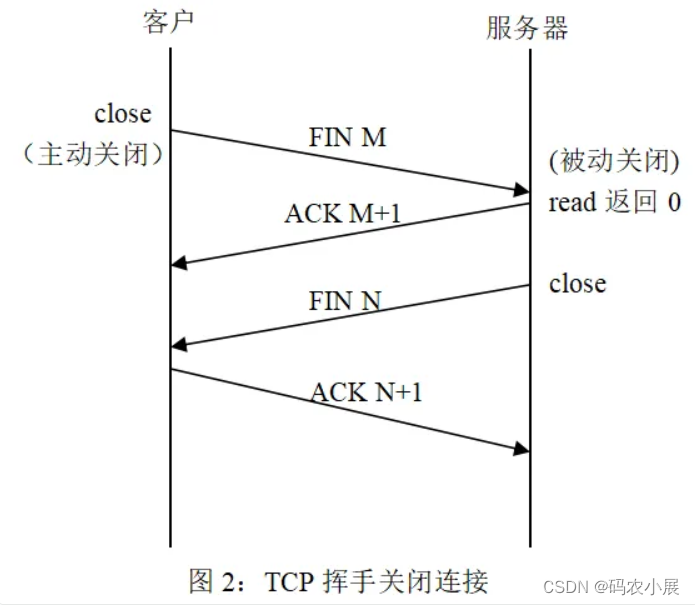
【Linux】TCP的三次握手和四次挥手
三次握手 在TCP/IP协议中,TCP协议提供可靠的连接服务,采用三次握手建立一个连接。注意!三次握手只是用来建立连接用的,和TCP可靠稳定没有关系,TCP的可靠是通过重传和检错等机制实现的。 默认创建一个socket后ÿ…...
爬山算法全解析:掌握优化技巧,攀登技术高峰!
一、引言 爬山算法是一种局部搜索算法,它基于当前解的邻域中进行搜索,通过比较当前解与邻域解的优劣来更新当前解,从而逐步逼近最优解。本文将对爬山算法进行详细的介绍。 二、爬山算法简介 爬山算法是一种基于贪心策略的优化算法ÿ…...
使用 Ollama框架 下载和使用 Llama3 AI大模型的完整指南
🏡作者主页:点击! 🤖AI大模型部署与应用专栏:点击! ⏰️创作时间:2024年5月24日20点59分 🀄️文章质量:96分 目录 💥Ollama介绍 主要特点 主要优点 应…...
最新流媒体在线音乐系统网站源码| 音乐社区 | 多语言 | 开心版
最新流媒体在线音乐系统网站源码 源码免费下载地址抄笔记 (chaobiji.cn)...
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力?
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力? 《中国改革报》是国家发展和改革委员会主管的全国性综合类报纸。它在经济领域和改革发展方面具有重要的影响力,是传递国家政策、反映改革动态的重要平台。该报对于推动中国的经济改…...
乡村振兴的乡村公共服务提升:提升乡村公共服务水平,满足农民多样化需求,构建幸福美好的美丽乡村
目录 一、引言 二、乡村公共服务提升的必要性 (一)满足农民多样化需求 (二)促进乡村经济发展 (三)构建幸福美好的美丽乡村 三、乡村公共服务面临的挑战 (一)基础设施薄弱 &a…...

【在 Windows 上使用 ADB 安装 Android 设备上的 atx-agent】
在进行 Android 应用的 UI 自动化测试时,通常需要在设备上安装一些辅助工具。其中一个常用的工具是 atx-agent,它可以帮助我们在 Android 设备上进行 UI 自动化操作。本文将介绍如何在 Windows 环境下使用 ADB 安装 Android 设备上的 atx-agent。 1. 下…...

iptables 防火墙
linux防火墙基础 iptables的表,链结构 数据包控制的匹配流程 编写防火墙规则 基本语法,控制类型 添加,查看,删除规则 规则的匹配条件 iptables组件 netfilter :属于内核态的功能体系,是一个内核模块…...
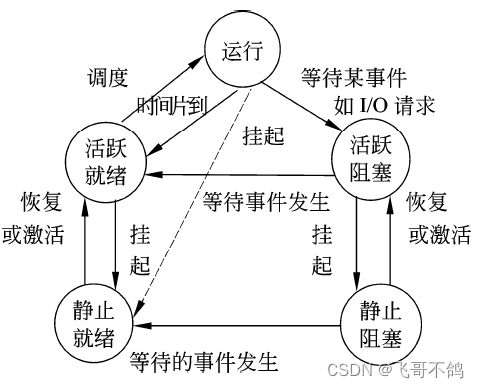
软件设计师笔记1
分享一下学习软考时做的笔记,笔者太懒了,后续篇章都没咋记录,现在放出来水几篇文章 另外,本章内容都是结合教材,B站课堂记录。下一篇软考笔记知识点来自真题 软考笔记 第一章 1. 计算机的组成 1. 控制器 控制器由…...

springboot集成mybatis 单元测试
1、依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0…...

ecc dsa rsa des
ECC(椭圆曲线密码学)、DSA(数字签名算法)、RSA(一种公钥加密技术)和DES(数据加密标准)都是密码学领域中重要的加密和安全技术。下面是对这四种技术的简要介绍: 椭圆曲线密…...
)
Gitee的原理及应用详解(三)
本系列文章简介: Gitee是一款开源的代码托管平台,是国内最大的代码托管平台之一。它基于Git版本控制系统,提供了代码托管、项目管理、协作开发、代码审查等功能,方便团队协作和项目管理。Gitee的出现,在国内的开发者社…...

Mia for Gmail for Mac:Mac用户的邮件管理首选
对于追求高效工作的Mac用户来说,Mia for Gmail for Mac无疑是邮件管理的首选工具。它以其卓越的性能和丰富的功能,为用户带来了前所未有的高效邮件管理体验。 Mia for Gmail for Mac不仅支持多帐号登录和标签选择功能,还提供了邮件分类、垃圾…...
如何在忘记密码的情况下解锁 iPhone? 6 种方法分享
您是否因为没有密码而无法解锁您的 iPhone? 别担心,这种情况比你想象的更常见!忘记密码是 iPhone 用户面临的最常见问题之一,而且可能非常令人沮丧 - 但不要绝望。 在这篇文章中,我们将与您分享绕过 iPhone 屏幕密码…...

国产操作系统上使用rsync恢复用户数据 _ 统信 _ 麒麟 _ 中科方德
原文链接:国产操作系统上使用rsync恢复用户数据 | 统信 | 麒麟 | 中科方德 Hello,大家好啊!今天给大家带来一篇关于在国产操作系统上使用rsync备份并还原用户数据的文章。rsync是一款功能强大的文件同步和备份工具,广泛用于Linux系…...

Elastic Cloud 将 Elasticsearch 向量数据库优化配置文件添加到 Microsoft Azure
作者:来自 Elastic Serena Chou, Jeff Vestal, Yuvraj Gupta 今天,我们很高兴地宣布,我们的 Elastic Cloud Vector Search 优化硬件配置文件现已可供 Elastic Cloud on Microsoft Azure 用户使用。 此硬件配置文件针对使用 Elasticsearch 作…...
Mongodb 可视化工具Robot 3t安装【windows环境下】
下载应用 打开连接点我 选择windows版本并点击下载 下载完毕,双击并傻瓜安装 连接数据库 点击图标, 点击create创建连接 填写host和port 如果有用户名密码的,在authentication里填写 5. save 并连接即可使用!...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
