685. 冗余连接 II
685. 冗余连接 II
问题描述
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:
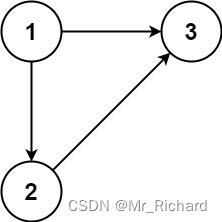
输入:edges = [[1,2],[1,3],[2,3]]
输出:[2,3]
示例 2:

输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出:[4,1]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ui, vi <= n
解题思路与代码实现
总共有两种情况:
- 存在入度为2的点,不满足有向树的要求,需要删除一条边使该节点入度为1。如果删了一条,判断这个图是一个树,那么这条边就是答案,同时注意要从后向前遍历,因为如果两条边删哪一条都可以成为树,就删最后那一条。
- 不存在入度为2的点,说明此时存在有向环,需要删除一条边破坏有向环,此时就变成了并查集模板题。
class Solution {private static final int N = 1010; // 如题:二维数组大小的在3到1000范围内private int[] father;public Solution() {father = new int[N];// 并查集初始化for (int i = 0; i < N; ++i) {father[i] = i;}}// 并查集里寻根的过程private int find(int u) {if (u == father[u]) {return u;}// 路径压缩father[u] = find(father[u]);return father[u];}// 将v->u 这条边加入并查集private void join(int u, int v) {u = find(u);v = find(v);if (u == v)return;father[v] = u;}// 判断 u 和 v是否找到同一个根private Boolean same(int u, int v) {u = find(u);v = find(v);return u == v;}/*** 初始化并查集*/private void initFather() {// 并查集初始化for (int i = 0; i < N; ++i) {father[i] = i;}}/*** 在有向图里找到删除的那条边,使其变成树* * @param edges* @return 要删除的边*/private int[] getRemoveEdge(int[][] edges) {initFather();for (int i = 0; i < edges.length; i++) {if (same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边return edges[i];}join(edges[i][0], edges[i][1]);}return null;}/*** 删一条边之后判断是不是树* 判断题目中的有向树是否存在环* @param edges* @param deleteEdge 要删除的边* @return true: 是树, false: 不是树*/private Boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge) {initFather();for (int i = 0; i < edges.length; i++) {if (i == deleteEdge)continue;if (same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树return false;}join(edges[i][0], edges[i][1]);}return true;}public int[] findRedundantDirectedConnection(int[][] edges) {int[] inDegree = new int[N];// 根据edges数组计算每个点入度for (int i = 0; i < edges.length; i++) {// 入度inDegree[edges[i][1]] += 1;}// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案ArrayList<Integer> twoDegree = new ArrayList<Integer>();for (int i = edges.length - 1; i >= 0; i--) {if (inDegree[edges[i][1]] == 2) {twoDegree.add(i);}}// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树if (!twoDegree.isEmpty()) {if (isTreeAfterRemoveEdge(edges, twoDegree.get(0))) {return edges[twoDegree.get(0)];}return edges[twoDegree.get(1)];}// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了return getRemoveEdge(edges);}
}
踩坑点
无
相关文章:

685. 冗余连接 II
685. 冗余连接 II 问题描述 在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。 输入一个有向图,该…...

自养号测评是什么?亚马逊、沃尔玛、Target卖家如何建立自己的护城河?
近期有跨境卖家咨询我自养买家账号测评的事情,他们还是有不了解自养号测评的,所以珑哥觉得有必要再讲一下卖家测评的一些事情,之前文章也说过。这可能是跨境卖家运营的一个趋势。今天珑哥着重来介绍一下自养号测评 一、什么叫做自养号测评&a…...

计算机毕业设计 | SpringBoot招投标 任务发布网站(附源码)
1,绪论 在市场范围内,任务发布网站很受欢迎,有很多开发者以及其他领域的牛人,更倾向于选择工作时间、工作场景更自由的零工市场寻求零散单子来补贴家用。 如今市场上,任务发布网站鱼龙混杂,用户需要找一个…...

element el-table表格表头某一列表头文字或者背景修改颜色
效果如下 整体代码 ,具体方法在最下面! <el-table v-loading"listLoading" :data"sendReceivList" element-loading-text"Loading" border fit ref"tableList" :header-cell-class-name"addClass&quo…...

移动云:连接未来的智慧之旅
随着数字化转型的加速,云服务在各行各业中的应用越来越广泛。移动云不仅提供了灵活的计算和存储资源,还通过创新的技术手段,为企业和开发者解决了许多实际问题。在这个变革的大背景下,移动云服务作为中国移动倾力打造的云业务品牌…...

如何确保大模型 RAG 生成的信息是基于可靠的数据源?
在不断发展的人工智能 (AI) 领域中,检索增强生成 (RAG) 已成为一种强大的技术。 RAG 弥合了大型语言模型 (LLM) 与外部知识源之间的差距,使 AI 系统能够提供更全面和信息丰富的响应。然而,一个关键因素有时会缺失——透明性。 我们如何能够…...
 + Supervisor 实现多进程redis消息队列)
Laravel(Lumen8) + Supervisor 实现多进程redis消息队列
相关文章:Supervisor守护进程工具安装与使用 1、通用消息队列 /App/Job/CommonJob.php: <?phpnamespace App\Jobs; use Illuminate\Support\Facades\Log; use Illuminate\Support\Str;class CommonJob extends Job {public $timeout; //超时时间protected $data; //队列…...

深度学习复盘与小实现
文章目录 一、查漏补缺复盘1、python中zip()用法2、Tensor和tensor的区别3、计算图中的迭代取数4、nn.Modlue及nn.Linear 源码理解5、知识杂项思考列表6、KL散度初步理解 二、处理多维特征的输入1、逻辑回归模型流程2、Mini-Batch (N samples) 三、加载数据集1、Python 魔法方法…...
)
算法刷题笔记 高精度加法(C++实现)
文章目录 题目描述题目思路和代码 题目描述 给定两个正整数(不含前导0),计算它们的和。 输入格式 共两行,每行包含一个整数。 输出格式 共一行,包含所求的和。 题目思路和代码 基本思路:模拟竖式计算…...

php祛除mqtt 返回数据中包含的特殊字符
function cleanseMessage($message) {// 定义特殊字符的正则表达式$pattern /[[:^print:]]/;// 使用正则表达式替换特殊字符为空字符串$cleanedMessage preg_replace($pattern, , $message);return $cleanedMessage; }// 假设接收到的MQTT消息是: $rawMessage &q…...

2024,java开发,已经炸了吗?
网友: 炸的透透的了,坐标南京。 一月底,一个好哥们,双休朝九晚六不加班18K,被裁。 入职不到两年,算是工资和年终奖才赔了6.5W左右。 上周五新公司入职,周六开始加班。现在每周134加班到晚上八…...

c++基础篇
一、命名空间: 1.1命名空间存在的意义: 1.1要知道c是对c语言缺点的完善,而在c语言中我们是知道,定义变量、函数名或者全域名是不能相同的,否则会产生冲突,但要知道这都是大量存在的,就像一个名…...

卫浴行业All in 智能化,国货品牌拿到了先手棋
想要了解一个行业的趋势和风向,展会可以说是最佳的窗口。 比如半个月前在上海举办的第28届中国国际厨房、卫浴设施展览会上,1500多家国内外企业同台竞技,给出了各自的解决方案,其中“智能化”已成为出镜率最高的词汇。 走在数智…...

分享10个国内可以使用的GPT中文网站
在今天的人工智能领域,基于对话的语言模型已成为研究的热点,尤其是像 ChatGPT 这样因其出色的语言理解与对话交互能力而广受关注的模型。本文将介绍10个国内可以直接使用GPT的网站,旨在为大家在选择和使用这些优秀的AI工具时提供有价值的参考…...

golang实现mediasoup的tcp服务及channel通道
tcp模块 定义相关类 Client:表示客户端连接,包含网络连接conn、指向服务器的指针Server和Channel指针c。server:表示TCP服务器,包含服务器地址address、TLS配置config以及三个回调函数: onNewClientCallback…...

Spring:IoC容器(基于注解管理bean)
1. HelloWorld * 引入依赖* 开启组件扫描* 使用注解定义 Bean* 依赖注入 2.开启组件扫描 <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/20…...

如何解决Redis缓存雪崩问题?
解决Redis缓存雪崩问题,可以从多个方面入手来确保系统在高并发和缓存失效时能够保持稳定运行。以下是一些具体的解决策略: 合理设置缓存过期时间: 避免大量缓存设置相同的过期时间,这样会导致在某一时刻缓存同时失效,…...

vue3的组件通信v-model使用
一、组件通信 1.props 》 父向子传值 props 主要用于父组件向子组件通信。再父组件中通过使用:msgmsg绑定需要传给子组件的属性值,然后再在子组件中用props接收该属性值 方法一 普通方式:// 父组件 传值<child :msg1"msg1" :list"list">…...

从关键新闻和最新技术看AI行业发展(2024.5.6-5.19第二十三期) |【WeThinkIn老实人报】
写在前面 【WeThinkIn老实人报】旨在整理&挖掘AI行业的关键新闻和最新技术,同时Rocky会对这些关键信息进行解读,力求让读者们能从容跟随AI科技潮流。也欢迎大家提出宝贵的优化建议,一起交流学习💪 欢迎大家关注Rocky的公众号&…...
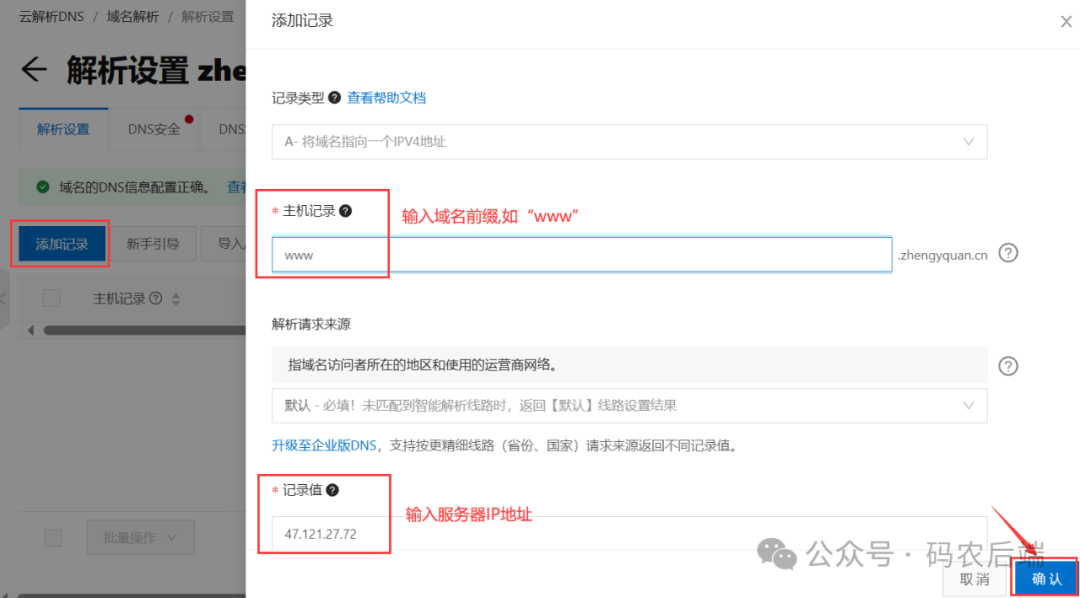
一文带你学会如何部署个人博客到云服务器,并进行域名备案与解析!
哈喽,大家好呀!这里是码农后端。之前我给大家介绍了如何快速注册一个自己的域名,并创建一台自己的阿里云ECS云服务器。本篇将介绍如何将个人博客部署到云服务器,并进行域名备案与解析。 1、域名备案 注册了域名并购买了云服务器之…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
