当前位置： 首页 > news >正文

Sylvester矩阵、子结式、辗转相除法的三者关系(第二部分)

news 2026/2/11 5:50:04

【三者的关系】

首先，辗转相除法可以通过Sylvester矩阵进行，过程如下（以 m = 8 、 l = 7 m = 8、l = 7 m=8、l=7为例子）。

首先调整矩阵中 a a a系数到最后面几行，如下所示：

S = ( a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) ∼ S ′ = ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) S = \begin{pmatrix} a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} \\ b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \end{pmatrix}\sim S^{'} = \begin{pmatrix} b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \\ a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} \end{pmatrix} S= ​a8​000000b7​0000000​a7​a8​00000b6​b7​000000​a6​a7​a8​0000b5​b6​b7​00000​a5​a6​a7​a8​000b4​b5​b6​b7​0000​a4​a5​a6​a7​a8​00b3​b4​b5​b6​b7​000​a3​a4​a5​a6​a7​a8​0b2​b3​b4​b5​b6​b7​00​a2​a3​a4​a5​a6​a7​a8​b1​b2​b3​b4​b5​b6​b7​0​a1​a2​a3​a4​a5​a6​a7​b0​b1​b2​b3​b4​b5​b6​b7​​a0​a1​a2​a3​a4​a5​a6​0b0​b1​b2​b3​b4​b5​b6​​0a0​a1​a2​a3​a4​a5​00b0​b1​b2​b3​b4​b5​​00a0​a1​a2​a3​a4​000b0​b1​b2​b3​b4​​000a0​a1​a2​a3​0000b0​b1​b2​b3​​0000a0​a1​a2​00000b0​b1​b2​​00000a0​a1​000000b0​b1​​000000a0​0000000b0​​ ​∼S′= ​b7​0000000a8​000000​b6​b7​000000a7​a8​00000​b5​b6​b7​00000a6​a7​a8​0000​b4​b5​b6​b7​0000a5​a6​a7​a8​000​b3​b4​b5​b6​b7​000a4​a5​a6​a7​a8​00​b2​b3​b4​b5​b6​b7​00a3​a4​a5​a6​a7​a8​0​b1​b2​b3​b4​b5​b6​b7​0a2​a3​a4​a5​a6​a7​a8​​b0​b1​b2​b3​b4​b5​b6​b7​a1​a2​a3​a4​a5​a6​a7​​0b0​b1​b2​b3​b4​b5​b6​a0​a1​a2​a3​a4​a5​a6​​00b0​b1​b2​b3​b4​b5​0a0​a1​a2​a3​a4​a5​​000b0​b1​b2​b3​b4​00a0​a1​a2​a3​a4​​0000b0​b1​b2​b3​000a0​a1​a2​a3​​00000b0​b1​b2​0000a0​a1​a2​​000000b0​b1​00000a0​a1​​0000000b0​000000a0​​ ​

1.执行辗转相除法第一步

F 8 = Q 8 , 7 × F 7 + F 6 deg ⁡ ( F 8 ) = 8 deg ⁡ ( F 7 ) = 7 deg ⁡ ( F 6 ) = 6 F_{8} = Q_{8,7} \times F_{7} + F_{6}\ \ \ \ \ \ \ \ \ \ \deg\left( F_{8} \right) = 8\ \ \ \ \ \ \deg\left( F_{7} \right) = 7\ \ \ \ \ \ \deg\left( F_{6} \right) = 6 F8​=Q8,7​×F7​+F6​          deg(F8​)=8      deg(F7​)=7      deg(F6​)=6

( − 1 ) 8 × 7 ∣ S ∣ = F 7 F 7 F 7 F 7 F 7 F 7 F 7 F 7 F 8 F 8 F 8 F 8 F 8 F 8 F 8 ∣ b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 0 0 0 0 0 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ∣ = F 7 F 7 F 7 F 7 F 7 F 7 F 7 F 7 F 6 F 6 F 6 F 6 F 6 F 6 F 6 ∣ b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 0 0 0 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 0 0 0 0 0 0 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 ∣ ( - 1)^{8 \times 7}|S| = \begin{matrix} \begin{matrix} F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{8} \\ F_{8} \\ F_{8} \\ F_{8} \\ F_{8} \\ F_{8} \\ F_{8} \end{matrix} & \left| \begin{matrix} b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \\ a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} \end{matrix} \right| \end{matrix} = \begin{matrix} \begin{matrix} F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{7} \\ F_{6} \\ F_{6} \\ F_{6} \\ F_{6} \\ F_{6} \\ F_{6} \\ F_{6} \end{matrix} & \left| \begin{matrix} b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \\ 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} \end{matrix} \right| \end{matrix} (−1)8×7∣S∣=F7​F7​F7​F7​F7​F7​F7​F7​F8​F8​F8​F8​F8​F8​F8​​​ ​b7​0000000a8​000000​b6​b7​000000a7​a8​00000​b5​b6​b7​00000a6​a7​a8​0000​b4​b5​b6​b7​0000a5​a6​a7​a8​000​b3​b4​b5​b6​b7​000a4​a5​a6​a7​a8​00​b2​b3​b4​b5​b6​b7​00a3​a4​a5​a6​a7​a8​0​b1​b2​b3​b4​b5​b6​b7​0a2​a3​a4​a5​a6​a7​a8​​b0​b1​b2​b3​b4​b5​b6​b7​a1​a2​a3​a4​a5​a6​a7​​0b0​b1​b2​b3​b4​b5​b6​a0​a1​a2​a3​a4​a5​a6​​00b0​b1​b2​b3​b4​b5​0a0​a1​a2​a3​a4​a5​​000b0​b1​b2​b3​b4​00a0​a1​a2​a3​a4​​0000b0​b1​b2​b3​000a0​a1​a2​a3​​00000b0​b1​b2​0000a0​a1​a2​​000000b0​b1​00000a0​a1​​0000000b0​000000a0​​ ​​=F7​F7​F7​F7​F7​F7​F7​F7​F6​F6​F6​F6​F6​F6​F6​​​ ​b7​00000000000000​b6​b7​0000000000000​b5​b6​b7​00000c6​000000​b4​b5​b6​b7​0000c5​c6​00000​b3​b4​b5​b6​b7​000c4​c5​c6​0000​b2​b3​b4​b5​b6​b7​00c3​c4​c5​c6​000​b1​b2​b3​b4​b5​b6​b7​0c2​c3​c4​c5​c6​00​b0​b1​b2​b3​b4​b5​b6​b7​c1​c2​c3​c4​c5​c6​0​0b0​b1​b2​b3​b4​b5​b6​c0​c1​c2​c3​c4​c5​c6​​00b0​b1​b2​b3​b4​b5​0c0​c1​c2​c3​c4​c5​​000b0​b1​b2​b3​b4​00c0​c1​c2​c3​c4​​0000b0​b1​b2​b3​000c0​c1​c2​c3​​00000b0​b1​b2​0000c0​c1​c2​​000000b0​b1​00000c0​c1​​0000000b0​000000c0​​ ​​

对应子结式 S 6 S_{6} S6​：

S 6 = ( − 1 ) 2 × 1 d e t p o l ( F 7 F 7 F 8 ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) ) = ( − 1 ) 2 × 1 d e t p o l ( F 7 F 7 F 6 ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 0 c 6 c 5 c 4 c 3 c 2 c 1 c 0 ) ) S_{6} = ( - 1)^{2 \times 1}detpol\begin{pmatrix} \begin{matrix} F_{7} \\ F_{7} \\ F_{8} \end{matrix} & \begin{pmatrix} b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \\ a_{8} & a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & a_{0} \end{pmatrix} \end{pmatrix} = ( - 1)^{2 \times 1}detpol\begin{pmatrix} \begin{matrix} F_{7} \\ F_{7} \\ F_{6} \end{matrix} & \begin{pmatrix} b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} & 0 \\ 0 & b_{7} & b_{6} & b_{5} & b_{4} & b_{3} & b_{2} & b_{1} & b_{0} \\ 0 & 0 & c_{6} & c_{5} & c_{4} & c_{3} & c_{2} & c_{1} & c_{0} \end{pmatrix} \end{pmatrix} S6​=(−1)2×1detpol ​F7​F7​F8​​​ ​b7​0a8​​b6​b7​a7​​b5​b6​a6​​b4​b5​a5​​b3​b4​a4​​b2​b3​a3​​b1​b2​a2​​b0​b1​a1​​0b0​a0​​ ​​ ​=(−1)2×1detpol ​F7​F7​F6​​​ ​b7​00​b6​b7​0​b5​b6​c6​​b4​b5​c5​​b3​b4​c4​​b2​b3​c3​​b1​b2​c2​​b0​b1​c1​​0b0​c0​​ ​​ ​

相关文章：

Sylvester矩阵、子结式、辗转相除法的三者关系(第二部分)

【三者的关系】 首先，辗转相除法可以通过Sylvester矩阵进行，过程如下（以 m 8 、 l 7 m 8、l 7 m8、l7为例子）。 首先调整矩阵中 a a a系数到最后面几行，如下所示： S ( a 8 a 7 a 6 a 5 a 4 a 3 a 2 …...

编程日记 2024/5/27 14:47:56

PyTorch的数据处理

💥今天看一下 PyTorch数据通常的处理方法~ 一般我们会将dataset用来封装自己的数据集，dataloader用于读取数据 Dataset格式说明 💬dataset定义了这个数据集的总长度，以及会返回哪些参数，模板： from tor…...

编程日记 2024/5/27 14:46:53

第14章-蓝牙遥控小车 手把手做蓝牙APP遥控小车 蓝牙串口通讯讲解

本文讲解手机蓝牙如何遥控小车，如何编写串口通信指令 第14章-手机遥控功能 我们要实现蓝牙遥控功能，蓝牙遥控功能要使用:1.单片机的串口、2.蓝牙通信模块 所以我们先调试好:单片机的串口->蓝牙模块->接到一起联调 14.1-电脑控制小车 完成功能…...

编程日记 2024/5/27 14:44:51

【补充1】字节对齐

文章目录 1.字节对齐的基本概念2.字节对齐规则3.实践出真知（加大难度）4 位域 1.字节对齐的基本概念 （1）现代计算机中内存空间都是按照byte划分的， 从理论上讲似乎对任何类型的变量的访问可以从任何地址开始&#xff0…...

编程日记 2024/5/27 14:43:50

Java数据库连接（JDBC）

一、引言 在Java应用程序中，经常需要与数据库进行交互以存储、检索和处理数据。Java数据库连接（JDBC）是Java平台中用于执行这一任务的标准API。JDBC允许Java程序连接到关系数据库，并使用SQL语句来执行查询和更新操作。本教程将详…...

编程日记 2024/5/27 14:42:49

记录一次cas单点登录的集成

主要思路：浏览器访问CAS服务器登录，拿到凭证给后端，后端用此凭证到CAS服务器验证登录并拿到用户信息，之后基于该凭证维持用户的登录状态。 主要流程： 1.浏览器访问后端需认证登录地址（不带ticket&#xf…...

编程日记 2024/5/27 14:40:47

【吊打面试官系列】Java高并发篇 - 什么是乐观锁和悲观锁?

大家好，我是锋哥。今天分享关于 【什么是乐观锁和悲观锁?】面试题，希望对大家有帮助； 什么是乐观锁和悲观锁? 1、乐观锁： 就像它的名字一样，对于并发间操作产生的线程安全问题持乐观状态， 乐观锁认为竞争…...

编程日记 2024/5/27 14:39:46

机器学习之词袋模型

目录 1 词袋模型基本概念 2 词袋模型的表示方法 2.1 三大方法 1 独热表示法（One-Hot） 2 词频表示法（Term Frequency, TF） 3 词频-逆文档频率表示法（TF-IDF） 2.2 例子 1 词袋模型基本概念 词袋模型&a…...

编程日记 2024/5/27 14:38:45

【C++/STL】vector（常见接口、模拟实现、迭代器失效）

🌈个人主页：秦jh_-CSDN博客🔥 系列专栏： https://blog.csdn.net/qinjh_/category_12575764.html?spm1001.2014.3001.5482 目录 简单使用 常见接口 find insert vector模板 模拟实现 尾插 构造 迭代器失效 使用memcpy拷贝问…...

编程日记 2024/5/27 14:37:43

Spring Boot Web 开发：MyBatis、数据库连接池、环境配置与 Lombok 全面解析

推荐一个AI网站，免费使用豆包AI模型，快去白嫖👉海鲸AI 1.0 MyBatis 概述 MyBatis 是一个优秀的持久层框架，它支持自定义 SQL、存储过程以及高级映射。MyBatis 可以帮助我们将数据库操作抽象出来，使得我们的代码更加简洁…...

编程日记 2024/5/27 14:33:39

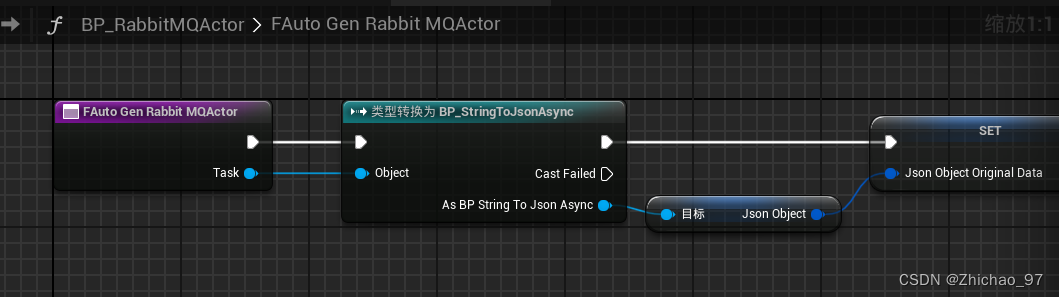
【UE5.1 多线程 异步】“Async Blueprints Extension”插件使用记录

目录 一、异步生成Actor示例 二、异步计算示例 参考视频 首先需要在商城中下载“Async Blueprints Extension”插件 一、异步生成Actor示例 2. 创建一个线程类，这里要指定父类为“LongAsyncTask”、“InfiniteAsyncTask”、“ShortAsyncTask”中的一个 在线程类…...

编程日记 2024/5/27 14:32:38

【已解决】在jupyter里运行torch.cuda.is_available()，显示True，在pycharm中运行却显示false。

文章目录 问题概述1、在Jupyter中GPU运行true2、在pycharm中GPU运行false3、个人解决方案仅供参考 问题概述 在jupyter里运行torch.cuda.is_available()，显示True，在pycharm中运行却显示false。原因在于jupyter 运行环境和pycharm 运行环境不同&#xf…...

编程日记 2024/5/27 14:31:36

Flutter 中的 Scrollbar 小部件：全面指南

Flutter 中的 Scrollbar 小部件：全面指南 在Flutter中，滚动条（Scrollbar）是一种常见的UI组件，用于提供对滚动内容的快速访问和控制。Scrollbar 小部件可以附加到任何可滚动的widget上，如ListView、GridVie…...

编程日记 2024/5/27 14:29:32

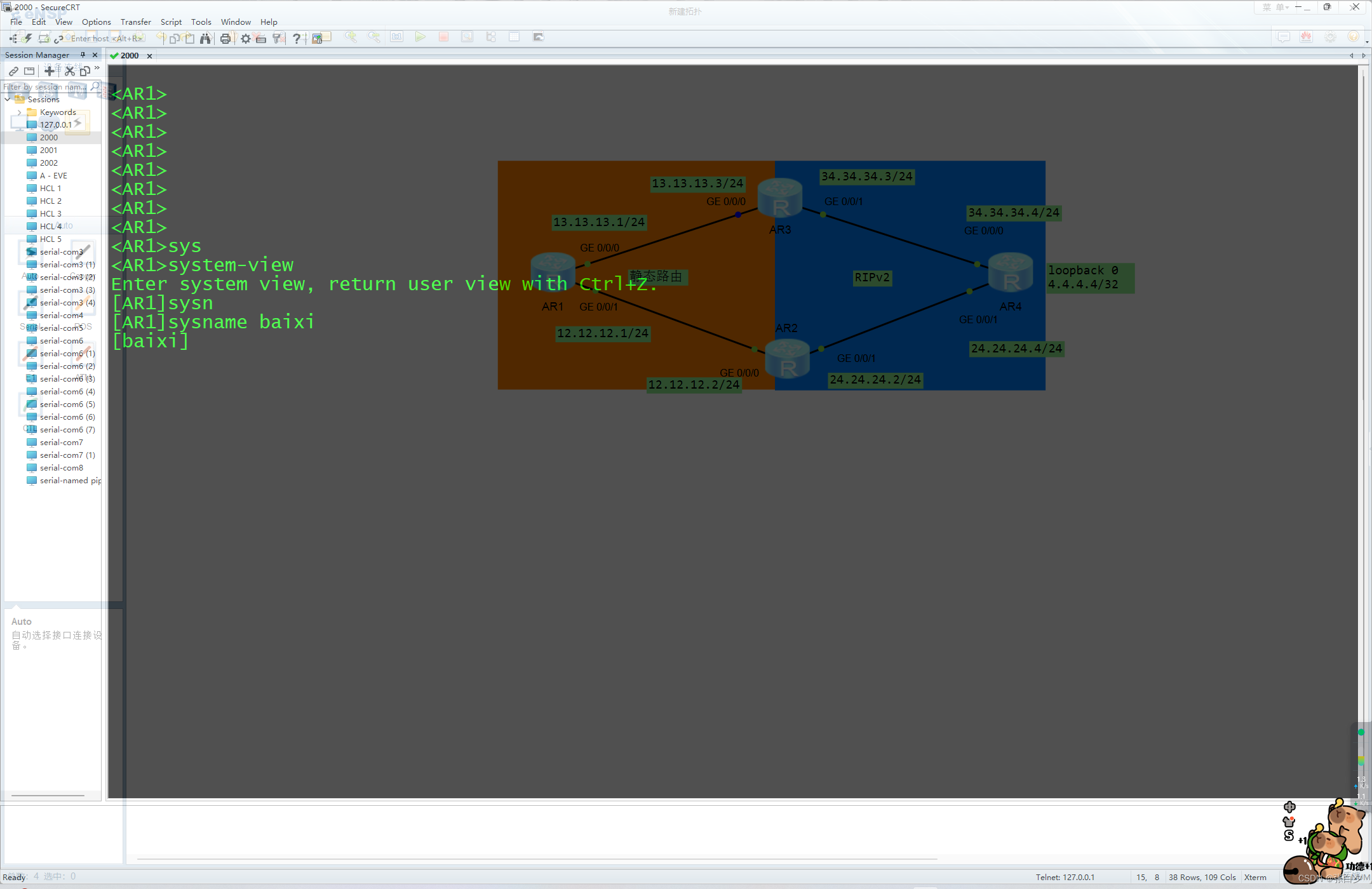
【华为】将eNSP导入CRT，并解决不能敲Tab问题

华为】将eNSP导入CRT，并解决不能敲Tab问题 eNSP导入CRT打开eNSP，新建一个拓扑右键启动查看串口号关联CRT成功界面 SecureCRT连接华为模拟器ensp,Tab键不能补全问题选择Options（选项）-- Global Options （全局选项&#…...

编程日记 2024/5/27 14:28:31

实验二 电子传输系统安全-进展2

上周任务完成情况（代码链接，所写文档等） 重新调通电子公文传输系统部署gmssl学习生成SM2证书学习gmssl中的CTLS实现将数据库从SqlServer迁移到Mysql调试Mysql驱动学习Bouncy Castle 代码链接 Mysql表设计 /* Navicat MySQL Data Transfer…...

编程日记 2024/5/27 14:26:29

JavaScript 获取 HTML 中特定父元素下的子元素

JavaScript 获取 HTML 中特定父元素下的子元素 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <title>查找子元素示例</title> </head> <body><div id"parent"><p&…...

编程日记 2024/5/27 14:22:24

等保服务是一次性服务吗？为什么？怎么理解？

我国等保政策已经严格落地执行&#xff0c;但还有不少企业对于等保服务不是很了解。例如有人问&#xff0c;等保服务是一次性服务吗&#xff1f;为什么&#xff1f;怎么理解&#xff1f;今天我们就来简单回答一下&#xff0c;仅供参考哈&#xff01; 等保服务是一次性服务吗&…...

编程日记 2024/5/27 14:21:23

全网首发UNIAPP功能多的iapp后台源码

全网首发UNIAPP功能多的iapp后台源码&#xff0c;众所周知UN Dev Assist 后台是一款既不免费又不好用的后台今天直接分享。 搭建教程在里面了&#xff0c;自己查看。 源码下载&#xff1a;https://download.csdn.net/download/m0_66047725/89291994 更多资源下载&#xff1a;…...

编程日记 2024/5/27 14:18:21

【搜索方法推荐】高效信息检索方法和实用网站推荐

博主未授权任何人或组织机构转载博主任何原创文章&#xff0c;感谢各位对原创的支持&#xff01; 博主链接 本人就职于国际知名终端厂商&#xff0c;负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作&#xff0c;目前牵头6G算力网络技术标准研究。 博客…...

编程日记 2024/5/27 14:17:19

面试被问到不懂的东西，是直接说不懂还是坚持狡辩一下？

大家好&#xff0c;我是瑶琴呀。 面试被问到不懂的东西&#xff0c;是直接说不懂还是坚持狡辩一下&#xff1f;这个问题可以转变一下&#xff0c;如果你顺利拿到 offer&#xff0c;公司安排的工作跟你之前的技术和经验不匹配&#xff0c;你还愿意干下去吗&#xff1f; 转变一…...

编程日记 2024/5/27 14:16:18

Ubuntu系统下交叉编译openssl

一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机&#xff1a;Ubuntu 20.04.6 LTSHost&#xff1a;ARM32位交叉编译器&#xff1a;arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

编程新知 2025/11/10 15:33:04

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2026/2/8 20:41:48

如何在看板中有效管理突发紧急任务

在看板中有效管理突发紧急任务需要&#xff1a;设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP&#xff08;Work-in-Progress&#xff09;弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中&#xff0c;设立专门的紧急任务通道尤为重要&#xff0c;这能…...

编程新知 2026/2/3 22:50:06

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2026/1/31 13:13:32

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的？

uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件&#xff0c;用于在原生应用中加载 HTML 页面&#xff1a; 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

编程新知 2025/8/6 2:19:46

Java线上CPU飙高问题排查全指南

一、引言 在Java应用的线上运行环境中&#xff0c;CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时&#xff0c;通常会导致应用响应缓慢&#xff0c;甚至服务不可用&#xff0c;严重影响用户体验和业务运行。因此&#xff0c;掌握一套科学有效的CPU飙高问题排查方法&…...

编程新知 2025/11/2 5:30:15

windows系统MySQL安装文档

概览&#xff1a;本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容&#xff0c;为学习者提供全面的操作指导。关键要点包括&#xff1a; 解压 &#xff1a;下载完成后解压压缩包&#xff0c;得到MySQL 8.…...

编程新知 2026/2/6 10:22:29

Qt 事件处理中 return 的深入解析

Qt 事件处理中 return 的深入解析 在 Qt 事件处理中&#xff0c;return 语句的使用是另一个关键概念&#xff0c;它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别&#xff1a;不同层级的事件处理 方…...

编程新知 2025/6/10 21:19:52

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态

前言 在人工智能技术飞速发展的今天&#xff0c;深度学习与大模型技术已成为推动行业变革的核心驱动力&#xff0c;而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心&#xff0c;系统性地呈现了两部深度技术著作的精华&#xff1a;…...

编程新知 2026/2/5 4:33:51

华为OD最新机试真题-数组组成的最小数字-OD统一考试（B卷）

题目描述 给定一个整型数组，请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3，则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组，0<数组长度<= 100，0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

编程新知 2025/9/21 23:43:15