[大师C语言(第十二篇)]C语言堆排序技术详解
引言
堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构的特点来进行排序。堆是一种近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。堆排序是一种不稳定的排序算法,其时间复杂度为O(nlogn),在处理大数据集时效率较高。
第一部分:堆的基本概念与性质
1.1 堆的定义
堆是一种特殊的完全二叉树,它满足两个性质:
- 结构性:堆是一个完全二叉树,即树中的每一层都是满的,除了可能的最后一层,最后一层的节点从左到右排列。
- 堆序性:对于最大堆(Max Heap)来说,每个父节点的值都大于或等于其子节点的值;对于最小堆(Min Heap)来说,每个父节点的值都小于或等于其子节点的值。
1.2 堆的存储
堆通常使用数组来存储,这是因为堆是一种完全二叉树,而完全二叉树非常适合用数组来表示。对于数组中的任意位置i的元素,其左子节点的位置为2i+1,右子节点的位置为2i+2,父节点的位置为(i-1)/2。
1.3 堆的操作
堆的基本操作包括:
- 初始化:创建一个空堆。
- 插入:向堆中插入一个新元素。
- 删除:从堆中删除一个元素。
- 建立堆:将一个无序的数组转换为堆。
- 堆排序:利用堆进行排序。
1.4 堆的建立
建立堆的过程是将一个无序的完全二叉树调整为堆的过程。这个过程通常从最后一个非叶子节点开始,逐个节点进行“下沉”操作,直到根节点。
1.5 代码实现:建立堆
以下是建立最大堆的C语言代码示例:
#include <stdio.h>void heapify(int arr[], int n, int i) {int largest = i; // 初始化最大元素索引为根节点int left = 2 * i + 1; // 左子节点int right = 2 * i + 2; // 右子节点// 如果左子节点大于根节点if (left < n && arr[left] > arr[largest])largest = left;// 如果右子节点大于最大元素if (right < n && arr[right] > arr[largest])largest = right;// 如果最大元素不是根节点,交换之if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;// 递归地调整受影响的子树heapify(arr, n, largest);}
}void buildHeap(int arr[], int n) {// 从最后一个非叶子节点开始,逐个进行堆化for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);buildHeap(arr, n);printf("建立的最大堆: \n");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}
1.6 结论
堆是一种高效的数据结构,它可以用于实现优先队列,也可以用于排序算法。在第一部分中,我们介绍了堆的基本概念、存储方式、基本操作以及如何建立堆。在接下来的两部分中,我们将深入探讨堆排序算法的具体实现和性能分析。请继续关注,以获得更全面的技术解析。
第二部分:堆排序算法的实现
2.1 算法概述
堆排序(Heap Sort)是一种基于堆的排序算法。它将数组转换成一个最大堆,然后将堆顶元素(即最大元素)与堆底元素交换,然后减少堆的大小,对剩余的堆进行堆化。重复这个过程,直到堆的大小为1,此时数组已经有序。
2.2 算法步骤
堆排序的步骤如下:
- 建立堆:将输入的数组转换成一个最大堆。
- 交换堆顶与堆底:将堆顶元素(最大元素)与堆底元素交换,然后将堆的大小减1,这样最大元素就被放到了数组的末尾。
- 堆化剩余元素:对剩下的堆进行堆化,以保持最大堆的性质。
- 重复步骤2和3:重复交换堆顶与堆底元素,并堆化剩余元素,直到堆的大小为1。
2.3 代码实现
以下是堆排序的C语言实现:
#include <stdio.h>void heapify(int arr[], int n, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < n && arr[left] > arr[largest])largest = left;if (right < n && arr[right] > arr[largest])largest = right;if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;heapify(arr, n, largest);}
}void heapSort(int arr[], int n) {// 建立最大堆for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 一个个从堆顶取出元素for (int i = n - 1; i >= 0; i--) {// 移动当前根节点到数组末尾int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 对剩余的堆进行堆化heapify(arr, i, 0);}
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);heapSort(arr, n);printf("排序后的数组: \n");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}
2.4 算法分析
- 时间复杂度:堆排序的时间复杂度为O(nlogn),其中n是数组的长度。建立堆的时间复杂度为O(n),每次堆化的时间复杂度为O(logn),共需进行n-1次堆化。
- 空间复杂度:堆排序是原地排序算法,除了交换元素需要常数级的额外空间外,不需要额外的存储空间,因此空间复杂度为O(1)。
- 稳定性:堆排序是不稳定的排序算法,因为相同值的元素可能会因为堆化操作而改变它们的相对顺序。
2.5 结论
堆排序是一种高效的排序算法,特别适合于数据量较大的情况。它的主要优点是时间复杂度较低,且空间复杂度为常数级别。然而,由于其不稳定性,在某些特定场景下可能会受到影响。在第三部分中,我们将比较堆排序与其他排序算法的性能,并讨论堆排序在实际应用中的适用性。请继续关注,以获得更全面的技术解析。
第三部分:堆排序的性能比较与应用分析
3.1 性能比较
堆排序与其他排序算法相比,具有以下特点:
- 时间复杂度:堆排序的时间复杂度为O(nlogn),这与快速排序和归并排序的最佳和平均情况下的时间复杂度相同。但是,快速排序在实际应用中通常更快,因为它的内部循环可以有效地在内存中执行。归并排序则需要额外的存储空间,但在处理链表时更为高效。
- 空间复杂度:堆排序是原地排序算法,空间复杂度为O(1),这与快速排序相同。归并排序的空间复杂度为O(n),因为它需要额外的存储空间来合并两个有序数组。
- 稳定性:堆排序是不稳定的排序算法,这与快速排序相同。归并排序是稳定的,因为它会保持相等元素的原始顺序。
- 最坏情况:堆排序的最坏情况时间复杂度为O(nlogn),而快速排序在最坏情况下的时间复杂度为O(n^2)。归并排序的最坏情况时间复杂度也是O(nlogn)。
3.2 应用分析
堆排序在以下场景中特别有用:
- 内存限制严格:由于堆排序是原地排序,它不需要额外的存储空间,因此在内存受限的环境中非常适用。
- 数据量大:当数据量非常大时,堆排序的时间复杂度优势使其成为一个高效的选择。
- 实时系统:在实时系统中,堆排序的确定性时间复杂度使其成为一个可靠的选择,因为它可以提供一致的性能。
然而,堆排序也有其局限性:
- 不稳定性:对于需要保持相等元素原始顺序的应用,堆排序可能不是最佳选择。
- 常数因子:尽管堆排序的时间复杂度与快速排序和归并排序相同,但它的常数因子通常较大,这意味着在实际应用中可能比其他排序算法慢。
3.3 结论
堆排序是一种高效的排序算法,特别适合于数据量大且内存受限的环境。它的主要优势在于其时间复杂度和空间复杂度。然而,由于其不稳定性以及可能的性能问题,堆排序可能不是所有场景下的最佳选择。在选择排序算法时,应该考虑数据的特性和应用的需求,以确定最合适的排序算法。
通过本文的三个部分,我们详细介绍了堆排序的原理、实现和性能分析。堆排序作为一种高效的排序算法,在特定场景下仍然是一个非常有用的工具。然而,它并不是万能的,了解其优势和局限性对于在实际应用中选择合适的排序算法至关重要。希望本文能够为读者提供深入的技术见解,帮助更好地理解和应用堆排序。
相关文章:
]C语言堆排序技术详解)
[大师C语言(第十二篇)]C语言堆排序技术详解
引言 堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构的特点来进行排序。堆是一种近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父…...

Activity启动流程要点
一、Activity启动流程 Activity的启动流程一般是通过调用startActivity或者是startActivityForResult来开始的startActivity内部也是通过调用startActivityForResult来启动Activity,只不过传递的requestCode小于0Activity的启动流程涉及到多个进程之间的通讯这里主…...

lua 计算第几周
需求 计算当前赛季的开始和结束日期,2024年1月1日周一是第1周的开始,每两周是一个赛季。 lua代码 没有处理时区问题 local const 24 * 60 * 60 --一整天的时间戳 local server_time 1716595200--todo:修改服务器时间 local date os.date("*t…...
负载均衡策略
...

海外网红营销新趋势:“快闪式”营销如何迅速提升品牌曝光度
在当今数字化时代,海外网红营销已成为品牌迅速触达全球消费者、提升品牌曝光度和刺激销售的重要手段。其中,“快闪式”营销以其独特的时效性、创意性和互动性,成为品牌与海外网红合作的新趋势。本文Nox聚星将和大家探讨如何利用海外网红的影响…...

速看!打造专属数字化能力模型的七大关键!
在数字化浪潮中,企业如何打造适应自身发展的数字化能力模型?这是许多企业面临的重要课题。今天,通过众多企业使用蚓链数字化生态解决方案实践总结,为大家分享至关重要的七大经验,助你开启数字化转型之旅! 1…...

青蛙跳台阶问题
本期介绍🍖 主要介绍:青蛙跳台阶问题,青蛙跳台阶与斐波那契数列的关系👀。 文章目录 1. 题目2. 递归解题思路3. 迭代解题思路 1. 题目 从前有一只青蛙他想跳台阶,有n级台阶,青蛙一次可以跳1级台阶ÿ…...

linux日常运维2
下载linux离线安装包---- 利用 Downloadonly 插件下载 RPM 软件包及其所有依赖包 1. 先找个可以上网的linux操作系统,这里是以centos7操作系统为例,如果要使用centos6就先安装一个centos6的系统,然后让他可以上网,后面步骤如下 a.…...
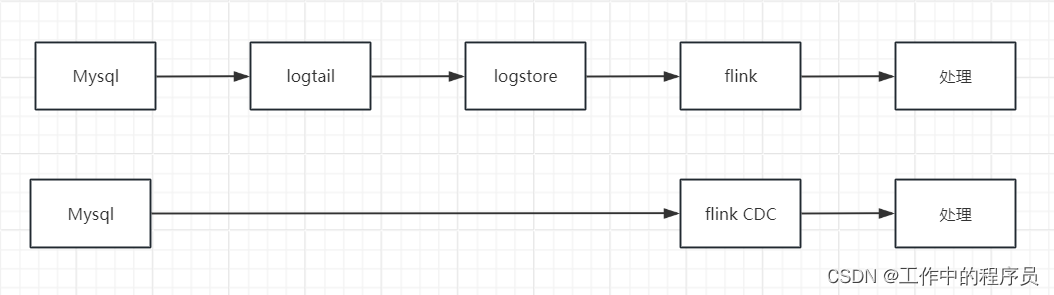
flink cdc mysql整理与总结
文章目录 一、业务中常见的需要数据同步的场景CDC是什么FlinkCDC是什么CDC原理为什么是FlinkCDC业务场景flink cdc对应flink的版本 二、模拟案例1.阿里云flink sql2.开源flink sql(单机模式)flink 安装安装mysql3.flink datastream 三、总结 提示:以下是本篇文章正文…...
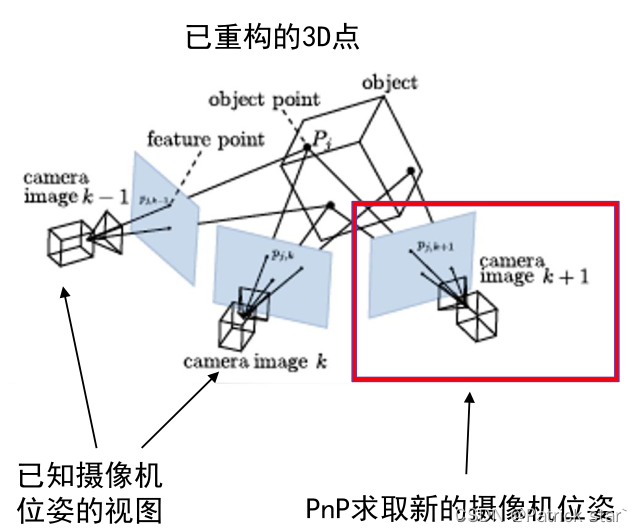
【三维重建】ePnP
PnP问题应用与一下场景: 已知三维点和对应二维点以及相机相机内参数,可以获取相机外参。 我们介绍其中的一种算法:ePnP 算法流程 1、ePnP算法首先在世界坐标系内寻找4个控制点,记作 C 1 w , C 2 w , C 3 w , C 4 w C_1^w,C_2^w,…...

C++进阶之路:何为运算符重载、赋值运算符重载与前后置++重载(类与对象_中篇)
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
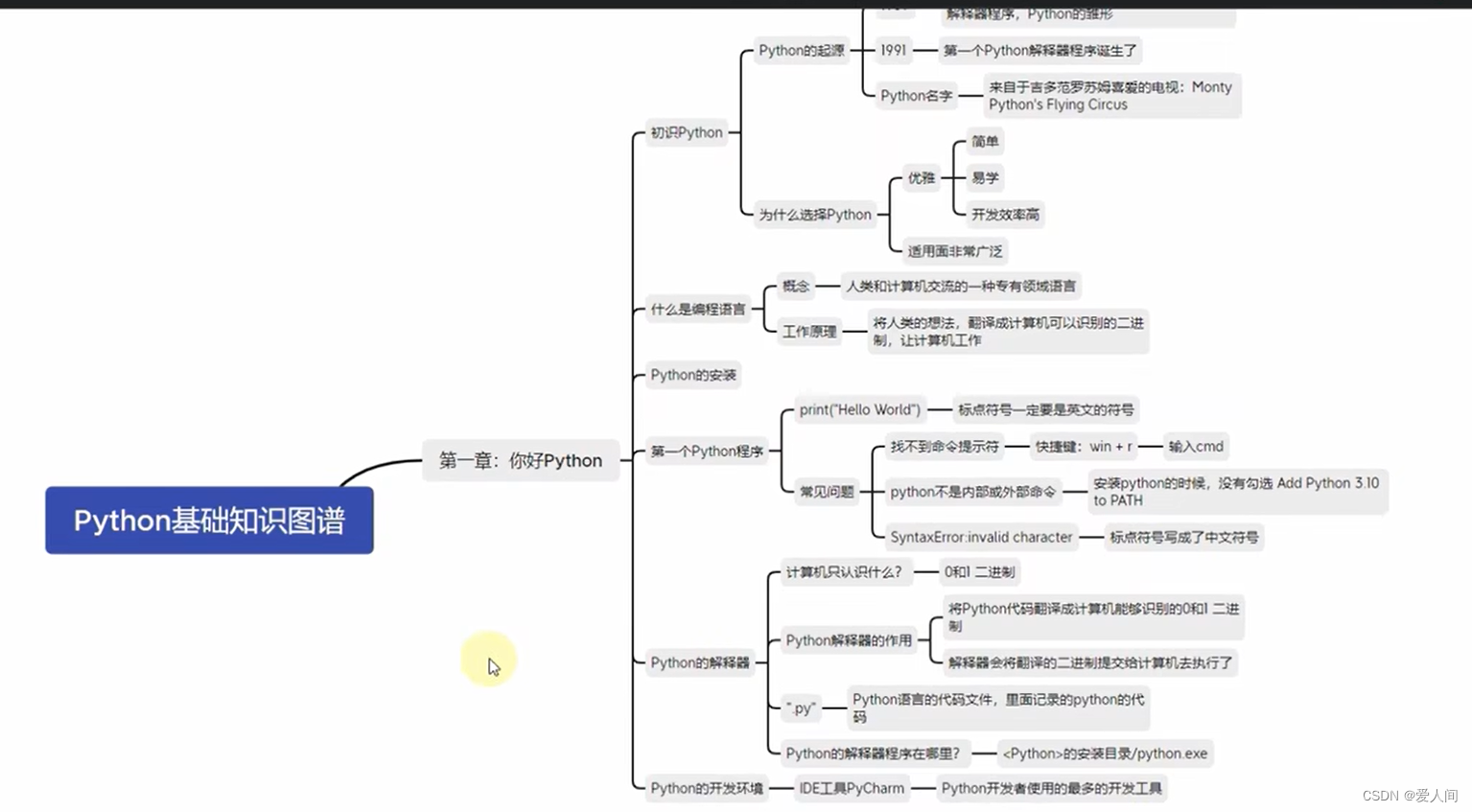
8、python基础知识图谱
...

智慧校园建设规划方案
在信息化浪潮的推动下,智慧校园的建设已成为教育现代化的必然趋势。以创新科技赋能教育,打造智慧校园,旨在提升教学品质,优化管理流程,增强学生体验。构建智慧校园需要具有前瞻性的规划方案,它将以教育为核…...

【深度学习实战—8】:基于MediaPipe的人脸检测
✨博客主页:王乐予🎈 ✨年轻人要:Living for the moment(活在当下)!💪 🏆推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】 目录 😺一、Med…...

OSCP学习,布置你的Kali Linux
为什么要写这篇文章? 我是一个OSCP学习者,以教促学。同时也能让各位入门的师傅们更好的了解OSCP这门课程。本人文笔不太好,如果有什么写的不对的地方,师傅们多多指正。 参考资料: OSCP 考试电子书 Linux Basics for…...

PWA离线优先策略:提升用户体验的关键步骤
Progressive Web Apps (PWA) 的离线优先策略是通过Service Worker和Cache API实现的,它允许在没有网络连接时仍然可以访问网站的部分或全部内容。 2500G计算机入门到高级架构师开发资料超级大礼包免费送! 1. 创建Service Worker注册文件(se…...
网页提示“非私密连接”是为什么?
网页提示“非私密连接”(英文提示可能是 "Your connection is not private" 或 "Your connection is not secure")主要是因为浏览器无法验证你正试图访问的网站的SSL/TLS证书,或者是证书存在问题,从而无法建立…...

[自动驾驶技术]-8 Tesla自动驾驶方案之硬件(AI Day 2022)
特斯拉在AI Day 2022先介绍了AI编译器,后面又介绍了Dojo的硬件软件,软件部分和AI编译器有部分重叠,本文介绍还是延用AI Day的思路,分为三部分:AI编译和推理,Dojo硬件,Dojo软件。 特斯拉车道检测…...

人力资源管理信息化系统如何支持企业开展管理诊断?
华恒智信人力资源顾问有限公司致力于帮助企业开展人力资源管理方面的各项提升改进工作,在长期的咨询工作中,最常听到企业提到的问题莫过于管理诊断方面的问题,事实上,很多企业在日常工作中,都意识到企业内部存在管理方…...
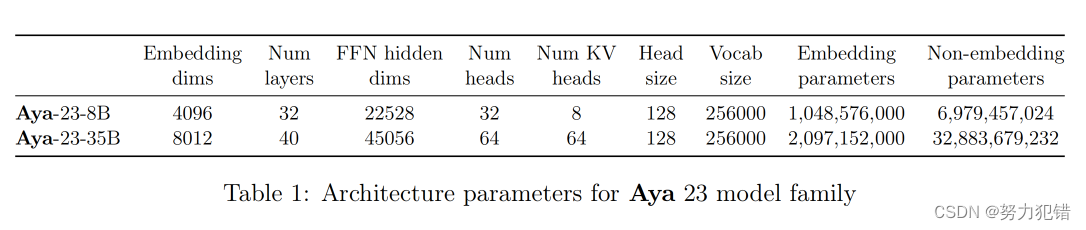
Cohere继Command-R+之后发布大模型Aya-23,性能超越 Gemma、Mistral 等,支持中文
前言 近年来,多语言大模型(MLLM)发展迅速,但大多数模型的性能依然存在显著差距,尤其是在非英语语言方面表现不佳。为了推动多语言自然语言处理技术的发展,Cohere团队发布了新的多语言指令微调模型家族——…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
