python九九乘法表的打印思考及实现

新书上架~👇全国包邮奥~

python实用小工具开发教程![]() http://pythontoolsteach.com/3
http://pythontoolsteach.com/3
欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~
目录
一、问题引入
九九乘法表的显示需求
二、问题分析
嵌套循环的概念
屏幕宽度与换行的考虑
三、代码实现
伪代码示例
代码实现细节
四、总结与思考
嵌套循环的重要性
屏幕宽度的适应性问题
编程实践的意义

一、问题引入
九九乘法表的显示需求
- 需求描述:文档提到了一个关于打印九九乘法表的问题,需要实现一种特定的打印效果,同时考虑了屏幕宽度限制导致的换行问题。
- 效果展示:示例中的乘法表显示格式是1×1=1, 1×2=2, ..., 直到 9×9=81,中间用制表符分隔,并在适当位置加入换行符以适应屏幕宽度。
二、问题分析
嵌套循环的概念
- 嵌套循环的定义:嵌套循环指的是在一个循环体内又包含另一个完整的循环结构,也称为循环嵌套。
- 在打印乘法表中的应用:通过使用两个嵌套的for循环,外层循环控制行数(乘数),内层循环控制列数(被乘数),可以实现九九乘法表的打印。
屏幕宽度与换行的考虑
- 换行的原因:由于屏幕宽度的限制,当打印的内容超过一定长度时,会自动换行。
- 解决方案:通过控制每行的输出长度,当达到预设的阈值时手动添加换行符,以确保打印效果的整洁和可读性。
三、代码实现
伪代码示例
for i in range(1, 10): # 外层循环,控制行数(乘数) for j in range(1, i+1): # 内层循环,控制列数(被乘数) print(f"{i}×{j}={i*j}", end="\t") # 输出乘法表达式,用制表符分隔 if 某个条件判断是否需要换行: # 例如,当当前列数达到某个阈值或输出长度超过屏幕宽度时 print() # 手动换行代码实现细节
- end参数的使用:在print函数中,通过设置end参数为"\t"(制表符),可以实现乘法表达式之间的水平分隔。
- 换行条件的判断:根据实际需求,可以通过设置固定的列数阈值或动态计算输出长度来判断是否需要换行。
- 输出格式的调整:可以根据需要调整乘法表达式的输出格式,如添加空格、边框等,以提高可读性和美观性。
四、总结与思考
嵌套循环的重要性
- 嵌套循环是编程中常见的控制结构之一,通过合理使用嵌套循环可以高效解决许多复杂的问题。
- 在打印九九乘法表这样的任务中,嵌套循环的应用展示了其强大的功能性和灵活性。
屏幕宽度的适应性问题
- 在编写输出类的程序时,需要考虑输出设备(如屏幕)的限制因素,如宽度、高度等。
- 通过合理的算法设计和输出控制,可以实现输出内容的自适应调整,以适应不同设备的显示需求。
编程实践的意义
- 通过实践九九乘法表的打印任务,不仅可以巩固嵌套循环等基础知识,还可以提高解决实际问题的能力。
- 编程实践是理论知识与实际应用相结合的重要途径,有助于提升个人的编程技能和综合素质。
非常感谢您花时间阅读我的博客,希望这些分享能为您带来启发和帮助。期待您的反馈与交流,让我们共同成长,再次感谢!
👇热门内容👇
python使用案例与应用_安城安的博客-CSDN博客
软硬件教学_安城安的博客-CSDN博客
Orbslam3&Vinsfusion_安城安的博客-CSDN博客
网络安全_安城安的博客-CSDN博客
教程_安城安的博客-CSDN博客
python办公自动化_安城安的博客-CSDN博客
👇个人网站👇
安城安的云世界

相关文章:

python九九乘法表的打印思考及实现
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、问题引入 九九乘法表的显示需求 二、问题分析 嵌套循环的概念 屏幕宽度与换行的考虑…...

2.Spring中用到的设计模式
Spring框架中使用了多种设计模式来构建其强大且灵活的功能,这里举例说明Spring中的一些功能使用到的设计模式。 工厂模式:Spring容器本质是一个大工厂,使用工厂模式通过BeanFactory和ApplicationContext这两个核心接口来创建和管理bean对象。…...
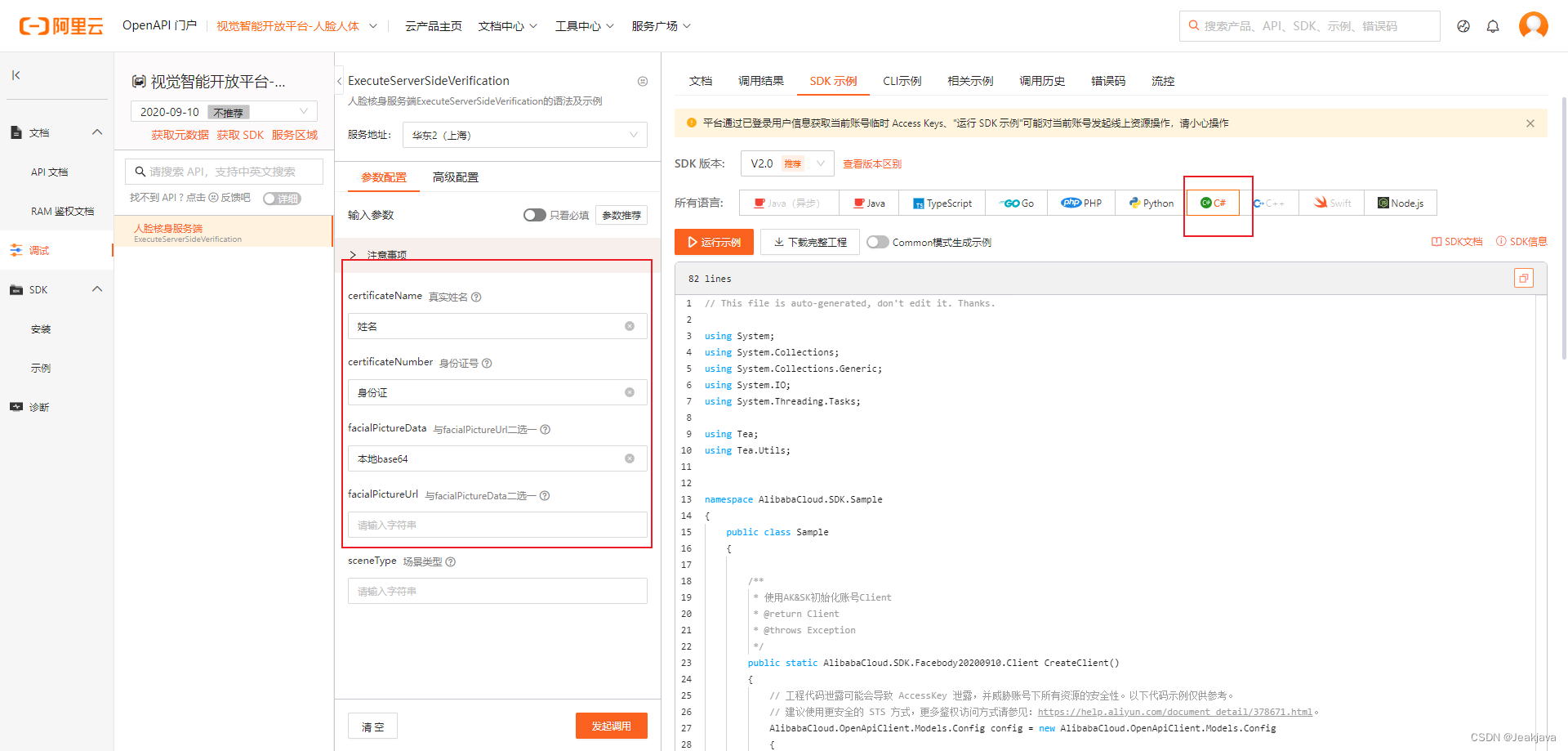
.NET调用阿里云人脸核身服务端 (ExecuteServerSideVerification)简易流程保姆级教学
需要注意的是,以下内容仅限基础调用 功能说明 该功能是输入核验人的姓名和身份证以及人脸照片,去阿里库里面匹配,3个信息是否一致,一致则验证通过,需要注意的是,人脸有遮挡,或者刘海࿰…...
]C语言堆排序技术详解)
[大师C语言(第十二篇)]C语言堆排序技术详解
引言 堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构的特点来进行排序。堆是一种近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父…...

Activity启动流程要点
一、Activity启动流程 Activity的启动流程一般是通过调用startActivity或者是startActivityForResult来开始的startActivity内部也是通过调用startActivityForResult来启动Activity,只不过传递的requestCode小于0Activity的启动流程涉及到多个进程之间的通讯这里主…...

lua 计算第几周
需求 计算当前赛季的开始和结束日期,2024年1月1日周一是第1周的开始,每两周是一个赛季。 lua代码 没有处理时区问题 local const 24 * 60 * 60 --一整天的时间戳 local server_time 1716595200--todo:修改服务器时间 local date os.date("*t…...
负载均衡策略
...

海外网红营销新趋势:“快闪式”营销如何迅速提升品牌曝光度
在当今数字化时代,海外网红营销已成为品牌迅速触达全球消费者、提升品牌曝光度和刺激销售的重要手段。其中,“快闪式”营销以其独特的时效性、创意性和互动性,成为品牌与海外网红合作的新趋势。本文Nox聚星将和大家探讨如何利用海外网红的影响…...

速看!打造专属数字化能力模型的七大关键!
在数字化浪潮中,企业如何打造适应自身发展的数字化能力模型?这是许多企业面临的重要课题。今天,通过众多企业使用蚓链数字化生态解决方案实践总结,为大家分享至关重要的七大经验,助你开启数字化转型之旅! 1…...

青蛙跳台阶问题
本期介绍🍖 主要介绍:青蛙跳台阶问题,青蛙跳台阶与斐波那契数列的关系👀。 文章目录 1. 题目2. 递归解题思路3. 迭代解题思路 1. 题目 从前有一只青蛙他想跳台阶,有n级台阶,青蛙一次可以跳1级台阶ÿ…...

linux日常运维2
下载linux离线安装包---- 利用 Downloadonly 插件下载 RPM 软件包及其所有依赖包 1. 先找个可以上网的linux操作系统,这里是以centos7操作系统为例,如果要使用centos6就先安装一个centos6的系统,然后让他可以上网,后面步骤如下 a.…...
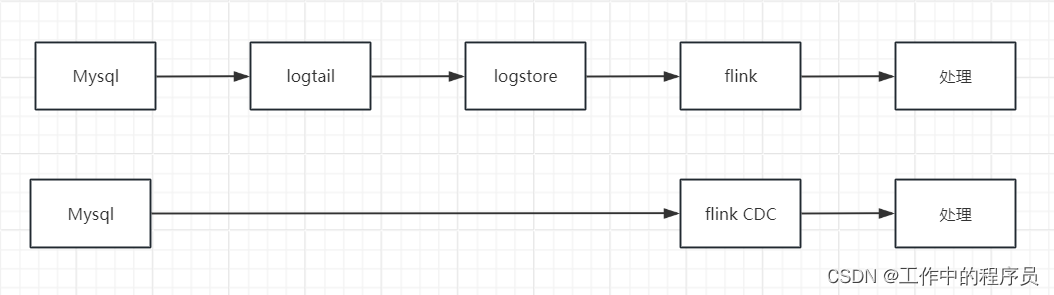
flink cdc mysql整理与总结
文章目录 一、业务中常见的需要数据同步的场景CDC是什么FlinkCDC是什么CDC原理为什么是FlinkCDC业务场景flink cdc对应flink的版本 二、模拟案例1.阿里云flink sql2.开源flink sql(单机模式)flink 安装安装mysql3.flink datastream 三、总结 提示:以下是本篇文章正文…...
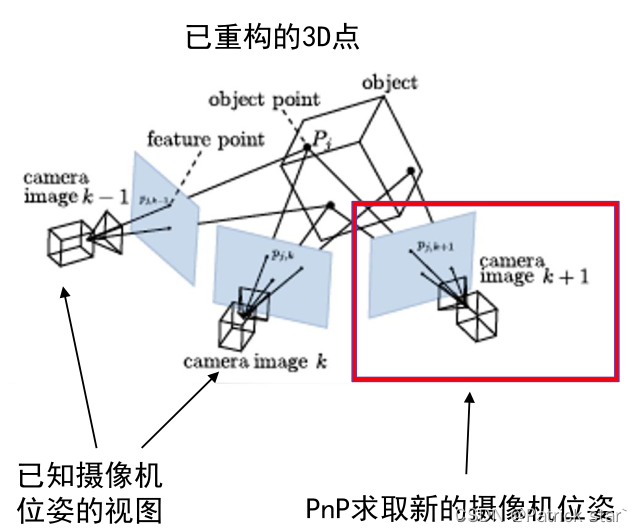
【三维重建】ePnP
PnP问题应用与一下场景: 已知三维点和对应二维点以及相机相机内参数,可以获取相机外参。 我们介绍其中的一种算法:ePnP 算法流程 1、ePnP算法首先在世界坐标系内寻找4个控制点,记作 C 1 w , C 2 w , C 3 w , C 4 w C_1^w,C_2^w,…...

C++进阶之路:何为运算符重载、赋值运算符重载与前后置++重载(类与对象_中篇)
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
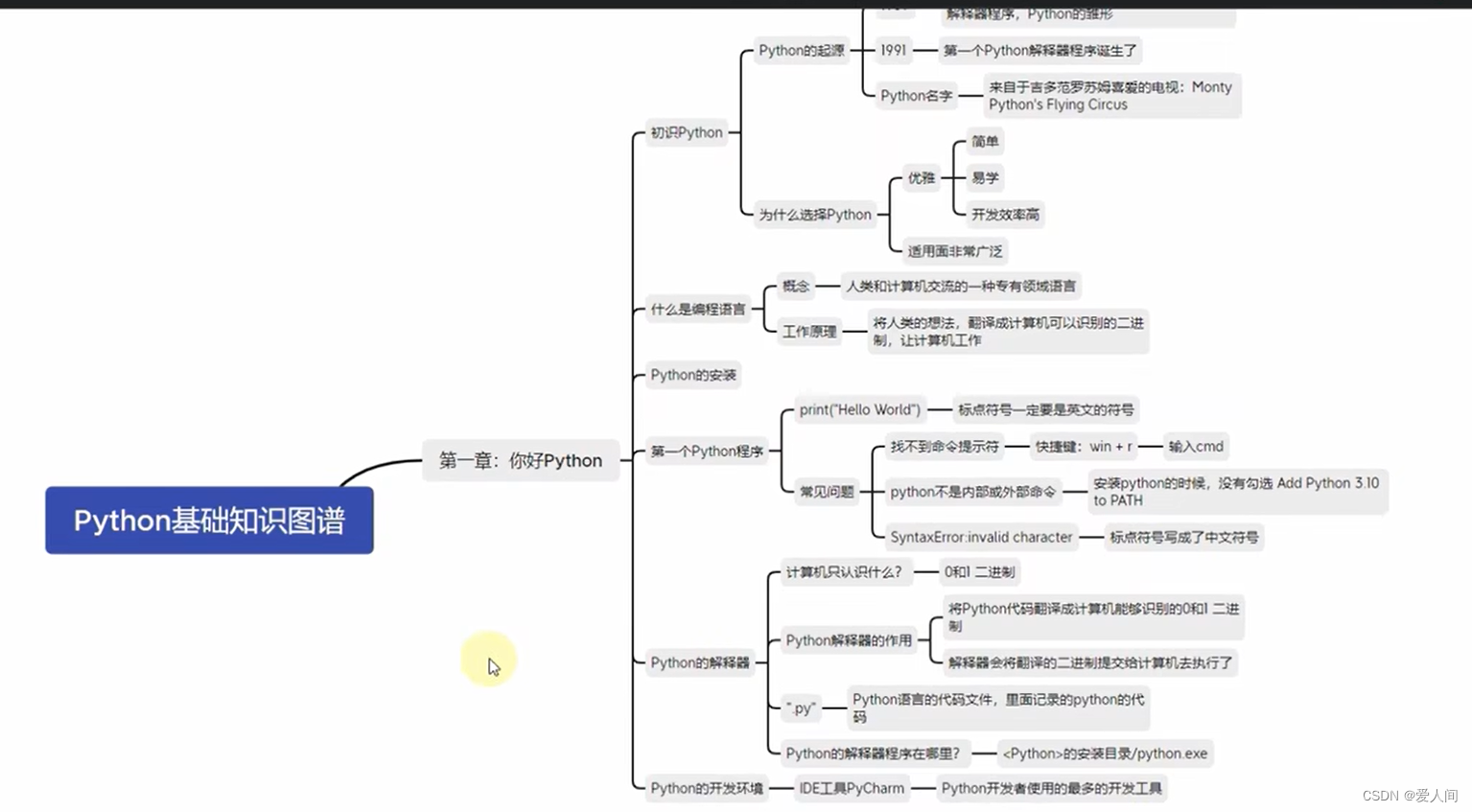
8、python基础知识图谱
...

智慧校园建设规划方案
在信息化浪潮的推动下,智慧校园的建设已成为教育现代化的必然趋势。以创新科技赋能教育,打造智慧校园,旨在提升教学品质,优化管理流程,增强学生体验。构建智慧校园需要具有前瞻性的规划方案,它将以教育为核…...

【深度学习实战—8】:基于MediaPipe的人脸检测
✨博客主页:王乐予🎈 ✨年轻人要:Living for the moment(活在当下)!💪 🏆推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】 目录 😺一、Med…...

OSCP学习,布置你的Kali Linux
为什么要写这篇文章? 我是一个OSCP学习者,以教促学。同时也能让各位入门的师傅们更好的了解OSCP这门课程。本人文笔不太好,如果有什么写的不对的地方,师傅们多多指正。 参考资料: OSCP 考试电子书 Linux Basics for…...

PWA离线优先策略:提升用户体验的关键步骤
Progressive Web Apps (PWA) 的离线优先策略是通过Service Worker和Cache API实现的,它允许在没有网络连接时仍然可以访问网站的部分或全部内容。 2500G计算机入门到高级架构师开发资料超级大礼包免费送! 1. 创建Service Worker注册文件(se…...
网页提示“非私密连接”是为什么?
网页提示“非私密连接”(英文提示可能是 "Your connection is not private" 或 "Your connection is not secure")主要是因为浏览器无法验证你正试图访问的网站的SSL/TLS证书,或者是证书存在问题,从而无法建立…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
