R实验 随机变量及其分布
- 实验目的:
- 掌握常见几种离散性随机变量及其分布在R语言中对应的函数用法;
- 掌握常见几种连续性随机变量及其分布在R语言中对应的函数用法;
- 掌握统计量的定义及统计三大抽样分布在R语言中对应的函数用法。
实验内容:
(习题4.5)通过对学生成绩的统计,高等数学课程的不及格率为20%。现随机地抽查了学习该课程的20名学生,试计算:(提示:这是一个二项分布,参考例4.7)
(1)有2名或2名以下学生不及格的概率是多少?(提示:累积分布函数pbinom(),答案:0.2061)
p1<-pbinom(2,size = 20,prob = 0.2)p1
(2)有4名学生不及格的概率是多少?(提示:概率密度函数dbinom(),答案:0.2182)
p2<-dbinom(4,size = 20,prob = 0.2)p2
(3)超过3名学生不及格的概率是多少?(提示:累积分布函数pbinom(),答案:0.5886)
p3<-pbinom(3,size = 20,prob = 0.2)p4<-1 - p3p4
(习题4.14)设某城市男子的身高服从均值为168cm,标准差为6cm的正态分布。求:
(1)该市男子身高在170cm以上的概率;(提示:累积分布函数pnorm(),答案:0.3694)
p<-pnorm(170,mean = 168,6)p1<-1-pp1
(2)为了使99%以上的男子上公共汽车不至于在车门上沿碰头,当地的公共汽车门框应设计多高?(提示:即求身高为哪个值以下的概率超过0.99,亦即:求k的值,使得P{X≤k}≥.0.99。显然题目是求分位数k,需要用到分位数函数qnorm()。注意到在R语言中,分位数函数默认是下分位数,大家可以看一下,R语言中下分位数函数中有一个参数lower.tail=TRUE,这个参数就是表示下分位数,默认值为TRUE。可参考例4.14。答案:181.9581)
p<-pnorm(170,mean = 168,6)p1<-1-pp1
按照参考代码,在一个图中绘制如下图所示的三个正态分布的概率密度函数曲线。要求(第4-7题要求与此类似,不再重复说明):
(1)生成图形后,点击RStudio右下角区域中的“Plot”标签下的“Export”按钮,在弹出的菜单中选择“Save as Image…”,保存为PNG格式。然后将此PNG图片插入到此文档中,替换掉原来的样例图。
(2)删除参考代码截图,并粘贴代码文字到此文档中(不是截图)。
(3)对其中的一些参数,可以修改其值或者注释掉该参数,看看生成的图形有什么变化,从而加深理解这些参数的意义。
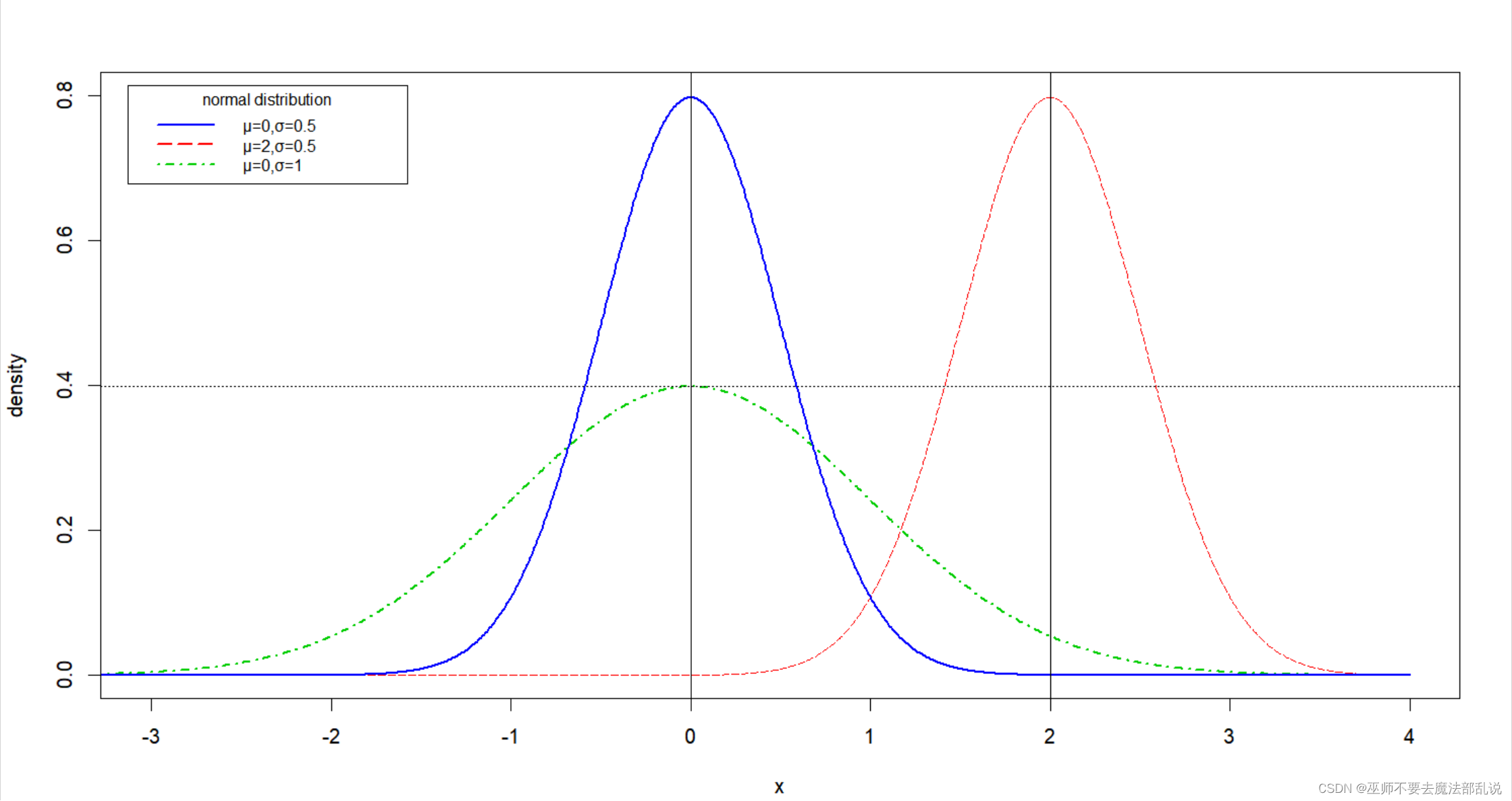
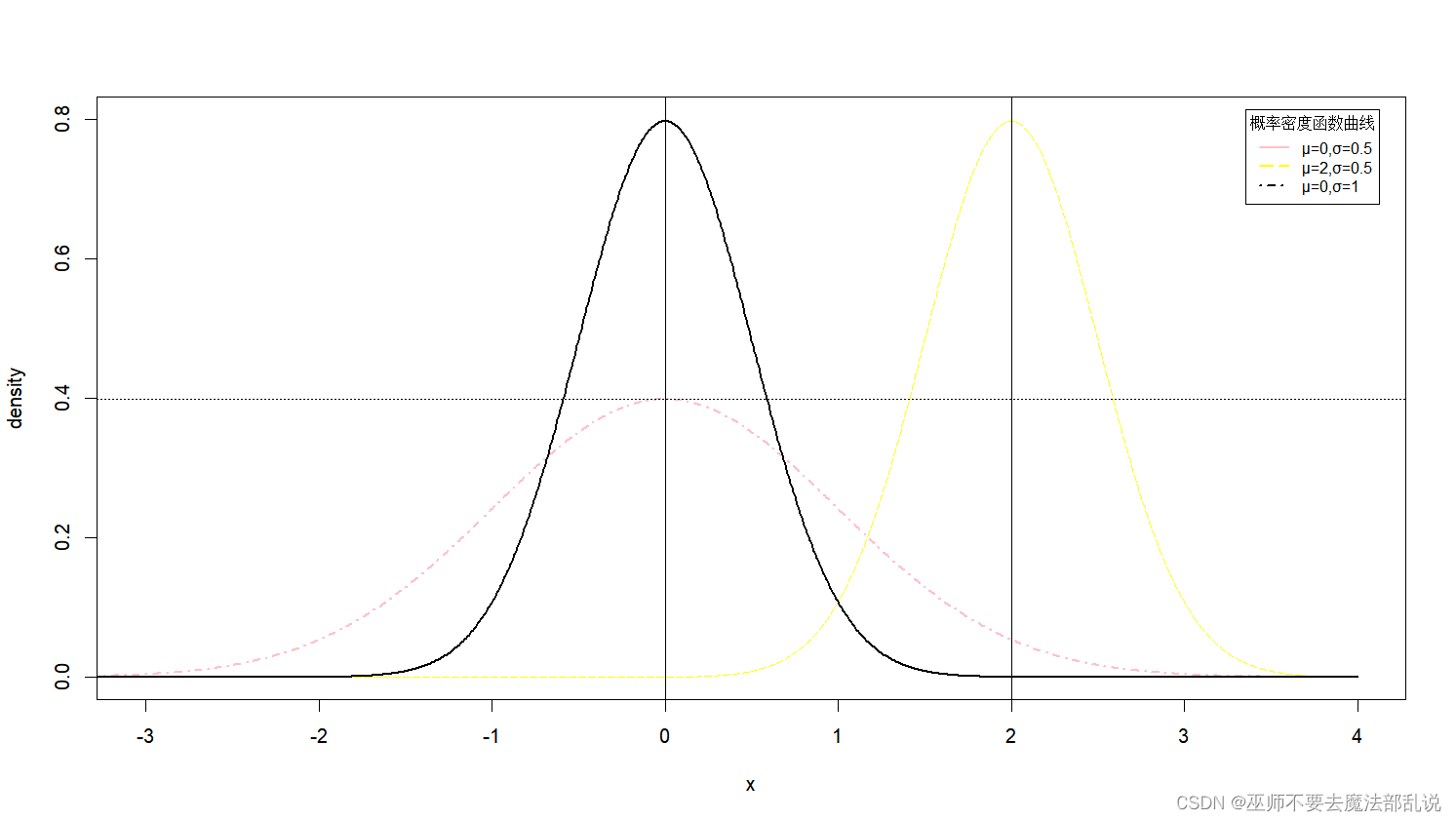
参考代码:
x <- seq(-4,4,length.out =1000)y1 <- dnorm(x)y2 <- dnorm(x,mean = 2,sd = 0.5)y3 <-dnorm(x,mean = 0,sd = 0.5)plot(x,y1,type = "l",lty =4,col ="green3",lwd = 2,xlim = c(-3,4),ylim = c(0,0.8),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n",)lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1,at = seq(-3,4,by = 1))axis(side = 2,at = seq(0,0.8,by = 0.2))abline(v = 0)abline(v = 2)abline(h = max(y1),lty = 3)legend("topleft",inset = 0.02,title = "normal distribution",c("μ=0,σ=0.5","μ=2,σ=0.5","μ=0,σ=1"),cex = 0.8,lty = c(1,5,4),lwd = 2,col = c("blue","red","green3"))在一个图中,绘制第3题中三个正态分布函数的累积分布函数曲线。(注意为了让曲线完整显示,纵轴的范围需要调整为0到1之间,同时将纵坐标的标签改为CDF,即累积分布函数(Cumulative Distribution Function))

替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(-4,4,length.out =1000)y1 <- pnorm(x)y2 <- pnorm(x,mean = 2,sd = 0.5)y3 <-pnorm(x,mean = 0,sd = 0.5)plot(x,y1,type = "l",lty =4,col ="green",lwd = 2,xlim = c(-4,4),ylim = c(0,1),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n",)lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1,at = seq(-4,4,by = 2))axis(side = 2,at = seq(0,1,by = 0.2))abline(v = 0)abline(v = 2)#abline(h = max(y1),lty = 3)legend("topleft",inset = 0.02,title = "累积密度函数曲线",c("μ=0,σ=0.5","μ=2,σ=0.5","μ=0,σ=1"),cex = 0.8,lty = c(1,5,4),lwd = 2,col = c("blue","red","green3"))模仿第3题,绘制下图所示的三个c2分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化)
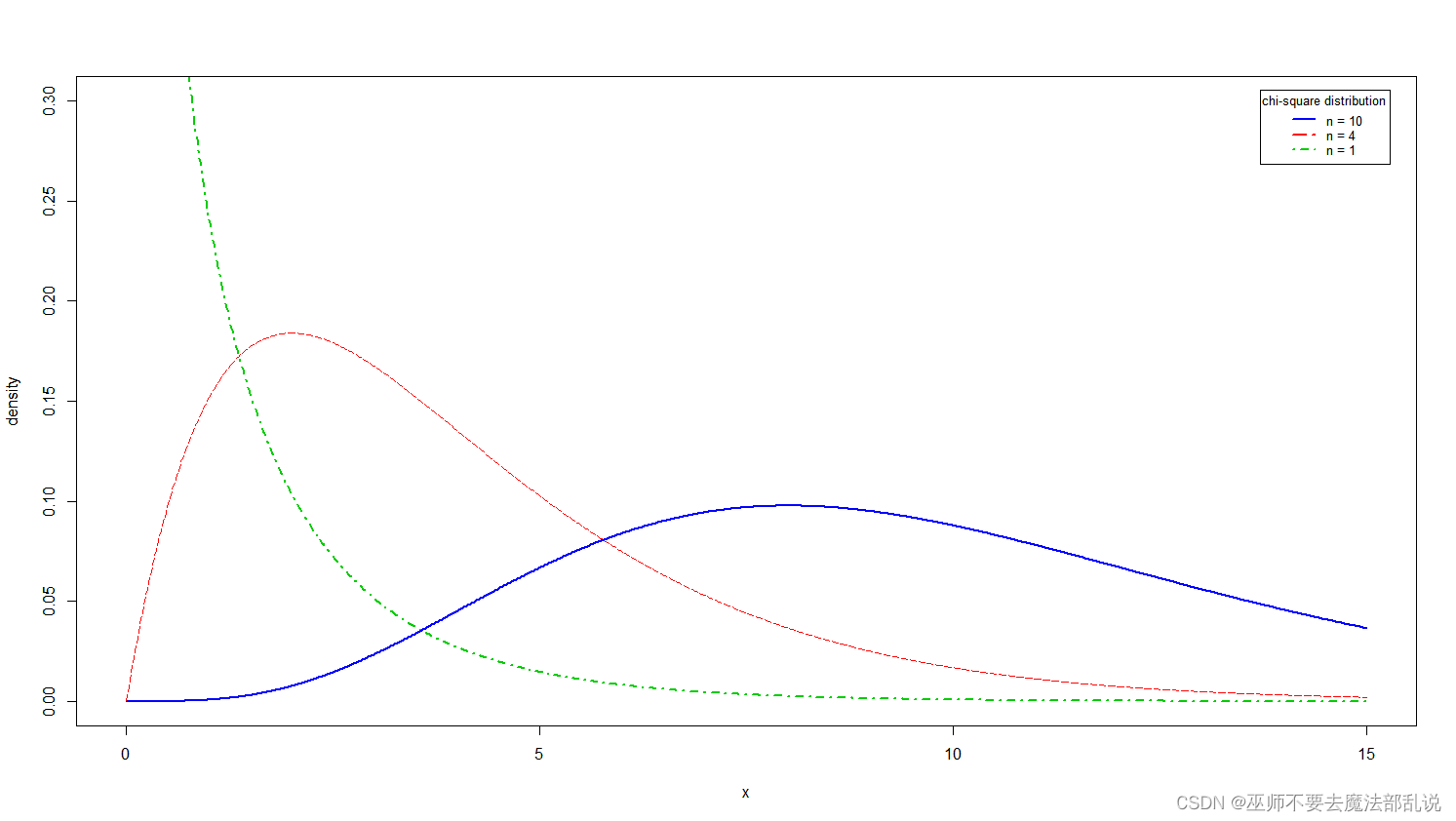
替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(0,15, length.out = 1000)y1 <- dchisq(x, df = 1)y2 <- dchisq(x, df = 4)y3 <- dchisq(x, df = 10)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 15),ylim = c(0.00, 0.30),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 15, by = 5))axis(side = 2, at = seq(0, 0.30, by = 0.05))#abline(v = 0)#abline(v = 2)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "chi-square distribution",c("n = 10", "n = 4", "n = 1"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("blue", "red", "green3"))模仿第3题,绘制下图所示的三个t分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化)

替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(0,15, length.out = 1000)y1 <- dchisq(x, df = 1)y2 <- dchisq(x, df = 4)y3 <- dchisq(x, df = 10)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 15),ylim = c(0.00, 0.30),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 15, by = 5))axis(side = 2, at = seq(0, 0.30, by = 0.05))#abline(v = 0)#abline(v = 2)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "chi-square distribution",c("n = 10", "n = 4", "n = 1"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("blue", "red", "green3"))模仿第3题,绘制下图所示的三个F分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化。图例中字符的下标不做要求)
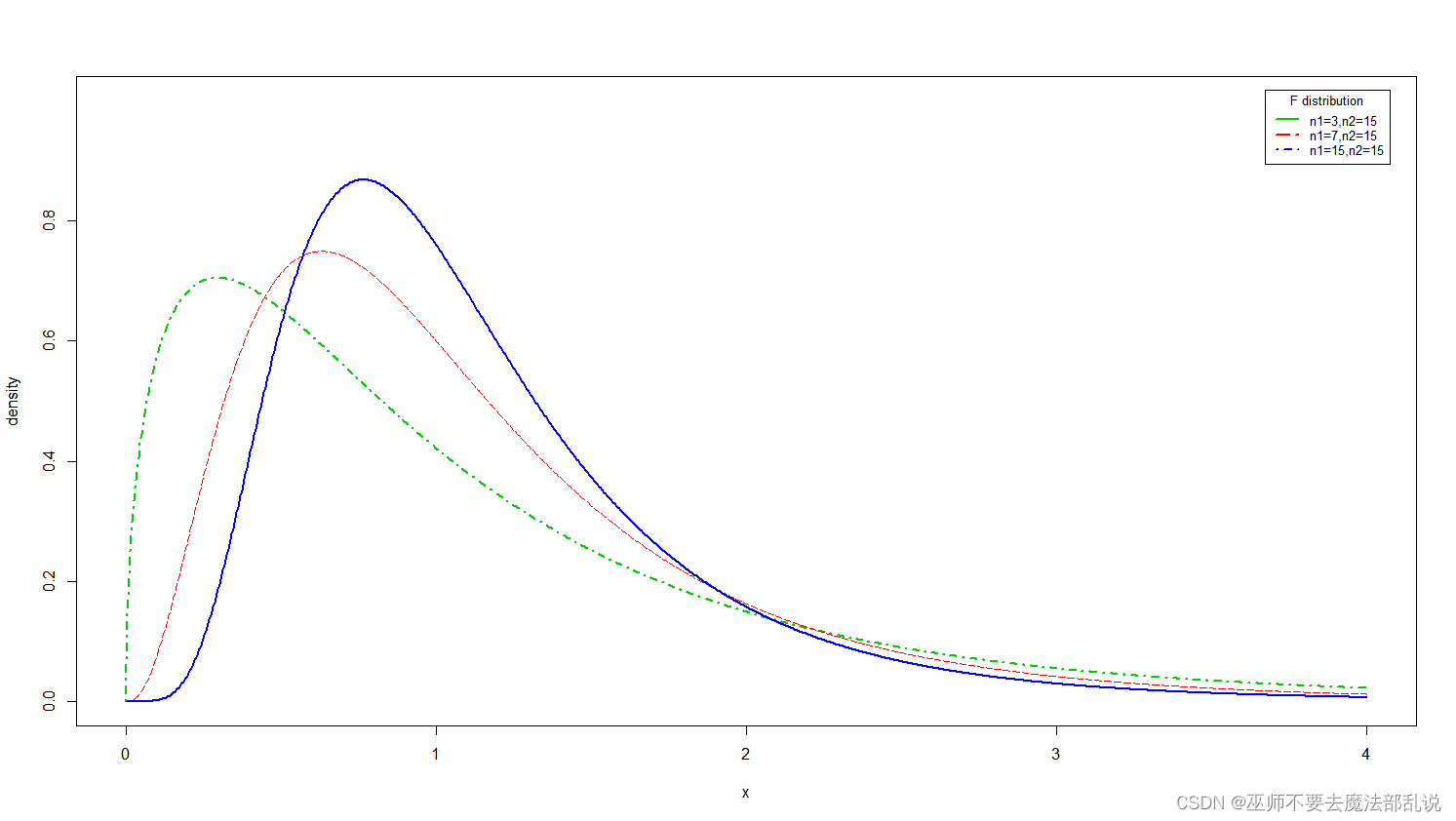
替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(0,4, length.out = 1000)y1 <- df(x,3,15)y2 <- df(x,7,15)y3 <- df(x,15,15)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 4),ylim = c(0.00, 1.0),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 4, by = 1))axis(side = 2, at = seq(0, 0.8, by = 0.2))#abline(v = 0)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "F distribution",c("n1=3,n2=15", "n1=7,n2=15","n1=15,n2=15"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("green3", "red", "blue"))思考:
常见离散型随机变量的分布有哪些?
伯努利分布、二项分布、泊松分布、几何分布、超几何分布
常见连续型随机变量的分布有哪些?
正态分布、指数分布、均匀分布、伽马分布、卡方分布、t分布、F分布
二项分布适用于__有__放回的抽样,超几何分布适用于__无__放回的抽样。(填“有”或“无”)
描述某一特定时间段内或空间段内事件发生次数的随机变量,通常服从什么分布?
泊松分布
描述两个事件间隔时间长度的随机变量,通常服从什么分布?
指数分布
统计量是样本的函数,且不包含总体的未知参数,它是随机变量吗?
统计量是随机变量
常用的抽样方法有两大类:概率型抽样方法和非概率抽样方法。它们各自又含有哪些具体的方法?
概率型抽样方法包括简单随机抽样、分层抽样、整群抽样、多阶段抽样等;
非概率抽样方法包括方便抽样、判断抽样、整齐抽样、比例抽样等。
相关文章:

R实验 随机变量及其分布
实验目的: 掌握常见几种离散性随机变量及其分布在R语言中对应的函数用法;掌握常见几种连续性随机变量及其分布在R语言中对应的函数用法;掌握统计量的定义及统计三大抽样分布在R语言中对应的函数用法。 实验内容: (习题…...

rapidssl泛域名https600元一年
泛域名https证书也可以称之为通配符https证书,指的是可以用一张https证书为多个网站(主域名以及主域名下的所有子域名网站)传输数据加密,并且提供身份认证服务的数字证书产品。RapidSSL旗下的泛域名https证书性价比高,申请速度快,…...
月薪5万是怎样谈的?
知识星球(星球名:芯片制造与封测技术社区,星球号:63559049)里的学员问:目前是晶圆厂的PE,但是想跳槽谈了几次薪水,都没法有大幅度的增长,该怎么办?“学得文武…...
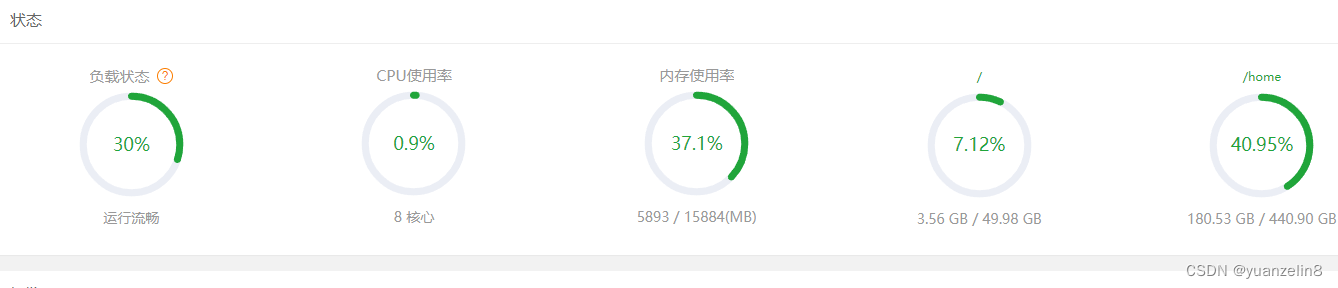
linux下宝塔负载100%解决方法
今天发现服务器宝塔面板负载居然是100% 但是cpu 和内存其实并不高 通过命令查看主机 uptime 中load average 居然高达18.23 看来负载是真的高了 通过vmstat 看看具体问题 procs: r 表示运行和等待CPU时间片的进程数,这个值如果长期大于系统CPU个数…...
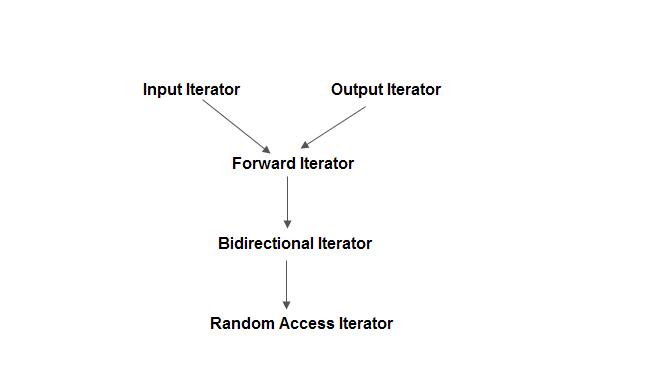
【C++】STL快速入门基础
文章目录 STL(Standard Template Library)1、一般介绍2、STL的六大组件2.1、STL容器2.2、STL迭代器2.3、相关容器的函数vectorpairstringqueuepriority_queuestackdequeset, map, multiset, multimapunordered_set, unordered_map, unordered_multiset, …...

面向对象编程的魅力与实战:以坦克飞机大战为例
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、面向对象编程的引言 二、理解面向对象编程与面向过程编程的差异 三、创建类与对象&…...

二叉树——堆的实现
一.前言 前面我们讲解了二叉树的概念以及二叉树的存储结构:https://blog.csdn.net/yiqingaa/article/details/139224974?spm1001.2014.3001.5502 今天我们主要讲讲二叉树的存储结构,以及堆的实现。 二.正文 1.二叉树的顺序结构及实现 1.1二叉树的顺序…...

【Spring】DynamicDataSourceHolder 动态数据源切换
【Spring】DynamicDataSourceHolder 动态数据源切换 常见场景常见工具一、AbstractRoutingDataSource1.1、 定义 DynamicDataSourceHolder1.2、 配置动态数据源1.3、 在Spring配置中定义数据源1.4、在业务代码中切换数据源 二、Dynamic Datasource for Spring Boot2.1. 添加依赖…...

LeeCode 3165 线段树
题意 传送门 LeeCode 3165 不包含相邻元素的子序列的最大和 题解 考虑不含相邻子序列的最大和,在不带修改的情况下容易想到,以最后一个元素是否被选取为状态进行DP。从线性递推的角度难以处理待修改的情况。 从分治的角度考虑,使用线段树…...

修改元组元素
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 场景模拟:伊米咖啡馆,由于麝香猫咖啡需求量较大,库存不足,店长想把它换成拿铁咖啡。 实例08 将麝香猫…...
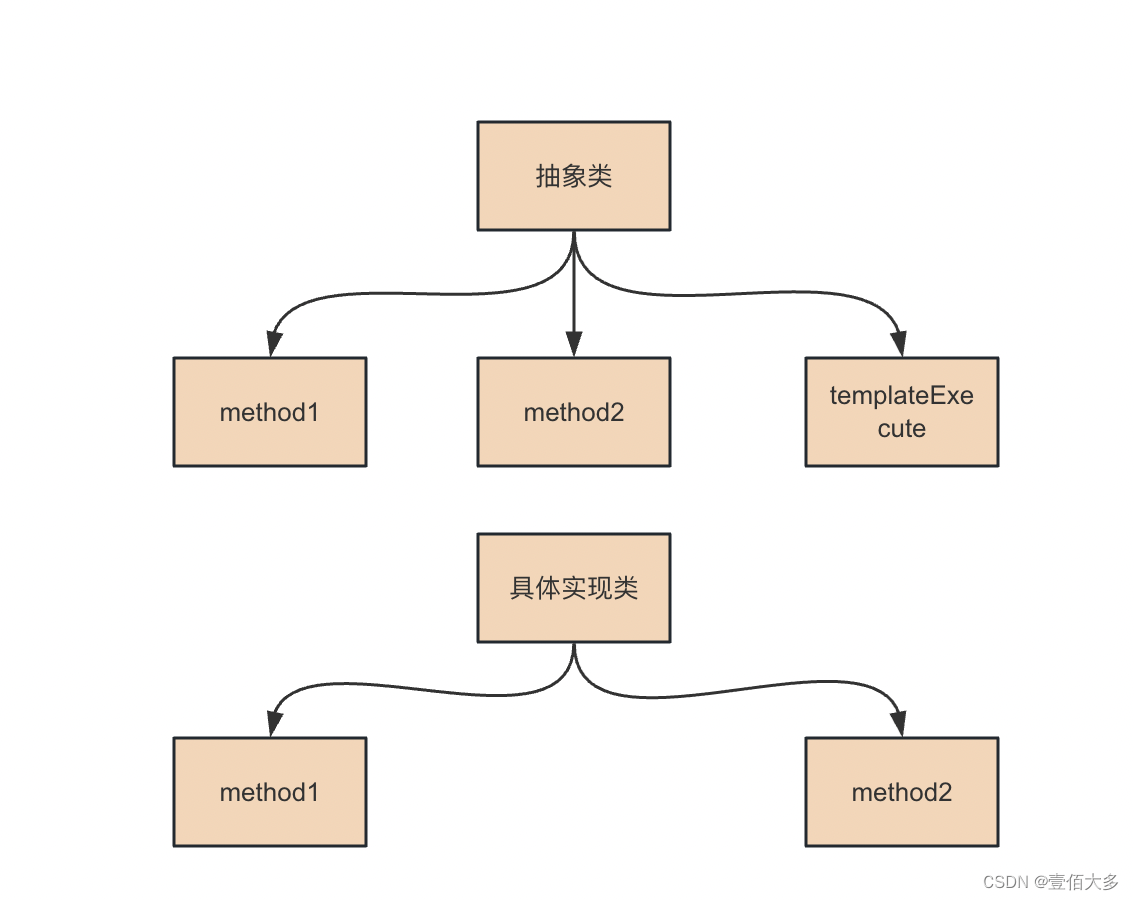
【模版方法设计模式】
文章目录 模板方法设计模式模板方法的设计原则模板方法设计模式组成部分代码实现抽象类实现具体实现类执行 模板方法设计模式 模版方法设计模式(Template Method Pattern)是一种行为设计模式,它定义了一个操作中的算法骨架,而将一…...
rust语言初识
程序设计实践课上水一篇ing 来源:rust基础入门-1.初识rust-酷程网 (kucoding.com) rust作为一名新兴语言,与go又有些许不同,因为它的目标是对标系统级开发,也就是C、C这两位在编程界的位置。比如我们最常用的windows系统&#x…...

知识图谱数据预处理笔记
知识图谱数据预处理笔记 0. 引言1. 笔记1-1. \的转义1-2. 特殊符号的清理1-3. 检查结尾是否正常1-4. 检查<>是否存在1-5. 两端空格的清理1-6. 检查object内容长时是否以<开始 0. 引言 最近学习知识图谱,发现数据有很多问题,这篇笔记记录遇到的…...
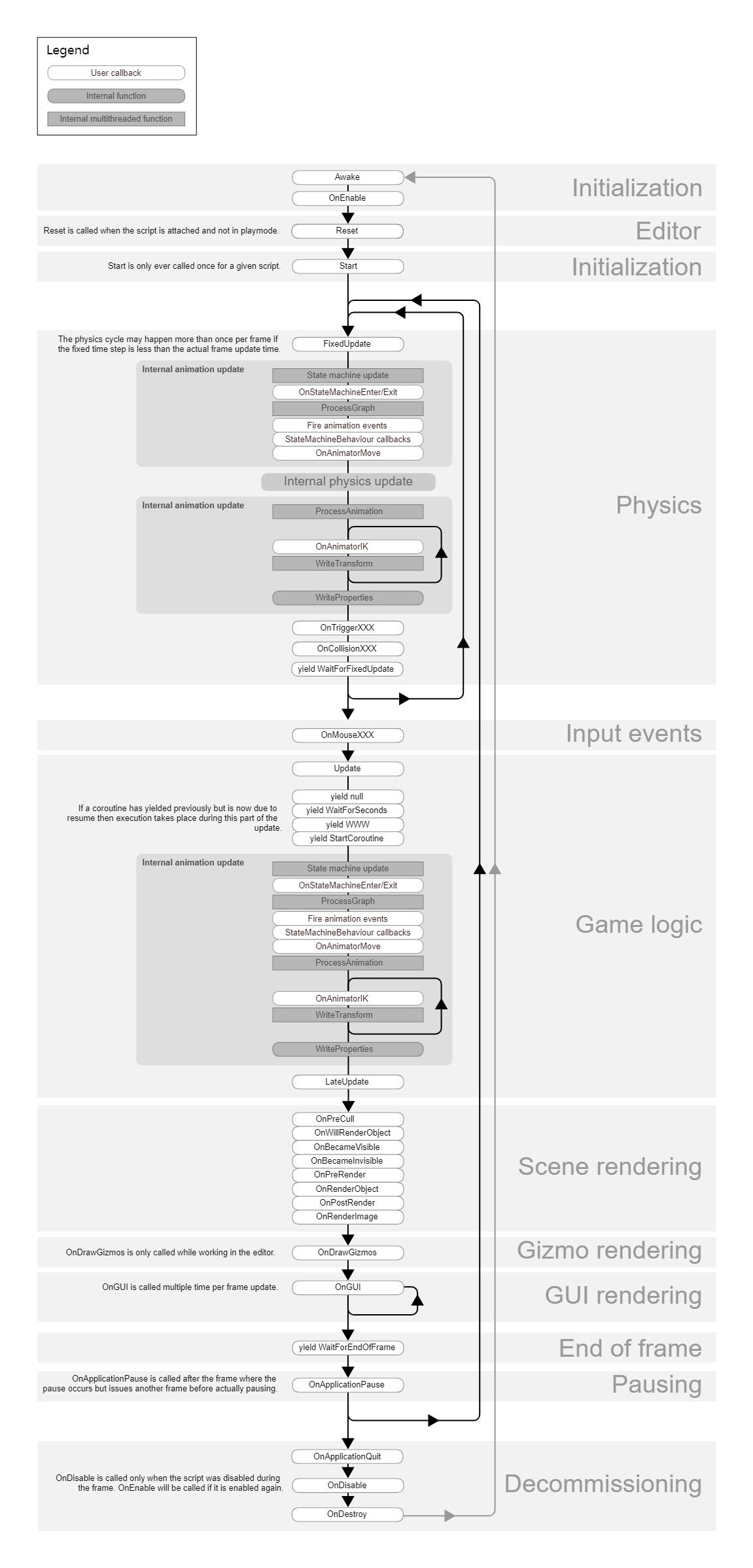
Unity面试八股文之基础篇
文章目录 前言1. Unity的生命周期加载第一个场景Editor在第一次帧更新之前帧之间更新顺序协程销毁对象时退出时 2. Unity 协程和线程,进程的区别3. 本地坐标系 世界坐标系4. 碰撞器和触发器的区别后话 前言 开设这个栏目的博文会写一些有关unity的面试题目,在面试的…...

HTTPS能否避免流量劫持?如何实现HTTPS
在当今数字化时代,网站安全已经成为企业和个人的头等大事。随着网络犯罪和数据泄露的增加,保护您的网站免受潜在威胁比以往任何时候都更加重要。网站安全的一个关键组成部分是HTTPS,它代表着安全的超文本传输协议。HTTPS是标准HTTP协议的安全…...

簡述Vue 2.0 响应式数据的原理
Vue 2.0 响应式数据的原理主要基于以下几个关键点: 数据劫持与Object.defineProperty: Vue 2.0 使用 Object.defineProperty 方法来劫持对象的属性,为其添加 getter 和 setter 方法。当数据被访问或修改时,这些 getter 和 setter …...
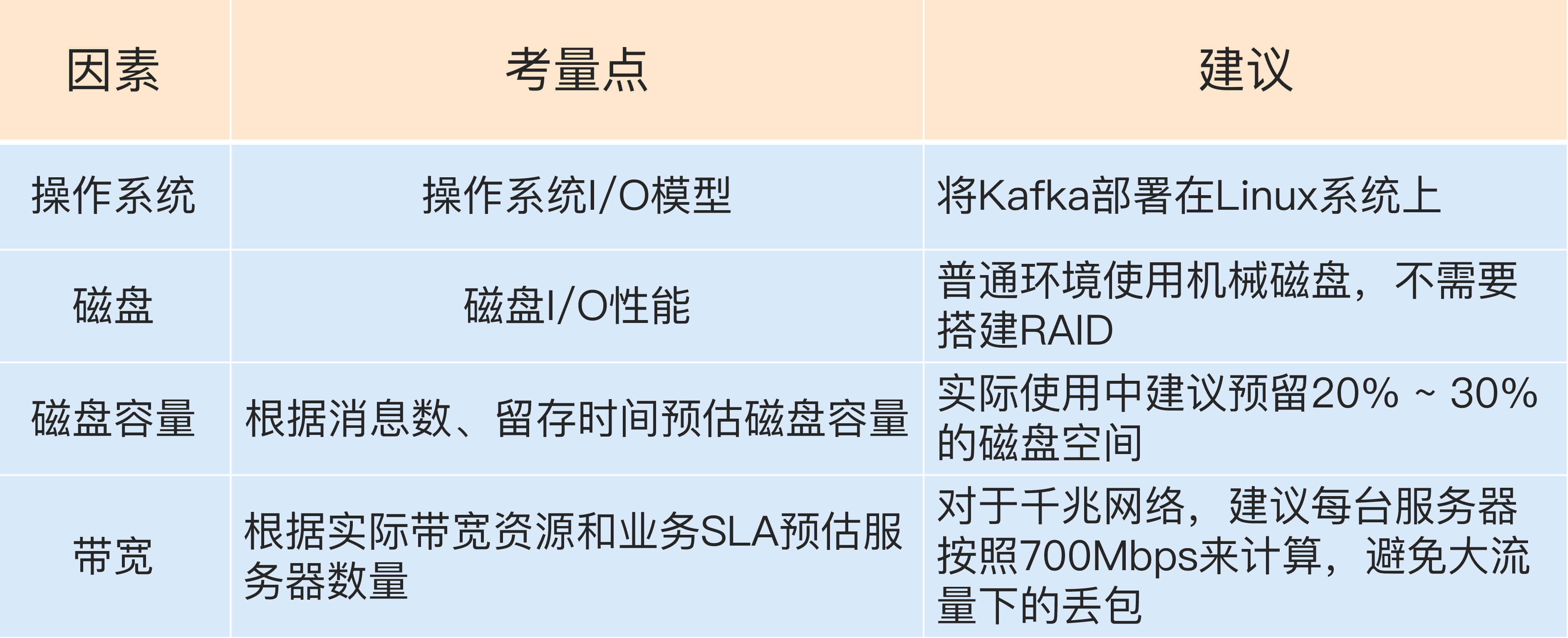
Kafka线上集群部署方案怎么做?no.6
专栏前面几期内容,我分别从Kafka的定位、版本的变迁以及功能的演进等几个方面循序渐进地梳理了Apache Kafka的发展脉络。通过这些内容,我希望你能清晰地了解Kafka是用来做什么的,以及在实际生产环境中该如何选择Kafka版本,更快地帮…...

vscode 的 AI 协助插件 Tabnine / Codeium
4.1、Tabnine 描述:Tabnine 是一款基于深度学习技术的代码自动补全工具。该插件支持多种编程语言,包括 Python、JavaScript、TypeScript、Java 和 Go 等。它可以根据您输入的代码段和上下文信息,预测并推荐可能的代码补全选项,从而…...

Flutter 中的 OutlineButton 小部件:全面指南
Flutter 中的 OutlineButton 小部件:全面指南 在Flutter的Material Design组件库中,OutlineButton是一个用于创建带边框的扁平按钮的小部件。这种按钮通常用于次要操作或在需要强调其他按钮的情况下使用。本文将为您提供一个全面的指南,帮助…...
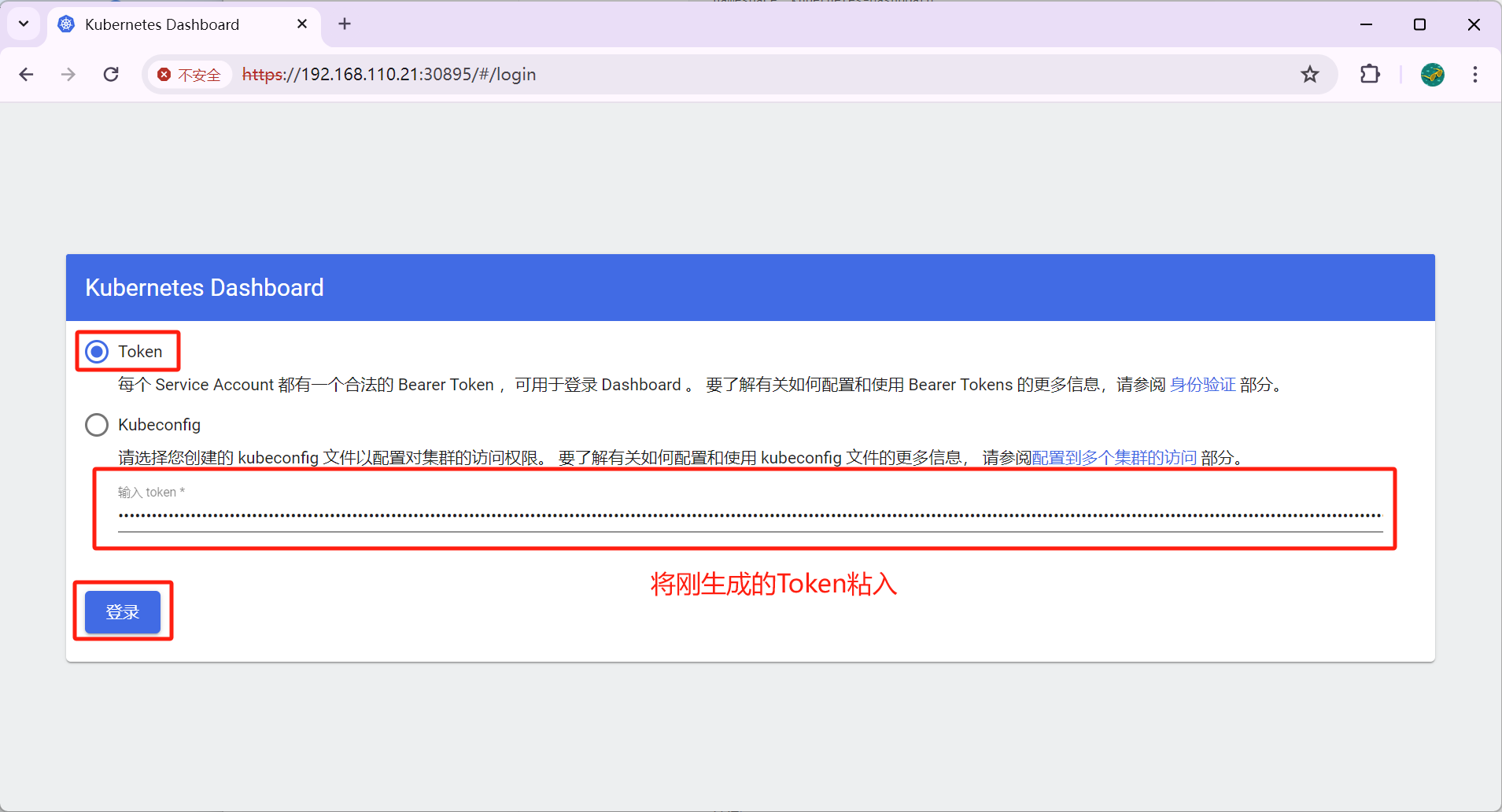
Kubernetes可视化界面之DashBoard
1.1 DashBoard Kubernetes Dashboard 是 Kubernetes 集群的一个开箱即用的 Web UI,提供了一种图形化的方式来管理和监视 Kubernetes 集群中的资源。它允许用户直接在浏览器中执行许多常见的 Kubernetes 管理任务,如部署应用、监控应用状态、执行故障排查…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
