线性化技巧:绝对值变量的线性化
文章目录
- 1. 问题
- 2. 线性化
- 3. 缺少 x i + × x i − = 0 x_i^+ \times x_i^- = 0 xi+×xi−=0 有什么问题
- 4. 延伸思考
- 5. 参考文献
1. 问题
以方述诚老师课件中的案例为例:
m a x 3 x 1 − 2 x 2 − 4 ∣ x 3 ∣ s . t . − x 1 + 2 x 2 ≤ − 5 3 x 2 − x 3 ≥ 6 2 x 1 + x 3 = 12 x 1 , x 2 ≥ 0 max \quad 3x_1-2x_2-4\vert x_3 \vert \\ s.t. -x_1+2x_2 \leq -5 \\ 3x_2-x_3 \geq 6 \\ 2x_1 + x_3 = 12 \\ x_1,x_2 \geq 0 max3x1−2x2−4∣x3∣s.t.−x1+2x2≤−53x2−x3≥62x1+x3=12x1,x2≥0
x 3 x_3 x3是一个自由变量,且在目标函数中它是以绝对值的形式存在,如果我们要将该模型转化成标准型,首先要做的就是将 x 3 x_3 x3线性化。
2. 线性化
对于每一个数字 x x x,我们都可以将它拆成正的个数 x + x^+ x+和负的个数 x − x^- x−,并将其表示为 x + − x − x^+ - x^- x+−x−(正的个数 - 负的个数),举个例子:
- 5:正的个数是5,负的个数是0,5-0=5;
- -5:正的个数是0,负的个数是5,0-5=-5。
直觉上十分合理对吧(intuition是方老师第一节课反复强调的重点),我们用数学表达式来表达上述思想。
x i ∈ R x_i \in R xi∈R
x i + = { x i , i f x i ≥ 0 0 , o t h e r w i s e x_i^+ = \begin{cases} x_i, \quad if \quad x_i \geq 0 \\ 0, otherwise \end{cases} xi+={xi,ifxi≥00,otherwise
x i − = { 0 , i f x i ≥ 0 − x i , o t h e r w i s e x_i^- = \begin{cases} 0, \quad if \quad x_i \geq 0 \\ -x_i, otherwise \end{cases} xi−={0,ifxi≥0−xi,otherwise
x i = x i + − x i − x_i = x_i^+ - x_i^- xi=xi+−xi−
x i + × x i − = 0 x_i^+ \times x_i^- = 0 xi+×xi−=0
(很多教材和文章里直接省去了这个约束,其实是不对的,待会儿后面讲。)
x i + , x i − ≥ 0 x_i^+, x_i^- \geq 0 xi+,xi−≥0
3. 缺少 x i + × x i − = 0 x_i^+ \times x_i^- = 0 xi+×xi−=0 有什么问题
x i + × x i − = 0 x_i^+ \times x_i^- = 0 xi+×xi−=0 该约束本质保证的是 x i + x_i^+ xi+ 和 x i − x_i^- xi− 至少有一个为0,如果没有该约束,5除了表示为5-0以外,还可以表示为6-1、7-2等等。也就是会使得原来只有一个解的问题,变成具有很多个新的解的问题。
4. 延伸思考
上述问题中的 ∣ x ∣ \vert x \vert ∣x∣是一个“V”字型的凸函数,它可以求极小值。如果要求 m a x ∣ x ∣ max \vert x \vert max∣x∣ 那就unbounded了。
5. 参考文献
- Linear Programming
相关文章:

线性化技巧:绝对值变量的线性化
文章目录 1. 问题2. 线性化3. 缺少 x i x i − 0 x_i^ \times x_i^- 0 xixi−0 有什么问题4. 延伸思考5. 参考文献 1. 问题 以方述诚老师课件中的案例为例: m a x 3 x 1 − 2 x 2 − 4 ∣ x 3 ∣ s . t . − x 1 2 x 2 ≤ − 5 3 x 2 − x 3 ≥ 6 2 x 1 …...

List基本使用(C++)
目录 1.list的介绍 2.list的使用 list的构造 list的size() 和 max_size() list遍历操作 list元素修改操作 assign()函数 push_front(),push_back 头插,尾插 pop_front() pop_back 头删尾删 insert()函数 swap()函数 resize()函数 clear()函数 list类数…...

ELK 日志监控平台(一)- 快速搭建
文章目录 ELK 日志监控平台(一)- 快速搭建1.ELK 简介2.Elasticsearch安装部署3.Logstash安装部署4.Kibana安装部署5.日志收集DEMO5.1.创建SpringBoot应用依赖导入日志配置文件 logback.xml启动类目录结构启动项目 5.2.创建Logstash配置文件5.3.重新启动L…...

工作中写单片机代码,与学校里有什么不同?
来聊聊我的经历,提供几个提升方向,亲测有效,希望能让你少走几年弯路。 10几年前,还没参加工作的时候,主要是玩玩开发板,也接触不到实际产品的代码,很好奇那些产品级的代码是怎样的。 第一份工作…...
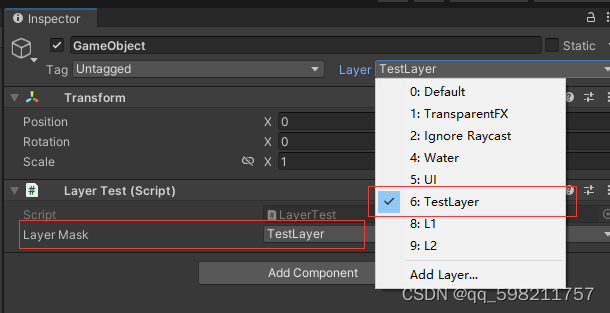
Unity LayerMask避坑笔记
今天使用Physics2D.OverlapAreaNonAlloc进行物理检测时候,通过LayerMask.NameToLayer传入了int值的LayerMask,结果一直识别不到,经过Debug才找到问题,竟是LayerMask的“值”传输有问题,记录一下。 直接贴代码输出结果&…...

(原创)从右到左排列RecycleView的数据
问题的提出 当我们写一个Recycleview时,默认的效果大概是这样的: 当然,我们也可以用表格布局管理器GridLayoutManager做成这样: 可以看到,默认的绘制方向是: 从左到右,从上到下 那么问题来了…...
【C语言】数据指针地址的取值、赋值、自增操作避坑
【C语言】数据指针的取值、赋值、自增操作避坑 文章目录 指针地址指针自增指针取值、赋值附录:压缩字符串、大小端格式转换压缩字符串浮点数压缩Packed-ASCII字符串 大小端转换什么是大端和小端数据传输中的大小端总结大小端转换函数 指针地址 请看下列代码&#…...

Java进阶-SpringCloud使用BeanUtil工具类简化对象之间的属性复制和操作
在Java编程中,BeanUtil工具类是一种强大且便捷的工具,用于简化对象之间的属性复制和操作。本文将介绍BeanUtil的基本功能,通过详细的代码示例展示其应用,并与其他类似工具进行对比。本文还将探讨BeanUtil在实际开发中的优势和使用…...

【ES6】ECMAS6新特性概览(一):变量声明let与const、箭头函数、模板字面量全面解析
🔥 个人主页:空白诗 🔥 热门专栏:【JavaScript】 文章目录 🌿 引言一、 let 和 const - 变量声明的新方式 🌟📌 var的问题回顾📌 let的革新📌 const的不变之美 二、 Arro…...
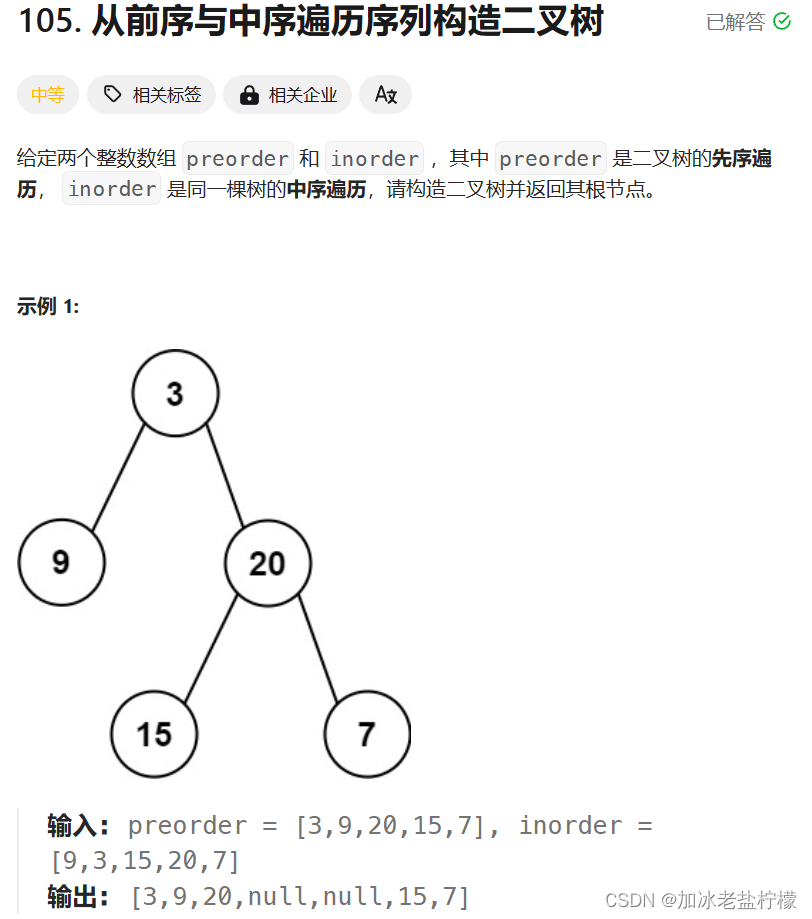
刷题之从前序遍历与中序遍历序列构造二叉树(leetcode)
从前序遍历与中序遍历序列构造二叉树 前序遍历:中左右 中序遍历:左中右 前序遍历的第一个数必定为根节点,再到中序遍历中找到该数,数的左边是左子树,右边是右子树,进行递归即可。 #include<vector>…...
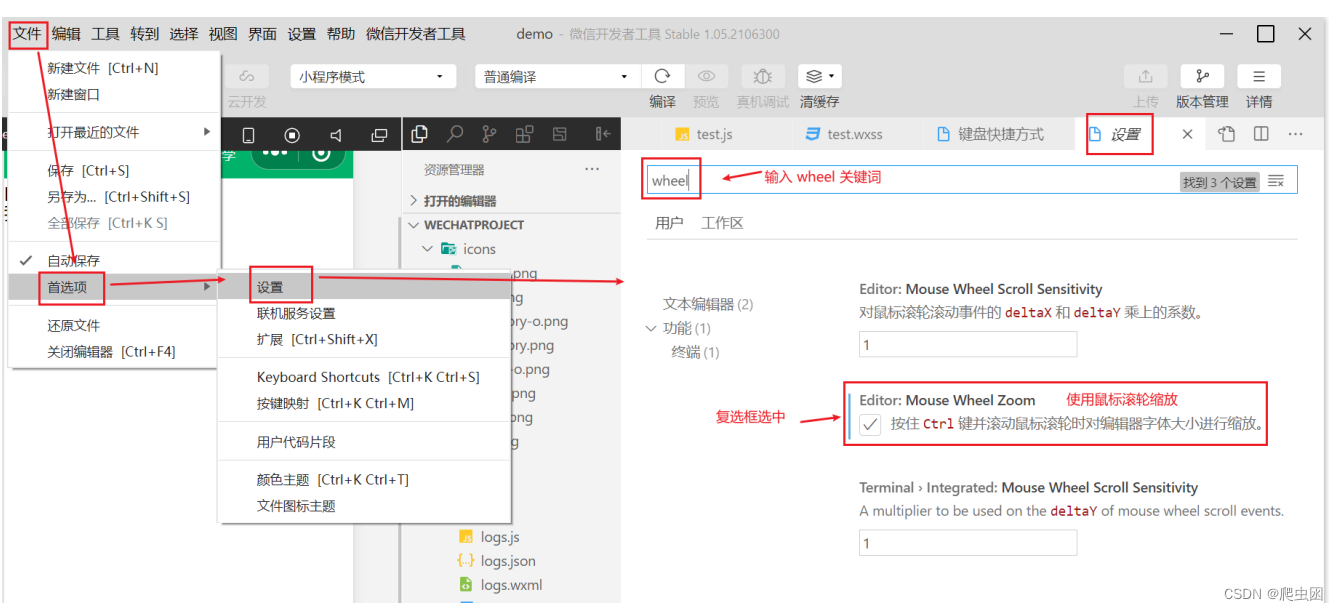
微信小程序--微信开发者工具使用小技巧(3)
一、微信开发者工具使用小技巧 1、快速创建小程序页面 在app.json中的pages配置项,把需要创建的页面填写上去 2、快捷键使用 进入方式 1: 文件–>首选项–> keyboard shortcuts 进入快捷键查看与设置 进入方式 2: 设置–>快捷键…...

JDBC的 PreparedStatement 的用法和解释
文章目录 前言1、封装数据库连接和关闭操作数据库配置文件 config.properties 2、批量添加操作3、查询操作4、修改和删除操作总结 前言 PreparedStatement是预编译的,对于批量处理可以大大提高效率. 也叫JDBC存储过程 1、封装数据库连接和关闭操作 package org.springblade.m…...

LeetCode 面试150
最近准备面试,我以前不愿意面对的 现在保持一颗本心,就是专注于算法思想,语言基础的磨炼; 不为速成,不急功近利的想要比赛,或者为了面试。 单纯的本心,体验算法带来的快乐,是一件非常…...

xmake+xrepo自建仓库添加交叉编译工具链
xmakexrepo自建仓库添加交叉编译工具链 最近想将交叉编译工具链放到xrepo自建仓库中,在xmake中引用,方便多个电脑快速实现交叉编译。 xmake官方文档感觉不够详细,折腾了好久,这里做个记录。 基本步骤如下: 添加自建…...

论文阅读》学习了解自己:一个粗略到精细的个性化对话生成的人物感知训练框架 AAAI 2023
《论文阅读》学习了解自己:一个粗略到精细的个性化对话生成的人物感知训练框架 AAAI 2023 前言 简介研究现状任务定义模型架构Learning to know myselfLearning to avoid Misidentification损失函数实验结果消融实验 前言 亲身阅读感受分享,细节画图解释…...

[Java EE] 网络编程与通信原理(三):网络编程Socket套接字(TCP协议)
🌸个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 🏵️热门专栏:🍕 Collection与数据结构 (92平均质量分)https://blog.csdn.net/2301_80050796/category_12621348.html?spm1001.2014.3001.5482 🧀Java …...
)
MyBatis懒加载数据(大批量数据处理)
使用范例 Cursor约定使用Iterator去懒加载数据,以时间换空间,非常适合处理通常无法容纳在内存中的数百万个项目查询。如果在 resultMap 中使用集合,则必须使用 resultMap 的 id 列对游标 SQL 查询进行排序(resultOrdered“true”)。 //为了避…...

MySQL--联合索引应用细节应用规范
目录 一、索引覆盖 1.完全覆盖 2.部分覆盖 3.不覆盖索引-where条件不包含联合索引的最左则不覆盖 二、MySQL8.0在索引中的新特性 1.不可见索引 2.倒序索引 三、索引自优化--索引的索引 四、Change Buffer 五、优化器算法 1.查询优化器算法 2.设置算法 3.索引下推 …...
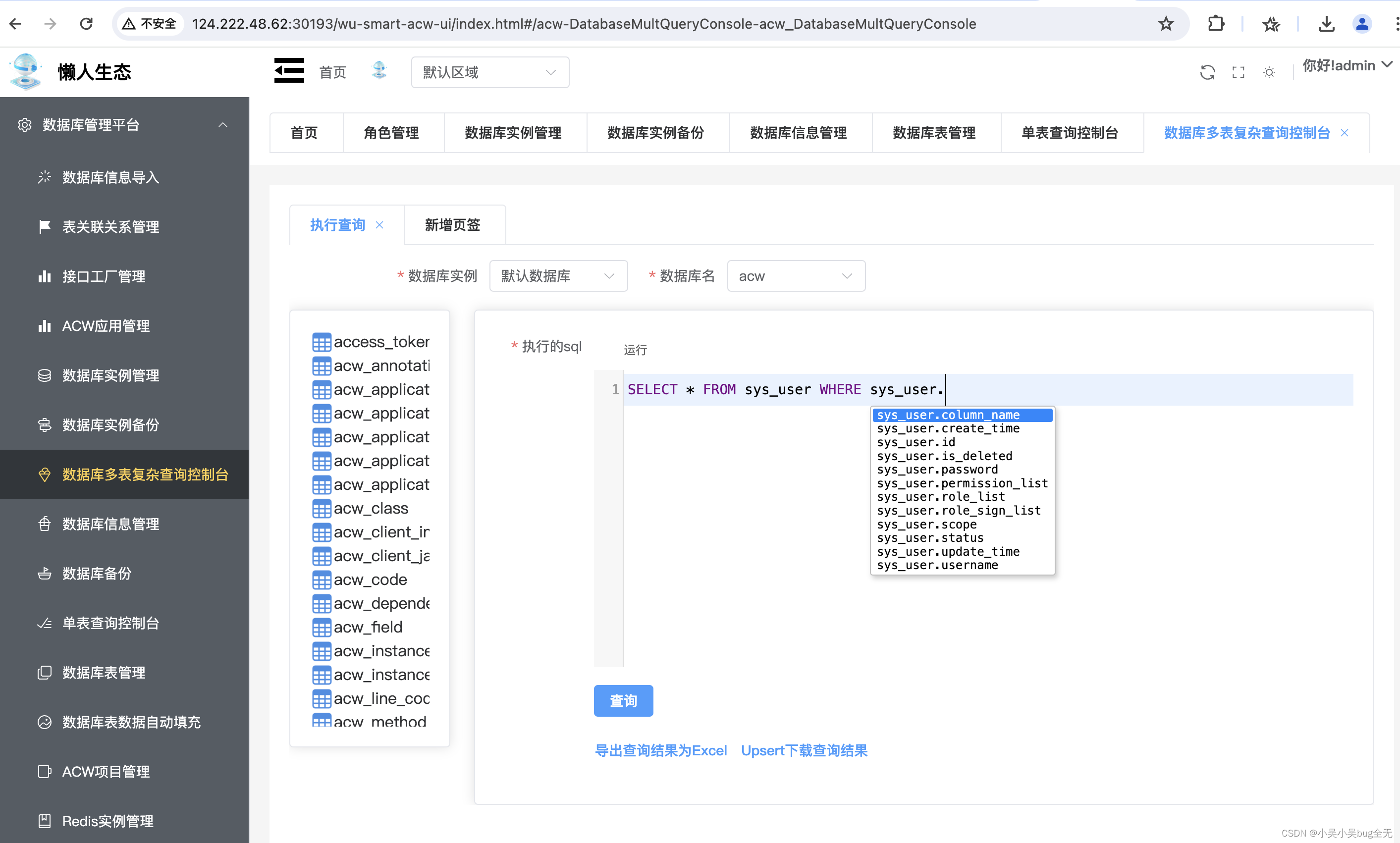
【spring boot+Lazy ORM+mysql】开发一个数据库管理系统实现对应数据库数据查看和修改
【spring bootLazy ORMmysql】开发一个数据库管理系统实现对应数据库数据查看和修改 演示项目地址:http://124.222.48.62:30193/wu-smart-acw-ui/index.html#/login (admin/admin) 功能 用户登录注册新增、编辑数实例新增、编辑数据库信息…...
知识分享:隔多久查询一次网贷大数据信用报告比较好?
随着互联网金融的快速发展,越来越多的人开始接触和使用网络贷款。而在这个过程中,网贷大数据信用报告成为了评估借款人信用状况的重要依据。那么,隔多久查询一次网贷大数据信用报告比较好呢?接下来随小易大数据平台小编去看看吧。 首先&…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

Qt/C++学习系列之列表使用记录
Qt/C学习系列之列表使用记录 前言列表的初始化界面初始化设置名称获取简单设置 单元格存储总结 前言 列表的使用主要基于QTableWidget控件,同步使用QTableWidgetItem进行单元格的设置,最后可以使用QAxObject进行单元格的数据读出将数据进行存储。接下来…...
【Docker 02】Docker 安装
🌈 一、各版本的平台支持情况 ⭐ 1. Server 版本 Server 版本的 Docker 就只有个命令行,没有界面。 Platformx86_64 / amd64arm64 / aarch64arm(32 - bit)s390xCentOs√√Debian√√√Fedora√√Raspbian√RHEL√SLES√Ubuntu√√√√Binaries√√√ …...

【优选算法】模拟 问题算法
一:替换所有的问号 class Solution { public:string modifyString(string s) {int n s.size();for(int i 0; i < n; i){if(s[i] ?){for(char ch a; ch < z; ch){if((i0 && ch !s[i1]) || (in-1 && ch ! s[i-1]) || ( i>0 &&…...
