C语言例题46、根据公式π/4=1-1/3+1/5-1/7+1/9-1/11+…,计算π的近似值,当最后一项的绝对值小于0.000001为止
#include <stdio.h>
#include <math.h>int main() {int fm = 1;//分母double sign = 1;//正负号double fzs = 1;//分子式double sum = 0;while (fabs(fzs) >= 0.000001) {sum += fzs;sign *= -1; //变换正负号fm += 2; //分母3、5、7、9...增长fzs = sign / fm;//分子式}printf("π的近似值为%.5lf\n", sum * 4);
}
运行结果:

本章C语言经典例题合集:http://t.csdnimg.cn/FK0Qg
相关文章:

C语言例题46、根据公式π/4=1-1/3+1/5-1/7+1/9-1/11+…,计算π的近似值,当最后一项的绝对值小于0.000001为止
#include <stdio.h> #include <math.h>int main() {int fm 1;//分母double sign 1;//正负号double fzs 1;//分子式double sum 0;while (fabs(fzs) > 0.000001) {sum fzs;sign * -1; //变换正负号fm 2; //分母3、5、7、9...增长fzs sign / fm;//分子式…...
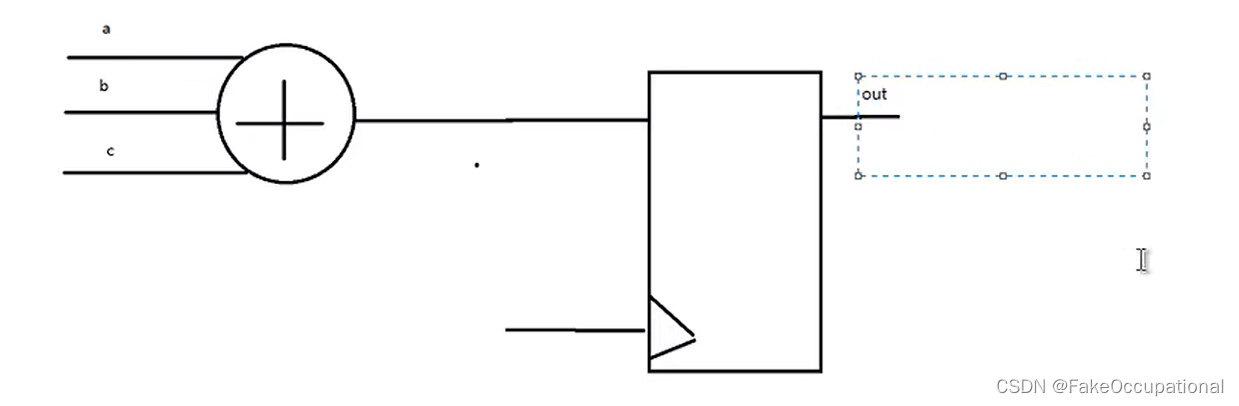
fpga系列 HDL: 05 阻塞赋值(=)与非阻塞赋值(<=)
在Verilog硬件描述语言(HDL)中,信号的赋值方式主要分为两种:连续赋值和过程赋值。每种赋值方式有其独特的用途和语法,并适用于不同类型的电路描述。 1. 连续赋值(Continuous Assignment,assign 和…...
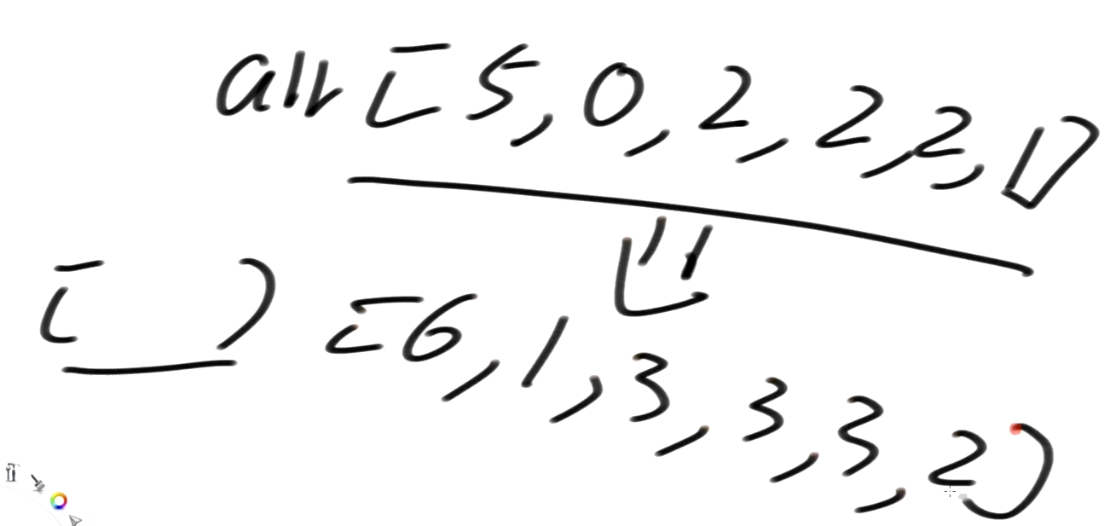
大白话DC3算法
DC3算法是什么 DC3算法(也称为Skew算法)是一种高效的构建后缀数组的算法,全称为Difference Cover Modulo 3算法。 该算法于2002年被提出,论文参考: https://www.cs.cmu.edu/~guyb/paralg/papers/KarkkainenSanders0…...

力扣HOT100 - 75. 颜色分类
解题思路: 单指针,对数组进行两次遍历。 class Solution {public void sortColors(int[] nums) {int p 0;int n nums.length;for (int i 0; i < n; i) {if (nums[i] 0) {int tmp nums[i];nums[i] nums[p];nums[p] tmp;p;}}for (int i p; i …...

Vue.js - 计算属性与侦听器 【0基础向 Vue 基础学习】
文章目录 计算属性 computedcomputed 的使用方法computed 与 method 的区别计算属性完整写法 watch 侦听器(监视器)简单写法 → 简单类型数据,直接监视完整写法 → 添加额外配置项 计算属性 computed computed 的使用方法 **概念࿱…...

技术速递|使用 C# 集合表达式重构代码
作者:David Pine 排版:Alan Wang 本文是系列文章的第二篇,该系列文章涵盖了探索 C# 12功能的各种重构场景。在这篇文章中,我们将了解如何使用集合表达式重构代码,我们将学习集合初始化器、各种表达式用法、支持的集合目…...
我的世界开服保姆级教程
前言 Minecraft开服教程 如果你要和朋友联机时,可以选择的方法有这样几种: 局域网联机:优点:简单方便,在MC客户端里自带。缺点:必须在同一局域网内。 有些工具会带有联机功能:优点:一…...
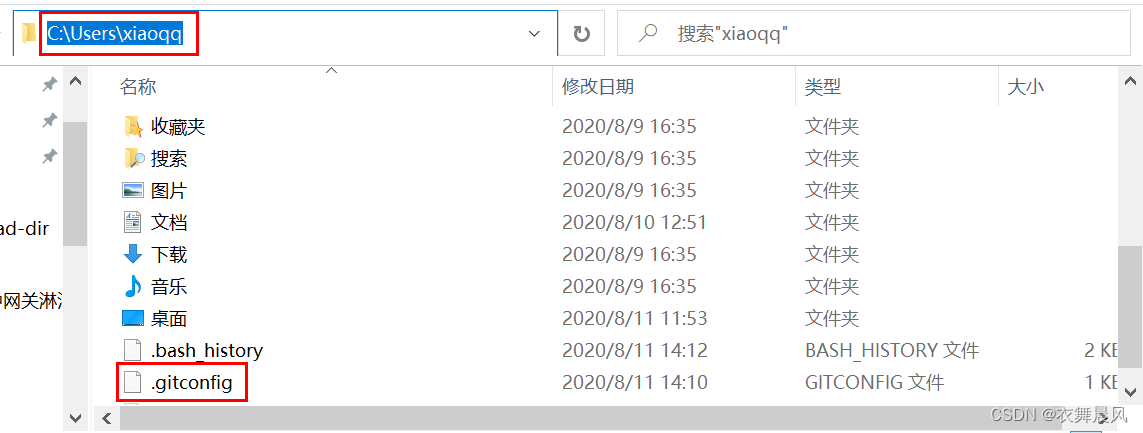
[转载]同一台电脑同时使用GitHub和GitLab
原文地址:https://developer.aliyun.com/article/893801 简介: 工作中我们有时可能会在同一台电脑上使用多个git账号,例如:公司的gitLab账号,个人的gitHub账号。怎样才能在使用gitlab与github时,切换成对应…...

【网络协议】【OSI】一次HTTP请求OSI工作过程详细解析
目录 1. 一次HTTP请求OSI工作过程 1.1 应用层(第7层) 1.2 表示层(第6层) 1.3 会话层(第5层) 1.4 传输层(第4层)...

springboot vue 开源 会员收银系统 (2) 搭建基础框架
前言 完整版演示 前面我们对会员系统https://blog.csdn.net/qq_35238367/article/details/126174288进行了分析 确定了技术选型 和基本的模块 下面我们将从 springboot脚手架开发一套收银系统 使用脚手架的好处 不用编写基础的rabc权限系统将工作量回归业务本身生成代码 便于…...

Java进阶学习笔记26——包装类
包装类: 包装类就是把基本类型的数据包装成对象。 看下API文档: deprecated:极力反对、不赞成的意思。 marked for removal:标识为去除的意思。 自动装箱:基本数据类型可以自动转换成包装类。 自动拆箱:…...

【JavaEE进阶】——要想代码不写死,必须得有spring配置(properties和yml配置文件)
目录 本章目标: 🚩配置文件 🚩SpringBoot配置文件 🎈配置⽂件的格式 🎈 properties 配置⽂件说明 📝properties语法格式 📝读取配置文件 📝properties 缺点分析 dz…...

第十四 Elasticsearch介绍和安装
docker-compose安装 kibana: image: docker.elastic.co/kibana/kibana:7.5.1 container_name: kibana ports: - "5601:5601" environment: ELASTICSEARCH_HOSTS: http://elasticsearch:9200 depends_on: - elasticsearch…...
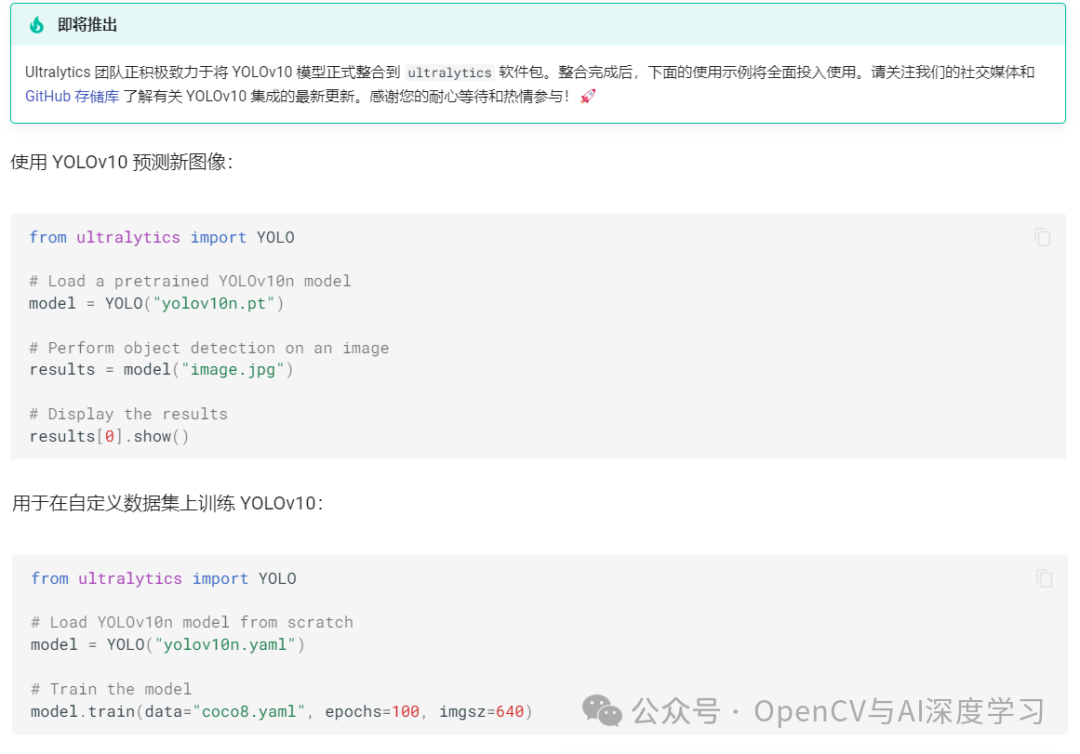
YOLOv10介绍与推理--图片和视频演示(附源码)
导 读 本文主要对YOLOv10做简单介绍并给出推理图片和视频的步骤演示。 YOLOv10简介 YOLOv10是清华大学的研究人员在Ultralytics Python包的基础上,引入了一种新的实时目标检测方法,解决了YOLO 以前版本在后处理和模型架构方面的不足。通过消除非最大抑…...

Java实验08
实验一 demo.java package q8.demo02;public class demo{public static void main(String[] args) {WindowMenu win new WindowMenu("Hello World",20,30,600,290);} }WindowMenu.java package q8.demo02; import javax.swing.*;public class WindowMenu extends…...
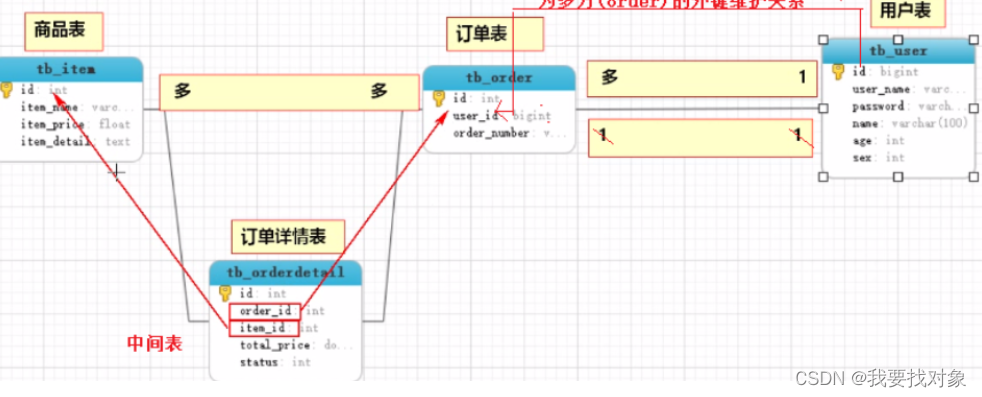
MyBatis复习笔记
3.Mybatis复习 3.1 xml配置 properties:加载配置文件 settings:设置驼峰映射 <settings><setting name"mapUnderscoreToCamelCase" value"true"/> </settings>typeAliases:类型别名设置 #这样在映射…...

HTML的基石:区块标签与小语义标签的深度解析
📚 HTML的基石:区块标签与小语义标签的深度解析 🌐 区块标签:构建网页的框架🏠 <div>:万能的容器📚 <section>、<article>、<aside>:语义化的布局 …...

Windows域控简介
一、Windows 域控概念 Windows 域控即 Active Directory(AD)域控制器,它是 Windows Server 中的一个角色,用于管理网络中的用户帐户、计算机和其他设备。AD 域控制器的功能包括: 用户认证:允许用户通过用…...

项目延期,不要随意加派人手
遇到软件项目出现延期的情况时,不建议随意加派人手。原因如下: 有些任务是不可拆分的,不能拆分为多个并行任务,增加人员不会加快项目进度。新增加人员需要原有人员介绍项目中的技术架构、业务知识,在开发过程中也难免…...
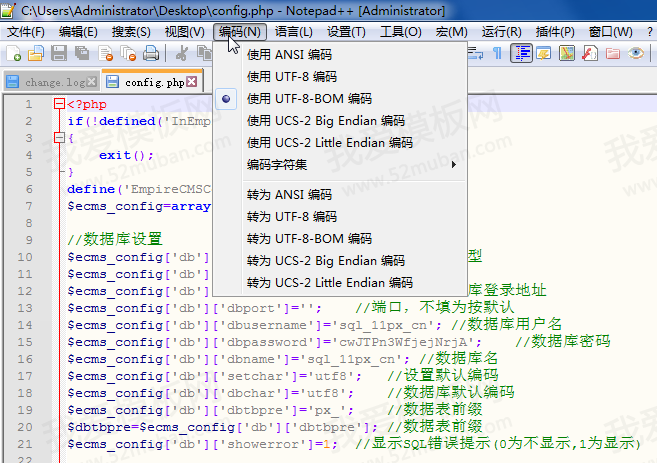
帝国CMS验证码不显示怎么回事呢?
帝国CMS验证码有时候会不显示或打叉,总结自己的解决方法。 1、检查服务器是否开启GD库 测试GD库是否开启的方法:浏览器访问:/e/showkey/index.php,如果出现一堆乱码或报错,证明GD库没有开启,开启即可。 2…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
