【CTF Web】CTFShow web3 Writeup(SQL注入+PHP+UNION注入)
web3
1
管理员被狠狠的教育了,所以决定好好修复一番。这次没问题了。
解法

注意到:
<!-- flag in id = 1000 -->
但是拦截很多种字符。
if(preg_match("/or|\-|\\|\*|\<|\>|\!|x|hex|\+/i",$id)){die("id error");
}
使用UNION注入:
?id=1 and 1=0 union select * from article where id=1000
取得 flag。

Flag
ctfshow{2dc7e880-3e21-4599-9c2b-c9b4a8009889}
声明
本博客上发布的所有关于网络攻防技术的文章,仅用于教育和研究目的。所有涉及到的实验操作都在虚拟机或者专门设计的靶机上进行,并且严格遵守了相关法律法规。
博主坚决反对任何形式的非法黑客行为,包括但不限于未经授权的访问、攻击或破坏他人的计算机系统。博主强烈建议每位读者在学习网络攻防技术时,必须遵守法律法规,不得用于任何非法目的。对于因使用这些技术而导致的任何后果,博主不承担任何责任。
相关文章:

【CTF Web】CTFShow web3 Writeup(SQL注入+PHP+UNION注入)
web3 1 管理员被狠狠的教育了,所以决定好好修复一番。这次没问题了。 解法 注意到: <!-- flag in id 1000 -->但是拦截很多种字符。 if(preg_match("/or|\-|\\|\*|\<|\>|\!|x|hex|\/i",$id)){die("id error"); }使用…...
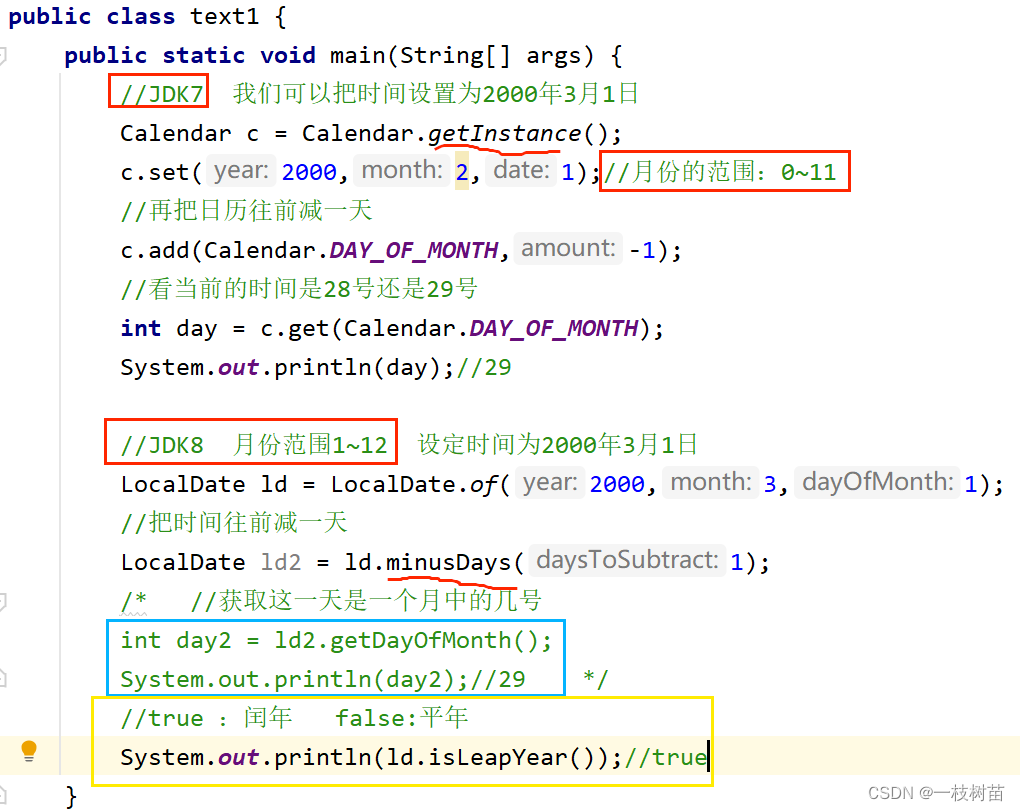
常见API(JDK7时间、JDK8时间、包装类、综合练习)
一、JDK7时间——Date 1、事件相关知识点 2、Date时间类 Data类是一个JDK写好的Javabean类,用来描述时间,精确到毫秒。 利用空参构造创建的对象,默认表示系统当前时间。 利用有参构造创建的对象,表示指定的时间。 练习——时间计…...
)
Docker数据卷(volume)
数据卷 数据卷是一个虚拟目录,是容器内目录与宿主机目录之间映射的桥梁。(容器内目录与宿主机目录对应的桥梁,修改宿主机对应的目录,docker会映射到容器内部,相当于修改了容器内的,反之也一样)数…...

30.哀家要长脑子了!---栈与队列
1.388. 文件的最长绝对路径 - 力扣(LeetCode) 其实看懂了就还好 用一个栈来保存所遍历过最大的文件的绝对路径的长度,栈顶元素是文件的长度,栈中元素的个数是该文件目录的深度,非栈顶元素就是当时目录的长度 检查此…...
多重继承引起的二义性问题和虚基类
多重继承容易引起的问题就是因为继承的成员同名而产生的二义性问题。 例:类A和类B中都有成员函数display和数据成员a,类C是类A和类B的直接派生类 情况一: class A {public:int a;void display(); }; class B {public:int a;void display; }; class C:…...

ciscn
ciscn Crypto部分复现 古典密码 先是埃特巴什密码(这个需要进行多次测试),然后base64,再栅栏即可 答案:flag{b2bb0873-8cae-4977-a6de-0e298f0744c3} _hash 题目: #!/usr/bin/python2 # Python 2.7 (6…...
智能的PHP开发工具PhpStorm v2024.1全新发布——支持PHPUnit 11.0
PhpStorm是一个轻量级且便捷的PHP IDE,其旨在提高用户效率,可深刻理解用户的编码,提供智能代码补全,快速导航以及即时错误检查。可随时帮助用户对其编码进行调整,运行单元测试或者提供可视化debug功能。 立即获取PhpS…...
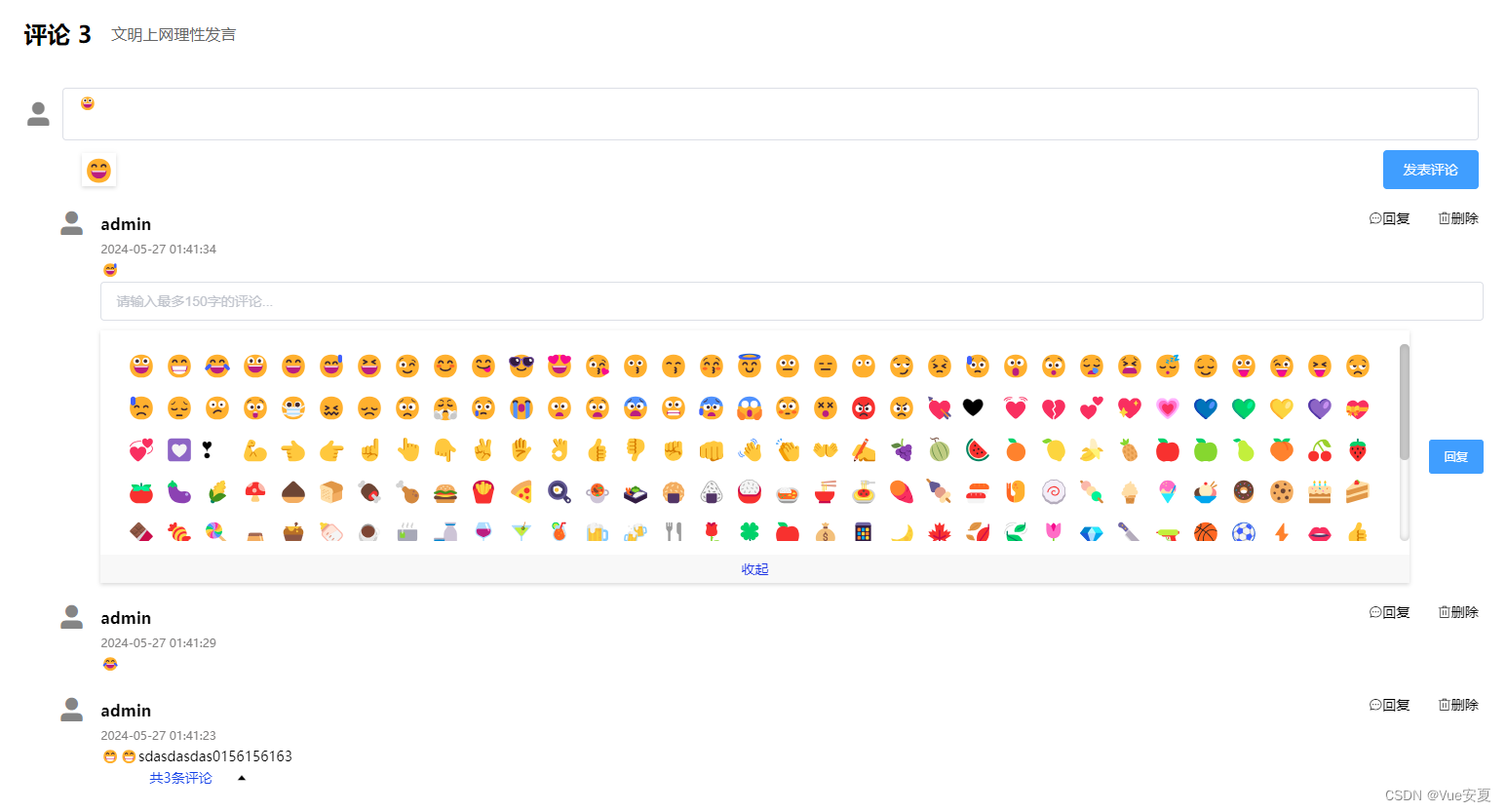
Vue2+Element 封装评论+表情功能
有需要的小伙伴直接拿代码即可,不需要下载依赖,目前是初始版本,后期会进行代码的优化。 评论组件如下: 创建 comment.vue 文件。 表情组件 VueEmoji.vue 在评论组件中使用。 <template><div class"comment"…...

【k8s】存储 pvc 参数列表
相关文章: 【K8s】初识PV和PVC 【k8s】存储 pv 参数列表 【k8s】存储 pvc 参数列表 1. pv概述 2. 参数列表 [rootpaas-controller-3:/home/ubuntu]$ kubectl explain pvc.spec KIND: PersistentVolumeClaim VERSION: v1RESOURCE: spec <Object>DESCRI…...

数据集007:垃圾分类数据集(含数据集下载链接)
数据集简介 本数据拥有 训练集:43685张; 验证集:5363张; 测试集:5363张; 总类别数:158类。 部分代码: 定义数据集 class MyDataset(Dataset):def __init__(self, modetrain, …...
Spring常用注解(超全面)
官网:核心技术SPRINGDOC.CN 提供 Spring 官方文档的翻译服务,可以方便您快速阅读中文版官方文档。https://springdoc.cn/spring/core.html#beans-standard-annotations 1,包扫描组件标注注解 Component:泛指各种组件 Controller、…...

HQL面试题练习 —— 合并活动日期
目录 1 题目2 建表语句3 题解 1 题目 已知有表记录了每个大厅的活动开始日期和结束日期,每个大厅可以有多个活动。请编写一个SQL查询合并在同一个大厅举行的所有重叠的活动,如果两个活动至少有一天相同,那他们就是重叠的,请将他们…...

基于SVm和随机森林算法模型的中国黄金价格预测分析与研究
摘要 本研究基于回归模型,运用支持向量机(SVM)、决策树和随机森林算法,对中国黄金价格进行预测分析。通过历史黄金价格数据的分析和特征工程,建立了相应的预测模型,并利用SVM、决策树和随机森林算法进行训…...

Host头攻击-使用反向代理服务器或负载均衡器来传递路由信息
反向代理服务器的作用 安全性:反向代理服务器位于Web服务器之前,可以隐藏实际Web服务器的身份和地址,从而增加安全性。它还可以对客户端请求进行过滤和检查,以防止潜在的攻击。负载均衡:反向代理服务器可以将客户端请…...

AWS容器之Amazon ECS
Amazon Elastic Container Service(Amazon ECS)是亚马逊提供的一种完全托管的容器编排服务,用于在云中运行、扩展和管理Docker容器化的应用程序。可以理解为Docker在云中对应的服务就是ECS。...
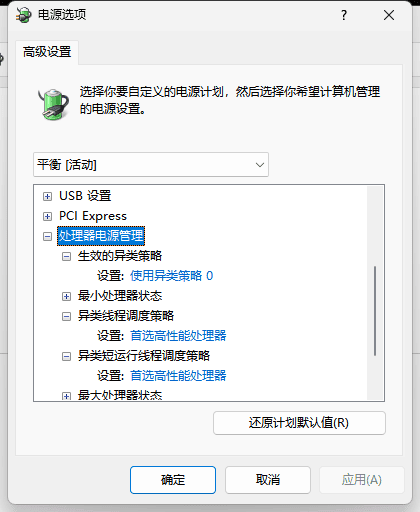
win10/win11 优先调用大核的电源计划性能设置
前言 大小核,即Intel 12代开始的P-core(性能核,一般叫大核)和E-core(能效核,一般叫小核)异核架构。说下个人理解,就是英特尔为了增加cpu性能,但是又因为架构和功耗的限制…...

模型实战(20)之 yolov8分类模型训练自己的数据集
yolov8分类模型训练自己的数据集 yolov8,一个实时快速的端到端的集检测、分割、分类、姿态识别于一体的视觉算法库/框架本文将给出yolov8 分类模型的数据集制作格式及训练流程 1. 环境搭建 关于虚拟环境的搭建真的是老生常谈了,给出一个简单的搭建流程吧#新建虚拟环境 conda …...

好消息!PMP纸质证书可以领取啦!(22年11月至23年8月)
上周五,中国国际人才交流基金会官方发布了《关于2022年11月和2023年3月、5月、8月PMI认证考试证书领取》的通知,具体内容如下: 之前顺利通过PMP/ACP/PgMP考试的同学抓紧时间,在5月24日—6月10日内进入官网上登记领取证书。 PMP考…...
)
select函数(Unix系统)
select函数(Unix系统) 一、函数格式二、参数及返回值2.1 struct fd_set 结构体2.1 struct timeval 结构体2.3 函数参数2.4 返回值 三、用法举例3.1 监控终端输入内容 一、函数格式 #include <sys/time.h>#include <sys/types.h>#include <…...
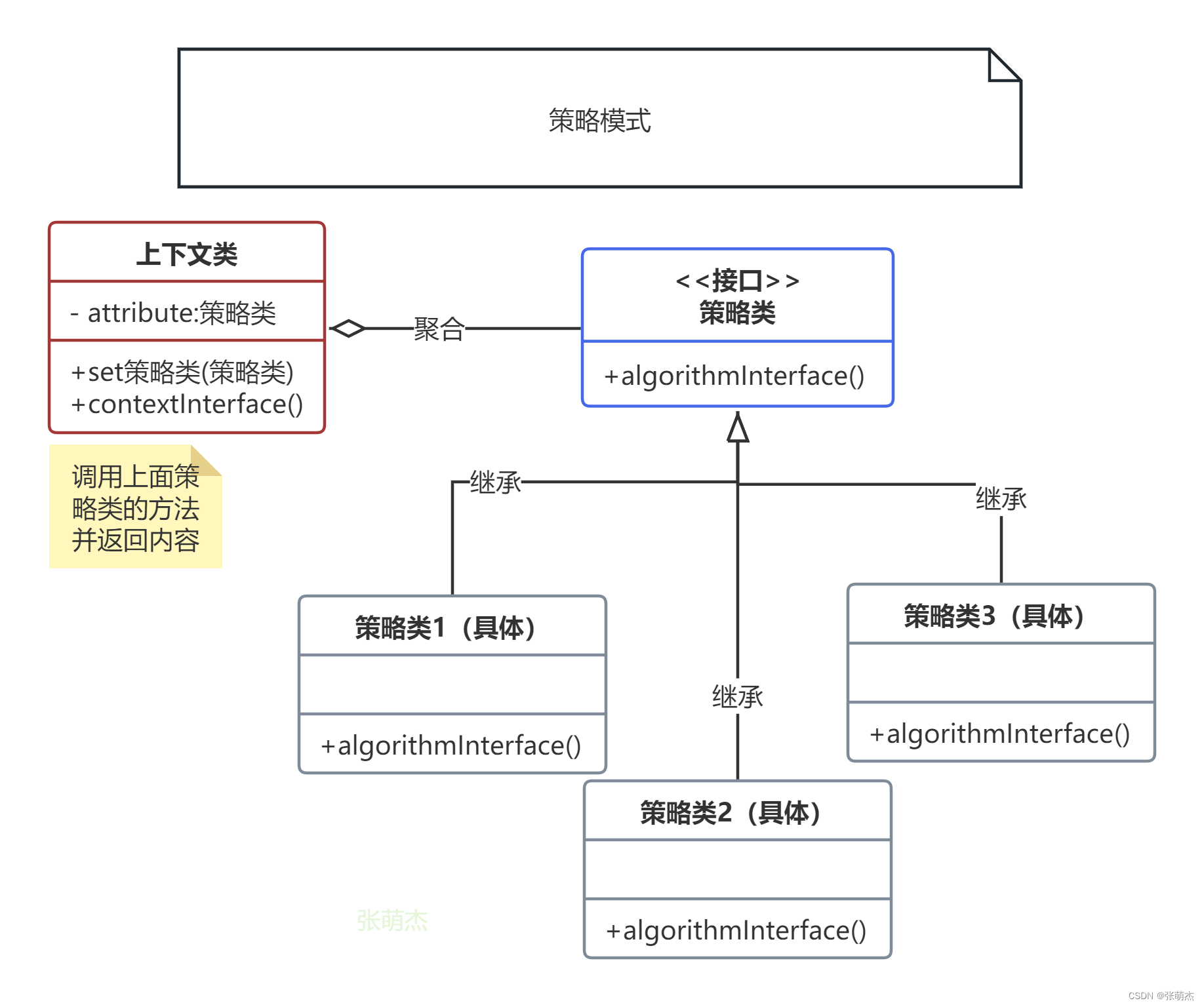
设计模式16——策略模式
写文章的初心主要是用来帮助自己快速的回忆这个模式该怎么用,主要是下面的UML图可以起到大作用,在你学习过一遍以后可能会遗忘,忘记了不要紧,只要看一眼UML图就能想起来了。同时也请大家多多指教。 策略模式(Strategy…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
