机器学习过拟合和欠拟合!看这一篇文章就够了 建议收藏!(上篇)
在机器学习中,有一项非常重要的概念,那就是:过拟合(Overfitting)和欠拟合(Underfitting)。
它们涉及到机器学习中常见的两种模型性能问题,分别表示模型在训练数据上表现得过于复杂或过于简单。
下面咱们先来简单聊聊关于过拟合和欠拟合的特征和防止性能问题的方法。
大家伙如果觉得还不错!可以点赞、转发安排起来,让更多的朋友看到。
ok,咱们一起来看看~
过拟合(Overfitting)
1、基本概念:过拟合指的是模型在训练数据上表现很好,但在未见过的测试数据上表现较差的情况。过拟合发生的原因是模型过于复杂,能够记住训练数据的细节和噪声,而不是学习数据的通用模式。
2、特征:
-
模型在训练数据上的准确度高。
-
模型在测试数据上的准确度较低。
-
模型的参数数量过多,容易记忆训练数据。
3、防止过拟合的方法:
-
数据集扩增:增加更多的训练数据,可以减少过拟合的风险。
-
正则化:通过添加正则化项,如L1正则化(Lasso)或L2正则化(Ridge),来惩罚模型参数的大小,使模型更简单。
-
特征选择:选择最重要的特征,降低模型的复杂度。
-
交叉验证:使用交叉验证来估计模型的性能,选择最佳的模型参数。
-
早停止:在训练过程中监控验证集的性能,当性能开始下降时停止训练,以防止过拟合。
欠拟合(Underfitting)
1、基本概念:欠拟合表示模型太过简单,无法捕获数据中的关键特征和模式。模型在训练数据和测试数据上的性能都较差。
2、特征:
-
模型在训练数据上的准确度较低。
-
模型在测试数据上的准确度也较低。
-
模型可能太简单,参数数量不足。
3、防止欠拟合的方法:
-
增加模型复杂度:使用更复杂的模型,例如增加神经网络的层数或增加决策树的深度。
-
增加特征:添加更多的特征或进行特征工程,以捕获更多数据的信息。
-
减小正则化强度:如果使用了正则化,可以降低正则化的强度,使模型更灵活。
-
调整超参数:调整模型的超参数,如学习率、批量大小等,以改善模型的性能。
-
使用更多数据:如果可能的话,增加训练数据可以提高模型的性能。
总的来说,过拟合和欠拟合都是需要非常注意的问题。
选择合适的模型复杂度、正则化方法和特征工程技巧可以帮助在训练机器学习模型时避免这些问题,获得更好的泛化性能。
过拟合-小小案例
过拟合是指模型在训练数据上表现得很好,但在未见过的数据上表现不佳,因为它过于复杂,过度拟合了训练数据中的噪声。
下面用一个简单的多项式回归示例来演示过拟合,并提供解决方法。
首先,让我们生成一个模拟的数据集,然后尝试使用高阶多项式回归模型拟合它:
import numpy as np
import matplotlib.pyplot as plt# 生成模拟数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.randn(80) * 0.1# 使用高阶多项式回归模型拟合数据
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_errordegrees = [1, 15] # 两个不同的多项式次数plt.figure(figsize=(12, 6))
for i, degree in enumerate(degrees):ax = plt.subplot(1, 2, i + 1)model = make_pipeline(PolynomialFeatures(degree), LinearRegression())model.fit(X, y)# 绘制拟合曲线X_test = np.linspace(0, 5, 100)[:, np.newaxis]y_pred = model.predict(X_test)plt.scatter(X, y, color='blue')plt.plot(X_test, y_pred, color='red', linewidth=2)plt.title(f'Degree {degree} Polynomial Regression')# 计算均方误差mse = mean_squared_error(y, model.predict(X))plt.text(4, 0.4, f"MSE: {mse:.2f}", fontsize=12)plt.show()上面示例中,首先使用了一个简单的线性模型(多项式次数为1),然后使用了一个高阶多项式模型(多项式次数为15)。可以看到,高阶多项式模型在训练数据上表现得非常好,但在数据边界之外的区域出现了极端的波动,这是典型的过拟合现象。
为了解决过拟合问题,可以采取以下几种方法:
-
减小模型复杂度:降低多项式的次数或使用更简单的模型,以减少模型的复杂性。
-
增加训练数据:收集更多的训练数据,以提供模型更多的信息,减少过拟合的风险。
-
正则化:使用正则化技术,如L1正则化(Lasso)或L2正则化(Ridge),来限制模型参数的大小,防止过拟合。
-
交叉验证:使用交叉验证来评估模型的性能,以便及早检测并解决过拟合问题。
过拟合问题通常需要综合考虑模型复杂度、数据量和正则化等因素来解决。选择合适的模型和超参数是解决过拟合的关键。
欠拟合-小小案例
欠拟合是指模型在训练数据上表现不佳,不能够捕获数据的复杂性和模式。这通常是由于模型过于简单或者特征不足的原因导致的。
首先,生成一个模拟的数据集,然后尝试使用线性回归模型拟合它,但使用一个过于简单的模型:
import numpy as np
import matplotlib.pyplot as plt# 生成模拟数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.randn(80) * 0.1# 使用线性回归模型拟合数据
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errormodel = LinearRegression()
model.fit(X, y)# 绘制拟合曲线
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red', linewidth=2)
plt.title('Linear Regression - Underfitting')
plt.show()# 计算均方误差
mse = mean_squared_error(y, model.predict(X))
print(f"Mean Squared Error: {mse}")在上面的示例中,我们使用了一个线性回归模型来拟合一个非线性的数据集(sin函数)。由于线性模型太简单,不能捕获数据的复杂性,导致了欠拟合。
为了解决欠拟合问题,可以采取以下几种方法:
1、增加模型复杂度:可以尝试使用更复杂的模型,例如多项式回归,以更好地拟合数据的形状。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline# 使用多项式回归
degree = 5
polyreg = make_pipeline(PolynomialFeatures(degree), LinearRegression())
polyreg.fit(X, y)# 绘制多项式回归拟合曲线
plt.scatter(X, y, color='blue')
plt.plot(X, polyreg.predict(X), color='red', linewidth=2)
plt.title(f'Polynomial Regression (Degree {degree})')
plt.show()# 计算均方误差
mse_poly = mean_squared_error(y, polyreg.predict(X))
print(f"Mean Squared Error (Polynomial Regression): {mse_poly}")2、增加特征:如果特征不足以描述数据的复杂性,可以尝试添加更多特征,以便模型能够更好地拟合数据。
3、减小正则化:如果您在使用正则化(如L1或L2正则化)来防止过拟合,可以考虑减小正则化强度,以允许模型更好地拟合数据。
欠拟合问题的解决方法通常涉及增加模型复杂度或改进特征工程,以使模型更能够捕获数据的潜在模式。
不过,需要注意,增加模型复杂度也可能导致过拟合,因此需要谨慎选择模型和调整超参数。
最后
今天介绍了过拟合和欠拟合,以及代码案例,并且给出的解决方案。
喜欢的朋友可以收藏、点赞、转发起来!
相关文章:
)
机器学习过拟合和欠拟合!看这一篇文章就够了 建议收藏!(上篇)
在机器学习中,有一项非常重要的概念,那就是:过拟合(Overfitting)和欠拟合(Underfitting)。 它们涉及到机器学习中常见的两种模型性能问题,分别表示模型在训练数据上表现得过于复杂或…...
关于阳光雨露外派联想的面试感想
最近在找工作,接到了一个阳光雨露外派联想的面试邀请。说实在的一开始就有不对劲的感觉。想必这就是大厂的自信吧,上就问能不能现场面试,然后直接发面试邀请。这时候我倒是没觉得有啥问题。 然后今天就去面试去了,住的比较偏&…...

深度神经网络介绍与实战
一、介绍 深度神经网络(Deep Neural Networks,DNNs)是一种强大的机器学习算法,被广泛应用于计算机视觉、自然语言处理、语音识别等领域。它是人工神经网络的一种扩展,包含多个隐藏层,每一层都由多个神经元组成。 与传统的机器学习算法相比,深度神经网络具有以下特点:…...
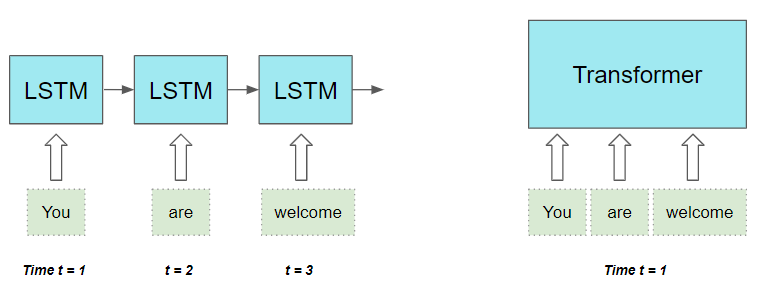
图解 Transformer
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学. 针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 汇总合集&…...

SpringCloud配置文件bootstrap不生效问题解决
解决方案: 情况一、SpringBoot 版本 小于 2.4.0 版本,添加以下依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-context</artifactId> </dependency> 情况二、SpringBoot…...

Java面试八股之自旋是什么意思
Java中的自旋是什么意思 自旋是多线程编程中的一种同步机制,尤其在Java中与锁的实现密切相关。当一个线程尝试获取某个锁(如内置锁或显式锁)时,如果锁已被其他线程持有,通常的做法是将该线程置于阻塞状态,…...

做好随时离开的准备:前一天还在为618加班到凌晨,第二天就被裁了
今日感悟 最近,一则令人唏嘘的新闻在网络上引起了广泛关注:一名员工前一天还在为618大促活动加班到凌晨,身心疲惫,然而第二天却收到了裁员通知,顿时陷入了失业的困境。 这则新闻不仅揭示了职场竞争的残酷现实ÿ…...

利用ESP32(Arduino IDE)向匿名上位机发送欧拉角
文章目录 一. 匿名上位机介绍二. 匿名协议说明1. 匿名协议官方说明文档2. 协议说明 三. 向匿名上位机发送数据(基于Arduino IDE的esp32)四. 运行效果 一. 匿名上位机介绍 匿名上位机官方介绍视频 匿名上位机官方下载 二. 匿名协议说明 1. 匿名协议官方说明文档 官方对于协…...
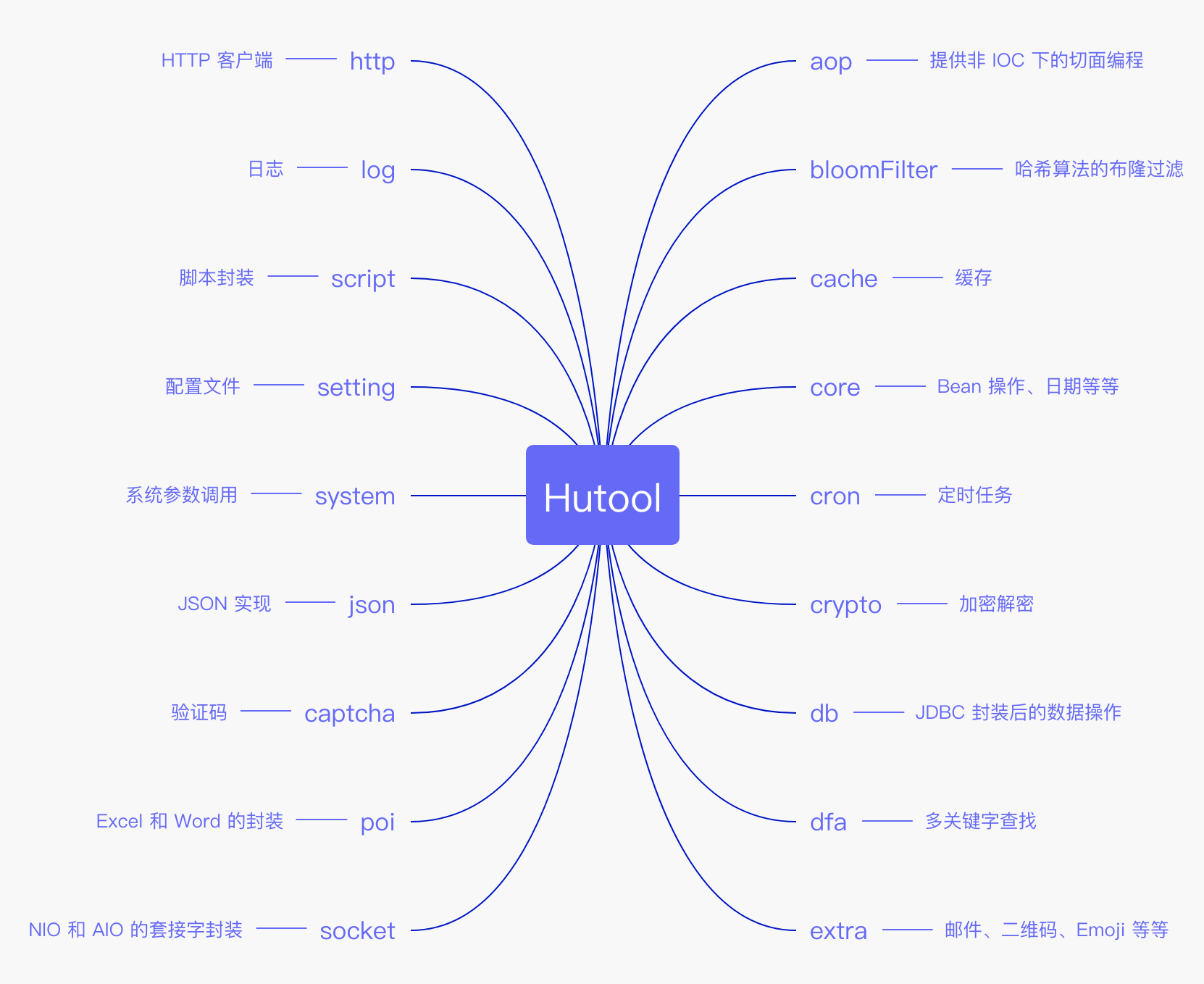
Java开发工具类(JDK、Hutool、Guava)
目录 Java开发常用的工具类1、JDK自带程序读取控制台输入内容(调试程序或者学习的时候比较有用)Arrays工具类 数组转集合Collections 集合工具类 排序Collections 集合工具类 查找Lambda表达式 操作集合 收集、转map、分组 2、Apache 的 commons-lang3 和…...

TCP协议的相关特性
目录 正文: 1.可靠性 2.连接管理 3.滑动窗口 4.流量控制 5.拥塞控制 6.延迟应答 7.捎带应答 总结: 正文: 1.可靠性 TCP协议是一个有连接,可靠传输,面向字节流,全双工的协议。其中可靠传输的实现…...

Lombok,一款超级强大的Java工具库
在软件开发过程中,繁琐的模板代码经常让开发者感到烦恼。 Lombok 是一款 Java 库,能够帮助开发者减少这些冗余代码,提高开发效率。本文将介绍 Lombok 的基本概念、安装和配置方法,以及如何在实际项目中使用它。 Lombok 是什么 L…...

FreeBSD下使用原生虚拟机管理器bhyve
hbyve简介 自 FreeBSD 10.0-RELEASE 起,BSD 许可的 bhyve 虚拟机管理器已成为底层系统不可或缺的一部分。bhyve 强大而灵活,支持多种客户机操作系统,涵盖 FreeBSD、OpenBSD 以及多个 Linux 发行版。在默认配置下,bhyve 提供对串行…...

CTFshow之文件上传web入门151关-161关解密。包教包会!!!!
这段时间一直在搞文件上传相关的知识,正好把ctf的题目写了写,也算是给自字做个总结! 不过ctf有一个缺点就是所有的测试全部是黑盒测试,无法从代码层面和大家解释,我找个时间把upload-labs靶场做一做给大家讲讲白盒的代…...

【学习记录】服务器转发使用tensorboard
场景 代码在服务器上运行,想使用tensorboard查看训练的过程。 但是服务器上不能直接访问地址,所以要转发端口到本地,从而在本地网页中能够打开tensorboard。 参考:https://zhuanlan.zhihu.com/p/680596384 这时我们需要建立本地…...

类型转换之显式转换
显式转换——>手动处理,强制转换 括号强转 作用:一般情况下,将高精度的类型转换为低精度。 语法:变量类型 变量名 (变量类型)变量; 注意:精度问题,范围问题。 括号强转&#x…...

Mybatis多表查询,报错:Column ‘id‘ in field list is ambiguous
错误原因: Mybatis 多表查询时,多个表有相同名字的字段,比如 id,名字重复,没有指定对应的表名。 有两个地方需要注意:(1)将其中一个重复字段的 Mybatis的 column 修改为其他的名字。(2)字段加上对应的表名…...
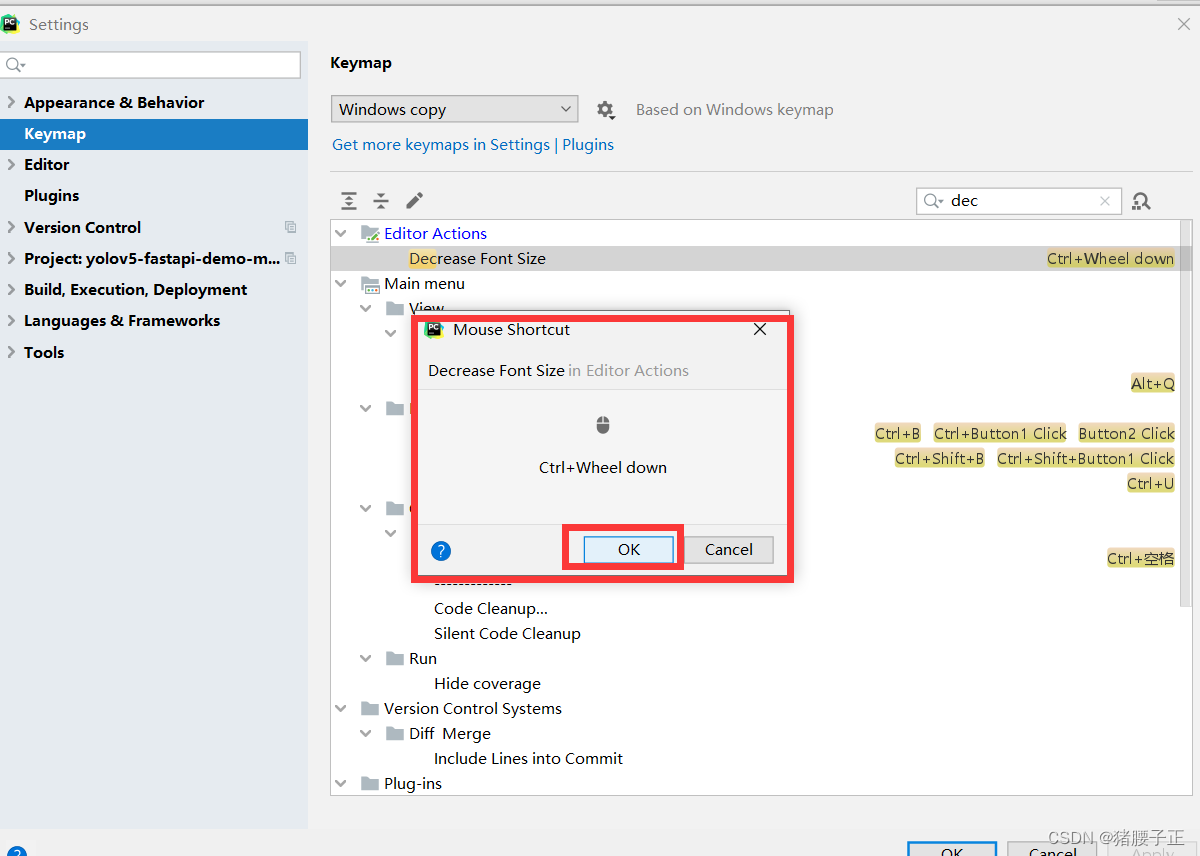
PyCharm面板ctrl+鼠标滚轮放大缩小代码
1.【File】➡【Settings】 2.点击【Keymap】,在右边搜索框中搜incre,双击出现的【Increase Font Size】 3.在弹出的提示框中选择【Add Mouse Shortcut】 4.弹出下面的提示框后,键盘按住【ctrl】,并且上滑鼠标滚轮。然后点击【O…...

【Qt】数据库(一)SQLITE创建、增删查改
填坑1:如何连续插入 汇总SQlite语句 创建表格:create table <table_name> (f1 type1, f2 type2,…); 增:insert into <table_name> values (value1, value2,…); 改:update <table_name> set <f1value1>,…...
)
【模拟面试问答】力扣165题:比较版本号(逐个比较与双指针法详解及模拟面试问答)
在本篇文章中,我们将详细解读力扣第165题“比较版本号”。通过学习本篇文章,读者将掌握如何使用多种方法来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释和ASCII图解,以便于理解。 问题描述 …...
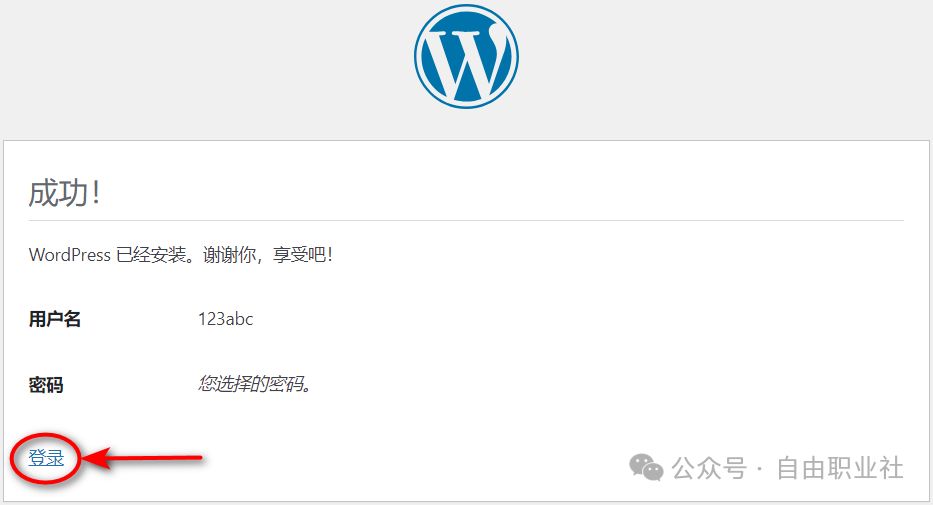
用PhpStudy在本地电脑搭建WordPress网站教程(2024版)
对新手来说,明白了建站3要素后,如果直接购买域名、空间去建站,因为不熟练,反复测试主题、框架、插件等费时费力,等网站建成可能要两三个月,白白损失这段时间的建站费用。那么新手怎么建测试网站来练手呢&am…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
