备战秋招c++ 【持续更新】
T1 牛牛的快递

原题链接:牛牛的快递_牛客题霸_牛客网 (nowcoder.com)
题目类型:模拟
审题&确定思路:
1、超过1kg和不足1kg有两种不同收费方案 ---- 起步价问题
2、超出部分不足1kg的按1kg计算 ----- 向上取整
3、向上取整的实现思路
a:使用库函数ceil() //要包含头文件 #inlcude<cmath>
b:强转 + 判断
if(ch - (int)ch > 0) // eg: (int)1.5 = 1
//说明需要向上取整参考代码
#include <iostream>
#include <cmath>
using namespace std;int main() {float a;char b;cin >>a>>b;if(a >1){int ret = ceil(a)-1;cout<<(b == 'y' ? 25+ret : ret+20)<<endl;}else {cout <<(b == 'y' ? 25: 20)<<endl;}return 0;
}T2最小花费爬楼梯
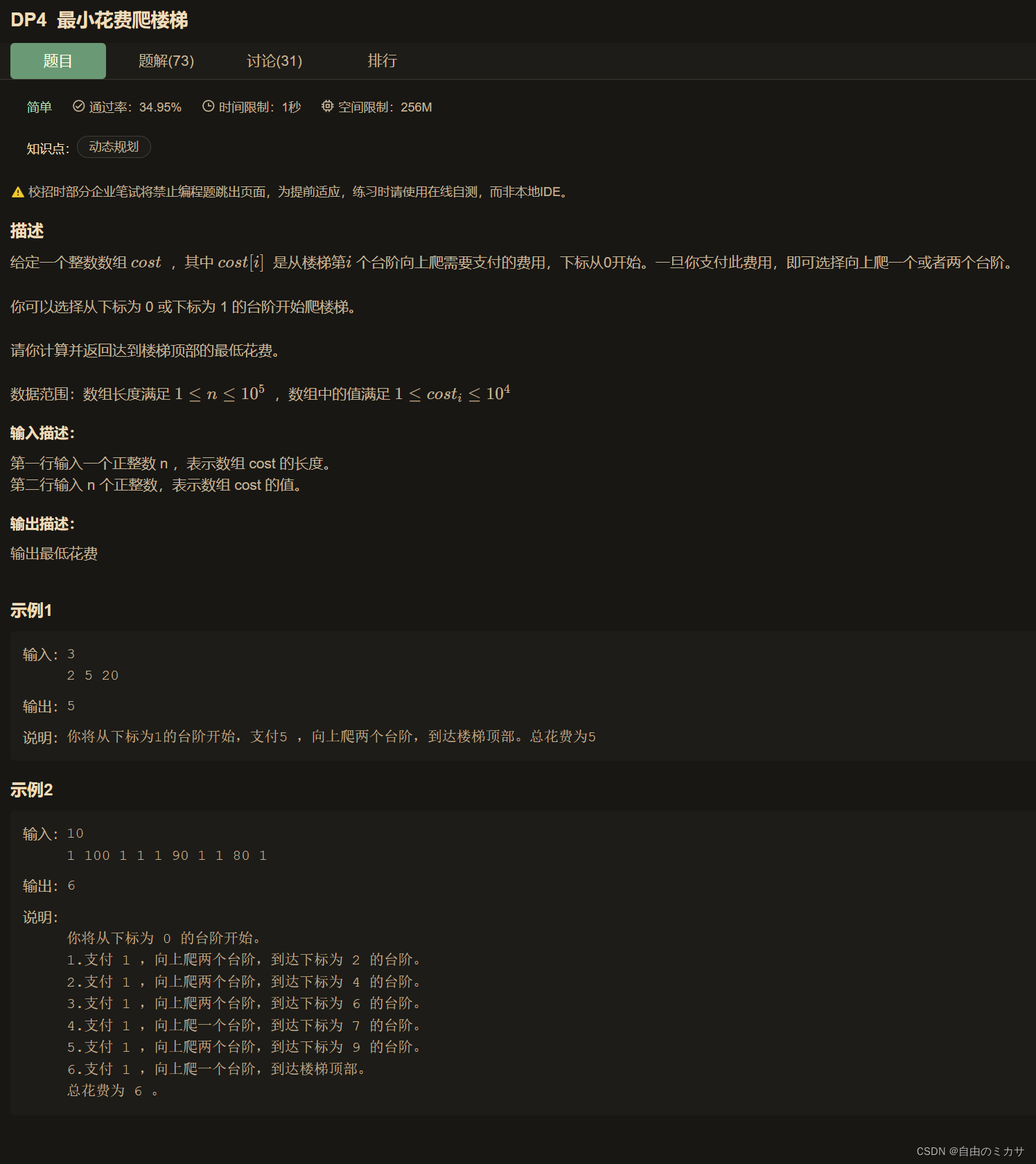
原题链接:最小花费爬楼梯_牛客题霸_牛客网 (nowcoder.com)
题目类型:dp
审题&确定思路:
1、确定状态表示:dp[i]表示 以i位置为结尾,从0或1下标开始到这个位置的最小花费
2、确定状态转移方程:以i位置为结尾进行思考。因为可以选择跳一层或者两层,说明当站在i这层位置的时候,可能是从前一层或者前两层跳上来的。要使得当前i位置的花费最小,则要对比从前一层跳过来的最低花费和从前两层跳过来的最低花费 谁更小 再加上往上跳对应要支付的花费,就得到当前层最低花费
其中最低花费对应状态表示dp[i]
将上述关系转化为代码
dp[i] = min(dp[i-1] +cost[i-1] ,dp[i-2]+cost[i-2]);3、确定填表顺序
因为需要用到前两层的dp信息,所以从左往右填表
4、处理边界情况
因为下标从0开始,可以从0也可以从1开始跳,而刚站上这层楼梯时是不需要花费的,往上跳才需要支付这层的花费。所以dp[0]和dp[1]都为0
接着填表从i = 2开始,就不会发生越界问题。
参考代码:
#include <iostream>
#include<vector>
#include<cmath>
using namespace std;int main() {int n;cin>>n;vector<int>cost(n);for(int i = 0;i<n;i++){cin>>cost[i];}vector<int>dp(n+1);dp[0] = 0;dp[1] = 0;for(int i =2;i<=n;i++){dp[i] = min(dp[i-1] +cost[i-1] ,dp[i-2]+cost[i-2]);}cout<<dp[n];return 0;}
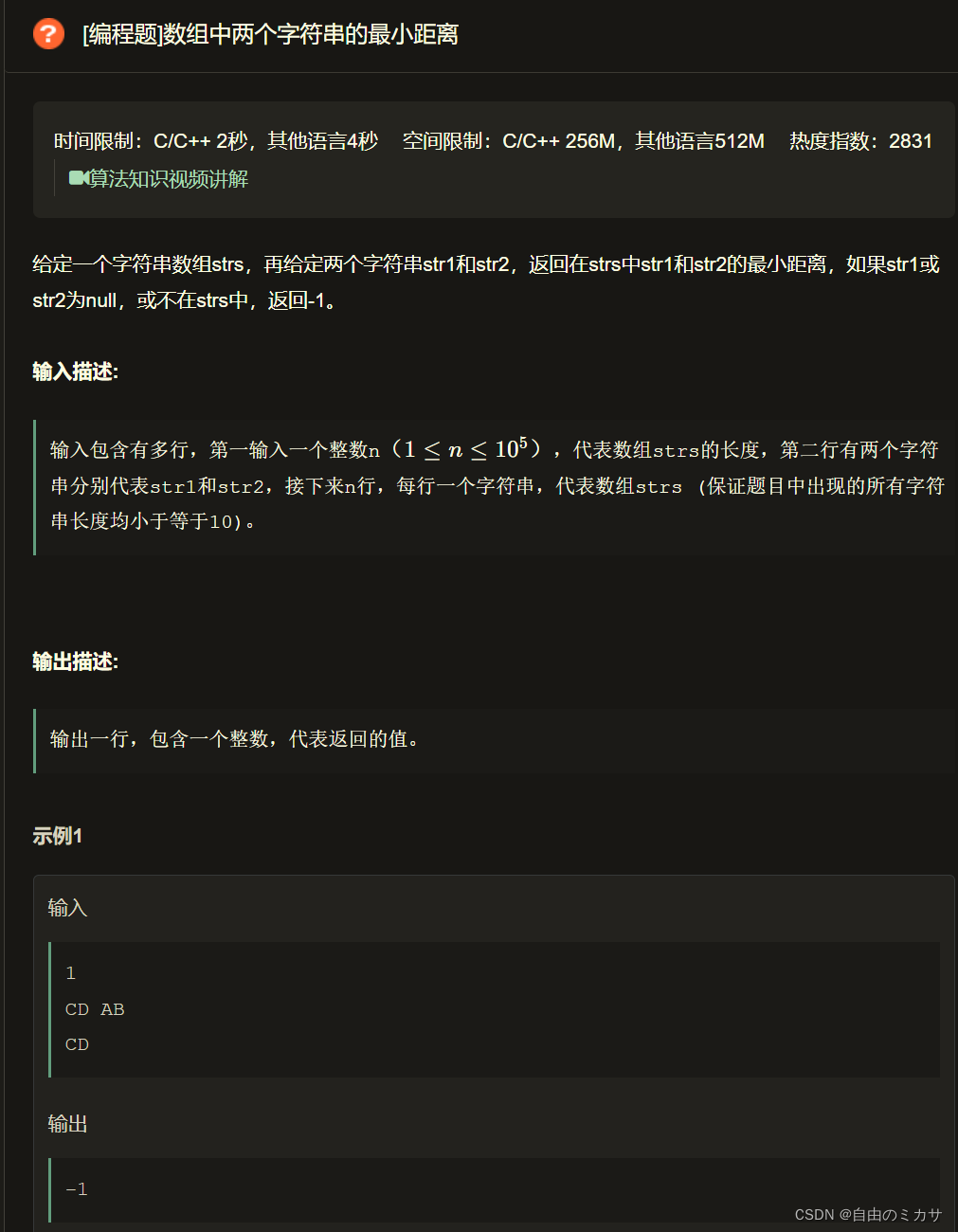
T3数组中两个字符串的最小距离

原题链接:数组中两个字符串的最小距离__牛客网 (nowcoder.com)
题目类型:贪心、字符串
审题&确定思路:
1、题目说的strs其实是个字符串类型的数组,里面存放的都是字符串
2、暴力解法,先固定一个字符串str1,然后再搜索str2,计算两个字符串间的距离,并与记录的最短距离进行比较
3、优化思路:贪心 ---- 使用一个或多个变量来表示前驱的信息,即预处理信息。(最终达到优化一层循环的效果)
4、优化实现方法:设置两个int变量prev1 和 prev2 分别记录str1和str2最后一次出现的下标。
5、优化效果:可以不用创建字符串数组来记录strs中的字符串,而是直接用一个字符串来模拟当前遍历到的strs字符串数组中的字符串。因为prev1 和 prev2 这两个变量已经记录了信息,strs遍历完的元素不会再次遍历,所以可以省去构建数组的这一步。
参考代码:
#include <iostream>
#include<vector>
#include<cmath>
using namespace std;int main() {//处理输入信息string str1 ,str2;int n;cin >>n>>str1>>str2;//使用一个字符串变量来表示当前遍历到的字符串string s;//设置变量记录前驱信息,优化一层循环//初始化为-1是为了区别str1/str2是否在strs中出现int prev1 = -1,prev2 = -1;//ret 记录两字符串间的最短距离,为不影响最短距离的比较,所以设置个较大值//0x3f3f3f3f是常用数据,可近似看做无限大值int ret = 0x3f3f3f;for(int i = 0;i<n;i++){cin >>s;if(s == str1){prev1 = i;if(prev2 != -1)ret = fmin(ret,abs(prev2 - prev1));}else if(s == str2) //要写出 s == str2 不能直接写else if,因为除了str1和str2,strs中的字符串(即s)还有其他样式的{prev2 = i;if(prev1 != -1)ret = fmin(ret,abs(prev2 - prev1));}}//判断是否str1和str2都在strs中出现了if(ret != 0x3f3f3f){cout << ret<<endl;}else {cout<<-1<<endl;}return 0;}相关文章:

备战秋招c++ 【持续更新】
T1 牛牛的快递 原题链接:牛牛的快递_牛客题霸_牛客网 (nowcoder.com) 题目类型:模拟 审题&确定思路: 1、超过1kg和不足1kg有两种不同收费方案 ---- 起步价问题 2、超出部分不足1kg的按1kg计算 ----- 向上取整 3、向上取整的实现思路…...

整数拆分~
way:process //上一个拆出来的数是pre //还剩下rest需要去拆 //返回拆解的方法数 #include<iostream> using namespace std;//上一个拆出来的数是pre //还剩下rest需要去拆 //返回拆解的方法数 int process(int pre, int rest) {if(rest0) return 1;//因为后…...
【Qt Creator】跨平台的C++图形用户界面应用程序开发框架---QT
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1.互联网的核心岗位以及职…...
KingbaseES数据库物理备份还原sys_rman
数据库版本:KingbaseES V008R006C008B0014 简介 sys_rman 是 KingbaseES 数据库中重要的物理备份还原工具,支持不同类型的全量备份、差异备份、增量备份,保证数据库在遇到故障时及时使用 sys_rman 来恢复到数据库先前状态。 文章目录如下 1.…...

【CV】视频图像背景分割MOG2,KNN,GMG
当涉及背景分割器(Background Subtractor)时,Mixture of Gaussians(MOG2)、K-Nearest Neighbors(KNN)和Geometric Multigid(GMG)是常用的算法。它们都用于从视频流中提取…...

使用 Python 简单几步去除 PDF 水印
推荐一个AI网站,免费使用豆包AI模型,快去白嫖👉海鲸AI 在处理 PDF 文件时,水印有时会影响文件的可读性或美观性。幸运的是,Python 提供了多种库来操作 PDF 文件,其中 PyMuPDF(又名 fitz…...

【香橙派 AIpro】OrangePi AIpro :教育、机器人、无人机领域的超级AI大脑,华为昇腾处理器驱动的AI开发板新标杆
【OrangePi AIpro:教育、机器人、无人机领域的超级AI大脑,华为昇腾处理器驱动的AI开发板新标杆】 文章目录 一、开箱与初印象1. 初印象2. 上手开机3. 安装和运行 TightVNC 远程桌面3.1. 安装 TightVNC 服务器3.2. 启动 VNC 服务器3.3. 在 Windows 上使用…...

【Mac】 CleanMyMac X for mac V4.15.2中文修复版安装教程
软件介绍 CleanMyMac X是一款为Mac设计的优秀软件,旨在帮助用户优化其设备的性能并提供清理和维护功能。以下是 CleanMyMac X的一些主要功能和特点: 1.系统性能优化:软件可以扫描和修复潜在的性能问题,包括无效的登录项、大文件…...

单片机通信协议(1):SPI简介
关于SPI SPI(串行外设接口)是板载设备间通信接口之一。它是由摩托罗拉公司(飞思卡尔半导体)推出的。由于其简单性和通用性,它被纳入各种外围设备中,并与飞利浦I2C总线并列。 SPI的三线或四线信号数量比IIC…...
免税商品优选购物商城,基于 SpringBoot+Vue+MySQL 开发的前后端分离的免税商品优选购物商城设计实现
目录 一. 前言 二. 功能模块 2.1. 登录界面 2.2. 管理员功能模块 2.3. 商家功能模块 2.4. 用户前台功能模块 2.5. 用户后台功能模块 三. 部分代码实现 四. 源码下载 一. 前言 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过…...
概述)
京准电子、NTP电子时钟系统(网络时钟系统)概述
京准电子、NTP电子时钟系统(网络时钟系统)概述 京准电子、NTP电子时钟系统(网络时钟系统)概述 时钟系统工作原理是由母钟接收GPS/北斗卫星的时间信息,母钟通过串口和NTP以太网接口为其他各系统提供统一的标准时间信号&…...
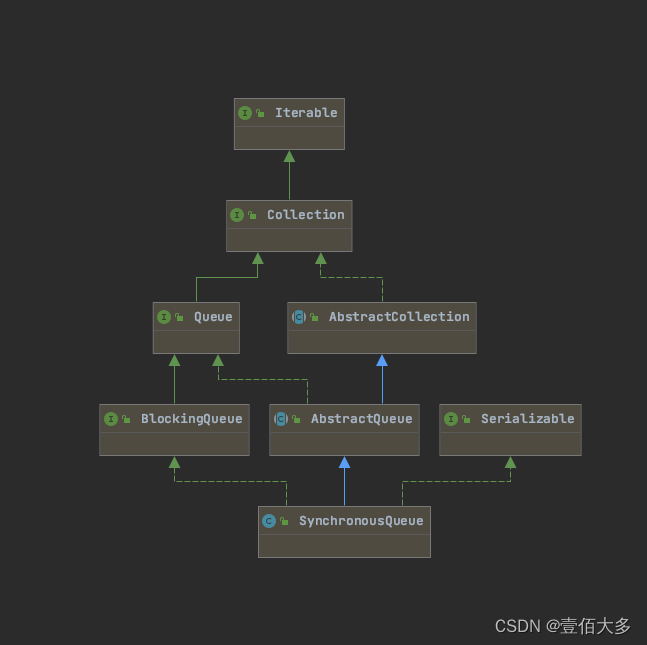
【常用的队列总结】
文章目录 队列的介绍Queue队列的基本概念与操作队列的基本概念 常见的队列介绍非阻塞队列LinkedList:ArrayDeque:PriorityQueue: 阻塞队列ArrayBlockingQueueLinkedBlockingQueuePriorityBlockingQueue DelayQueueSynchronousQueue 队列的介绍 Queue队列的基本概念与操作 在 …...
)
机器学习过拟合和欠拟合!看这一篇文章就够了 建议收藏!(上篇)
在机器学习中,有一项非常重要的概念,那就是:过拟合(Overfitting)和欠拟合(Underfitting)。 它们涉及到机器学习中常见的两种模型性能问题,分别表示模型在训练数据上表现得过于复杂或…...
关于阳光雨露外派联想的面试感想
最近在找工作,接到了一个阳光雨露外派联想的面试邀请。说实在的一开始就有不对劲的感觉。想必这就是大厂的自信吧,上就问能不能现场面试,然后直接发面试邀请。这时候我倒是没觉得有啥问题。 然后今天就去面试去了,住的比较偏&…...

深度神经网络介绍与实战
一、介绍 深度神经网络(Deep Neural Networks,DNNs)是一种强大的机器学习算法,被广泛应用于计算机视觉、自然语言处理、语音识别等领域。它是人工神经网络的一种扩展,包含多个隐藏层,每一层都由多个神经元组成。 与传统的机器学习算法相比,深度神经网络具有以下特点:…...
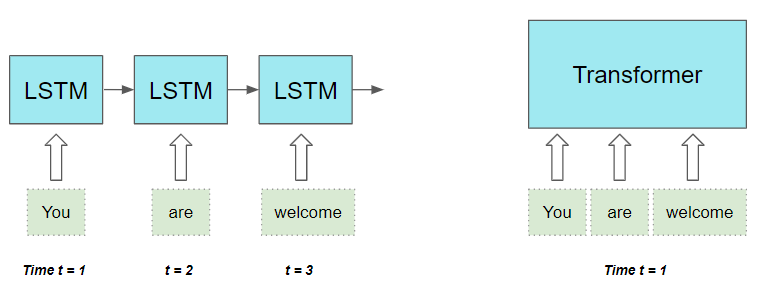
图解 Transformer
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学. 针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 汇总合集&…...

SpringCloud配置文件bootstrap不生效问题解决
解决方案: 情况一、SpringBoot 版本 小于 2.4.0 版本,添加以下依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-context</artifactId> </dependency> 情况二、SpringBoot…...

Java面试八股之自旋是什么意思
Java中的自旋是什么意思 自旋是多线程编程中的一种同步机制,尤其在Java中与锁的实现密切相关。当一个线程尝试获取某个锁(如内置锁或显式锁)时,如果锁已被其他线程持有,通常的做法是将该线程置于阻塞状态,…...

做好随时离开的准备:前一天还在为618加班到凌晨,第二天就被裁了
今日感悟 最近,一则令人唏嘘的新闻在网络上引起了广泛关注:一名员工前一天还在为618大促活动加班到凌晨,身心疲惫,然而第二天却收到了裁员通知,顿时陷入了失业的困境。 这则新闻不仅揭示了职场竞争的残酷现实ÿ…...

利用ESP32(Arduino IDE)向匿名上位机发送欧拉角
文章目录 一. 匿名上位机介绍二. 匿名协议说明1. 匿名协议官方说明文档2. 协议说明 三. 向匿名上位机发送数据(基于Arduino IDE的esp32)四. 运行效果 一. 匿名上位机介绍 匿名上位机官方介绍视频 匿名上位机官方下载 二. 匿名协议说明 1. 匿名协议官方说明文档 官方对于协…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
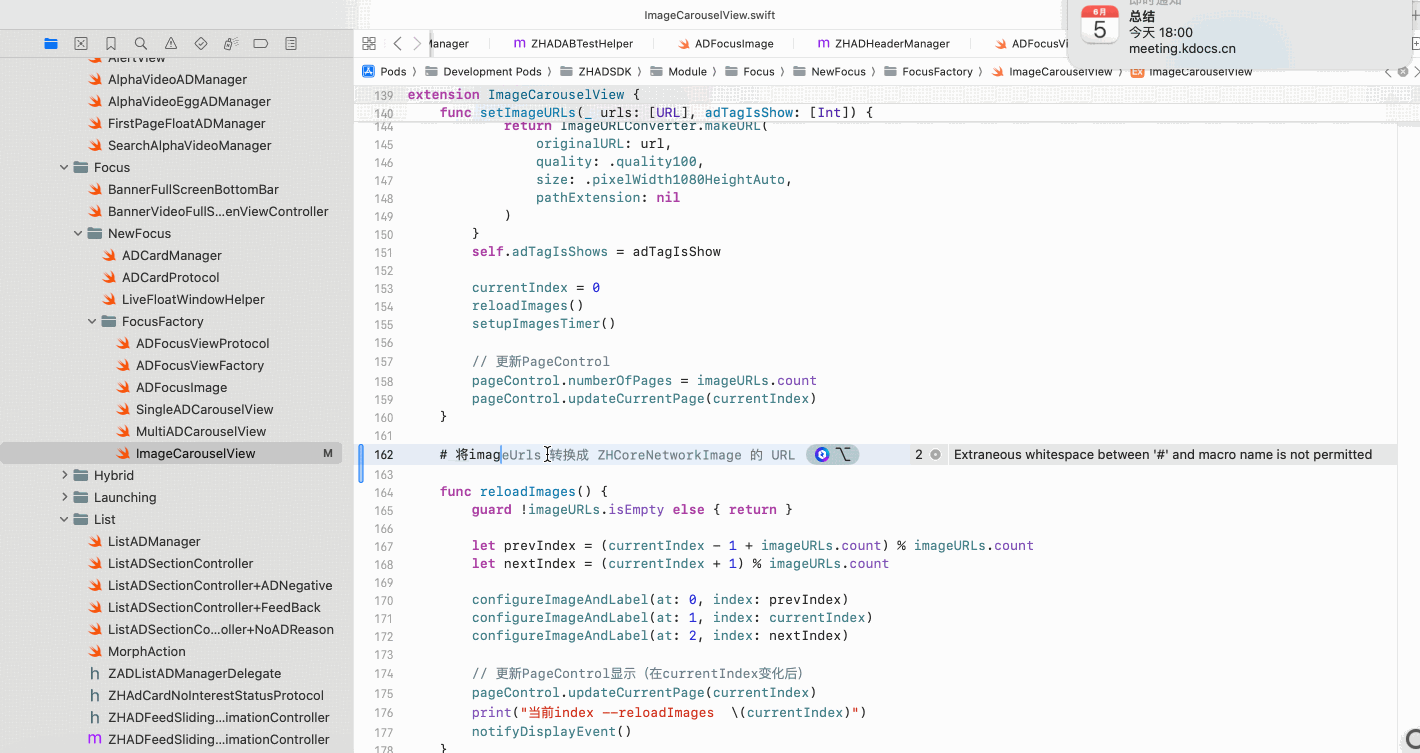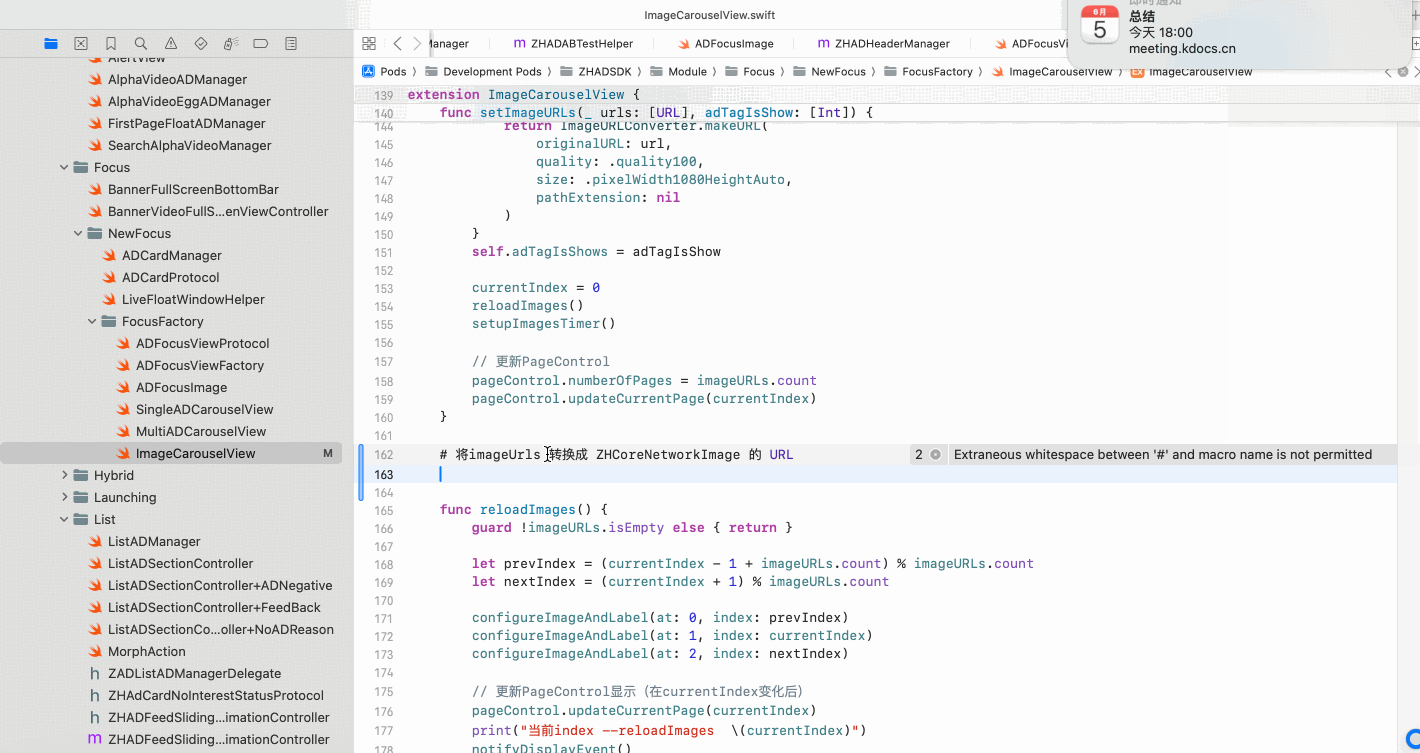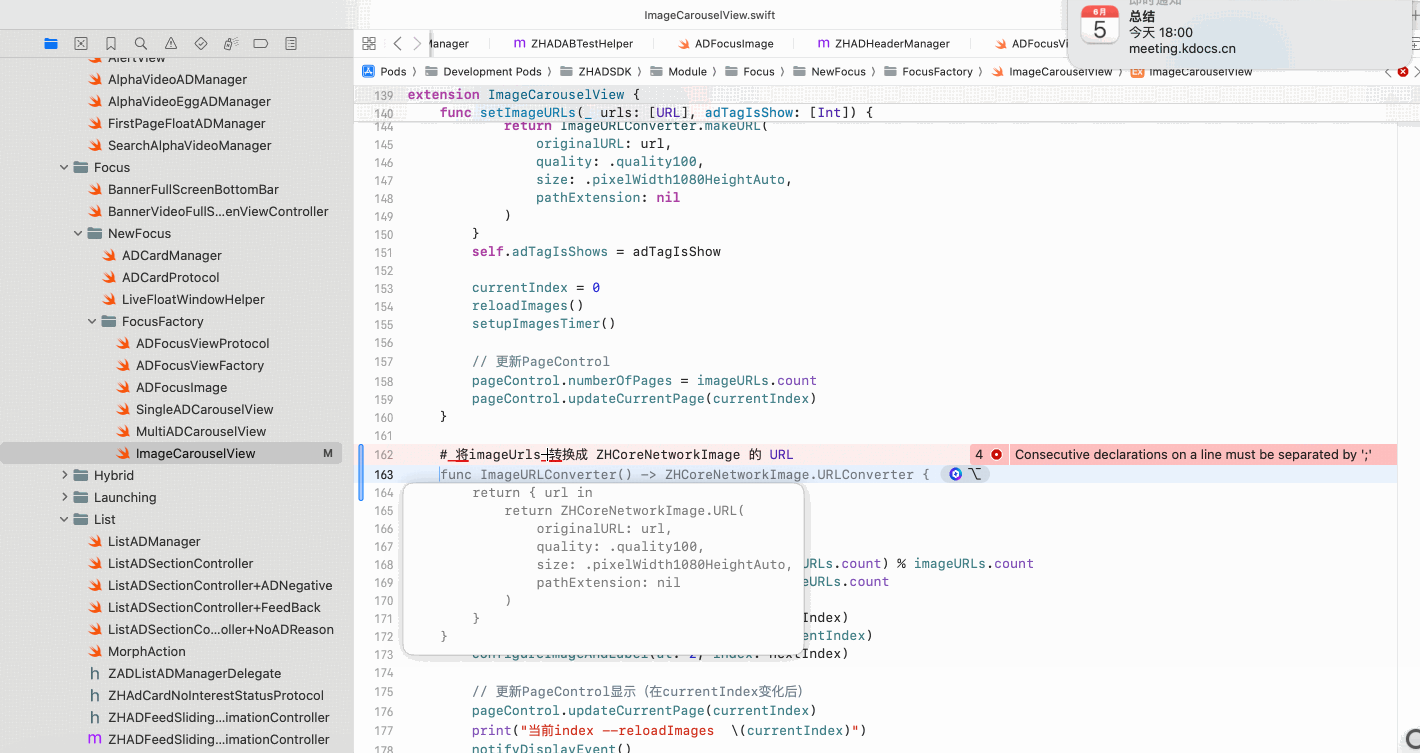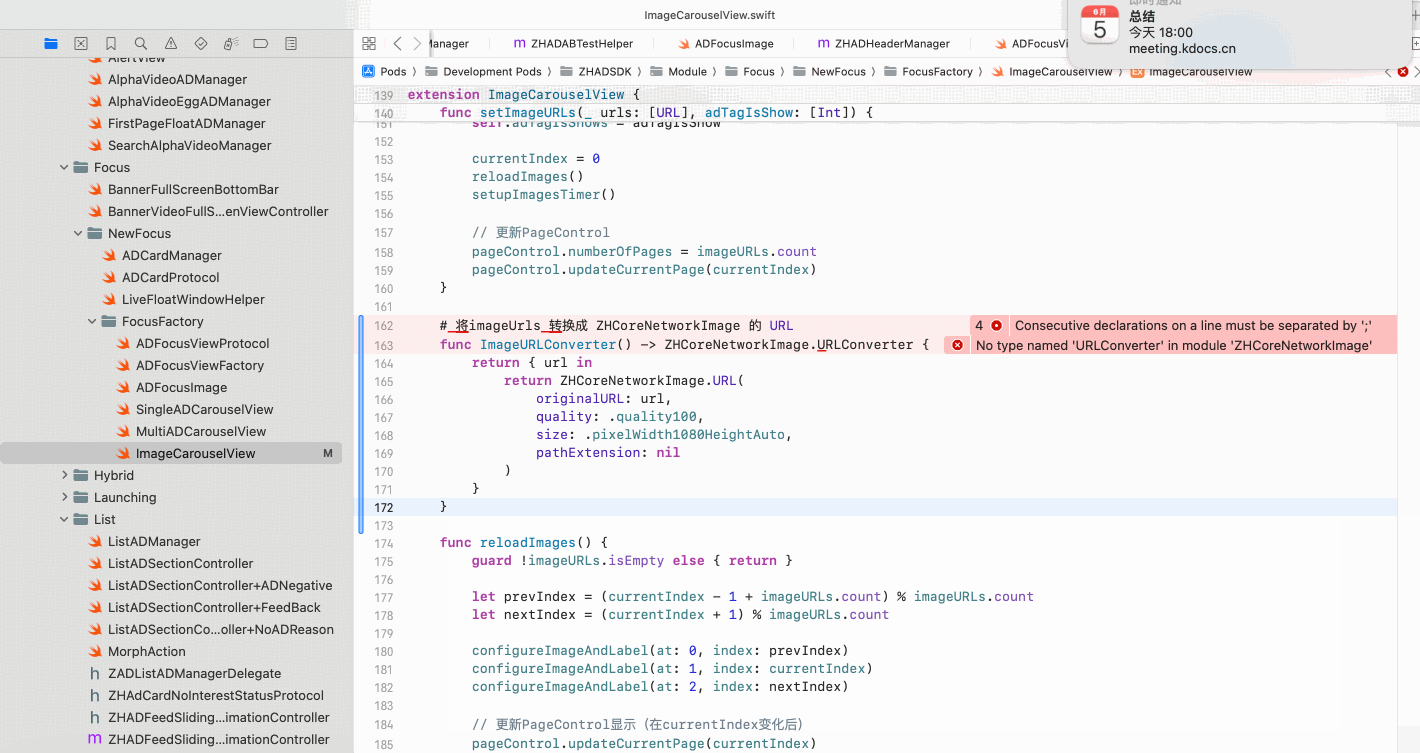
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...