分布式事务解决方案(最终一致性【可靠消息解决方案】)
可靠消息最终一致性解决方案
可靠消息最终一致性分布式事务解决方案指的是事务的发起方执行完本地事务之后,发出一条消息,事务的参与方,也就是消息的消费者一定能够接收到这条消息并且处理完成,这个方案强调的是只要事务发起方将消息发送给事务参与者,事务参与方就一定能够执行完成,事务最终达到一致性的状态
适用的场景
适用于消息数据能够独立存储,能够减低系统之间耦合度,并且业务对数据一致性的时间敏感度高的场景
需要实现的服务模式
需要实现的服务模式是可查询操作和幂等操作,需要参与分布式事务的业务服务提供可查询自身事务状态的接口,发生异常时,能够通过接口查询具体的事务状态,这就是可查询操作,参与分布式事务的各个业务接口需要保证数据操作的幂等性。
方案的执行流程
可靠消息最终一致性方案中,事务发起方执行完本地事务后,通过可靠消息服务将消息发送给事务参与方,事务参与方收到消息后,一定能够成功执行,这里的可靠消息服务可以通过本地消息表实现,也可以通过RocketMq消息队列实现
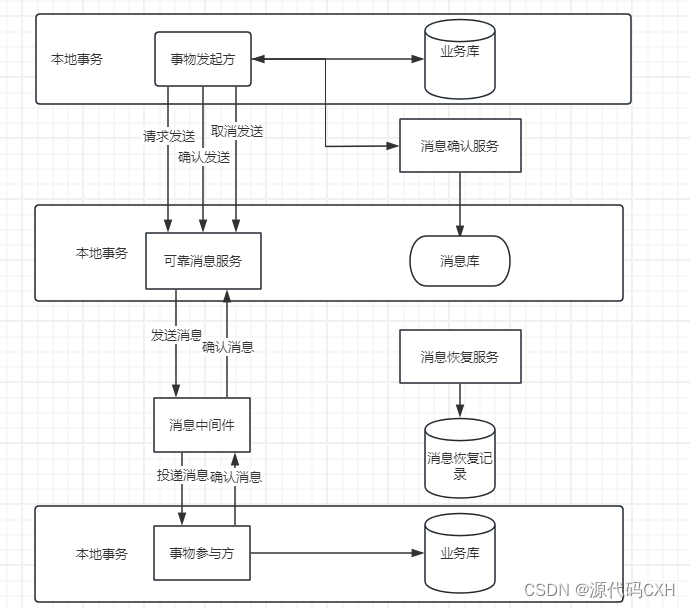
首先,事务发起方将消息发送给可靠消息服务,这里的可靠消息服务可以基于本地数据表实现,也可以基于消息队列中间件实现。然后,事务参与方从可靠消息服务中接收消息。事务发起方和可靠消息服务之间、可靠消息服务和事务参与方之间都是通过网络进行通信的。由于网络本身的不稳定性,可能会造成分布式事务问题,因此在实现上,需要引人消息确认服务和消息恢复服务。
消息确认服务会定期检测事务发起方业务的执行状态和消息库中的数据,如果发现事务发起方业务的执行状态与消息库中的数据不一致,消息确认服务就会同步事务发起方的业务数据和消息库中的数据,保证数据一致性,确保事务发起方业务完成本地事务后消息定会发送成功。
消息恢复服务会定期检测事务参与方业务的执行状态和消息库中的数据,如果发现事务参与方业务的执行状态与消息库中的数据不一致(这里的不一致,通常指的是事务参与方消费消息后,执行本地事务操作失败,导致事务参与方本地事务的执行状态与消息库中的数据不一致),消息恢复服务就会恢复消息库中消息的状态,使消息的状态回滚为事务发起方发送消息成功,但未被事务参与方消费的状态。
方案的优缺点
消息最终一致性方案的可靠消息服务可以基于本地消息表和消息队列中间件两种方式实现
基于本地消息表实现的最终消息一致性方案
优点:
- 在业务应用中实现了消息的可靠性,减少了对消息中间件的依赖
缺点:
- 绑定了具体的业务场景,耦合度太高,不可公用和扩展
- 消息数据与业务数据同在一个数据库,占用了业务系统的资源
基于消息队列中间件实现的最终消息一致性方案
优点:
- 消息数据能够独立存储,与具体的业务数据库解耦
- 消息的并发性和吞吐量由于本地消息表方案
缺点:
- 发送一次消息需要完成两次网络交互,一次是消息的发送,另外一次是消息的提交或者回滚
- 需要实现消息的回查接口,增加了开发的成
需要注意的问题
使用可靠消息最终一致性方案解决分布式事务问题时,需要注意本地事务与消息发送的原子性问题、事务参与方接收消息的可靠性与幂等性问题
1、事务发送方本地事务与消息发送的原子性问题
- 产生的原因:可靠消息最终一致性要求事务发起方的本地事务与消息发送的操作具有原子性,也就是事务发起方执行本地事务成功后,一定要将消息发送出去,执行本地事务失败后,一定要丢弃消息。执行本地事务和发送消息,要么都成功,要么都失败
- 原子性问题的解决方案:在实际的解决方案中,可以通过消息确认服务解决本地事务与消息发送的原子性问题
2、事务参与方接收消息的可靠性问题
- 可靠性问题产生的原因:由于服务器宕机、服务崩溃或网络异常等原因,导致事务参与方不能正常接收消息或者接收消息后处理事务的过程中发生异常,无法将结果正确回传到消息库中。此时,就会产生可靠性问题
- 可靠性问题的解决方案:可以通过消息恢复服务保证事务参与方的可靠性
3、事务参与方接收消息的幂等性问题
- 幂等性问题产生的原因:在实际场景中,由于某种原因,可靠消息服务可能会多次向事务参与方发送消息,如果事务参与方的方法不具有幂等性,就会造成消息重复消费的问题,这就是典型的幂等性问题
- 幂等性问题的解方案:解快方案就是事务参与方的方法实现要具有幂等性,只要参数相同,无论调用多少次接口或方法、得出的结果都与第一次调用接口或方法得出的结果相同
最大努力通知型解决方案
当分布式事务跨越多个不同的系统,尤其是不同企业之间的系统时,解决分布式事务问题就需要用到最大努力通知型方案
适用的场景
最大努力通知型解决方案适用于最终一致性时间敏感度低的场景,并且事务被动方的处理结果不会影响主动方的处理结果,典型的使用场景就是支付成功后,支付平台异步通知商户支付结果
需要实现的服务模式
最大努力通知型解决方案需要实现的服务模式是可查询操作和幂等操作。例如,在充值业务场景中,用户调用支付服务充值成功后,支付服务会按照一定的阶梯型通知规则调用账户服务的接口,向账户服务发送支付数据。此时,账户服务的接口需要满足幂等性,这就是幂等操作。如果支付服务调用账户服务的接口超过了设置的最大次数,仍然没有调用成功,则支付服务需要提供查询支付结果的接口,以便账户服务调用并恢复丢失的业务
方案的执行流程
最大努力通知型分布式事务解决方案在执行的过程中,允许丢失消息,但需要业务主动方提供事务状态查询接口,以便业务被动方主动调用并恢复丢失的业务
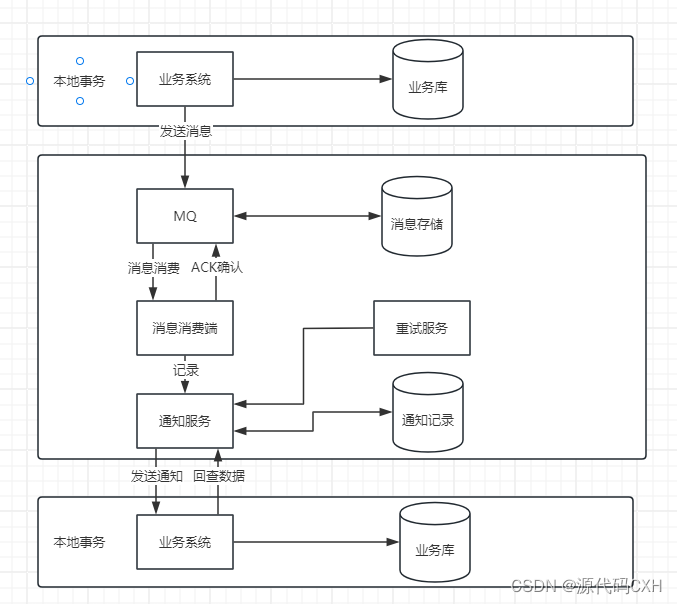
实现最大努力通知型方案时,需要实现如下功能。
- 业务主动方在完成业务处理后,会向业务被动方发送消息通知。发送消息通加时,允许消息丢失
- 在实现上,业务主动方可以设置时间阶梯型通知规则,在消息通知失败后,可以按照规则再次通知,直到到达最大通知次数为止
- 业务主动方需要提供查询接口供业务被动方按照需要查询,用于恢复丢失的消息
方案的优缺点
最大努力通知型方案存在如下优点:
- 能够实现跨企业的数据一致性。
- 业务被动方的处理结果不会影响业务主动方的处理结果
- 能够快速接入其他业务系统,达到业务数据一致性。
最大努力通知型方案存在如下缺点:
- 只适用于时间敏感度低的场景。
- 业务主动方发送的消息可能丢失,造成业务被动方收不到消息。
- 需要业务主动方提供查询消息的接口,业务被动方需要按照主动方的接口要求查数据,增加了开发成本
需要注意的问题
业务被动方需要保证接收通知的方法的幂等性,关键是要业务主动方通过一定的机最大限度地将业务的处理结果通知给业务被动方,因此必须解决如下两个问题
1、消息重复通知产生的问题:
- 消息重复通知产生的原因:由于业务主动方发送消息通知后,业务被动方不一定能够接收到消息,因此需要一定的阶梯型通知规则重复向业务被动方发送消息通知。此时,就出现了消息重复通情况,因为业务被动方的方法被执行了多次,所以有可能造成数据不一致的问题
- 消息重复通知的解决方案:保证业务被动方接收消息通知的方法具备幂等性,则在业务上就能够解决消息重影知的问题
2、消息通知丢失的问题
- 消息通知丢失问题的原因:如果业务主动方尽最大努力都没有将消息通知给业务被动方,或者业务被动方接收消息并执行完毕后,需要再次获取消息。此时,业务主动方已经删除对应的通知消息,向业务被动方发送消息通知,也就是说,消息通知已经丢失
- 消息通知丢失的解决方案:业务主动方需要提供查询消息的接口来满足业务被动方主动查询消息的需求,以恢复丢失的业务。另外,业务主动方在设计消息回查接口时,一定要注意接口的安全性和并发性
相关文章:

分布式事务解决方案(最终一致性【可靠消息解决方案】)
可靠消息最终一致性解决方案 可靠消息最终一致性分布式事务解决方案指的是事务的发起方执行完本地事务之后,发出一条消息,事务的参与方,也就是消息的消费者一定能够接收到这条消息并且处理完成,这个方案强调的是只要事务发起方将消…...
AI预测福彩3D采取888=3策略+和值012路一缩定乾坤测试5月28日预测第4弹
昨天的第二套方案已命中,第一套方案由于杀了对子,导致最终出错。 今天继续基于8883的大底,使用尽可能少的条件进行缩号,同时,同样准备两套方案,一套是我自己的条件进行缩号,另外一套是8883的大底…...
- 行为型模式(下))
JAVA:深入了解JAVA中的23种设计模式(三)- 行为型模式(下)
一、前言 在前三篇 《深入了解JAVA中的23种设计模式(一)- 创建型模式》 《深入了解JAVA中的23种设计模式(二)- 结构型模式》 《深入了解JAVA中的23种设计模式(三)- 行为型模式(上)》…...

微信小程序【WXML】
wxml wei xin markup language 类似于html 文档 数据绑定 小程序中使用{{}} 来进行数据绑定到模板中,如: wxml中的动态数据全部来自js中的data 简单绑定 //wxml <view> {{text }}</view>// index.js Page({data: {text: hello world}, })属性绑定…...

基于python实现的深度学习的车牌识别系统
基于python实现的深度学习的车牌识别系统 开发语言:Python 数据库:MySQL所用到的知识:Django框架工具:pycharm、Navicat、Maven 系统功能实现 登录页面 在车牌识别系统当中肯定是有登录的。怎么说呢,登录页面其实还是和最初的设…...
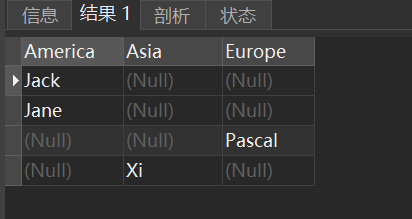
SQL试题使得每个学生 按照姓名的字⺟顺序依次排列 在对应的⼤洲下⾯
学⽣地理信息报告 学校有来⾃亚洲、欧洲和美洲的学⽣。 表countries 数据如下: namecontinentJaneAmericaPascalEuropeXiAsiaJackAmerica 1、编写解决⽅案实现对⼤洲(continent)列的 透视表 操作,使得每个学生 按照姓名的字⺟顺…...

kafka3.6.1版本学习
kafka目录结构 bin linux系统下可执行脚本文件 bin/windows windows系统下可执行脚本文件 config 配置文件 libs 依赖类库 licenses 许可信息 site-docs 文档 logs 服务日志 启动ZooKeeper 进入Kafka解压缩文件夹的config目录,修改zookeeper.properties配置文件 #t…...

移除链表元素-力扣
题目 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出:[1,2,3,4,5]示例 2: 输入&…...

HTTP请求拦截器链
文章目录 HTTP请求拦截器链需求定义写一个Controller方法接口写三个http请求拦截器把拦截器加入到配置中,并且配置拦截规则在postman里面发送请求,看下测试结果是否正确 HTTP请求拦截器链 需求定义 我们写一个包含三个HTTP请求拦截器的拦截器链&#x…...

再创佳绩丨达梦数据库一体机荣获2024数字中国创新大赛·信创赛道总决赛一等奖
5月24日,第七届数字中国建设峰会在福州盛大开幕,峰会内容安排包含开幕式、主论坛、分论坛、数字中国创新大赛、现场体验区及成果发布和专业工作会议等。武汉达梦数据库股份有限公司(以下简称达梦数据)受邀参加并在展、会、赛等多个环节深度参与。达梦全栈…...

数据分析之统计学基础
数据分析是现代企业和科研中不可或缺的一部分,而统计学是数据分析的基石。在本篇博客中,我们将介绍统计学的基础知识,涵盖数据类型、描述性统计(集中趋势、离散程度和偏差程度),并通过代码实例加以说明。 …...
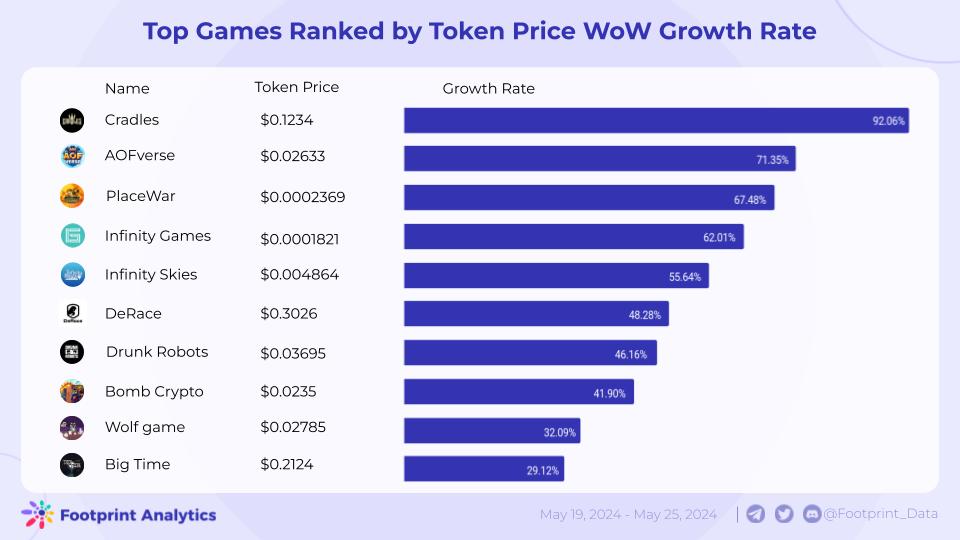
Web3 游戏周报(5.19 - 5.25)
【5.19 - 5.25】Web3 游戏行业动态: Arbitrum 已开启 “2 亿枚 ARB 游戏催化剂计划”的提案投票。 STEPN 在官方 X 宣布将推出全新社交健身应用 STEPN GO。 Oasys 正式推出《足球小将》漫改 Web3 游戏《Captain Tsubasa-RIVALS-》。 Gala Games :已销…...
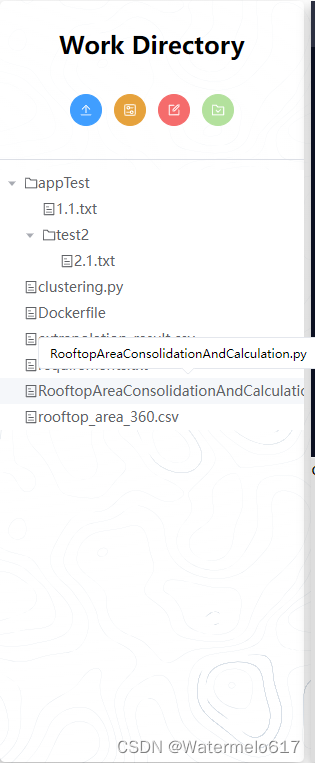
通过el-tree自定义渲染网页版工作目录,实现鼠标悬浮显示完整名称、用icon区分文件和文件夹等需求
目录 一、通过el-tree自定义渲染网页版工作目录 1.1、需求介绍 1.2、使用el-tree生成文档目录 1.2.1、官方基础用法 ①效果 ②代码: 1.2.2、自定义文档目录(实现鼠标悬浮显示完整名称、用icon区分文件和文件夹) ①效果(直接效…...
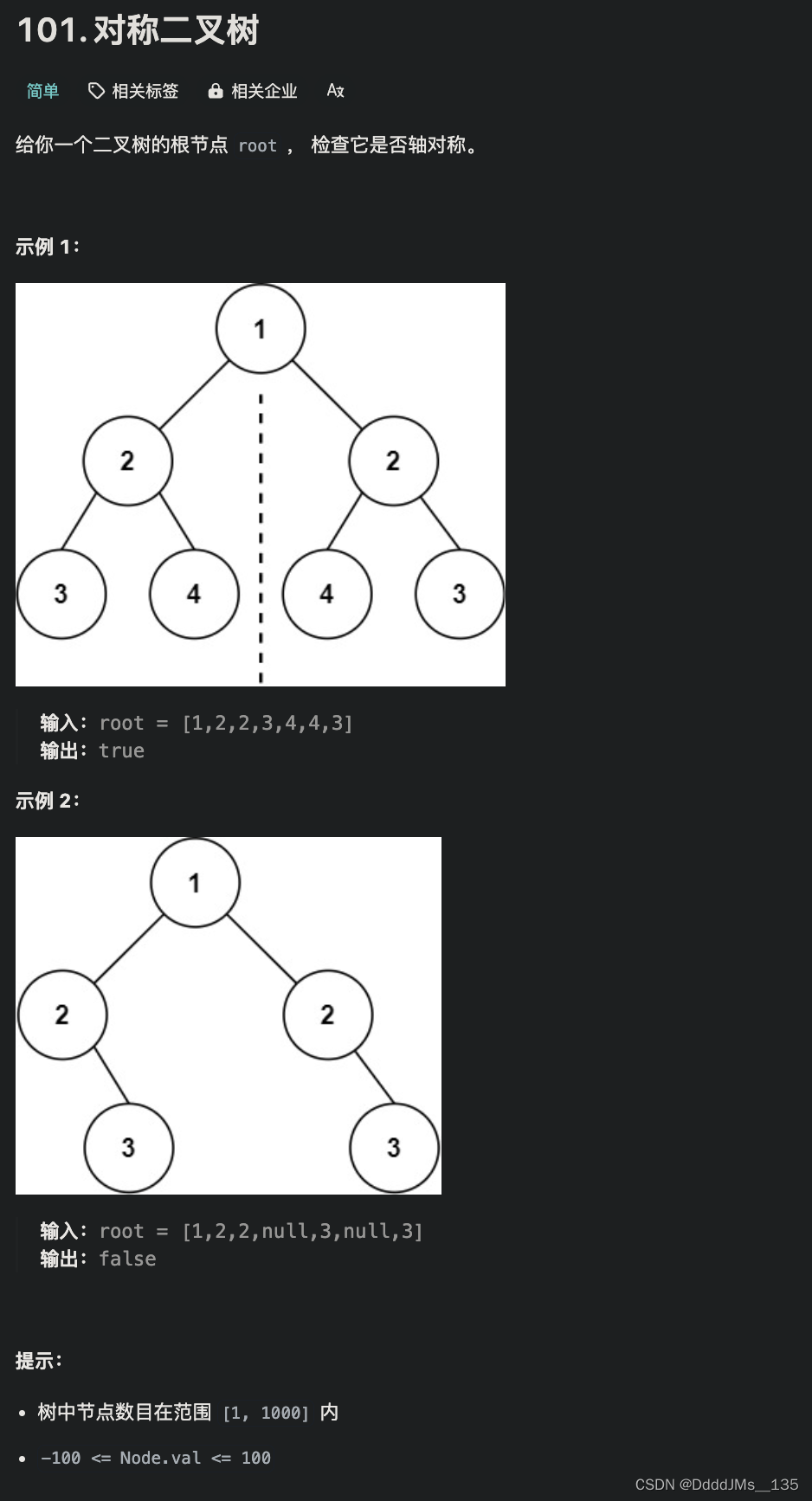
C语言 | Leetcode C语言题解之第101题对称二叉树
题目: 题解: /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool isSymmetric(struct TreeNode* root) {if (root NULL) return true;//如果根为空直接…...
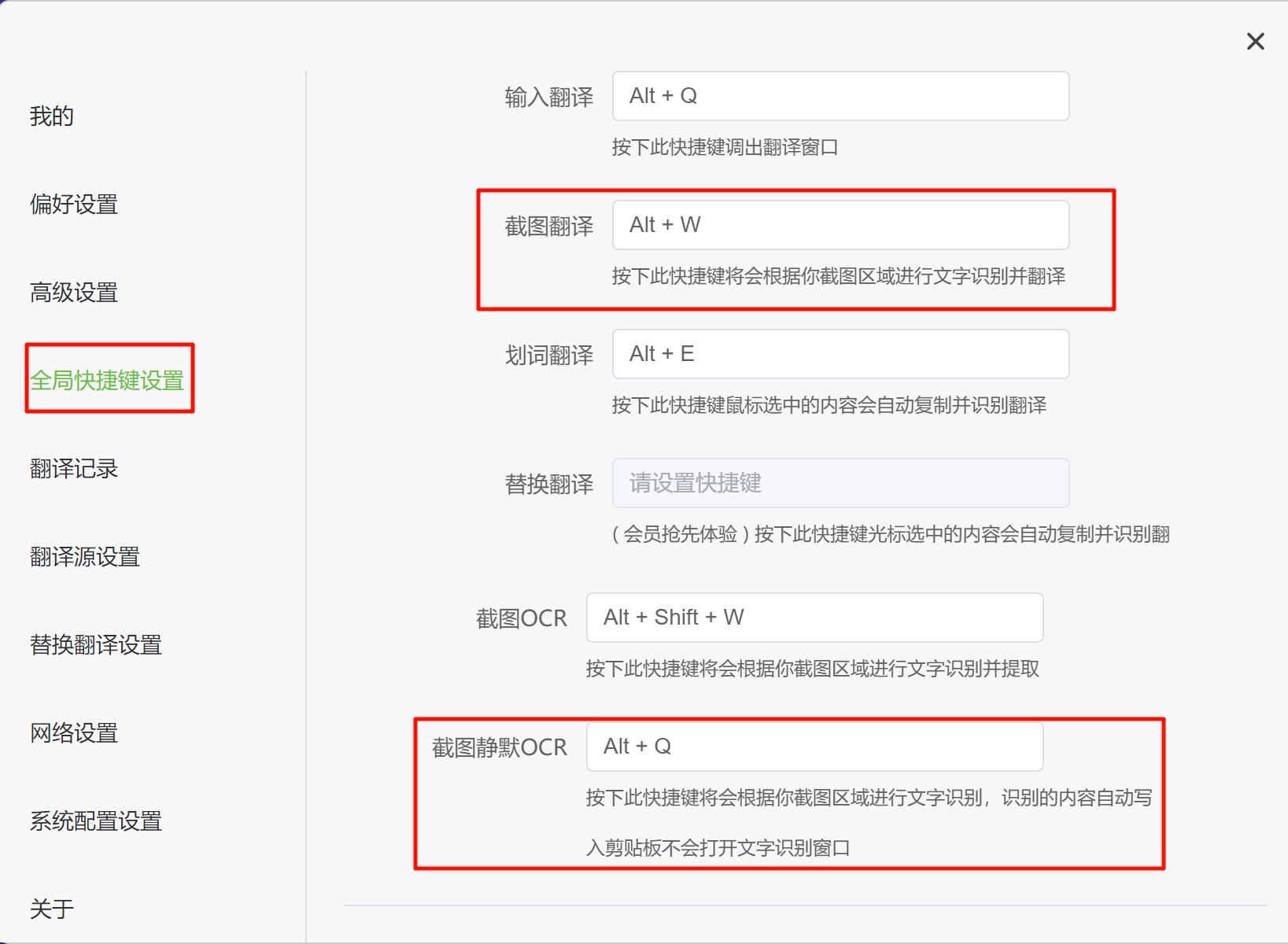
TTime:截图翻译/OCR
日常网页翻译Translate Web Pages完全足够,TTime最重要的功能,还是截图翻译,还有个厉害的功能,就是静默OCR,相比之前的分享的识字精灵效率更高。 软件使用 打开软件,点击翻译源设置,建议勾选一…...
【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突(C++两种方法模拟实现哈希表)(1)
🎉博主首页: 有趣的中国人 🎉专栏首页: C进阶 🎉其它专栏: C初阶 | Linux | 初阶数据结构 小伙伴们大家好,本片文章将会讲解 哈希函数与哈希 之 闭散列的线性探测解决哈希冲突 的相关内容。 如…...

四川农业大学Java实训项目圆满收官,汇智知了堂引领学子实践创新
近日,四川农业大学与汇智知了堂共同举办的Java实训项目正式迎来了项目汇报阶段。本次实训是汇智知了堂在高等教育领域深化校企合作、推动产教融合的一次重要实践,旨在为广大学子提供一个将理论知识与实际操作相结合的平台。 在实训过程中,汇…...

JavaScript的当前时间设置及Date的运算
作者:私语茶馆 1.场景描述 如下图,在HTML刚加载时,需要将开始时间设置为默认当前时间,结束时间设置为当前时间后7天的时间。手工填写时间时,时间段不超过30天。 这里涉及到两个技术点: 1)Input Date的当前时间设置 2)date的运算 由于是动态修改HTML,所以采用…...

网络安全管理制度
一、总则 目的:本制度旨在保障组织内部网络系统的安全、稳定运行,保护组织的信息资产不受损害,确保业务的连续性和数据的完整性。适用范围:本制度适用于组织内部所有使用网络系统的部门、员工及第三方合作伙伴。 二、网络安全管理…...

零基础,想做一名网络安全工程师,该怎么学习?
相比IT类的其它岗位,网络工程师的学习方向是比较明亮的。想要成为网络工程师,华为认证就是最好的学习方法。而网络工程师的从零开始学习就是从华为认证的初级开始学起,也就是HCIA,也就是从最基本的什么是IP地址、什么是交换机这…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
