强化学习学习笔记-李宏毅
Policy Gradient
- actor+env+reward function,env和reward是不能控制的,唯一可以变的是actor,Policy π \pi π是一个网络,参数为 θ \theta θ,输入是当前的观察,输出是采取的行为,例如游戏中输入的是游戏画面 s 1 s_1 s1,输出的是采取的操作 a 1 a_1 a1,有了决定的action a 1 a_1 a1之后会获取对应的reward r 1 r_1 r1,并且画面也会有对应的改变得到 s 2 s_2 s2,这个过程不断进行得到一个trajectory τ = { s 1 , a 1 , s 2 , a 2 , ⋯ , s T , a T } \tau = \{s_1,a_1,s_2,a_2,\cdots,s_T,a_T\} τ={s1,a1,s2,a2,⋯,sT,aT},假设网络参数固定,那么某条trajectory的几率是 p θ ( τ ) = p ( s 1 ) p θ ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) p θ ( a 2 ∣ s 2 ) ⋯ = p ( s 1 ) ∏ t = 1 T p θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) p_\theta(\tau) = p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)p_\theta(a_2|s_2)\cdots = p(s_1)\prod_{t = 1}^Tp_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t) pθ(τ)=p(s1)pθ(a1∣s1)p(s2∣s1,a1)pθ(a2∣s2)⋯=p(s1)∏t=1Tpθ(at∣st)p(st+1∣st,at),某一条trajectory得到的reward R ( τ ) = ∑ t = 1 T r t R(\tau)=\sum_{t = 1}^Tr_t R(τ)=∑t=1Trt,目标就是调整网络参数,使得reward的期望值大 R ‾ θ = ∑ τ R ( τ ) p θ ( τ ) \overline{R}_\theta = \sum_\tau R(\tau)p_\theta(\tau) Rθ=∑τR(τ)pθ(τ),如何优化 θ \theta θ呢,梯度下降 ∇ ( ‾ R ) θ = ∑ τ R ( τ ) ∇ p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ p θ ( τ ) p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ log p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ ) ] = 1 N ∑ n = 1 N R ( τ n ) ∇ log p θ ( τ n ) = 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n ) \nabla \overline(R)_\theta=\sum_\tau R(\tau)\nabla p_\theta(\tau) = \sum_\tau R(\tau)p_\theta(\tau)\frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}=\sum_\tau R(\tau)p_\theta(\tau)\nabla \log p_\theta(\tau) = E_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log p_\theta(\tau)] = \frac{1}{N}\sum_{n = 1}^NR(\tau^n)\nabla\log p_\theta(\tau^n) = \frac{1}{N}\sum_{n = 1}^N\sum_{t = 1}^{T_n}R(\tau^n)\nabla\log p_\theta(a^n_t|s_t^n) ∇(R)θ=∑τR(τ)∇pθ(τ)=∑τR(τ)pθ(τ)pθ(τ)∇pθ(τ)=∑τR(τ)pθ(τ)∇logpθ(τ)=Eτ∼pθ(τ)[R(τ)∇logpθ(τ)]=N1∑n=1NR(τn)∇logpθ(τn)=N1∑n=1N∑t=1TnR(τn)∇logpθ(atn∣stn),更新参数 θ ← θ + η ∇ R ‾ θ \theta\leftarrow \theta + \eta\nabla \overline{R}_\theta θ←θ+η∇Rθ,训练数据的获得,根据当前的网络,去玩游戏获取不同的trajectory,记录 s i t , a i t , r i s^t_i,a^t_i,r_i sit,ait,ri的数据对,计算梯度,更新参数,之后再次sample trajectory;
- 本质上可以看做一个分类问题,网络希望输入 s i t s_i^t sit输出 a i t a_i^t ait使得reward r i r_i ri最大,其中 r i r_i ri是针对整场游戏而言的,所以可以看做以reward为权重的log likelihood,希望加权的likelihood越大越好,以此提升输入 s i t s_i^t sit得到reward大的时候对应的 a i t a_i^t ait的几率,对应的就是分类的时候提升正确类别对应的几率;
- 由于训练的时候是sample,所以假设所有的reward都为正的时候可能会存在问题,所以reward整体都减去一个常量,可以取作reward的期望;
- 现在reward是trajectory粒度的,但是一条trajectory里面可能并不是所有的action都是好的,所以需要为不同的步骤分配不同的credit,此时变为 R ( τ n ) → ∑ t ′ = t T n r t ′ n → ∑ t ′ = t T n γ t ′ − t r t ′ n (随时间指数) R(\tau^n)\rightarrow \sum_{t'=t}^{T_n}r_{t'}^n\rightarrow\sum_{t'=t}^{T_n}\gamma^{t'-t}r_{t'}^n(随时间指数) R(τn)→∑t′=tTnrt′n→∑t′=tTnγt′−trt′n(随时间指数),减去bias之后记作 A θ ( s t , a t ) A^\theta(s_t,a_t) Aθ(st,at);
Proximal Policy Optimization
- On-policy:参与学习的agent和与环境互动的agent是同一个,上面的就是on-policy的做法,存在的问题就是更新了参数之后,之前sample出来的数据就不能再次使用了;
- Off-policy:参与学习的agent和与环境互动的agent不是同一个,希望使用sample出来的数据多次,使用从 π θ ′ \pi_{\theta'} πθ′中sample出来的数据来训练 π θ \pi_\theta πθ,其中 θ ′ \theta' θ′是固定的;
- importance sampling: E x ∼ p [ f ( x ) ] = 1 N ∑ i = 1 N f ( x i ) E_{x\sim p}[f(x)] = \frac{1}{N}\sum_{i = 1}^Nf(x^i) Ex∼p[f(x)]=N1∑i=1Nf(xi),但是我们现在不能从 p p p sample数据,只能从 q ( x ) q(x) q(x) sample数据,所以换成 E x ∼ p [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x = E x ∼ q [ f ( x ) p ( x ) q ( x ) ] E_{x\sim p}[f(x)] = \int f(x)p(x)dx = \int f(x)\frac{p(x)}{q(x)}q(x)dx = E_{x\sim q}[f(x)\frac{p(x)}{q(x)}] Ex∼p[f(x)]=∫f(x)p(x)dx=∫f(x)q(x)p(x)q(x)dx=Ex∼q[f(x)q(x)p(x)],也就是做了一个修正,乘上了 p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x),也就是importance weight,但是importance sampling有一个问题就是 p p p和 q q q不能差太多;
- 对应的梯度 ∇ R ‾ θ = E τ ∼ p θ ′ ( τ ) [ p θ ( τ ) p θ ′ ( τ ) R ( τ ) ∇ log p θ ( τ ) ] = E ( s t , a t ) ∼ π θ ′ [ P θ ( s t , a t ) P θ ′ ( s t , a t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t n ∣ s t n ) ] = E ( s t , a t ) ∼ π θ ′ [ P θ ( a t ∣ s t ) P θ ′ ( a t ∣ s t ) p θ ( s t ) p θ ′ ( s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t n ∣ s t n ) ] = E ( s t , a t ) ∼ π θ ′ [ P θ ( a t ∣ s t ) P θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t n ∣ s t n ) ] \nabla \overline R_\theta = E_{\tau\sim p_{\theta'}(\tau)}[\frac{p_\theta(\tau)}{p_{\theta'}(\tau)}R(\tau)\nabla\log p_\theta(\tau)]=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{P_\theta(s_t,a_t)}{P_{\theta'}(s_t,a_t)}A^{\theta'}(s_t,a_t)\nabla\log p_\theta(a_t^n|s_t^n)]=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{P_\theta(a_t|s_t)}{P_{\theta'}(a_t|s_t)}\frac{p_\theta(s_t)}{p_{\theta'}(s_t)}A^{\theta'}(s_t,a_t)\nabla\log p_\theta(a_t^n|s_t^n)]=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{P_\theta(a_t|s_t)}{P_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)\nabla\log p_\theta(a_t^n|s_t^n)] ∇Rθ=Eτ∼pθ′(τ)[pθ′(τ)pθ(τ)R(τ)∇logpθ(τ)]=E(st,at)∼πθ′[Pθ′(st,at)Pθ(st,at)Aθ′(st,at)∇logpθ(atn∣stn)]=E(st,at)∼πθ′[Pθ′(at∣st)Pθ(at∣st)pθ′(st)pθ(st)Aθ′(st,at)∇logpθ(atn∣stn)]=E(st,at)∼πθ′[Pθ′(at∣st)Pθ(at∣st)Aθ′(st,at)∇logpθ(atn∣stn)],根据 ∇ f ( x ) = f ( x ) ∇ log f ( x ) \nabla f(x) = f(x)\nabla\log f(x) ∇f(x)=f(x)∇logf(x)反推出原优化目标为 J θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ P θ ( a t ∣ s t ) P θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] J^{\theta'}(\theta) =E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{P_\theta(a_t|s_t)}{P_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)] Jθ′(θ)=E(st,at)∼πθ′[Pθ′(at∣st)Pθ(at∣st)Aθ′(st,at)];
- PPO就是加了一项使得 p θ p_\theta pθ和 p θ ′ p_{\theta'} pθ′之间不能差太多, J P P O θ ′ ( θ ) = J θ ′ ( θ ) − β K L ( θ , θ ′ ) J^{\theta'}_{PPO}(\theta) = J^{\theta'}(\theta)-\beta KL(\theta,\theta') JPPOθ′(θ)=Jθ′(θ)−βKL(θ,θ′),其中 β \beta β动态调整,如果 K L ( θ , θ ′ ) > K L m a x KL(\theta,\theta')>KL_{max} KL(θ,θ′)>KLmax增大 b e t a beta beta,如果 K L ( θ , θ ′ ) < K L m i n KL(\theta,\theta')<KL_{min} KL(θ,θ′)<KLmin减小 b e t a beta beta;
ref
https://www.youtube.com/watch?v=OAKAZhFmYoI&ab_channel=Hung-yiLee
相关文章:

强化学习学习笔记-李宏毅
Policy Gradient actorenvreward function,env和reward是不能控制的,唯一可以变的是actor,Policy π \pi π是一个网络,参数为 θ \theta θ,输入是当前的观察,输出是采取的行为,例如游戏中输…...
吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.8-3.9
目录 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter …...

SQL 语言:数据控制
文章目录 概述授权(GRANT)销权(REVOKE)总结 概述 SQL语言中的数据控制权限分配是数据库管理的重要组成部分,它涉及到如何合理地为用户分配对数据库资源的访问和使用权限。 权限类型:在SQL中,权限主要分为…...

『ZJUBCA Weekly Feed 07』MEV | AO超并行计算机 | Eigen layer AVS生态
一文读懂MEV:区块链的黑暗森林法则 01 💡TL;DR 这篇文章介绍了区块链中的最大可提取价值(MEV)概念,MEV 让矿工和验证者通过抢先交易、尾随交易和三明治攻击等手段获利,但也导致网络拥堵和交易费用增加。为了…...

正点原子延时函数delay_ms延时失效的原因
1、问题陈述 今天在测试小车程序的时候使用了如下代码,发现延时并没有达到期望的4s,而是仅仅延时了0.4s左右,本来以为少加了个0,最后在我多次测试下来,发现在延时大约超过2s的时候就会失效。 while(1){Set_Pwm(6000,60…...

MySQL 满足条件函数中使用查询最大值函数
在实际的数据库操作中,我们常常需要根据某些条件找到最大值并据此进行下一步的操作。例如,在一个包含订单信息的表中,可能需要找到特定客户的最大订单金额,并据此进行某些统计或决策。MySQL 提供了多种函数和查询方法,…...
Java | Leetcode Java题解之第101题对称二叉树
题目: 题解: class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}public boolean check(TreeNode u, TreeNode v) {Queue<TreeNode> q new LinkedList<TreeNode>();q.offer(u);q.offer(v);while (!q.…...

【区块链】智能合约漏洞测试
打开Ganache vscode打开智能合约漏洞工程 合约内容 pragma solidity >0.8.3;contract EtherStore {mapping(address > uint) public balances;function deposit() public payable {balances[msg.sender] msg.value;emit Balance(balances[msg.sender]);}function with…...
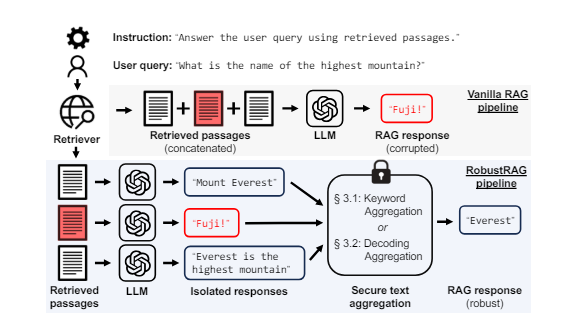
大模型主流 RAG 框架TOP10
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 总结链接…...
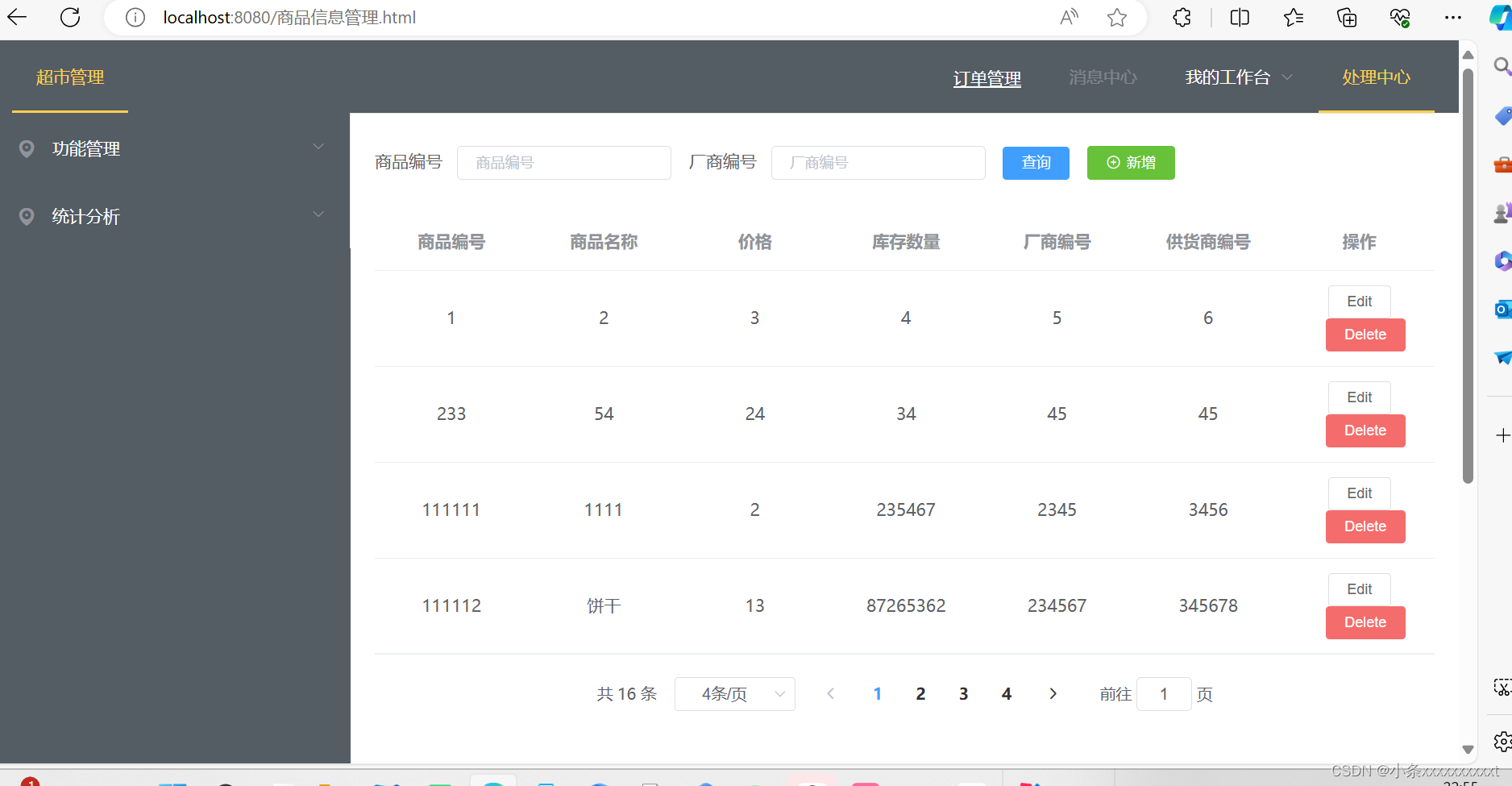
第八次javaweb作业
我们小组课程设计的题目是:超市管理系统,我认领的模块是:商品信息管理 controller package com.example.supermarker.controller;import com.example.supermarker.pojo.MerchInfo; import com.example.supermarker.pojo.PageBean; import c…...
)
js积累四 (读json文件)
function ReadRadioJson() {var url "../radio.json" //json文件url,本地的就写本地的位置,如果是服务器的就写服务器的路径var request new XMLHttpRequest();request.open("get", url, false); //设置请求方法与路径request.sen…...

关于我转生从零开始学C++这件事:升级Lv.25
❀❀❀ 文章由不准备秃的大伟原创 ❀❀❀ ♪♪♪ 若有转载,请联系博主哦~ ♪♪♪ ❤❤❤ 致力学好编程的宝藏博主,代码兴国!❤❤❤ OK了老铁们,又是一个周末,大伟又来继续给大家更新我们的C的内容了。那么根据上一篇博…...

mysql中text,longtext,mediumtext区别
文章目录 一.概览二、字节限制不同三、I/O 不同四、行迁移不同 一.概览 在 MySQL 中,text、mediumtext 和 longtext 都是用来存储大量文本数据的数据类型。 TEXT:TEXT 数据类型可以用来存储最大长度为 65,535(2^16-1)个字符的文本数据。如果存储的数据…...
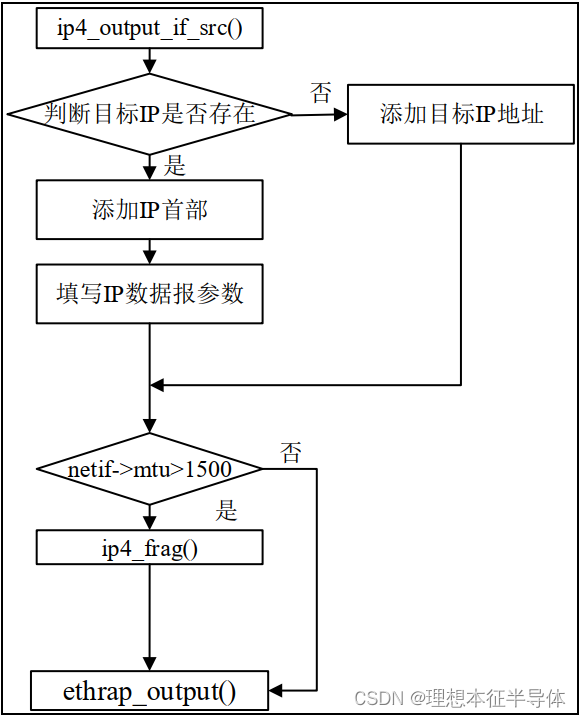
IP协议说明
文章目录 前言一、IP协议的简介二、IP数据报1.IP 数据报结构2.IP 数据报的分片解析3.IP 数据报的分片重装 三、IP 数据报的输出四、IP 数据报的输入 前言 IP 指网际互连协议, Internet Protocol 的缩写,是 TCP/IP 体系中的网络层协议。设计 IP 的目的是…...
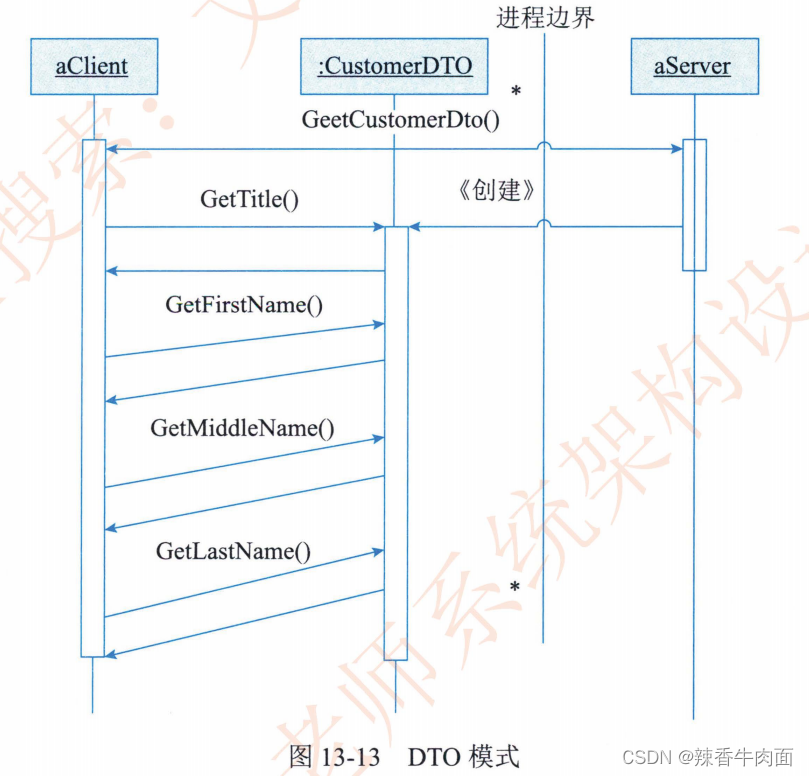
第13章 层次式架构设计理论与实践
层次式架构的核心思想是将系统组成为一种层次结构,每一层为上层服务,并作为下层客户。其实不管是分层还是其他的架构都是为了解耦,更好的复用,只要秉承着这种思想去理解一切都迎刃而解了。 13.1 层次上体系结构概述 回顾一下软件…...

FreeRtos进阶——消息队列的操作逻辑
消息队列(queue) 在不同的任务之间,如果我们需要互相之间通信,使用全局变量进行通信,是一种不安全的通信的方式。为保证线程安全,我们需要引入消息队列的通信方式。 粗暴的消息队列 为保证线程的安全&am…...

WordPress搭建流程
1. 简介 WordPress 是一个 PHP 编写的网站制作平台。WordPress 本身免费,并且拥有众多的主题可以使用,适合用于搭建个人博客、公司官网、独立站等。 2. 环境准备 2.1 WordPress 下载 WordPress 可以在 Worpress中文官网 下载(如果后续要将后台调成中文的话,一定要从中文…...

数据集004:跌倒检测数据集 (含数据集下载链接)
数据集简介: 该数据集为跌倒检测数据集,属于imageclassify任务,分为fall和nofall两大类,累计共1000张图片,均为人工标注 xml格式,可用于yolo训练。 数据集链接:跌倒检测数据集(1000…...

苹果与OpenAI合作在即:iOS 18中的ChatGPT引发期待与担忧
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

Android 逆向学习【2】——APK基本结构
APK安装在安卓机器上的,相当于就是windows的exe文件 APK实际上是个压缩包 只要是压缩的东西 .jar也是压缩包 里面是.class(java编译后的一些东西) APK是Android Package的缩写,即Android安装包。而apk文件其实就是一个压缩包,我们可以将apk文件的后…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
