AcWing 2568:树链剖分 ← 线段树+DFS
【题目来源】
https://www.acwing.com/problem/content/2570/
【题目描述】
给定一棵树,树中包含 n 个节点(编号 1∼n),其中第 i 个节点的权值为 ai。
初始时,1 号节点为树的根节点。
现在要对该树进行 m 次操作,操作分为以下 4 种类型:
● 1 u v k,修改路径上节点权值,将节点 u 和节点 v 之间路径上的所有节点(包括这两个节点)的权值增加 k。
● 2 u k,修改子树上节点权值,将以节点 u 为根的子树上的所有节点的权值增加 k。
● 3 u v,询问路径,询问节点 u 和节点 v 之间路径上的所有节点(包括这两个节点)的权值和。
● 4 u,询问子树,询问以节点 u 为根的子树上的所有节点的权值和。
【输入格式】
第一行包含一个整数 n,表示节点个数。
第二行包含 n 个整数,其中第 i 个整数表示 ai。
接下来 n−1 行,每行包含两个整数 x,y,表示节点 x 和节点 y 之间存在一条边。
再一行包含一个整数 m,表示操作次数。
接下来 m 行,每行包含一个操作,格式如题目所述。
【输出格式】
对于每个操作 3 和操作 4,输出一行一个整数表示答案。
【数据范围】
1≤n,m≤10^5,
0≤ai,k≤10^5,
1≤u,v,x,y≤n
【输入样例】
5
1 3 7 4 5
1 3
1 4
1 5
2 3
5
1 3 4 3
3 5 4
1 3 5 10
2 3 5
4 1
【输出样例】
16
69
【算法分析】
● 树链剖分
(1)树链剖分的核心思想,就是将树中任意一条路径拆分成 段的连续区间(或重链)。拆分后,树的所有操作都可转化为区间操作,且通常采用线段树进行维护。
(2)树链剖分的几个概念
重儿子/轻儿子:结点个数最多的子树的根结点称为当前结点的重儿子,其他子结点称为当前结点的轻儿子。若当前结点存在多个结点个数相同的子树,则任选一个子树的根结点作为当前结点的重儿子。故易知每个结点的重儿子是唯一的。
重边/轻边:重儿子与父结点之间的边,称为重边。其他边称为轻边。
重链:重边构成的极大路径,称为重链。
DFS序:深度优先遍历树的重儿子,可保证树中各条重链结点的编号是连续的。此性质保证了树链剖分后各区间是连续的。
(3)将一条路径拆分为重链的过程,类似于求最近公共祖先(LCA)。
【算法代码】
#include <bits/stdc++.h>
using namespace std;typedef long long LL;const int maxn=1e5+5;
const int maxm=maxn<<1;
int val[maxn],e[maxm],ne[maxm],h[maxn],idx;//id[]:dfn sequence number of the node
//nv[]:point weight of each dfs sequence number
int id[maxn],nv[maxn],tot;//cnt[]:number of child nodes, top[]:vertex of heavy chain
//son[]:heavy son, fa[]:parent node
int dep[maxn],cnt[maxn],top[maxn],fa[maxn],son[maxn];int n,m;struct SegmentTree {int le,ri;LL sum,lazy;
} tr[maxn<<2];void add(int a,int b) {e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void dfs1(int u,int father,int depth) { //dfs1:pretreatmentdep[u]=depth,fa[u]=father,cnt[u]=1;for(int i=h[u]; i!=-1; i=ne[i]) {int j=e[i];if(j==father) continue;dfs1(j,u,depth+1);cnt[u]+=cnt[j];if(cnt[son[u]]<cnt[j]) son[u]=j; //heavy son}
}void dfs2(int u,int vx) { //dfs2:split, t:vertex of heavy chainid[u]=++tot,nv[tot]=val[u],top[u]=vx;if(!son[u]) return; //leaf nodedfs2(son[u], vx); //Heavy son's heavy chain splitfor(int i=h[u]; i!=-1; i=ne[i]) { //handle light sonint j=e[i];if(j==fa[u] || j==son[u]) continue;dfs2(j,j); //The vertex of the light son's heavy chain is himself}
}/*------------ Content of segment tree ------------*/void pushup(int u) {tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}void pushdown(int u) {auto &rt=tr[u], &L=tr[u<<1], &R=tr[u<<1|1];if(rt.lazy) {L.sum+=rt.lazy*(L.ri-L.le+1);L.lazy+=rt.lazy;R.sum+=rt.lazy*(R.ri-R.le+1);R.lazy+=rt.lazy;rt.lazy=0;}
}void build(int u,int le,int ri) {tr[u]= {le,ri,nv[ri],0};if(le==ri) return;int mid=le+ri>>1;build(u<<1,le,mid), build(u<<1|1,mid+1,ri);pushup(u);
}void update(int u,int le,int ri,int k) {if(le<=tr[u].le && ri>=tr[u].ri) {tr[u].lazy+=k;tr[u].sum+=k*(tr[u].ri-tr[u].le+1);return;}pushdown(u);int mid=tr[u].le+tr[u].ri>>1;if(le<=mid) update(u<<1,le,ri,k);if(ri>mid) update(u<<1|1,le,ri,k);pushup(u);
}LL query(int u,int le,int ri) {if(le<=tr[u].le && ri>=tr[u].ri) return tr[u].sum;pushdown(u);int mid=(tr[u].le+tr[u].ri)>>1;LL res=0;if(le<=mid) res+=query(u<<1,le,ri);if(ri>mid) res+=query(u<<1|1,le,ri);return res;
}void update_path(int u,int v,int k) {while(top[u]!=top[v]) { //Climb up to find the same heavy chainif(dep[top[u]]<dep[top[v]]) swap(u,v);//Because of dfs order, the id of the upper node//must be smaller than that of the lower nodeupdate(1,id[top[u]],id[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);//In the same heavy chain, the remaining intervals are processedupdate(1,id[v],id[u],k);
}LL query_path(int u,int v) {LL res=0;while(top[u]!=top[v]) { //Climb up to find the same heavy chainif(dep[top[u]]<dep[top[v]]) swap(u,v);res+=query(1,id[top[u]],id[u]);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);//In the same heavy chain, the remaining intervals are processedres+=query(1,id[v],id[u]);return res;
}void update_tree(int u,int k) { //Add k to all the subtrees//Because of the order of dfs, the interval can be found directly//by the number of subtree nodesupdate(1,id[u],id[u]+cnt[u]-1,k);
}LL query_tree(int u) {//Because of the order of dfs, the interval can be found directly//by the number of subtree nodesreturn query(1,id[u],id[u]+cnt[u]-1);
}int main() {scanf("%d",&n);memset(h,-1,sizeof h);for(int i=1; i<=n; i++) scanf("%d",&val[i]);for(int i=1; i<n; i++) {int a,b;scanf("%d %d",&a,&b);add(a,b),add(b,a);}dfs1(1,-1,1);dfs2(1,1);build(1,1,n);scanf("%d",&m);while(m--) {int op,u,v,k;scanf("%d%d",&op,&u);if(op==1) {scanf("%d%d",&v,&k);update_path(u,v,k);} else if(op==2) {scanf("%d",&k);update_tree(u,k);} else if(op==3) {scanf("%d",&v);printf("%lld\n",query_path(u,v));} else printf("%lld\n",query_tree(u));}return 0;
}/*
in:
5
1 3 7 4 5
1 3
1 4
1 5
2 3
5
1 3 4 3
3 5 4
1 3 5 10
2 3 5
4 1out:
16
69
*/
【参考文献】
https://www.acwing.com/solution/content/62664/
https://www.acwing.com/problem/content/video/2570/
https://blog.csdn.net/qq_46105170/article/details/125497358
相关文章:
AcWing 2568:树链剖分 ← 线段树+DFS
【题目来源】https://www.acwing.com/problem/content/2570/【题目描述】 给定一棵树,树中包含 n 个节点(编号 1∼n),其中第 i 个节点的权值为 ai。 初始时,1 号节点为树的根节点。 现在要对该树进行 m 次操作…...
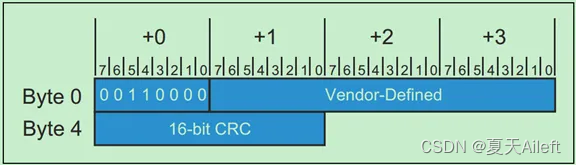
PCIe协议之-DLLP详解
✨前言: 🌟数据链路层的功能 数据链路层将从物理层中获得报文, 并将其传递给事务层; 同时接收事务层的报文, 并将其转发到物理层; 核心的功能有以下三点 1.保证TLP在 PCIe 链路中的正确传递; 2.数据链路层使用了容错…...
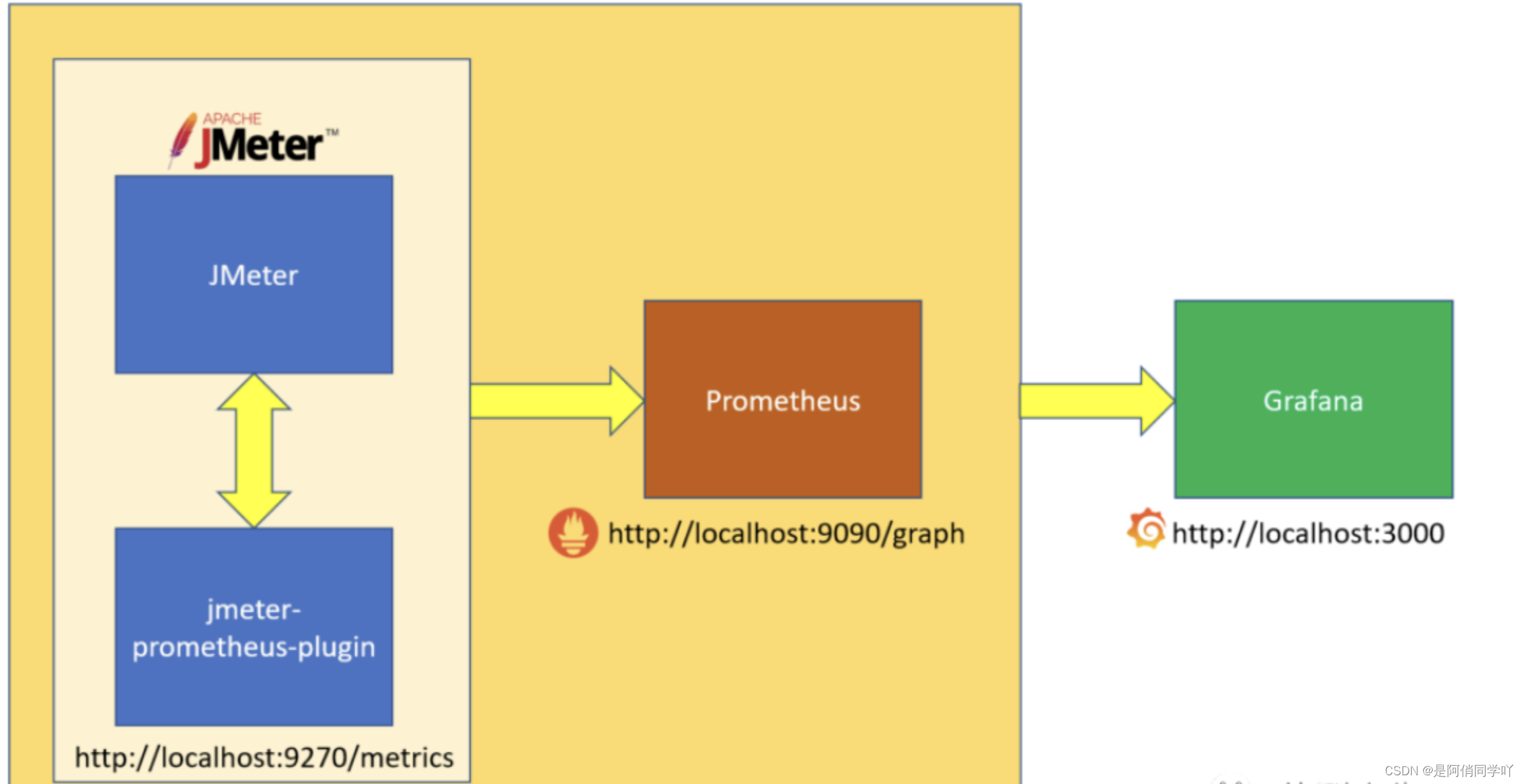
Jmeter+prometheus+grafana性能测试
文章目录 Jmeterprometheusgrafana性能测试背景目标设计思路原理案例启发 Jmeterprometheusgrafana性能测试 背景 在现代社会中,人们对于应用程序的响应速度和性能体验提出了越来越高的要求。无论是电子商务网站、社交媒体平台还是企业级软件系统,都…...
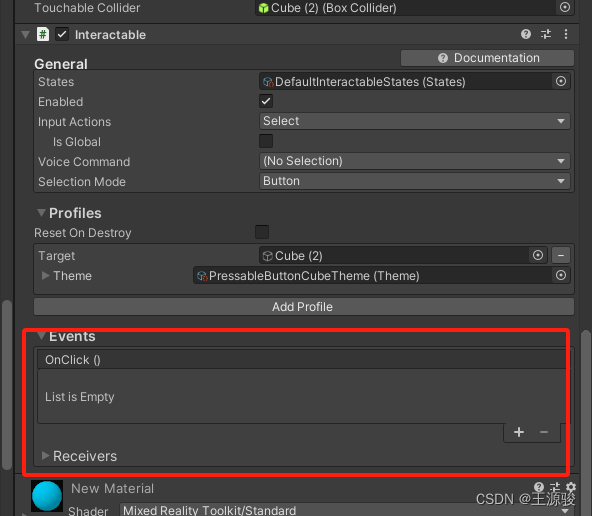
Hololens 2 新建自定义按钮
官方链接地址 1、创建Cube 2、添加PressableButton脚本,并点击AddNearin… 3、把Cube拖入到MovingButtonVisuals变量中 4、点击NearInteractionTouchable组件(这个组件是添加和上一个脚本绑定的,自动添加上来的)上的Fix… 5、…...

景源畅信:抖音小店新手小白如何做好运营?
在数字时代的浪潮中,抖音小店成为了众多创业者和商家的新宠。但面对激烈的市场竞争和不断变化的平台规则,新手小白如何才能在抖音小店的海洋里稳健航行,捕捉到属于自己的商机呢?接下来的内容将为你揭晓答案。 一、精准定位,明确目…...

力扣 42. 接雨水 python AC
双指针 class Solution:def trap(self, heights):l, r 0, len(heights) - 1maxl, maxr 0, 0ans 0while l < r:maxl, maxr max(maxl, heights[l]), max(maxr, heights[r])if maxl < maxr:ans maxl - heights[l]l 1else:ans maxr - heights[r]r - 1return ans单调栈…...

The 2022 ICPC Asia Nanjing Regional Contest - External D
G题 赛题补充 D题的题目来源 https://codeforces.com/gym/104128/problem/D 文章目录 题意思路代码 题意 给一个长度为n的数组,问对一段区间添加等差数列后的最大的第 k 大是多少 思路 通过观察题目可以发现答案的范围符合单调性,因此我们可以考虑二分…...

2024年蓝桥杯B组C++——复盘
1、握手问题 知识点:模拟 这道题很简单。但是不知道考试的时候有没有写错。一开始的43个人握手,仅需要两两握手,也就是从42个握手开始,而非43.很可惜。这道题没有拿稳这5分。也很有可能是这5分导致没有进决赛。 总结:…...
微调Llama3实现在线搜索引擎和RAG检索增强生成功能
视频中所出现的代码 Tavily SearchRAG 微调Llama3实现在线搜索引擎和RAG检索增强生成功能!打造自己的perplexity和GPTs!用PDF实现本地知识库_哔哩哔哩_bilibili 一.准备工作 1.安装环境 conda create --name unsloth_env python3.10 conda activate …...
【软件工程】【23.04】p1
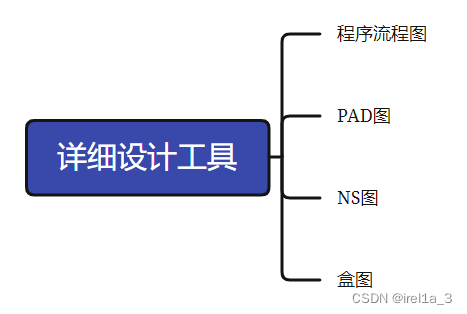
关键字: 软件模型、提炼、加工表达工具、通信内聚、访问依赖、边界类交互分析、RUP核心工作流、首先测试数据流、软件验证过程、CMMI过程域分类工程类; 软件工程目的、功能需求是需求的主体、结构化方法、耦合、详细设计工具、类、类图、RUP采用用例技…...

Flutter 中的 ColoredBox 小部件:全面指南
Flutter 中的 ColoredBox 小部件:全面指南 在 Flutter 的世界中,ColoredBox 是一个用于填充颜色的简单而强大的小部件。它是一个不透明的矩形,可以用来创建颜色块,作为布局的占位符,或者简单地改变某个区域的背景色。…...

【LeetCode 随笔】面试经典 150 题【中等+困难】持续更新中。。。
文章目录 12.【中等】整数转罗马数字151.【中等】反转字符串中的单词6.【中等】Z 字形变换68.【困难】文本左右对齐167.【中等】两数之和 II - 输入有序数组 🌈你好呀!我是 山顶风景独好 💝欢迎来到我的博客,很高兴能够在这里和您…...

SwiftUI中AppStorage的介绍使用
在Swift中,AppStorage是SwiftUI中引入的一个属性包装器,在这之前我们要存储一些轻量级的数据采用UserDefaults进行存取。而AppStorage用于从UserDefaults中读取值,当值改变时,它会自动重新调用视图的body属性。也就是说࿰…...
iCloud 照片到 Android 指南:帮助您快速将照片从 iCloud 传输到安卓手机
概括 iOS 和 Android 之间的传输是一个复杂的老问题。将 iCloud 照片传输到 Android 似乎是不可能的。放心。现在的高科技已经解决了这个问题。尽管 Apple 和 Android 不提供传输工具,但您仍然有其他有用的选项。这篇文章与您分享了 5 个技巧。因此,…...

知识点总结
1、Uboot的流程调用: 1.1、cmd_process函数是怎么被调用到的: cmd_process在common/command.c 1.2、uboot阶段断电,后续起不来,可能要换线去使用,也许和电源线有关 2、git 相关使用 2.1 .gitignore相关的使用 1、…...

Python并发与异步编程
Python的并发与异步编程是两个不同的概念,但它们经常一起使用,以提高程序的性能和响应能力。以下是对这两个概念的详细讲解: 并发编程 (Concurrency) 并发编程是指在程序中同时执行多个任务的能力。Python提供了几种实现并发的机制ÿ…...
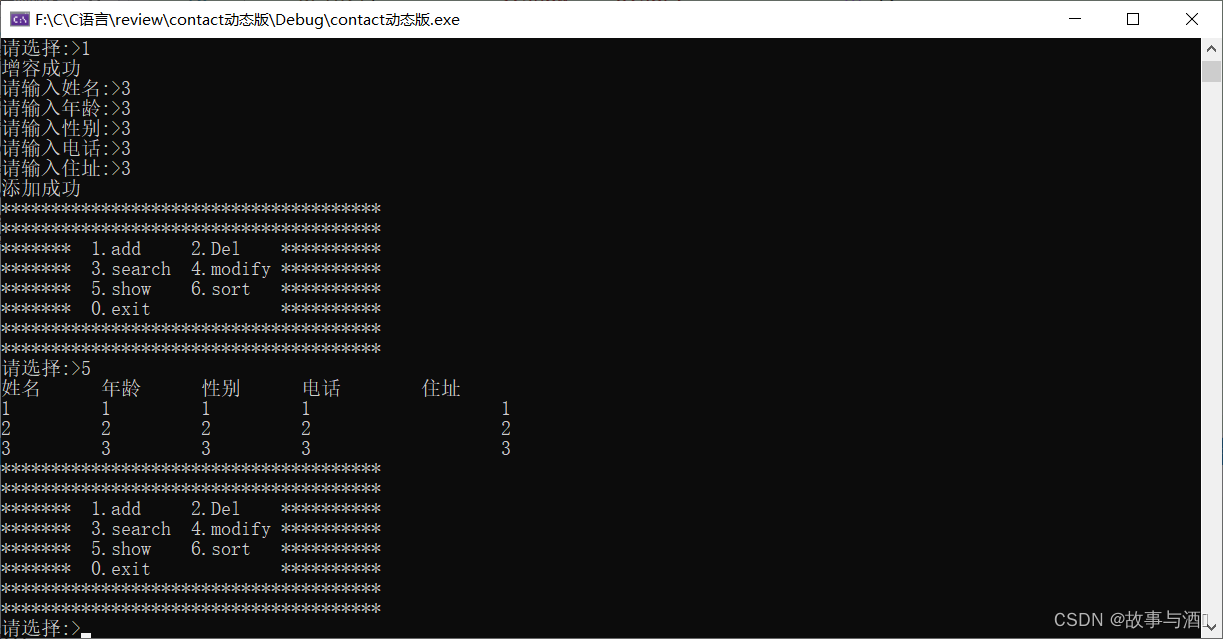
动态内存管理—C语言通讯录
目录 一,动态内存函数的介绍 1.1 malloc和free 1.2 calloc 1.3 realloc 1.4C/C程序的内存开辟 二,通讯录管理系统 动态内存函数的介绍 malloc free calloc realloc 一,动态内存函数的介绍 1.1 malloc和free void* malloc (…...
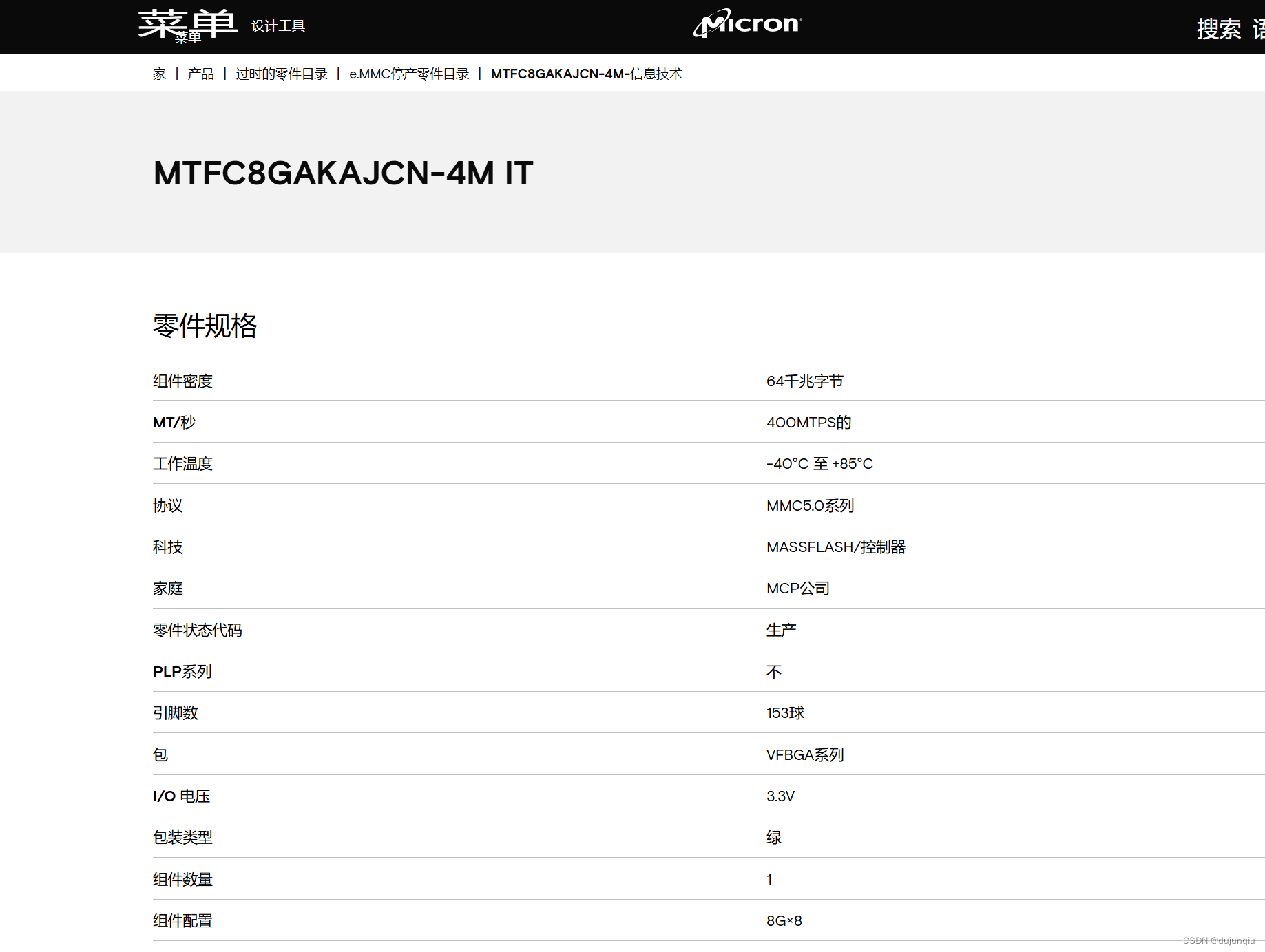
美光EMMC芯片丝印型号查询 8LK17/D9PSK, OXA17/JY997
问题说明 最近在使用美光EMMC的时候,发现通过芯片丝印查询不到 芯片的规格说明书; 经过查阅资料,发现美光的EMMC芯片 “由于空间限制,FBGA 封装组件具有与部件号不同的缩写部件标记”,需要通过官网查询丝印的FBGA cod…...

win32-鼠标消息、键盘消息、计时器消息、菜单资源
承接前文: win32窗口编程windows 开发基础win32-注册窗口类、创建窗口win32-显示窗口、消息循环、消息队列 本文目录 键盘消息键盘消息的分类WM_CHAR 字符消息 鼠标消息鼠标消息附带信息 定时器消息 WM_TIMER创建销毁定时器 菜单资源资源相关菜单资源使用命令消息的…...

springboot项目部署到linux服务器
springboot后端 修改前 修改后 vue前端 修改前 将地址中的 localhost改为 ip 重新生成war包 war上传到linux的tomcat的webapps下 其他环境配置和macOS大差不差 Tomcat安装使用与部署Web项目的三种方法_tomcat部署web项目-CSDN博客...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
