力扣hot100:23. 合并 K 个升序链表
23. 合并 K 个升序链表

这题非常容易想到归并排序的思路,俩升序序列合并,可以使用归并的方法。
不过这里显然是一个多路归并排序;包含多个子数组的归并算法,这可以让我们拓展归并算法的思路。
假设n是序列个数,ni是单个序列长度,length是单个序列最大长度
1、顺序单次归并
从左往右依次进行归并,但是这种方法存在一定的缺点。假设n是序列个数,ni是单个序列长度,根据题设,这个方法的最大比较次数至少是:
n 1 + ( n 1 + n 2 ) + ( n 1 + n 2 + n 3 ) ⋅ ⋅ ⋅ = n ∗ n 1 + ( n − 1 ) ∗ n 2 + ( n − 2 ) ∗ n 3 ⋅ ⋅ ⋅ < = n ∗ ( n 1 + n 2 + n 3 + ⋅ ⋅ ⋅ ) = n 2 ∗ l e n g t h < = 1 0 4 ∗ 500 ∗ 1 0 4 n1+(n1+n2)+(n1+n2+n3)··· = n*n1 + (n-1)*n2 + (n-2)*n3··· <= n*(n1+n2+n3+···) = n^2 * length <=10^4*500*10^4 n1+(n1+n2)+(n1+n2+n3)⋅⋅⋅=n∗n1+(n−1)∗n2+(n−2)∗n3⋅⋅⋅<=n∗(n1+n2+n3+⋅⋅⋅)=n2∗length<=104∗500∗104
这相当于每个序列都需要被比较序列个数次,这换成是多路归并的数组合并也是一样的。
官方:

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode * head = nullptr;for(int i = lists.size() - 1;i >= 0; --i){head = merge(head, lists[i]);ListNode * temp = head;}return head;}
private:ListNode * merge(ListNode * p,ListNode * q){if(!p) return q;if(!q) return p;ListNode * head = p;if(head->val > q->val) head = q;if(head == p) p = p->next;else q = q->next;ListNode * temp = head;while(p && q){if(p->val > q->val){head->next = q;q = q->next;}else{head->next = p;p = p->next;}head = head->next;}head->next = p ? p : q;return temp;}
};
2、分治归并
使用分治的思想排序是很容易想到的,但是不能很容易的知道分治归并速度一定更快,接下来让我详细思考一下是否会更快:
我们可以考虑,每次将序列数量减半合并,那么每一层合并使用的时间是 O ( l e n g t h ∗ n ) O(length*n) O(length∗n),我们知道每层数量减半,那么一共是有 O ( l o g n ) O(logn) O(logn)层,所以时间复杂度为 O ( n l o g n ∗ l e n g t h ) O(nlogn * length) O(nlogn∗length)
为什么分治归并会比普通顺次归并要快?
可以这样看一下,使用分治,将所有数分为两个区间[l,mid]和[mid+1,r],左区间的数 和 右区间的数只会在最后合并时比较一次,其他时候打死不相往来。而使用顺序归并,左区间的数 和 右区间的数会比较很多次,在考虑到


class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {if(lists.size() == 0) return nullptr;return mergesort(lists, 0, lists.size() - 1);}
private:ListNode * merge(ListNode * p,ListNode * q){if(!p) return q;if(!q) return p;ListNode * head = p;if(head->val > q->val) head = q;if(head == p) p = p->next;else q = q->next;ListNode * temp = head;while(p && q){if(p->val > q->val){head->next = q;q = q->next;}else{head->next = p;p = p->next;}head = head->next;}head->next = p ? p : q;return temp;}ListNode * mergesort(vector<ListNode*>& lists,int left,int right){if(left == right) return lists[left];int mid = (left + right) >> 1;ListNode * p = mergesort(lists,left,mid);ListNode * q = mergesort(lists,mid + 1, right);return merge(p, q);}
};
3、使用优先队列合并
这种方式非常牛。
我们将所有序列,依据序列头部的元素大小放入一个优先队列,那么这个优先队列的深度是 l o g n logn logn,然而我们每次取出一个结点它的头部必然是现在里面最小的,将它放入待合并的目标序列中,然后将该序列后移一位,插入到优先队列中。因此每个元素插入时间是 O ( l o g n ) O(logn) O(logn),一共有 ( l e n g t h ∗ n ) (length * n) (length∗n)个元素。所以总时间为 O ( n l o g n ∗ l e n g t h ) O(nlogn*length) O(nlogn∗length)

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {if(lists.size() == 0) return nullptr;priority_queue<ListNode *,vector<ListNode *>,Sort> q;for(int i = lists.size() - 1;i >= 0; --i) if(lists[i]) q.push(lists[i]);ListNode * dummy = new ListNode;ListNode * temp = dummy;while(!q.empty()){ListNode * head = q.top();q.pop();temp->next = head;temp = temp->next;head = head->next;if(head) q.push(head);}temp = dummy->next;delete dummy;return temp;}
private:struct Sort{bool operator ()(const ListNode * a,const ListNode * b){return a->val > b->val;}};
};
能够实现优先队列,那么这个问题就很容易被解决。
- 我们需要注意两个问题
- 优先队列使用的比较函数必须自定义为结构体或者符号重载
- 优先队列使用的比较函数的大于号小于号取值,和sort刚好相反。
使用方式:
priority_queue<Exp,vector<Exp>,cmp> q;
struct cmp{bool operator() (Exp a, Exp b){if() return true;return false;}
}
唯一变化的就是括号里面的类型Exp和你想要定义的比较方式。
相关文章:

力扣hot100:23. 合并 K 个升序链表
23. 合并 K 个升序链表 这题非常容易想到归并排序的思路,俩升序序列合并,可以使用归并的方法。 不过这里显然是一个多路归并排序;包含多个子数组的归并算法,这可以让我们拓展归并算法的思路。 假设n是序列个数,ni是…...
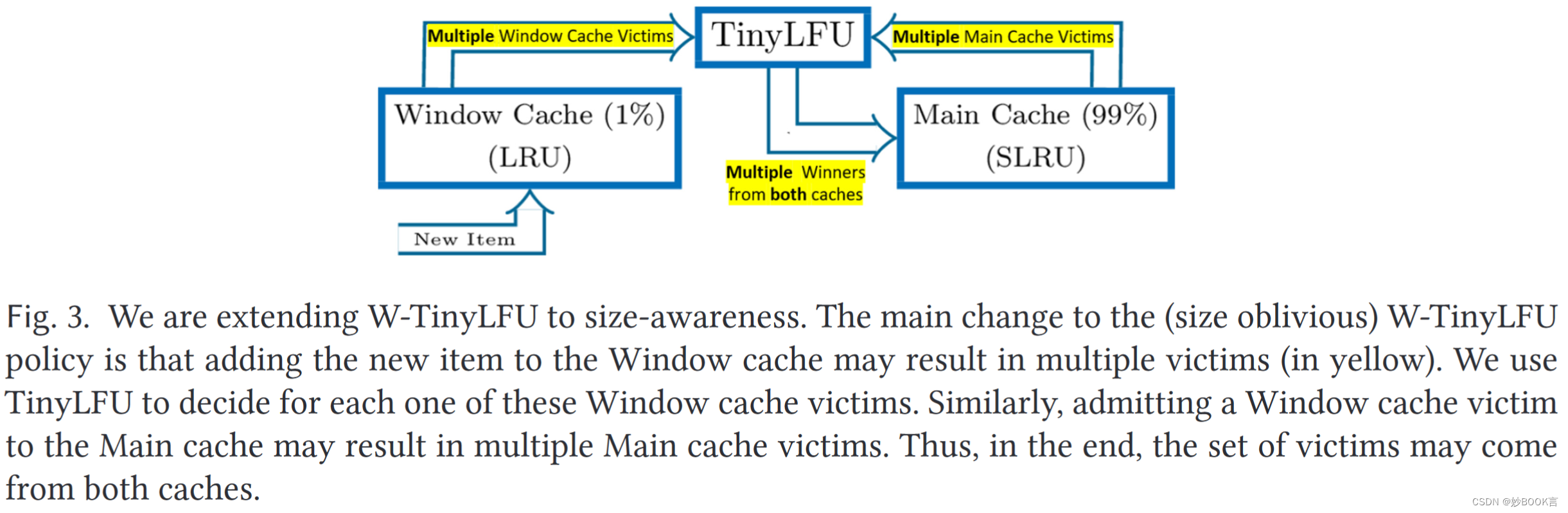
Lightweight Robust Size Aware Cache Management——论文泛读
TOC 2022 Paper 论文阅读笔记整理 问题 现代键值存储、对象存储、互联网代理缓存和内容交付网络(CDN)通常管理不同大小的对象,例如,Blob、不同长度的视频文件、不同分辨率的图像和小文件。在这种工作负载中,大小感知…...
搜索自动补全-elasticsearch实现
1. elasticsearch准备 1.1 拼音分词器 github地址:https://github.com/infinilabs/analysis-pinyin/releases?page6 必须与elasticsearch的版本相同 第四步,重启es docker restart es1.2 定义索引库 PUT /app_info_article {"settings": …...

连接远程的kafka【linux】
# 连接远程的kafka【linux】 前言版权推荐连接远程的kafka【linux】一、开放防火墙端口二、本地测试是否能访问端口三、远程kafka配置四、开启远程kakfa五、本地测试能否连接远程六、SpringBoot测试连接 遇到的问题最后 前言 2024-5-14 18:45:48 以下内容源自《【linux】》 仅…...
简单的 Cython 示例
1, pyx文件 fibonacci.pyx def fibonacci_old(n):if n < 0:return 0elif n 1:return 1else:return fibonacci_old(n-1) fibonacci_old(n-2) 2,setup.py setup.py from setuptools import setup from Cython.Build import cythonizesetup(ext_mod…...

Laravel时间处理类Carbon
时间和日期处理是非常常见的任务。Carbon 是一个功能强大的 PHP 扩展包,它为我们提供了许多方便的方法来处理日期和时间。在 Laravel 中,你无需单独安装 Carbon,因为 Laravel 默认已经包含了它。如果你正在使用 Laravel,那么你已经…...

2024年5月软考架构题目回忆分享
十年架构两茫茫 ,Redis , UML 夜来幽梦忽还乡 , 大数据, Lambda 选择题 1.需求分析和架构设计面临这两个不同对象,一个是问题空间,一个是解空间 这是英文题,总共五个题目,只记得这么多 2. …...

香橙派 AIpro开发板初上手
一、香橙派 AIpro开箱 最近拿到了香橙派 AIpro(OrangePi AIpro),下面就是里面的板子和相关的配件。包含主板、散热组件、电源适配器、双C口电源线、32GB SD卡。我手上的这个是8G LPDDR4X运存的版本。 OrangePi AIpro开发板是一款由香橙派与华…...

如何使用DotNet-MetaData识别.NET恶意软件源码文件元数据
关于DotNet-MetaData DotNet-MetaData是一款针对.NET恶意软件的安全分析工具,该工具专为蓝队研究人员设计,可以帮助广大研究人员轻松识别.NET恶意软件二进制源代码文件中的元数据。 工具架构 当前版本的DotNet-MetaData主要由以下两个部分组成…...

LeetCode---栈与队列
232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int pee…...

【教程】利用API接口添加本站同款【每日新闻早早报】-每天自动更新,不占用文章数量
本次分享的是给网站添加一个每日早报的文章,可以看到本站置顶上面还有一个日更的日报,这是利用ALAPI的接口完成的!利用接口有利也有弊,因为每次用户访问网站的时候就会增加一次API接口请求,导致文章的请求会因为请求量…...

僵尸进程,孤儿进程,守护进程
【一】僵尸进程 1.僵尸进程是指完成自己的任务之后,没有被父进程回收资源,占用系统资源,对计算机有害,应该避免 """ 所有的子进程在运行结束之后都会变成僵尸进程(死了没死透)还保留着pid和一些运行过程的中的记录便于主进程查看(短时间…...
Nuxt3 中使用 ESLint
# 快速安装 使用该命令安装的同时会给依赖、内置模块同时更新 npx nuxi module add eslint安装完毕后,nuxt.config.ts 文件 和 package.json 文件 会新增代码段: # nuxt.config.ts modules: ["nuxt/eslint" ] # package.json "devDep…...
【Jmeter】性能测试之压测脚本生成,也可以录制接口自动化测试场景
准备工作-10分中药录制HTTPS脚本,需配置证书 准备工作-10分中药 以https://www.baidu.com/这个地址为录制脚本的示例。 录制脚本前的准备工作当然是得先把Jmeter下载安装好、JDK环境配置好、打开Jmeter.bat,打开cmd,输入ipconfig,…...
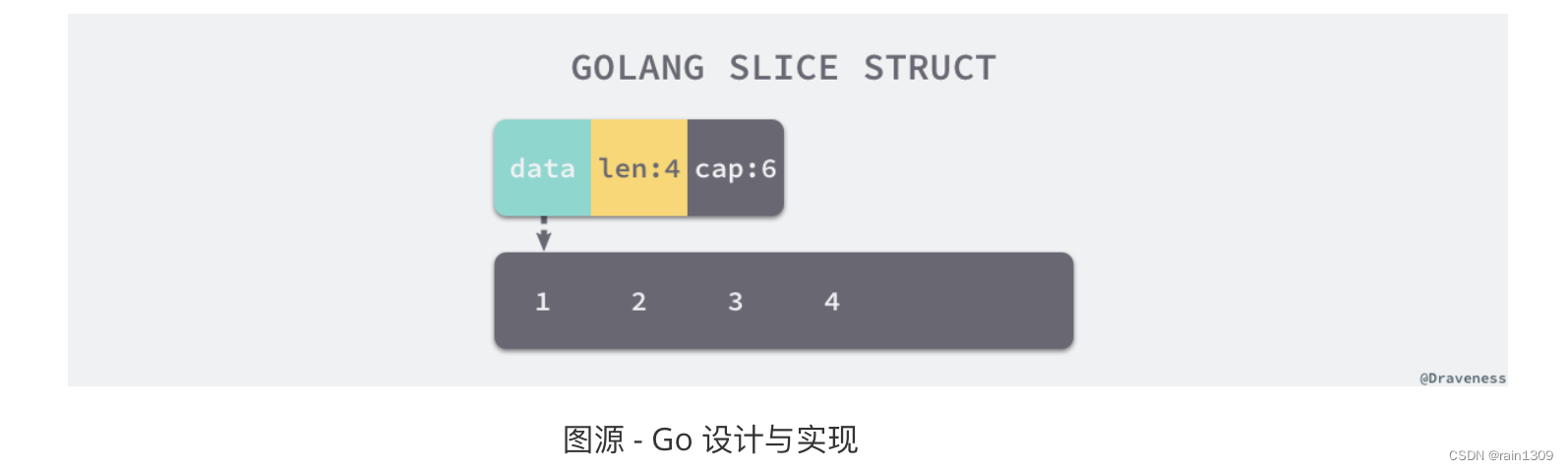
Go 编程技巧:零拷贝字符串与切片转换的高效秘籍
前言 在深入探讨Go语言中字符串与切片类型转换的高效方法之前,让我们先思考一个关键问题:如何在不进行内存拷贝的情况下,实现这两种数据类型之间的无缝转换?本文将详细解析Go语言中字符串(字符类型)和切…...

音视频开发—FFmpeg 音频重采样详解
音频重采样(audio resampling)是指改变音频信号的采样率的过程。采样率(sample rate)是指每秒钟采集的音频样本数,通常以赫兹(Hz)或每秒样本数(samples per second)表示。…...

统计本地端口占用情况
要查看MongoDB是否正在备份,可以通过以下几种方法: 查看MongoDB的进程列表: 使用命令ps -ef | grep mongo,这将列出所有正在运行的MongoDB进程。在输出的列表中,你可以查看是否有与备份相关的进程或任务正在运行。 查…...
-查询优化(9)-外部联接优化)
【MySQL精通之路】SQL优化(1)-查询优化(9)-外部联接优化
主博客: 【MySQL精通之路】SQL优化(1)-查询优化-CSDN博客 上一篇: 【MySQL精通之路】SQL优化(1)-查询优化(8)-嵌套联接优化-CSDN博客 下一篇: 【MySQL精通之路】SQL优化(1)-查询优化(10)-外部联接简化-CSDN博客 外部联接包括LEFT JOIN和…...

Python应用开发——30天学习Streamlit Python包进行APP的构建(1)
关于 #30天学Streamlit #30天学Streamlit 是一个旨在帮助你学习构建 Streamlit 应用的编程挑战。 你将学会: 如何搭建一个编程环境用于构建 Streamlit 应用构建你的第一个 Streamlit 应用学习所有好玩的、能用在 Streamlit 应用里的输入输出组件🗓️ 天 1 设置本地开发环境…...
轻兔推荐 —— 一个好用的软件服务推荐平台
给大家推荐一个好用的的软件服务推荐平台:轻兔推荐 网站界面简洁大方,没有太多杂七杂八的功能和页面,有明暗主题色可以选择,默认为亮色,可在网站上方手动切换。 每工作日都会推荐一款软件,有时会加更&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
