数据结构 | 详解二叉树——堆与堆排序
🥝堆
大堆:父节点总是大于子节点。
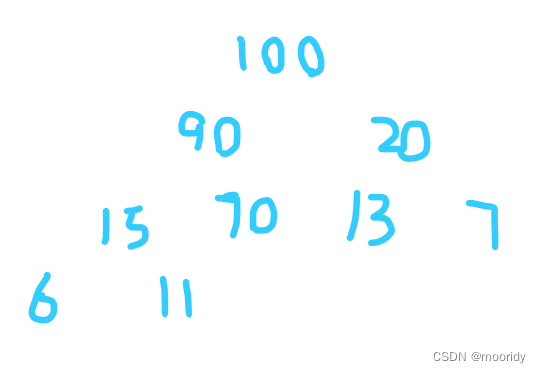
小堆:父节点总是小于子节点。
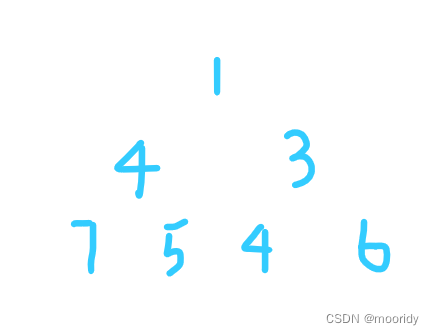
注意:1.同一个节点下的两个子节点并无要求先后顺序。
2.堆可以是无序的。
🍉堆的实现
🌴深度剖析
1.父节点和子节点之间的关系
子节点=(父节点*2)+1
或者子节点=(父节点*2)+2
父节点=(子节点-1)/2
2.堆的插入HeapPush实现
void HeapPush(Heap* php, HPDataType x) {assert(php);if (php->size == php->capacity) {int newcapacity = 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("malloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;AdjustUp(php->a,php->size);php->size++;
}3.堆的删除HeapPop函数的实现
函数目的:删除堆顶元素
为了避免破坏堆的整体结构,先将首尾元素进行交换,再对首元素进行向下调整,直到满足堆。最后php->size--即可删除原栈顶元素。
void HeapPop(Heap* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);AdjustDown(php->a, php->size,0);php->size--;
}
🥳代码实现
Heap.h
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* php);
// 堆的插入
void HeapPush(Heap* php, HPDataType x);
// 堆的删除
void HeapPop(Heap* php);
// 取堆顶的数据
HPDataType HeapTop(Heap* php);
// 堆的数据个数
int HeapSize(Heap* php);
// 堆的判空
int HeapEmpty(Heap* php);
Heap.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
void HeapInit(Heap* php) {assert(php);php->a = NULL;php->capacity = php->size = 0;
}void HeapDestory(Heap* php) {assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}void swap(int* a, int* b) {int tmp = *a;*a= *b;*b = tmp;
}
//小堆
void AdjustUp(HPDataType* a,int child) {assert(a);int parent = (child - 1) / 2;while (child > 0) {if (a[parent] > a[child]) {swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}void HeapPush(Heap* php, HPDataType x) {assert(php);if (php->size == php->capacity) {int newcapacity = 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("malloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;AdjustUp(php->a,php->size);php->size++;
}
//从给定的子节点开始,不断向上与其父节点进行比较和可能的交换,直到达到根节点或找到一个满足最大堆性质的父节点为止。
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child] < a[child + 1]) {child++;}if (a[parent] < a[child]) {swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);AdjustDown(php->a, php->size,0);php->size--;
}HPDataType HeapTop(Heap* php) {assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(Heap* php) {assert(php);return php->size;
}int HeapEmpty(Heap* php) {assert(php);return php->size;
}test.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
int main() {Heap hp;HeapInit(&hp);HeapPush(&hp, 7);HeapPush(&hp, 6);HeapPush(&hp, 5);HeapPush(&hp, 4);HeapPush(&hp, 3);HeapPush(&hp, 2);HeapPush(&hp, 1);for (int i = 0; i < hp.size; i++) {printf("%d ", hp.a[i]);}HeapPop(&hp);printf("\n");for (int i = 0; i < hp.size; i++) {printf("%d ", hp.a[i]);}printf("\n");printf("堆顶元素为%d\n", HeapTop(&hp));if (HeapEmpty(&hp)) {printf("堆不为空\n");}else {printf("堆为空\n");}return 0;
}🍇堆排序
🌴深度剖析
第一步:建堆
(升序建大堆,降序建小堆)
以升序为例:
从最后一个父节点开始向前遍历,向上调整(大的上小的下)。
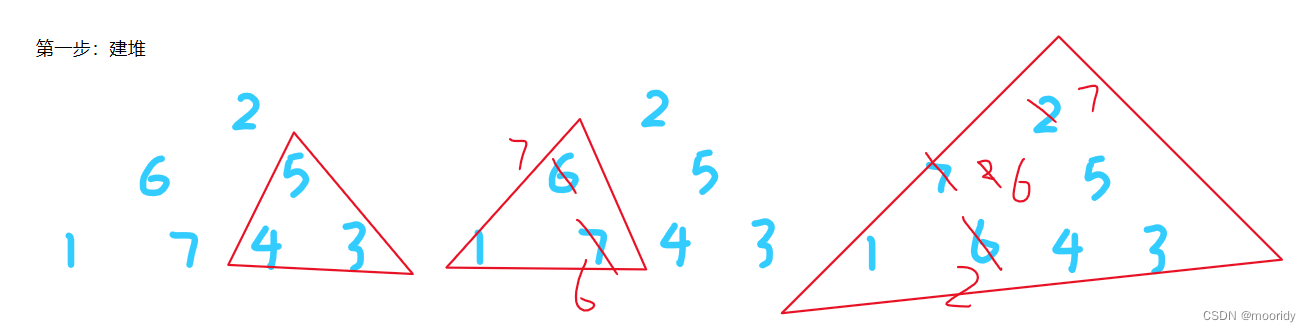
//建堆:从倒数第一个父节点开始向前遍历,向下调整for (int i = (n-1-1)/2; i >=0 ;i--) {AdjustDown(a,n,i);}第二步:排序
1.首尾元素交换(左图)
2.再向下调整(大的上小的下),这样调整后的堆顶元素必为调整范围内的最大值,经过下一轮的首尾元素交换后,就可以放入调整完的区域内。
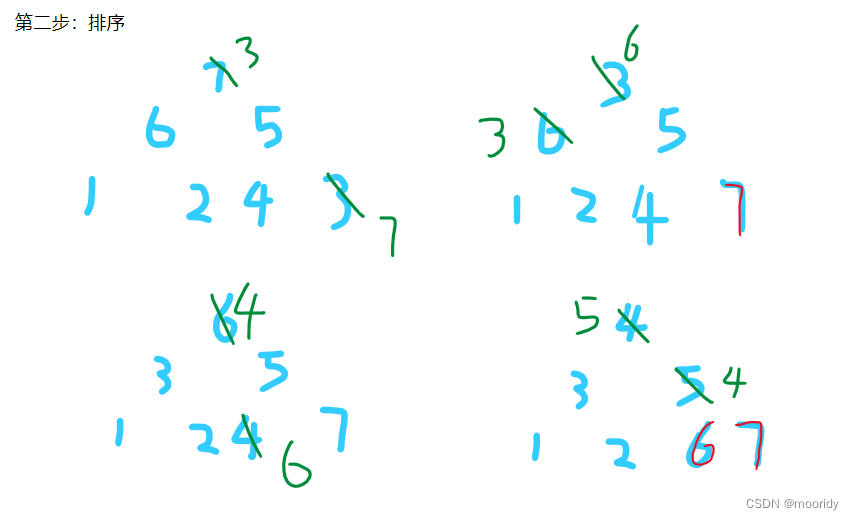

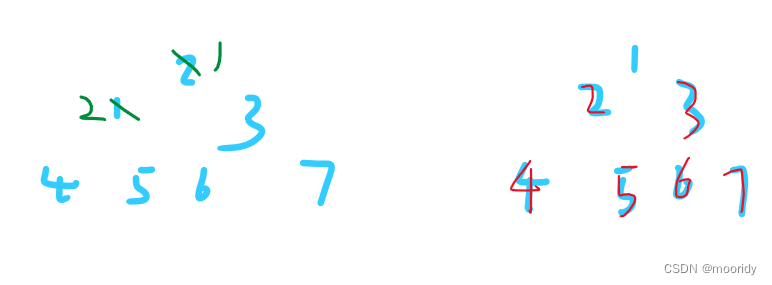
while (n - 1) {swap(&a[0], &a[n - 1]);AdjustDown(a, n-1,0);n--;🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <assert.h>void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0) {if (a[parent] < a[child]) {swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n ) {if (child + 1 < n && a[child] < a[child + 1]) {child++;}if (a[parent] < a[child]) {swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else {break;}}
}//升序建大堆 降序建小堆
void HeapSort(int* a, int n) {//建堆:从倒数第一个父节点开始向前遍历,向下调整for (int i = (n-1-1)/2; i >=0 ;i--) {AdjustDown(a,n,i);}//先将首尾元素进行交换,再向下调整while (n - 1) {swap(&a[0], &a[n - 1]);AdjustDown(a, n-1,0);n--;}
}int main() {int a[7] = { 2,6,5,1,7,4,3 };int n = sizeof(a) / sizeof(a[0]);HeapSort(a, n);for (int i = 0; i < n; i++) {printf("%d ",a[i]);}return 0;
}🍉从时间复杂度角度分析建堆为何采取向下调整?
下面将分别分析向下调整算法建堆和向上调整算法建堆的区别:
向下调整建堆
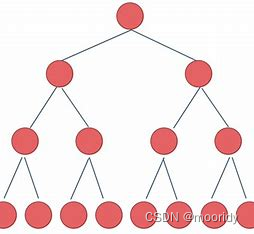
假设节点数量为N,树的高度为h
第一层,2^0个节点,需要向下调整h-1层
第二层,2^1个节点,需要向下调整h-2层
第三层,2^2个节点,需要向下调整h-3层
……
第h层,2^h个节点,需要向下调整0层
可以看出:节点少的层向下调整得多,节点多的层向下调整得少
计算向下调整建堆最坏情况下合计的调整次数:
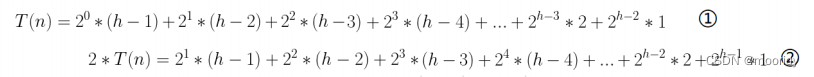
通过错位相减法可得:
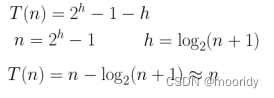
因此向下调整建堆的时间复杂度为O(N)
向上调整建堆:

假设节点数量为N,树的高度为h
第一层,2^0个节点,需要向下调整0层
第二层,2^1个节点,需要向下调整1层
第三层,2^2个节点,需要向下调整2层
……
第h层,2^h个节点,需要向下调整h-1层
可以看出:节点少的层向上调整得少,节点多的层向上调整得多。
T(h)=2^1*1+2^2*2+……+2^(h-2)*(h-2)+2^(h-1)*(h-1)
同样由错位相减法可得:
T(h)=-(2^2+2^3+……+2^(h-1))+2^h*(h-1)-2^1
整理可得:
T(N)=-N+(N+1)*(log2(N+1)-1)+1
因此向上调整建堆的时间复杂度为O(N*logN)
所以我们选择向下建堆算法明显效率更高。
相关文章:

数据结构 | 详解二叉树——堆与堆排序
🥝堆 堆总是一棵完全二叉树。 大堆:父节点总是大于子节点。 小堆:父节点总是小于子节点。 注意:1.同一个节点下的两个子节点并无要求先后顺序。 2.堆可以是无序的。 🍉堆的实现 🌴深度剖析 1.父节点和子…...

vb.net,C#强制结束进程,“优雅”的退出方式
在VB.NET中,Application.Exit()和Environment.Exit(0)都用于结束程序,但它们的使用场景和背后的逻辑略有不同。 **Application.Exit()**: Application.Exit()通常用于Windows Forms应用程序中。当调用Application.Exit()时,它会触…...

牛客热题:数据流中的中位数
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:数据流中的中位数题目链接方法一…...
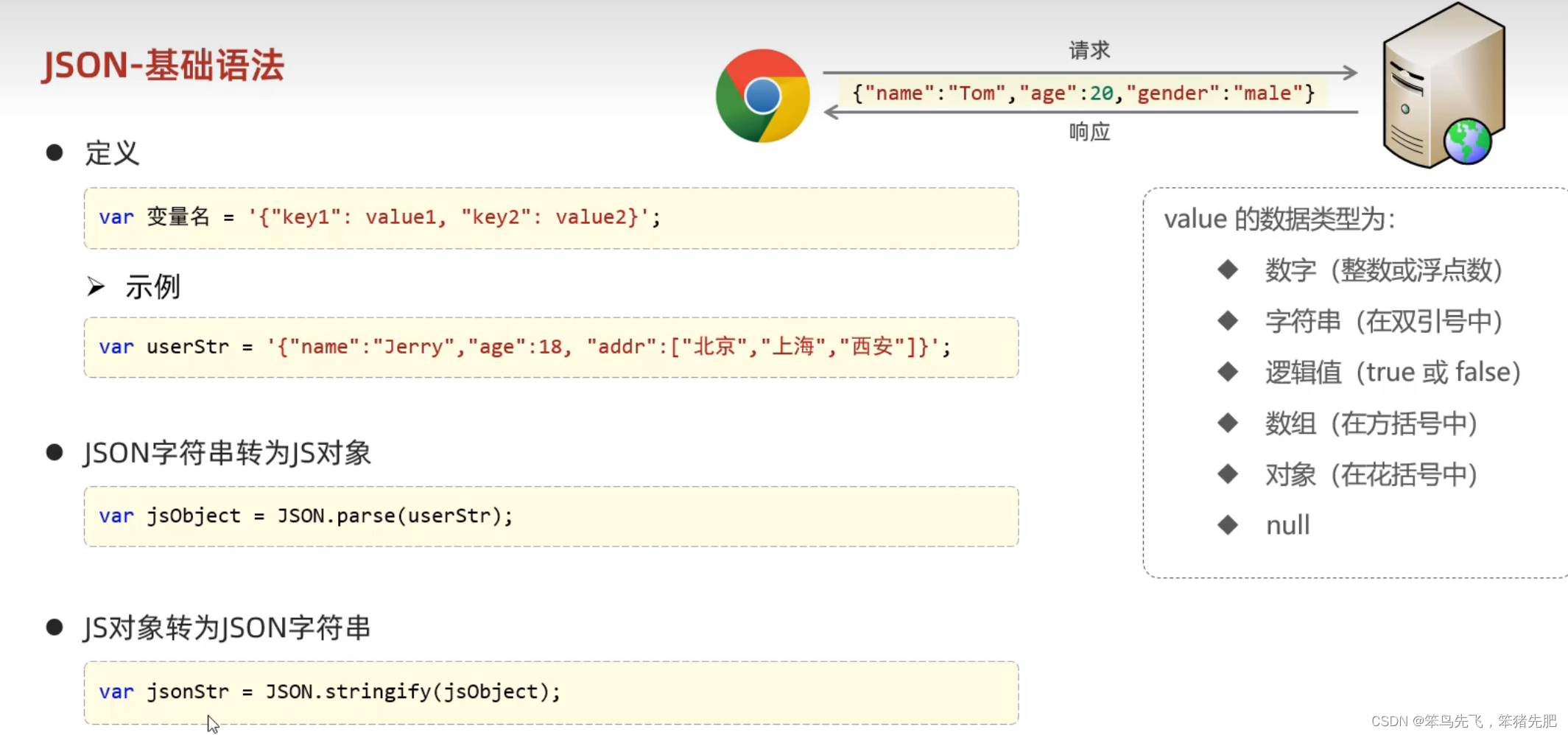
JavaScript-JavaWeb
目录 什么是JavaScript? js引入方式 js基础语法 书写语法 变量 数据据类型 运算符 类型转换 流程语句 js函数 js对象 1.Array 2.String 3.JSON js事件监听 什么是JavaScript? ● JavaScript(简称:JS)是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能…...

vue组件通讯$parent和$children获取单签组件的⽗组件和当前组件的⼦组件的例子
在 Vue 中,$parent 和 $children 是实例属性,允许你访问组件的父组件和子组件。但是,请注意,这些属性主要用于在开发过程中进行调试和临时访问,并不推荐在正常的组件通信中使用,因为它们破坏了组件的封装性…...

Util和utils
Util FieldStats 这段代码定义了一个名为FieldStats的Java类,位于com.cqupt.software_1.Util包中。它使用了lombok库的Data和AllArgsConstructor注解,这些注解帮助生成了getter、setter、toString等方法,以及包含所有参数的构造函数。类中有…...
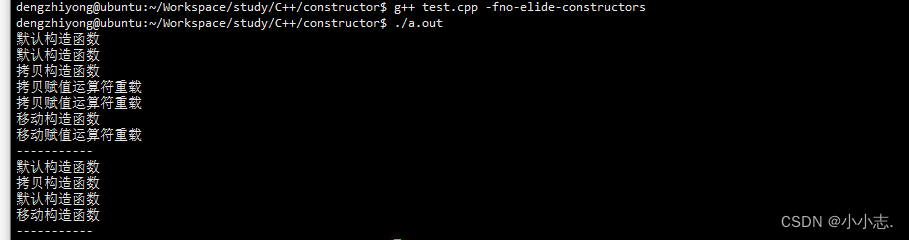
拷贝构造、移动构造、拷贝赋值、移动赋值
最近在学习C的拷贝构造函数时发现一个问题:在函数中返回局部的类对象时,并没有调用拷贝构造函数。针对这个问题,查阅了一些资料,这里记录整理一下。 调用拷贝构造函数的三种情况: ① 用一个类去初始化另一个对象时&a…...

Python3 笔记:math模块
要使用 math 函数必须先导入math模块 语法:import math Python math 模块提供了许多对浮点数的数学运算函数。 math 模块下的函数,返回值均为浮点数,除非另有明确说明。 如果需要计算复数,需使用 cmath 模块中的同名函数。 m…...

python -【四】函数
函数 一、函数的基础 函数:是组织好的,可以重复使用的,用来实现特定功能的代码段 语法 def 函数名(入参): return 出参 # 定义函数 def out_hello():print(hello ~~~)# 调用/使用/执行函数 out_hello()练习题 自定义一个函数,…...

力扣 5. 最长回文子串 python AC
动态规划 class Solution:def longestPalindrome(self, s):size len(s)maxl 1start 0dp [[False] * size for _ in range(size)]for i in range(size):dp[i][i] Truefor L in range(2, size 1):for i in range(size):j L i - 1if j > size:breakif s[i] s[j]:if L…...
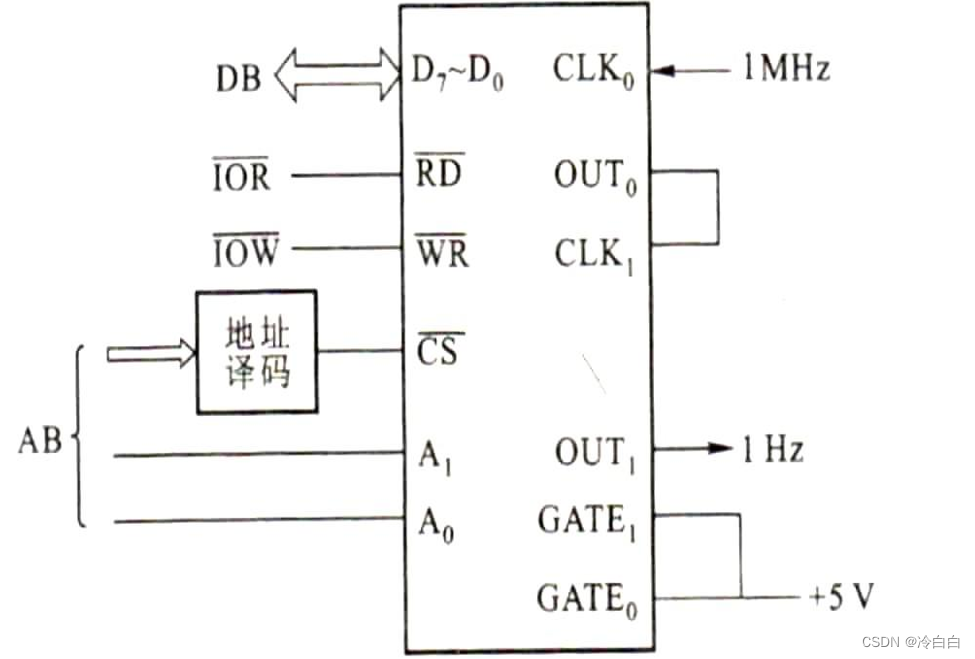
【微机原理及接口技术】可编程计数器/定时器8253
【微机原理及接口技术】可编程计数器/定时器8253 文章目录 【微机原理及接口技术】可编程计数器/定时器8253前言一、8253的内部结构和引脚二、8253的工作方式三、8253的编程总结 前言 本篇文章就8253芯片展开,详细介绍8253的内部结构和引脚,8253的工作方…...

23种设计模式之一— — — —装饰模式详细介绍与讲解
装饰模式详细讲解 一、定义二、装饰模式结构核心思想模式角色模式的UML类图应用场景模式优点模式缺点 实例演示图示代码演示运行结果 一、定义 装饰模式(别名:包装器) 装饰模式(Decorator Pattern)是结构型的设计模式…...

2024年2月28日 星期三
2024年2月28日 星期三 农历正月十九 1. 住建部:各城市要做好今明两年住房发展计划,防止市场大起大落。 2. 政协委员赵长龙建议:增加元旦、端午、中秋高速免费,周六日半价。 3. 人民法院案例库开始对社会开放,与中国…...

Java中的super关键字详解
在Java编程中,super关键字是一个非常重要的概念,尤其是在继承和多态的场景中。理解super关键字的使用方法和其背后的机制,对于掌握面向对象编程(OOP)的基本概念至关重要。本篇博客将详细讲解super关键字的各种用法及其…...

消消乐游戏开发,三消游戏,消除小游戏
消消乐是一款非常受欢迎的休闲消除类游戏,通常也被称为“三消游戏”。这类游戏的主要目标是通过交换和匹配三个或更多相同的物品来清除它们,从而得分并通过关卡。以下是一些消消乐游戏的基本特点和玩法: 基本玩法 交换和匹配:玩…...
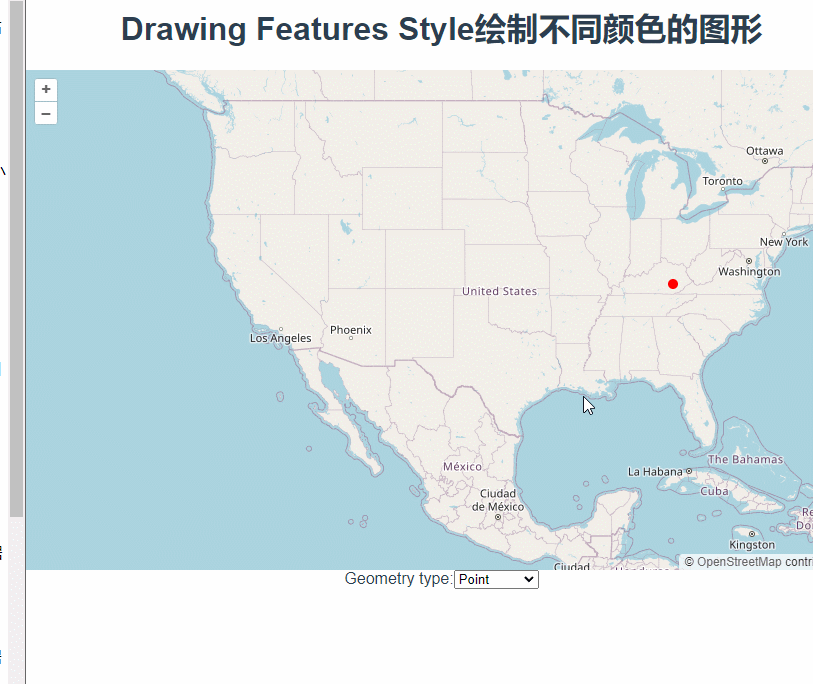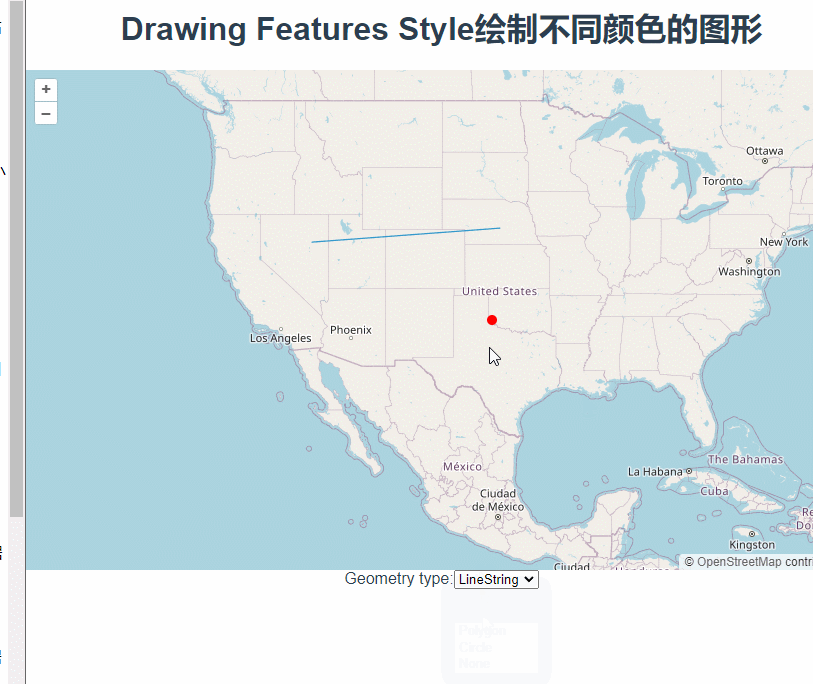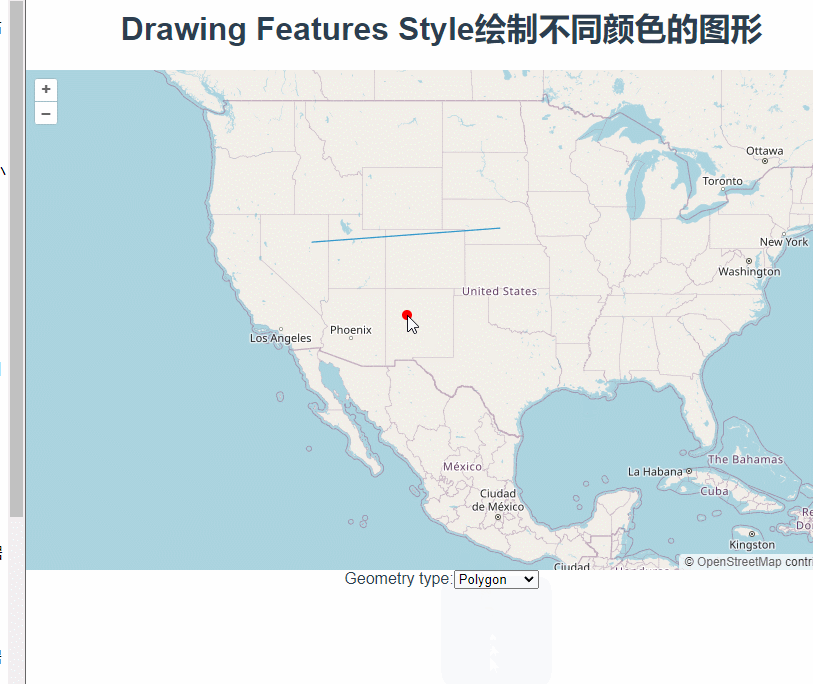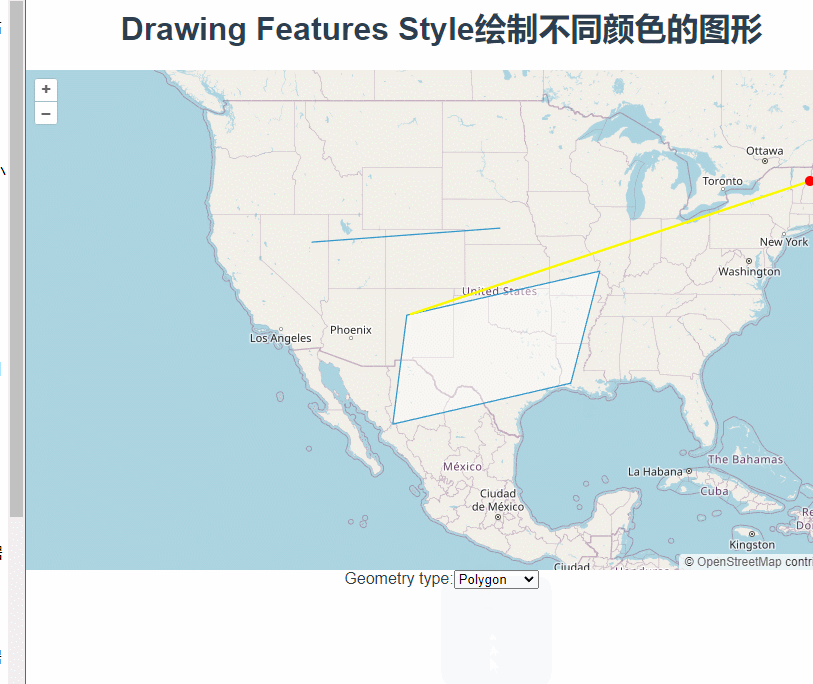
三十三、openlayers官网示例Drawing Features Style——在地图上绘制图形,并修改绘制过程中的颜色
这篇讲的是使用Draw绘制图形时根据绘制形状设置不同颜色。 根据下拉框中的值在styles对象中取对应的颜色对象,new Draw的时候将其设置为style参数。 const styles {Point: {"circle-radius": 5,"circle-fill-color": "red",},LineS…...
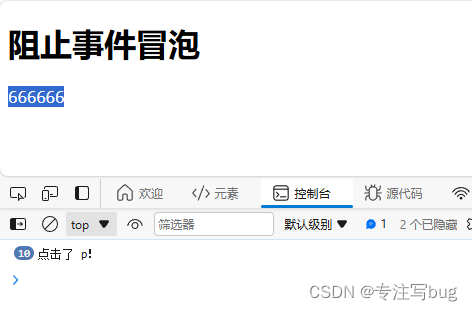
Vue——事件修饰符
文章目录 前言阻止默认事件 prevent阻止事件冒泡 stop 前言 在官方文档中对于事件修饰符有一个很好的说明,本篇文章主要记录验证测试的案例。 官方文档 事件修饰符 阻止默认事件 prevent 在js原生的语言中,可以根据标签本身的事件对象进行阻止默认事件…...
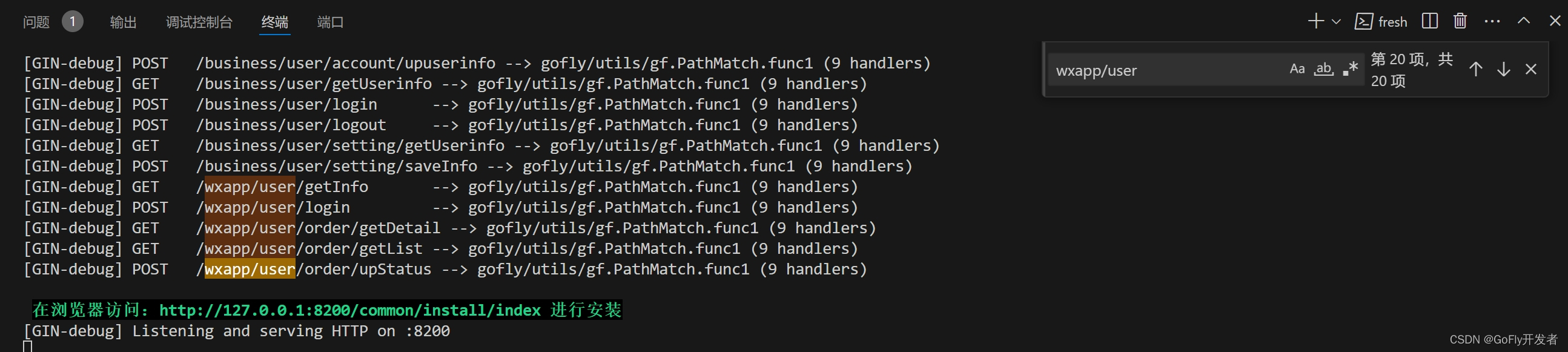
Go语言GoFly框架快速新增接口/上手写代码
拿到一个新框架大家可能无从下手,因为你对框架设计思路、结构不了解,从而产生恐惧,所以我们框架是通过简单可视化界面安装,安装后即可看到效果,然后点击先点点看各个功能,看现有的功能是怎么写的࿰…...

【Vue】v-else 和 v-else-if
作用:辅助v-if进行判断渲染 语法: v-else v-else-if"表达式"PS:需要紧接着v-if使用 示例代码: <body><div id"app"><p v-if"gender 1">性别:♂ 男</p><…...
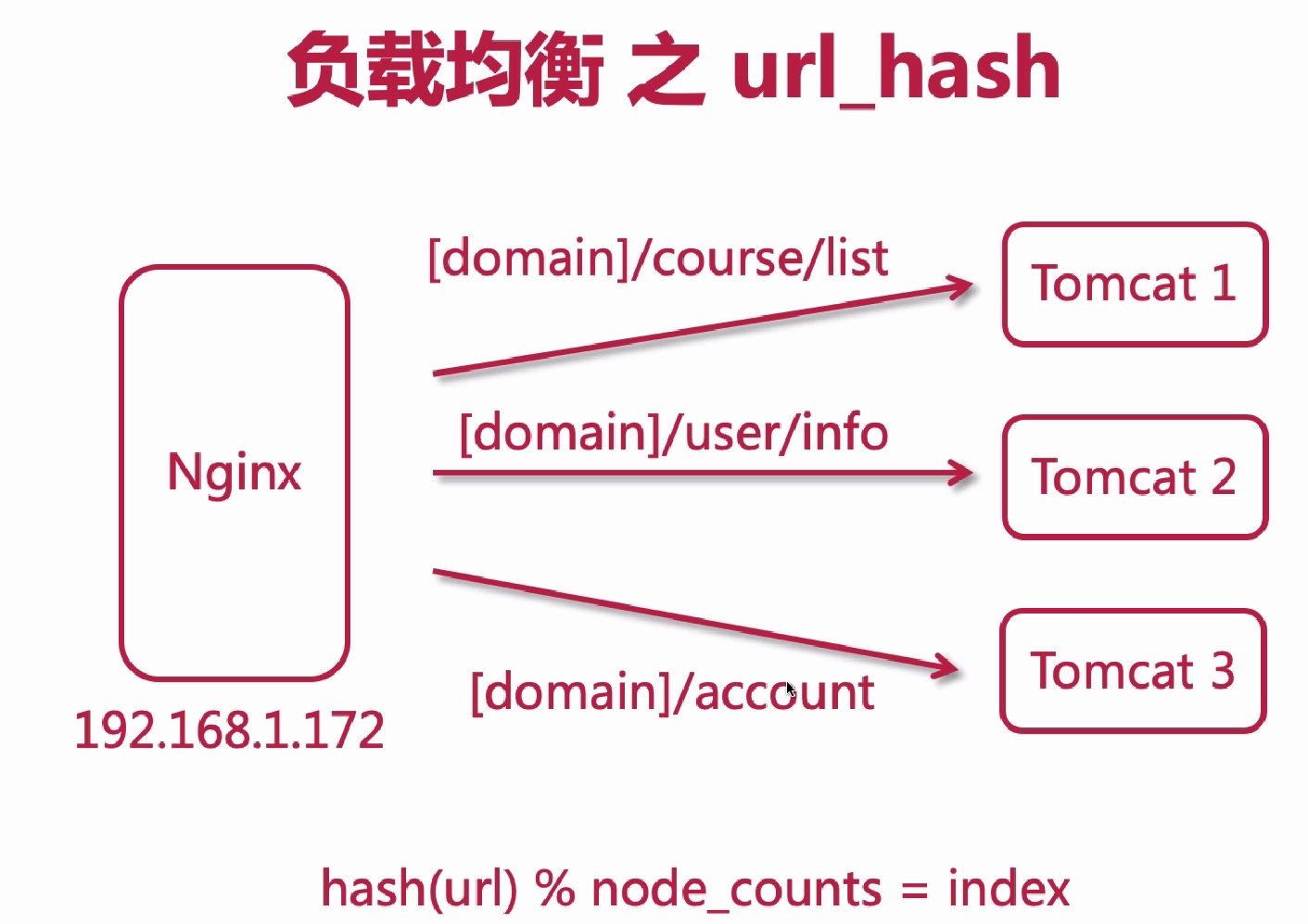
一致性hash算法原理图和负载均衡原理-urlhash与least_conn案例
一. 一致性hash算法原理图 4台服务器计算hash值图解 减少一台服务3台服务器计算hash值图解 增加一台服务器5台服务器计算hash值图解 二. 负载均衡原理-urlhash与least_conn 2.1.urlhash案例 # urlhash upstream tomcats {hash $requ...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

