条件竞争漏洞
条件竞争漏洞
postMessage的客户端竞争条件
Summary
- AppCache可以被利用来强制浏览器加载后备的HTML页面,允许像Cookie填充(stuffing)这样的攻击,迫使出错并泄露敏感的URL。在负责任披露后,这个问题已经在各大浏览器中得到修复。
- 对AWS S3和Google Cloud等云存储的上传策略(upload policy)实现不当,可能允许攻击者覆盖任何文件或访问根目录。自定义的正则表达式策略也容易被绕过。
- frame之间通过postMessage进行的通信可能导致沙箱域的XSS漏洞、通过复杂规则集提取数据以及客户端竞争条件(如果消息未被正确验证和处理)等漏洞。像postMessage-tracker这样的工具可以帮助审计这些消息流。
- 常见的JS框架如jQuery、Raven、Rollbar等会阻碍对postMessage监听器的分析,需要使用一些变通方法。
Step
- AppCache技术复现需要准备恶意的manifest文件,并让受害者访问设置了该文件路径的页面,以便强制浏览器加载后备HTML页面。
- 针对上传策略漏洞的复现,需要通过接口获取带有漏洞的策略签名,然后构造恶意上传请求绕过限制。
- postMessage通信的测试需要开发浏览器扩展或利用多frame页面,在不同域之间发送消息,并分析返回结果判断是否存在问题。
- 框架对postMessage监听的影响可以通过在同一页面引入该框架与postMessage通信的代码进行复现。
Impact
- AppCache漏洞能够绕过同源策略,可能导致敏感信息泄露、页面劫持等后果。
- 上传策略绕过使攻击者能够未授权访问或修改后端存储中的文件,危害数据安全。
- postMessage通信过程中的验证缺陷可能被利用进行XSS攻击、CSRF攻击、信息窃取等。
- 框架对postMessage监听的影响会减弱安全测试的效果,导致潜在问题被忽略。
扩展
Paper
postMessage的客户端竞争条件
postMessage的客户端竞争条件
相关文章:

条件竞争漏洞
条件竞争漏洞 postMessage的客户端竞争条件 Summary AppCache可以被利用来强制浏览器加载后备的HTML页面,允许像Cookie填充(stuffing)这样的攻击,迫使出错并泄露敏感的URL。在负责任披露后,这个问题已经在各大浏览器中得到修复。对AWS S3和Google Cloud等云存储的上传策略(u…...

磁带存储:“不老的传说”依然在继续
现在是一个数据指数增长的时代,根据IDC数据预测,2025年全世界将产生175ZB的数据。 这里面大部分数据是不需要存储的,在2025预计每年需要存储11ZB的数据。换算个容易理解的说法,1ZB是10^18Bytes, 相当于要写5556万块容量18TB的硬盘…...

CentOS8环境下FTP服务器安装与配置
在本指南中,我们将一步步介绍如何在CentOS 8环境下安装和配置一个FTP服务器。FTP(文件传输协议)是一种网络传输协议,用于在网络中的计算机之间传输文件。虽然现在有更安全的传输方式,如SFTP或FTP over SSL,…...

C# 元组 Tuple
C# 元组 Tuple 元组创建元组访问元组元素命名元组元素元组的类型使用元组作为方法返回值 解构解构元组的基本用法解构部分元组解构方法 元组 在C#中,元组(Tuple)是一种数据结构,它允许你将多个值组合成一个单一的对象。 元组在处…...

100个投资者99个选择使用这款EA,WeTrade发现1个事实
为什么100个投资者会有99个选择使用这款EA,是因为这款EA能提供两个版本吗?是因为能控制风险吗?都不是,WeTrade发现1个事实才是这么多投资者选择的原因,那就是能实现100%的盈利率。 我们都知道外汇狙击手EA提供两种版本,分别是标…...

爬虫面试手册
爬虫面试手册 薪资13~20k 岗位职责: 负责公司数据平台的数据采集、运维优化;负责自动化脚本,爬虫脚本;研究数据采集策略和防屏蔽规则,提升数据采集系统的稳定性、可扩展性,提高抓取的效率和质量; 岗位要求 本科及…...
)
k8s cephfs(动态pvc)
官方参考文档:GitHub - ceph/ceph-csi at v3.9.0 测试版本 Ceph Version Ceph CSI Version Container Orchestrator Name Version Tested v17.2.7 v3.9.0 Kubernetes v1.25.6 安装Ceph-csi Step 1 Download GitHub - ceph/ceph-csi at v3.9.0 rootsd-k8s…...

dubbo复习:(9)配置中心的大坑,并不能像spring cloud那样直接从配置中心读取自定义的配置
配置中心只是为 Dubbo 配置提供管理使用的(比如配置服务超时时间等)。不要尝试通过Value类似的方式从dubbo 配置中心(比如nacos、zookeeper、Apollo)来获取数据 https://github.com/apache/dubbo/issues/11200可以在application.yml中主要写注册中心的配置…...
建设现代智能工业-智能化、数字化、自动化节能减排
建设现代智能工业-智能化节能减排 遵循“一体化”能源管理(Integrated Energy Management)的设计宗旨,集成城市各领域(如工业.交通、建筑等)的能源生产和消费信息,面向城市政府、企业、公众三类实体,提供“一体化”的综合能源管理…...

据报导,SK海力士的HBM团队源自三星,暗示三星不幸失去HBM优势
最新科技动态显示,三星的高带宽记忆体(High Bandwidth Memory, HBM)技术尚未获得GPU巨头英伟达(NVIDIA)的认证,导致其落后于竞争对手SK海力士。这一挫折直接导致三星半导体部门负责人更迭。尽管三星官方否认…...

Verilog HDL基础知识(一)
引言:本文我们介绍Verilog HDL的基础知识,重点对Verilog HDL的基本语法及其应用要点进行介绍。 1. Verilog HDL概述 什么是Verilog?Verilog是IEEE标准的硬件描述语言,一种基于文本的语言,用于描述最终将在硬件中实现…...

Django之文件上传(一)
一、环境搭建 建立项目 django-admin startproject project_demo配置数据库(以MySQL为例) # settings.py DATABASES = {default: {ENGINE: django.db.backends.mysql,NAME: django_file4,USER: root,PASSWORD: 123,HOST: 192.168.31.151,PORT: 3306,} }建立模型 class UploadF…...

光纤现网与接入网概念对应
OLT 一般在机房 一级分光可能在机房也可能在光交交接箱 路边的光交交接箱功能有分光或者光纤汇聚转换一下 二级分光在分光光纤箱里,楼道里面挂着的那种 ONU是家里的光猫...

通过扩展指令增强基于覆盖引导的模糊测试
本文由Bruno Oliveira于2024年4月25日发表于IncludeSec的官方网站上。作为IncludeSec的安全研究人员,在他们日常的安全审计和渗透测试工作中,有时需要为客户开发一些模糊测试工具。在安全评估方法中使用模糊测试技术,可以有效地在复杂的现代化…...
第一节:Redis的数据类型和基本操作
最近整理了关于Redis的一些文档,分享给大家,后续会持续更新...... Redis的数据类型 字符串String String:字符串,可以存储String、Integer、Float型的数据,甚至是二进制数据,一个字符串最大容量是512M 列表…...
组件的传参等
一:组件的生命周期函数 组件的生命周期函数: created只是创建了组件内的实例对象 attached,给组件实例绑定了属性,绑定到页面节点树之后 ready准备好渲染之后,还未渲染之前 moved组件实例被移动到另一个位置后执行 detached在整个组件被被移除执行 error执行的时候,组件内…...
构建php环境、安装、依赖、nginx配置、ab压力测试命令、添加php-fpm为系统服务
目录 php简介 官网php安装包 选择下载稳定版本 (建议使用此版本,文章以此版本为例) 安装php解析环境 准备工作 安装依赖 zlib-devel 和 libxml2-devel包。 安装扩展工具库 安装 libmcrypt 安装 mhash 安装mcrypt 安装php 选项含…...
服装服饰商城小程序的作用是什么
要说服装商家,那数量是非常多,厂家/经销门店/小摊/无货源等,线上线下同行竞争激烈,虽然用户群体广涵盖每个人,但每个商家肯定都希望更多客户被自己转化,渠道运营方案营销环境等不可少。 以年轻人为主的消费…...
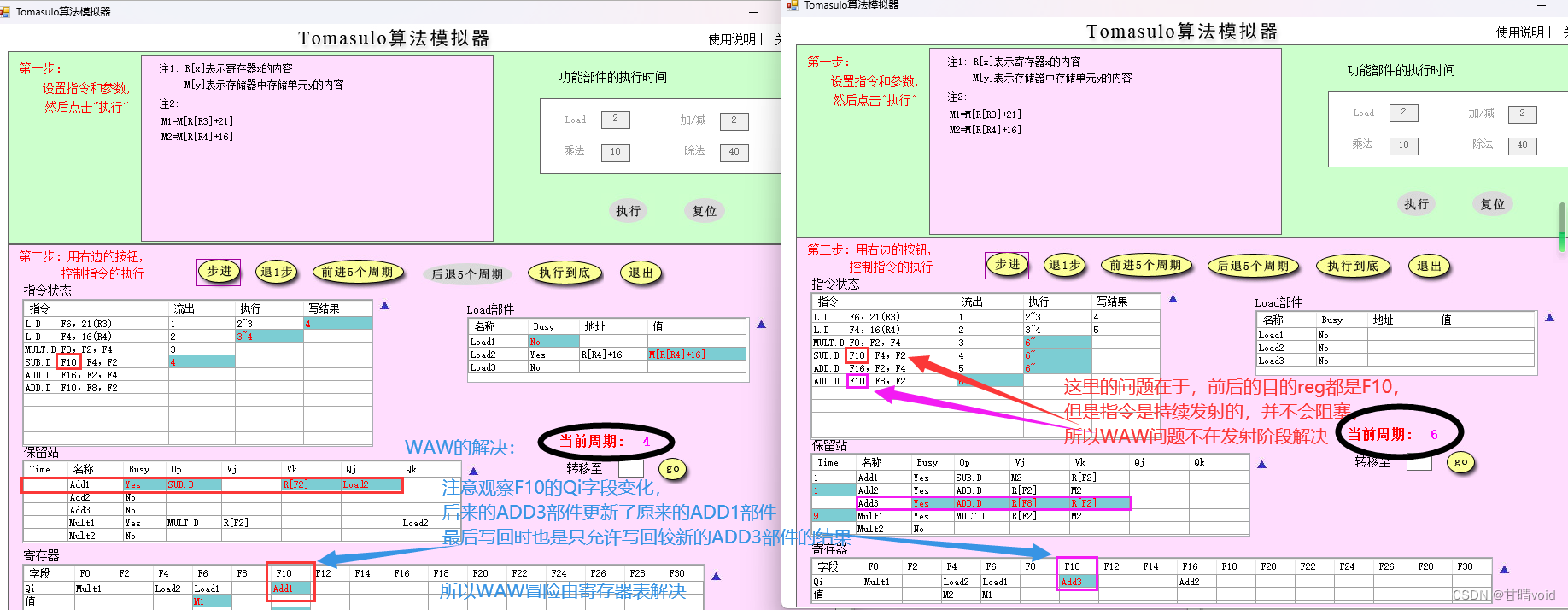
HNU-计算机体系结构-实验2-Tomasulo算法
计算机体系结构 实验2 计科210X 甘晴void 202108010XXX 1 实验目的 熟悉Tomasulo模拟器同时加深对Tomasulo算法的理解,从而理解指令级并行的一种方式-动态指令调度。 掌握Tomasulo算法在指令流出、执行、写结果各阶段对浮点操作指令以及load和store指令进行什么…...

深入分析 Android Activity (一)
文章目录 深入分析 Android Activity (一)1. Activity 的窗口管理2. Activity 的生命周期管理onCreateonStartonResumeonPauseonStoponDestroyonRestart 3. Activity 与 Fragment 的交互添加 FragmentFragment 的生命周期 4. Activity 的任务和返回栈5. 配置变化处理 总结 深入…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
