基于GO 写的一款 GUI 工具,M3u8视频下载播放器-飞鸟视频助手
M3u8视频下载播放器-飞鸟视频助手
- M3u8视频
- 飞鸟视频助手使用
- m3u8下载
- m3u8 本地播放
- 软件下载地址
- m3u8嗅探
M3u8视频
M3u8视频格式是为网络视频播放设计,视频网站多数采用 m3u8格式。如腾讯,爱奇艺等网站。
m3u8和 mp4的区别:
一个 mp4是一个独立的文件。
m3u8是一组文件,多至几百几千个。
mp4视频分辨率是固定的。
m3u8视频可以包含不同分辨率的多个视频。

飞鸟视频助手使用
飞鸟视频助手是一个方便用户下载播放m3u8视频的工具。 有 GUI 界面,可跨平台使用。
m3u8下载
复制输入m3u8地址, 点击开始下载。
在下载前可点击“播放检查” 确认m3u8地址正确。

m3u8 本地播放

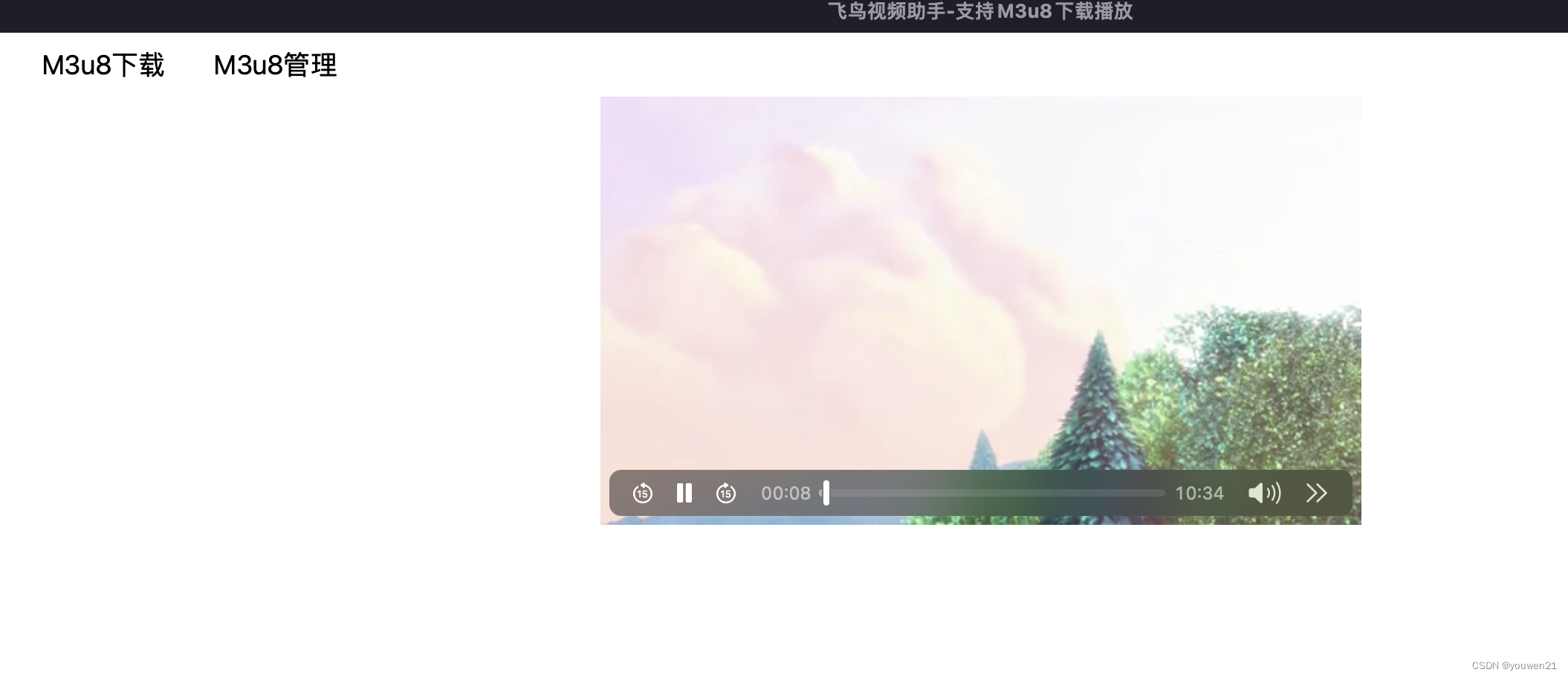
软件下载地址
https://github.com/youwen21/flybird-m3u8downloader/releases
m3u8嗅探
关于 M3u8 的嗅探,个人推荐 “猫抓” 插件。 可在 github或者chrome 插件市场找到。
相关文章:

基于GO 写的一款 GUI 工具,M3u8视频下载播放器-飞鸟视频助手
M3u8视频下载播放器-飞鸟视频助手 M3u8视频飞鸟视频助手使用m3u8下载m3u8 本地播放 软件下载地址m3u8嗅探 M3u8视频 M3u8视频格式是为网络视频播放设计,视频网站多数采用 m3u8格式。如腾讯,爱奇艺等网站。 m3u8和 mp4的区别: 一个 mp4是一个…...

关于EasyExcel导入数据时表格日期格式识别为数字问题
参考官方地址 自定义日期转字符串转换器 /*** 自定义excel日期转换器** author li* date 2024-05-29*/ public class CustomStringDateConverter implements Converter<String> {Overridepublic Class<?> supportJavaTypeKey() {return String.class;}Overridep…...

高通Android 12/13打开省电模式宏开关
1、添加到SettingsProvider配置项宏开关 默认节电助手自动开启百分比battery saver frameworks\base\packages\SettingsProvider\src\com\android\providers\settings\DatabaseHelper.java private void loadGlobalSettings(SQLiteDatabase db) {在该方法中添加 ......final i…...

2023年西安交通大学校赛(E-雪中楼)
E.雪中楼 如果算出按南北的序列,再转成从低到高的编号序列,岂不是太麻烦了,幸好,没有在这方面费长时间,而是意识到,本质就是要从低到高的编号序列,所以我就按样例模拟了一下,当a[i]0…...

如何在vue2中使用tailwind
查看官方文档,不要去看过时的文章! 使用官网推荐的第一个安装方法 Installation - Tailwind CSS vue版本:2.6.10 1. 安装tailwind的包 npm install -D tailwindcss npx tailwindcss init 2. tailwind.config.js 文件中的content是你需要…...

【OrangePi AIpro】开箱初体验以及OAK深度相机测试
1. 简介 Orangepi AIPRO 是一款采用昇腾AI技术路线,集成4核64位处理器AI处理器的单板计算机,集成图形处理器,支持8TOPS AI算力,拥有8GB/16GB LPDDR4X,可以外接eMMC模块,支持双4K高清输出。 Orange Pi AIpr…...
)
滑动窗口模板(Java)
题目描述 有一个长为 𝑛 的序列 𝑎,以及一个大小为 𝑘 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。 例如,对于序列 [1,3,−1,−3,5,3,6,7] …...

transformers.BertTokenizer入门使用
教程link 示例代码 from transformers import OpenAIGPTLMHeadModel, GPT2LMHeadModel, BertTokenizer import torch tokenizer BertTokenizer.from_pretrained("thu-coai/CDial-GPT_LCCC-large") model OpenAIGPTLMHeadModel.from_pretrained("thu-coai/CD…...

快乐数-力扣
使用一个set来存储遇到的每个数,如果遇到的数在set中,那么说明这个数不是快乐数,否则一直循环下去,直到n 1结束循环,表示这个数是个快乐数。 需要注意的是,给定一个数 n, 怎样对这个数 n 进行每一位求和。…...

Git标签的使用
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
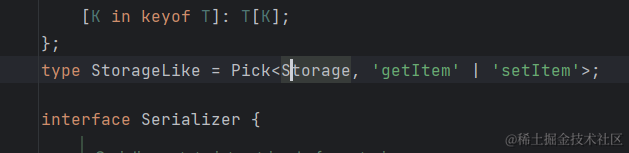
【uni-app】Pinia 持久化
小程序端 Pinia 持久化 说明:Pinia 用法与 Vue3 项目完全一致,uni-app 项目仅需解决持久化插件兼容性问题。 持久化存储插件 安装持久化存储插件: pinia-plugin-persistedstate pnpm i pinia-plugin-persistedstate插件默认使用 localStor…...

Flink 窗口
窗口(Window) 窗口是处理无限流的核心。 窗口将流分割成有限大小的“桶”,我们可以计算窗口中的数据。 窗口程序一般有键控流(keyed streams)的窗口程序 和 非键控流(non-keyed streams)的窗口…...

基于大模型和RAG技术实现的开源项目
基于大模型和RAG技术实现的开源项目 为解决大模型的不足,使用RAG技术增强大模型生成内容的针对性和可读性能力,有很多不错的开源项目。例如下面的项目。 1 ragflow 优点:可以对文档和知识库进行管理,构建不同的知识库ÿ…...
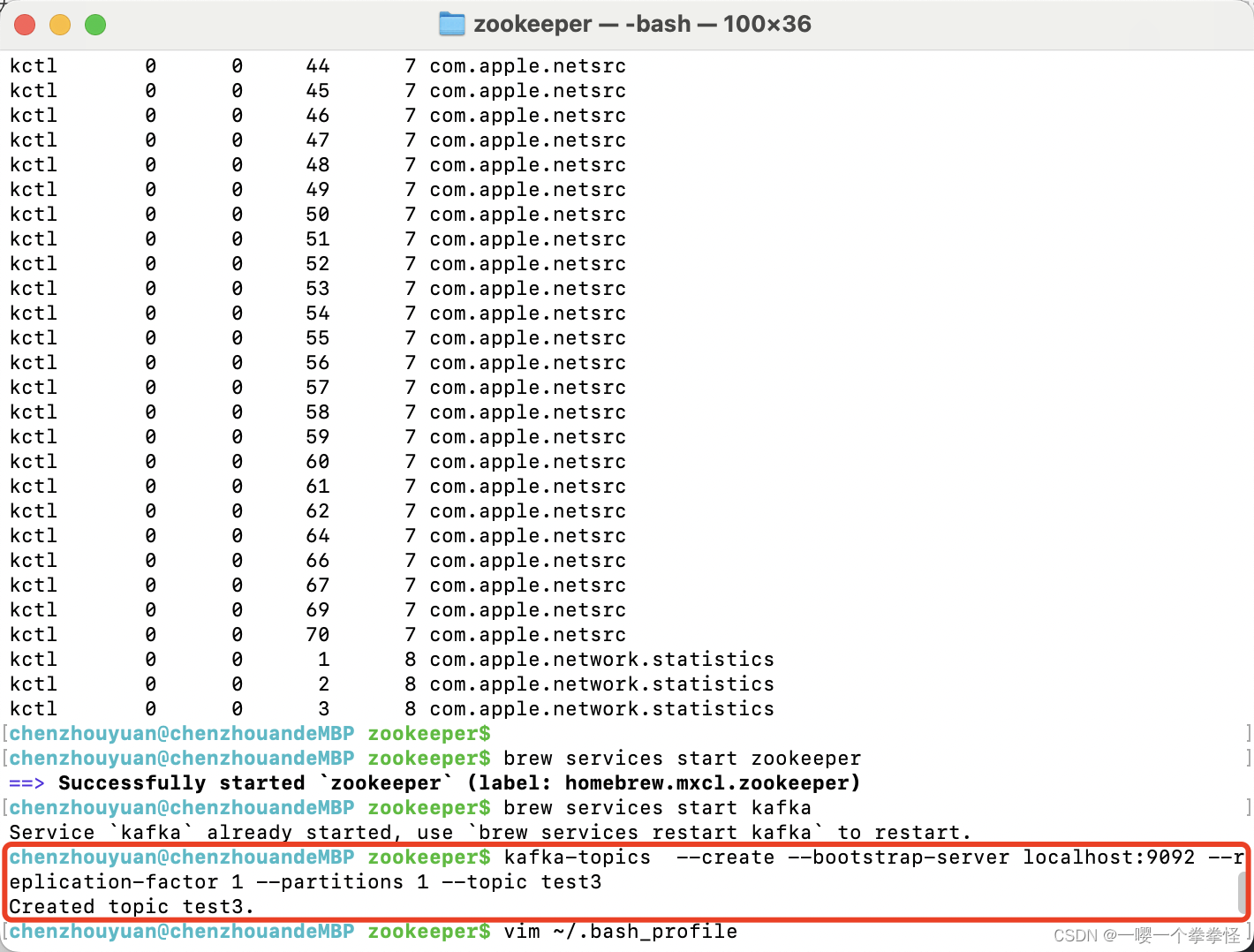
mac m1安装homebrew管理工具(brew命令)完整流程
背景 因为mac上的brew很久没用了,版本非常旧,随着mac os的更新,本机的homebrew大部分的功能都无法使用,幸好过去通过brew安装的工具比较少,于是决定重新安装一遍brew。 卸载旧版brew 法一:通过使用线上…...

Liunx学习随笔
Linux学习随笔 Linux学习随笔一.前期准备1.安装Vmware Workstation软件2.下载linux镜像3.安装操作系统4.配置静态ip5.下载安装远程连接工具 二.语法2.1 linux哲学思想(原则)2.2 小命令 夕阳无限好,只是近黄昏,时隔一年,重新提笔 没有比脚更远…...

mac中文件夹怎么显示.git隐藏文件
1. 打开终端应用程序,然后进入到包含.git文件夹的目录,可以使用以下命令来显示隐藏文件和文件夹: defaults write com.apple.finder AppleShowAllFiles YES 2. 然后重启 Finder: killall Finder...
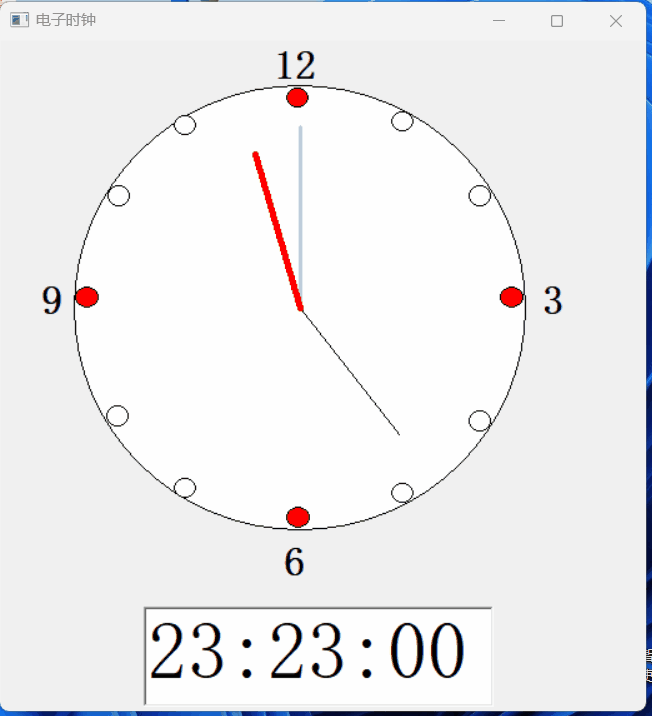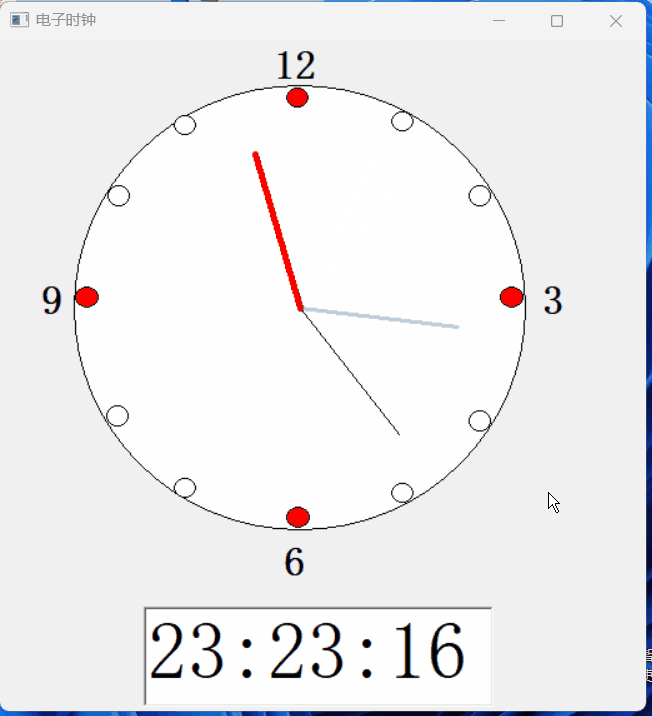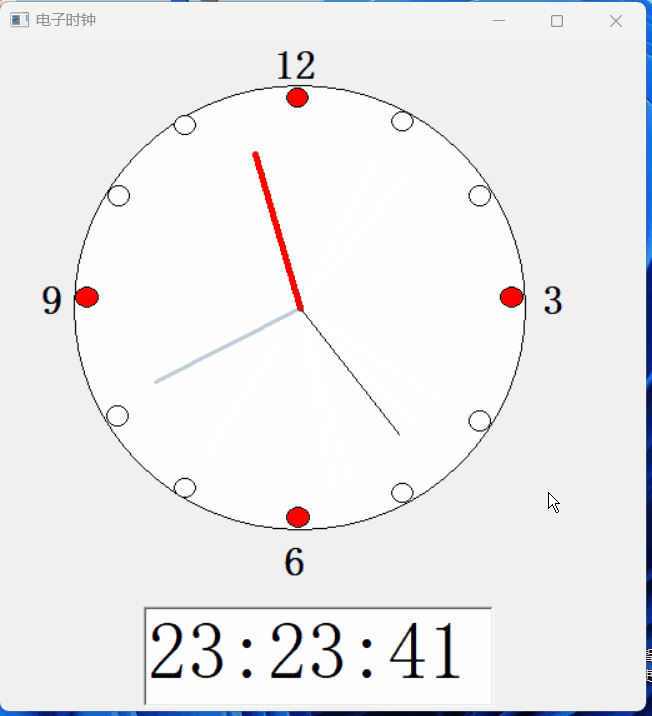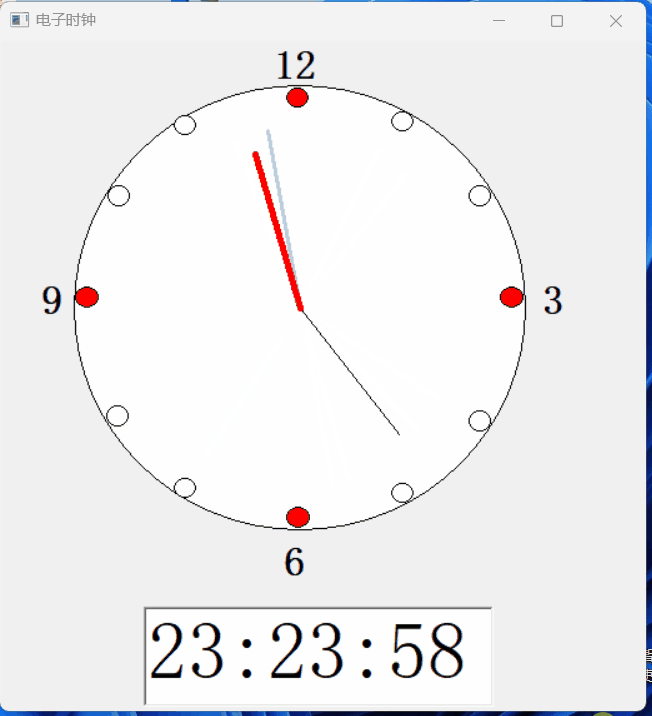
【PB案例学习笔记】-13 徒手做个电子时钟
写在前面 这是PB案例学习笔记系列文章的第11篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gite…...

Java多线程——线程强制执行
Join合并线程,待此线程执行完成后,再执行其他线程,其他线程阻塞。 可以想象成插队。 代码演示: //测试Join方法 //想象为插队 public class TestJoin implements Runnable{Overridepublic void run() {for (int i 0; i < 1…...

虹科Pico汽车示波器 | 免拆诊断案例 | 2017款奔驰E300L车行驶中发动机偶尔无法加速
故障现象 一辆2017款奔驰E300L车,搭载274 920发动机,累计行驶里程约为21万km。车主反映,该车行驶中发动机偶尔无法加速,且车辆发闯。 故障诊断 用故障检测仪检测,发动机控制单元(N3/10)中存储…...

华发股份:加强业务协同 新政下项目热销
“5.17”楼市政策出台后,各地密集落地执行。5月27—28日,上海、广州、深圳三个一线城市跟进落地“517”新政。上海发布《关于优化本市房地产市场平稳健康发展政策措施的通知》,共计9条调整政策,涵盖外地户籍、人才、单身、婚否、企…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...

Linux系统:进程间通信-匿名与命名管道
本节重点 匿名管道的概念与原理匿名管道的创建命名管道的概念与原理命名管道的创建两者的差异与联系命名管道实现EchoServer 一、管道 管道(Pipe)是一种进程间通信(IPC, Inter-Process Communication)机制,用于在不…...

7种分类数据编码技术详解:从原理到实战
在数据分析和机器学习领域,分类数据(Categorical Data)的处理是一个基础但至关重要的环节。分类数据指的是由有限数量的离散值组成的数据类型,如性别(男/女)、颜色(红/绿/蓝)或产品类…...
