使用python求PLS-DA的方差贡献率
以鸢尾花数据集为例,实现PLS-DA降维,画出降维后数据的散点图并求其方差贡献率。
效果图
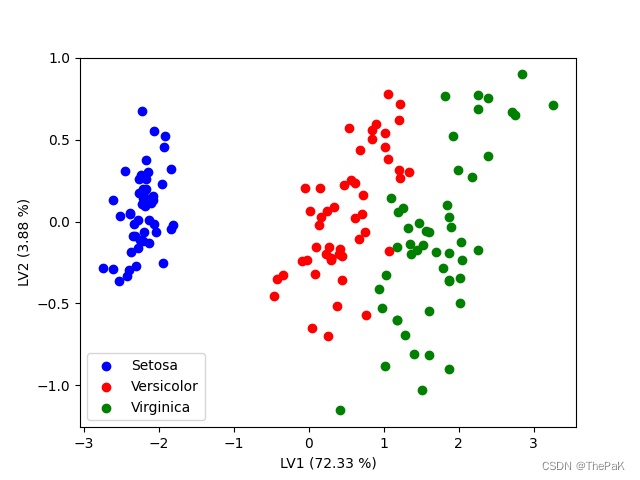
完整代码
# 导入所需库
import numpy as np
from sklearn.cross_decomposition import PLSRegression
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt# 载入数据
iris = load_iris()
X = iris.data
y = iris.target
print(X.shape)
print(y.shape)
# 标准化数据
X = StandardScaler().fit_transform(X)# 定义PLS-DA对象并拟合数据
plsda = PLSRegression(n_components=2)
plsda.fit(X, y)# 得到PLS-DA降维后的数据
X_plsda = plsda.transform(X)
print(X_plsda.shape)
# 绘制散点图
colors = ['blue', 'red', 'green']
labels = ['Setosa', 'Versicolor', 'Virginica']
for i in range(len(colors)):x = X_plsda[:, 0][y == i]y_plot = X_plsda[:, 1][y == i]plt.scatter(x, y_plot, c=colors[i], label=labels[i])# 输出成分贡献率
# 计算PLS-DA成分贡献率# 计算PLSDA的旋转系数
plsda_components = plsda.x_rotations_
print(plsda_components)
plsda_scores = X_plsda
# 计算PLSDA成分解释的方差比例
variance_explained = np.var(plsda_scores, axis=0) # 计算在PLSDA成分上解释的方差
print("variance_explained shape:", variance_explained.shape)
print("variance_explained:", variance_explained)
total_variance = np.var(X, axis=0) # 计算在原始数据上总方差的和
print("total_variance shape:", total_variance.shape)
print("total_variance:", total_variance)
plsda_variance_ratio = variance_explained / total_variance.sum()
print("total_variance.sum():", total_variance.sum()) # 计算PLSDA成分解释的方差比例
# print(plsda_variance_ratio)
# 输出成分贡献率
for i, ratio in enumerate(plsda_variance_ratio):print(f'PLS-DA Component {i + 1}: {ratio * 100:.2f}%')plt.xlabel('LV1 ({} %)'.format(round(plsda_variance_ratio[0] * 100, 2)))
plt.ylabel('LV2 ({} %)'.format(round(plsda_variance_ratio[1] * 100, 2)))plt.legend()
plt.show()代码解析
主要解析求成分贡献率的过程:
plsda_components = plsda.x_rotations_
plsda_scores = X_plsda
variance_explained = np.var(plsda_scores, axis=0)
total_variance = np.var(X, axis=0)
plsda_variance_ratio = variance_explained / total_variance.sum()
plsda.x_rotations_:plsda是进行PLS-DA的对象,plsda.x_rotations_是PLS-DA模型中X变量(即自变量)的旋转矩阵,表示如何将原始数据X映射到新的降维空间中。将该旋转矩阵存储到变量plsda_components中。对于此数据集,得到的plsda_components是4x2的矩阵。
X_plsda:这是使用PLS-DA降维后的X变量数据集,是150×2的矩阵。
variance_explained = np.var(plsda_scores, axis=0):计算每个主成分(即降维后的新变量)在降维后数据中的方差解释比例,存储到变量variance_explained中。这里使用np.var()函数计算方差。由于本次代码是使用PLS-DA将数据降到2维,故得到的variance_explained是一个包含2个元素的一维数组[2.89312513 0.15504989],表示每个特征的方差之和。
total_variance = np.var(X, axis=0):计算原始数据X中每个变量的总方差,存储到变量total_variance中。原始数据是150×4的矩阵,故total_variance是一个包含4个元素的一维数组,[1. 1. 1. 1.]。
plsda_variance_ratio = variance_explained / total_variance.sum():计算每个主成分在总方差中的方差解释比例,即PLS-DA的方差解释比例。将结果存储到变量plsda_variance_ratio中。total_variance.sum()是求总方差的和,即每个变量的方差之和。这里total_variance.sum()等于3.9999999999999987而不是4,是由于浮点数的存储方式,在某些情况下,计算机无法精确表示某些小数。所以此计算步骤为[2.89312513/3.9999999999999987, 0.15504989/3.9999999999999987]得到[0.72328128 0.03876247],也就是每个主成分在总方差中的方差解释比例。
相关文章:

使用python求PLS-DA的方差贡献率
以鸢尾花数据集为例,实现PLS-DA降维,画出降维后数据的散点图并求其方差贡献率。 效果图 完整代码 # 导入所需库 import numpy as np from sklearn.cross_decomposition import PLSRegression from sklearn.datasets import load_iris from sklearn.pre…...

前端面试题--JavaScript篇
一、JavaScript中的数据类型JavaScript中共有八种数据类型:Number、String、Boolean、Object、Null、Undefined、null、Symbol、BigInt 其中Symbol和BigInt是ES6新增的数据类型Symbol代表独一无二且不可改变的数据类型,主要为了解决可能出现的全局变量冲…...

【批处理脚本】-3.5-pause暂停命令详解
"><--点击返回「批处理BAT从入门到精通」总目录--> 共3页精讲(列举了所有pause的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...
软件测试11
一 Linux命令的基本格式 格式组成:命令主体 -命令选项 命令参数 常见命令形式: (1)命令主体 (2)命令主体 -命令选项 (3)命令主体 参数 (4)命令主体 -命令选项…...

2023 面试题js、es6篇
什么是闭包? 闭包的定义 闭包是指能够访问另一个函数作用域中的变量的一个函数。 在js中,只有函数内部的子函数才能访问局部变量, 所以闭包可以理解成 “定义在一个函数内部的函数”。 应用场景 将内部的函数返到外部去,让外部…...
设计索引的时候,我们一般要考虑哪些因素呢?(下))
(六十六)设计索引的时候,我们一般要考虑哪些因素呢?(下)
今天我们最后来讲一下设计索引的时候,我们一般要考虑哪些因素。 另外还讲了字段基数的问题以及前缀索引的问题, 那么今天接着来讲剩下的一些索引设计的原则。 首先假设你设计好了一个索引,非常棒,接着你在SQL里这么写ÿ…...
python程序设计基础 实验四
⭐python实验专栏,欢迎订阅与关注! ★观前提示:本篇内容为python程序设计实验,代码内容经测试没有问题,但是可能会不符合每个人实验的要求,因此以下内容建议仅做思路参考。 一、实验目的 (1&am…...
ASP.NET CORE API 使用Orleans
快速使用Monimal API 快速集成Orleans 微软官网地址如下:https://learn.microsoft.com/zh-cn/dotnet/orleans/quickstarts/build-your-first-orleans-app?sourcerecommendations&tabsvisual-studio当然它的存储grain存储采用的是内存级别存储,我缓存…...
)
《论文阅读》软化标签(将one-hot编码转变为grayscale标签)
《论文阅读》The Emotion is Not One-hot Encoding: Learning with Grayscale Label for Emotion Recognition in Conversation 前言简介相关知识grayscale label模型方法CategoryWord-EmbeddingSelfSelf-AdjustFuture-Self损失实验结果前言 你是否也对于理解论文存在困惑? …...
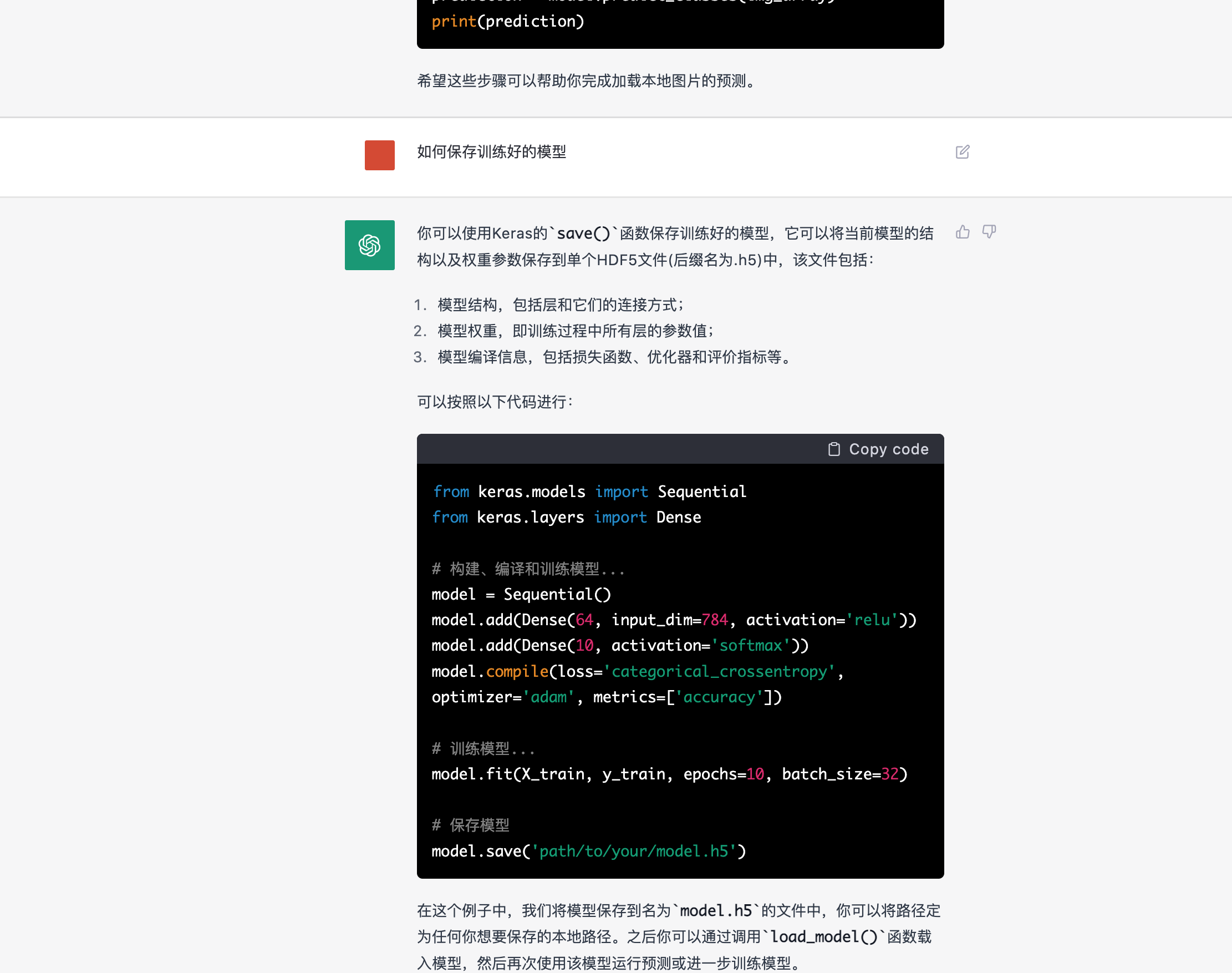
keras图片数字识别入门AI机器学习
通过使用mnist(AI界的helloworld)手写数字模型训练集,了解下AI工作的基本流程。 本例子,要基于mnist数据集(该数据集包含了【0-9】的模型训练数据集和测试数据集)来完成一个手写数字识别的小demo。 mnist…...

使用qt编写一个程序,伪造一个ip访问一个网站。
你好,这是Bing。😊 根据网络搜索结果,使用qt编写一个程序,伪造一个ip访问一个网站的方法可能有以下几种: - 使用X-Forwarded-For请求头来伪造客户端的真实ip地址。这种方法需要在发送请求时添加X-Forwarded-For: 伪造…...

探访人工智能领跑者:纷享销客携手30+TOP高科技企业走进旷视科技
拥有全球规模领先的计算机视觉研究院; 揽获28项世界顶级AI竞赛冠军; 世界级人工智能公司; 没错,它就是人工智能行业的务实者和领跑者,旷视科技。 3月3日,北京软件和信息服务业协会联合纷享销客,…...

UTC、TimeZone、TimeStamp
UTC :Universal Time Coordinated,世界协调时,又称世界标准时间。与UTC time对应的是各个时区的local time,东N区的时间比UTC时间早N个小时,因此UTC time N小时 即为东N区的本地时间;而西N区时间比UTC时间…...
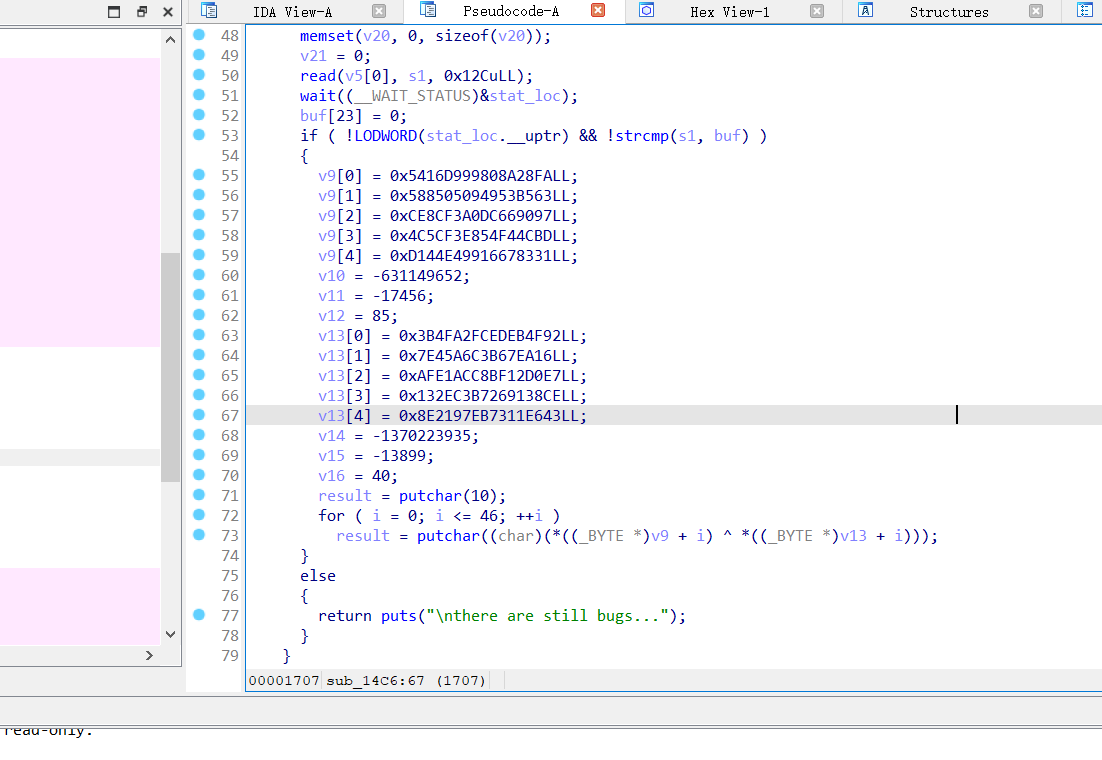
探究SMC局部代码加密技术以及在CTF中的运用
前言 近些日子在很多线上比赛中都遇到了smc文件加密技术,比较出名的有Hgame杭电的比赛,于是我准备实现一下这项技术,但是在网上看了很多文章,发现没有讲的特别详细的,或者是无法根据他们的方法进行实现这项技术,因此本篇文章就是…...

免费集装箱箱号识别API,人工智能企业CIMCAI集装箱识别检测人工智能平台全球4千企业用户,支持API集成二次开发人工智能企业
免费集装箱箱号识别API,人工智能企业CIMCAI集装箱识别检测人工智能平台全球4千企业用户,支持API集成二次开发。箱信息识别及铅封号识别功能免费,顶尖AI集装箱识别率99.98%,全球No.1集装箱人工智能企业CIMCAI打造。中国上海人工智能…...
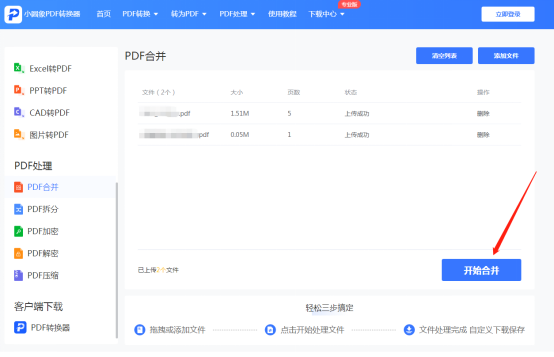
pdf多页合并为一页方法总结,你觉得哪个最好?
PDF格式的文件在现代办公中是不可或缺的,许多人在工作中需要频繁处理PDF文档。然而,当我们需要阅读多个PDF文件时,不断切换不同的文件并一个一个地打开查阅会非常麻烦。为了提高阅读效率,人们一般会将pdf多页合并为一页。那么&…...

每日一读【基金/股票投资的常识和纪律】
个人投资的几点总结,我时常拿来阅读,警示自己: *基于常识,独立思考。 *投资以年为单位,5年一周期。 *下跌时的信心比金子还贵,永远要记住:风险是涨上去的,机会…...

阶段二12_面向对象高级_继承3
知识点内容: 抽象类 模板设计模式 final关键字 一.抽象类 (1)抽象类概述 抽象方法:将共性的行为(方法)抽取到父类之后,发现该方法的实现逻辑 无法在父类中给出具体明确,该方法就可以定义为抽象方法。 抽…...

C++ STL:string类的概述及常用接口说明
目录 一. 什么是STL 二. string类的概述 三. string类的常用接口说明 3.1 字符串对象创建相关接口(构造函数) 3.2 字符串长度和容量相关接口 3.3 字符访问相关接口函数 3.4 字符串删改相关接口函数 3.5 字符查找和子串相关接口函数 3.6 迭代器相…...
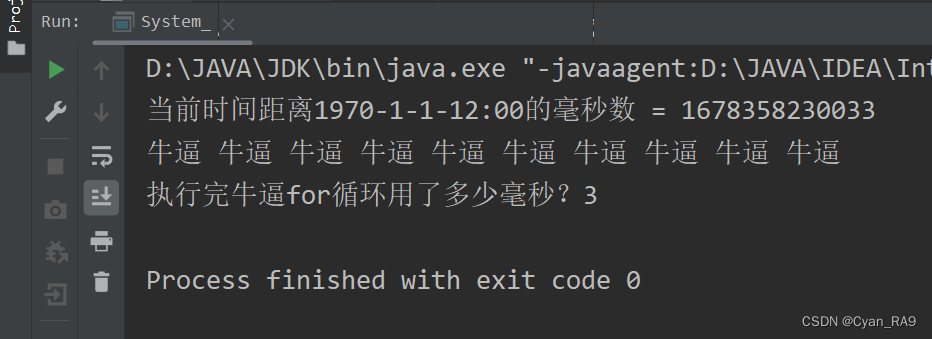
java Math类 和 System类 详解(通俗易懂)
Math类介绍Math类常用方法及演示System类简介System类常用方法及演示一、前言本节内容是我们《API-常用类》专题的第四小节了。本节内容主要讲Math类和System类, 内容包括Math类介绍、Math类常用方法、System类介绍,System类常用方法。该小节内容基本不涉…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
