2024.5.29晚训参考代码
因为本套题没有BFS例题,所以我先把BFS模板放着
#include<bits/stdc++.h>
using namespace std;
int n,m;//n*m的棋盘
int dis[402][402];
bool vis[402][402];
int X[]={-2,-2,-1,-1,1,1,2,2};//偏移量的表
int Y[]={-1,1,-2,2,-2,2,-1,1};//定义一个数组,我直接把这些元素从0位置填充进去
struct node{int x;int y;int dis;//从起点走到当前(x,y)的最短步数
};
int st,ed;//起点x y坐标
void bfs(){ queue<node>q;node now;now.x=st;now.y=ed;now.dis=0;q.push(now);//放入队列,第一个搜索的状态 dfs(st,ed,0) while(!q.empty()){//第一步取出队首状态//第二步,弹出队首 //第三步 判断当前状态是不是已经走过了 后面再来到这个点肯定不是最短距离//仅限于所有距离都一样的情况 //第四步 判断当前的点是不是终点 //第五步 打标记//第六步 做相关的数据统计 比如记录(now.x,now.y)的最小步数 //第七步 以这个点拓展出去的其余状态 注意判断非法情况 }//bfs结束
}
signed main(){int x,y;cin>>n>>m;cin>>st>>ed;//memset(dis,-1,sizeof(dis));//初始化数组 for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dis[i][j]=1e9;//表示不可到达 }}//dis[i][j]表示从起点走到(i,j)的最短距离 bfs();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){// dis[i][j]=1e9;//表示不可到达 if(dis[i][j]==1000000000)cout<<-1;else cout<<dis[i][j];cout<<" ";}cout<<'\n';}return 0;
}马的便利
#include<bits/stdc++.h>
using namespace std;
struct node{int x;int y;int dis;//从起点走到(x,y)的距离
};
int n,m,x,y;
int X[]={-1,-1,-2,-2,1,1,2,2};
int Y[]={2,-2,-1,1,2,-2,1,-1};
int dis[405][405];
int vis[405][405];
void bfs(){queue<node>q;node now;now.x=x;now.y=y;now.dis=0;q.push(now);while(!q.empty()){node now=q.front();q.pop();if(vis[now.x][now.y]==1){continue;//已经走过这个点了 }dis[now.x][now.y]=now.dis;vis[now.x][now.y]=1;node cnt;for(int i=0;i<8;i++){cnt.x=now.x+X[i];cnt.y=now.y+Y[i];cnt.dis=now.dis+1;if(cnt.x<1||cnt.x>n||cnt.y<1||cnt.y>m)continue;q.push(cnt);}}
}
int main(){cin>>n>>m>>x>>y;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dis[i][j]=-1;}}bfs();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<dis[i][j]<<" ";}cout<<'\n';}return 0;
}
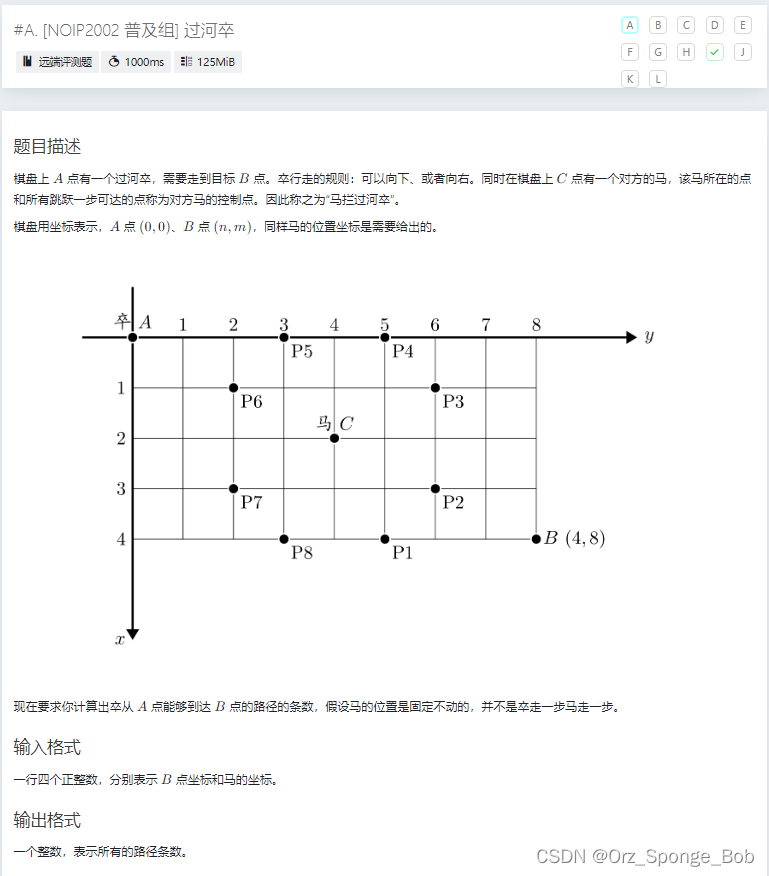
需要考虑记忆化处理
#include<bits/stdc++.h>
using namespace std;
#define int long long
int vis[30][30];
int n,m,s,b;
int dfs(int x,int y){if(x<0||y<0)return 0;if((x==s&&y==b)||(x==s-1&&y==b-2)||(x==s-2&&y==b-1)||(x==s-2&&y==b+1))return 0;if((x==s-1&&y==b+2)||(x==s+1&&y==b+2)||(x==s+2&&y==b+1)||(x==s+2&&y==b-1)||(x==s+1&&y==b-2))return 0;if(x==0&&y==0)return 1;if(vis[x][y])return vis[x][y];return vis[x][y]=dfs(x-1,y)+dfs(x,y-1);
}
signed main() {cin>>n>>m>>s>>b;cout<<dfs(n,m);return 0;
}
#include<bits/stdc++.h>
using namespace std;
char A[1005];
char B[1005];
int dp[1005][1005];
int main(){int n,m;cin>>n>>m;cin>>A+1>>B+1;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(A[i]==B[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j-1],max(dp[i-1][j],dp[i][j-1]));}}}cout<<dp[n][m];return 0;
}
#include<bits/stdc++.h>
using namespace std;
long long dp[100005][2];
int main() {int n;cin>>n;//dp[0][0]=dp[0][]//dp[i][0] 没抢i银行 for(int i=1;i<=n;i++){long long x;cin>>x;
// cout<<i<< " ";dp[i][0]=max(dp[i-1][0],dp[i-1][1]);//没抢 dp[i][1]=dp[i-1][0]+x;
// cout<<dp[i][0]<<" "<<dp[i][1]<<'\n';}cout<<max(dp[n][0],dp[n][1]);return 0;
}
物品只拿一次,01背包
#include<bits/stdc++.h>
using namespace std;
int V[1005],W[1005];//
int dp[1005];
//有一大堆财宝,体积分别是V[i] 价值是W[i]
//你现在有一个体积为M的包,你想知道怎么样拿 能保证 在背包容量的限制下 拿到最多价值的财宝
signed main(){//总背包容量10 //只考虑拿价值高的 价值是10,体积是10 可能有其他财宝价值5 体积1 有若干个 //dfs(拿/不拿) 暴力 n<=20 /*背包dp 01背包 dp[i][j] 表示处理完前i个物品 有j的容量 单独考虑处理第i个物品,那么是不是跟dp[i-1][] + 如何处理第i个物品=> dp[i][] 有关联 如果第i个物品你要拿 因为你拿了第i个物品,体积变大,变成了dp[i][j] dp[i][j] = dp[i-1][j-V[i]] + W[i] 如果我们不拿第i个物品 变到了dp[i][j] dp[i][j] =dp[i-1][j] ?????我们的容量j dp[i][j] =max(dp[i-1][j],dp[i-1][j-V[i]]+W[i]); // j=?+V[i] */int M,n;cin>>M>>n;//M是总体积 n是物品个数 for(int i=1;i<=n;i++){cin>>V[i]>>W[i];//输入体积 和 价值 }for(int i=1;i<=n;i++){for(int j=M;j>=V[i];j--){dp[j]=max(dp[j],dp[j-V[i]]+W[i]);}}cout<<dp[M];return 0;
}
#include<bits/stdc++.h>
using namespace std;
long long T,M,t[10001],v[10001],dp[10000001];
int main(){cin>>T>>M;for(int i=1;i<=M;i++)cin>>t[i]>>v[i];for(int i=1;i<=M;i++)for(int j=t[i];j<=T;j++)dp[j]=max(dp[j],dp[j-t[i]]+v[i]);cout<<dp[T];return 0;
}
#include<bits/stdc++.h>
using namespace std;
int dp[305][305];
int w[305];
int sum[305];
signed main(){/* 考虑区间dp dp[l][r]= 表示把[L,R]的石头合并成一堆所需要的最小花费 考虑转移1 1 1 1 1 1 1所有大的区间一定由小区间转移 考虑合并成长度为2的区间// dp[i][i+1]=(dp[i][i]+dp[i+1][i+1])+w[i]+w[i+1] 合并成3区间 来自于长度为2 + 拼长度为1 长度为4的区间 1+3 2+2 3+1 .... 考虑dp[l][r] 拆成两个区间,进行合并 */int n;cin>>n;for(int i=1;i<=n;i++){cin>>w[i];sum[i]=sum[i-1]+w[i];//前缀和 }for(int len=1;len<=n;len++){ for(int i=1;i<=n;i++){//i作为区间起点//枚举区间长度//计算右端点在哪int j=i+len;dp[i][j]=1e9;if(j>n)break; for(int k=i;k<j;k++){dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);}} } cout<<dp[1][n];return 0;
}
#include<bits/stdc++.h>
using namespace std;
int n;
int minx = 0x3f3f3f3f,maxn = -1;
int s[305];
int m[305];
int dp1[305][305];
int dp2[305][305];
int main()
{cin >> n;for(int i = 1; i <= n; i++){cin >> m[i];m[i + n] = m[i];}memset(dp1,0x3f3f3f3f,sizeof(dp1));memset(dp2,-1,sizeof(dp2));for(int i = 1; i <= n * 2; i++){s[i] = s[i - 1] + m[i];dp1[i][i] = 0;dp2[i][i] = 0;}for(int i = 2; i <= n; i++){for(int l = 1; l <= n * 2 - i + 1; l++){int r = l + i - 1;for(int j = l; j < r; j++){dp1[l][r] = min(dp1[l][r],dp1[l][j] + dp1[j + 1][r]);dp2[l][r] = max(dp2[l][r],dp2[l][j] + dp2[j + 1][r]);}dp1[l][r] += (s[r] - s[l - 1]);dp2[l][r] += (s[r] - s[l - 1]);}}for(int i = 1; i <= n; i++){minx = min(minx,dp1[i][i + n - 1]);maxn = max(maxn,dp2[i][i + n - 1]);}cout << minx << "\n" << maxn;return 0;
}
注意输出格式啊。。。。注意数据类型 long long
#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1005][1005];
long long sum[1005][1005];
int main() {cin >> n >> m;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {cin >> a[i][j];}}for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++) {sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];}}int q; cin >> q;while(q--) {int X1, Y1, X2, Y2;cin >> X1 >> Y1 >> X2 >> Y2;cout << sum[X2][Y2] - sum[X1 - 1][Y2] - sum[X2][Y1 - 1] + sum[X1 - 1][Y1 - 1] << '\n';}return 0;
}

#include<bits/stdc++.h>
using namespace std;
int a[100005];
long long int pre[100005];
long long int sum[100005];
int main()
{int n;scanf("%d",&n);for(int i=1; i<=n; i++){scanf("%d",&a[i]);pre[i]=a[i]-a[i-1];}//1 2 3 4 5
//+2 -2
//+3 -3int m;scanf("%d",&m);while(m--){int l,r,x;scanf("%d%d%d",&l,&r,&x);pre[l]+=x;pre[r+1]-=x;}int st,ed;scanf("%d%d",&st,&ed);long long int ans=0;long long int cnt=0;for(int i=1;i<=n;i++){sum[i]=sum[i-1]+pre[i];}for(int i=st; i<=ed; i++){ans+=sum[i];}printf("%lld",ans);}

#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define all(x) x.begin(),x.end()
using namespace std;
const double eps=1e-8;
const double PI=acos(-1.0);
typedef long long ll;
template<class T>int chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>int chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
int a[1024][1024];
int main(){
#ifdef cnyali_lkfreopen("in.txt","r",stdin);freopen("out.txt","w",stdout);
#endifint n,m,xa,ya,xb,yb;scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d%d%d%d",&xa,&ya,&xb,&yb);++a[xa][ya];--a[xb+1][ya];--a[xa][yb+1];++a[xb+1][yb+1];}for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)printf("%d%c",a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1],j==n?'\n':' ');return 0;
}
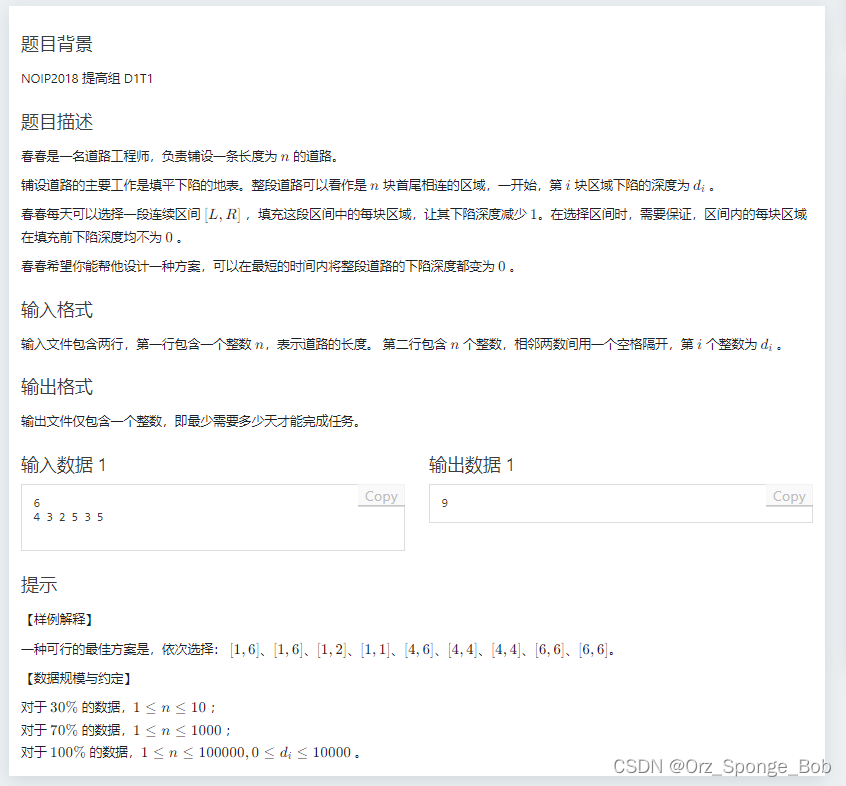
答案 A【1】+ 枚举i=2~n 里面所有的A[i]>A[i-1] 的情况的差
相关文章:

2024.5.29晚训参考代码
因为本套题没有BFS例题,所以我先把BFS模板放着 #include<bits/stdc.h> using namespace std; int n,m;//n*m的棋盘 int dis[402][402]; bool vis[402][402]; int X[]{-2,-2,-1,-1,1,1,2,2};//偏移量的表 int Y[]{-1,1,-2,2,-2,2,-1,1};//定义一个数组&…...
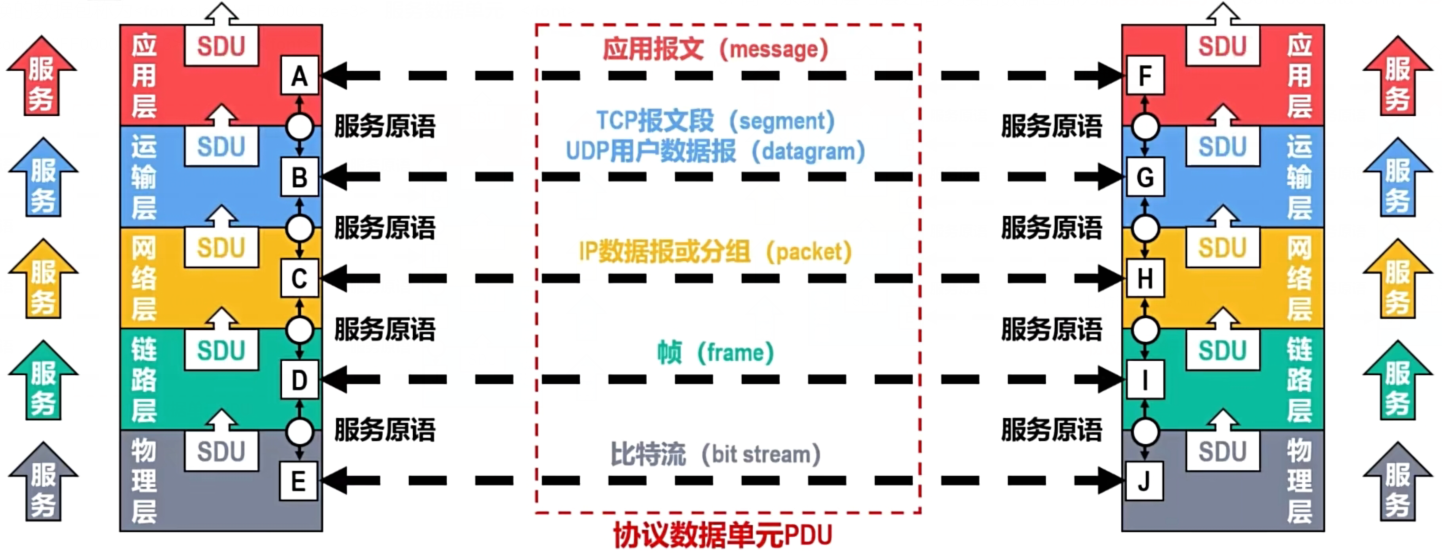
【计算机网络】——概述(图文并茂)
概述 一.信息时代的计算机网络二.互联网概述1.网络,互连网,互联网(因特网)1.网络2.互连网3.互联网(因特网) 2.互联网简介1.互联网发展的三个阶段2.互联网服务提供者(ISP)3.互联网的组…...
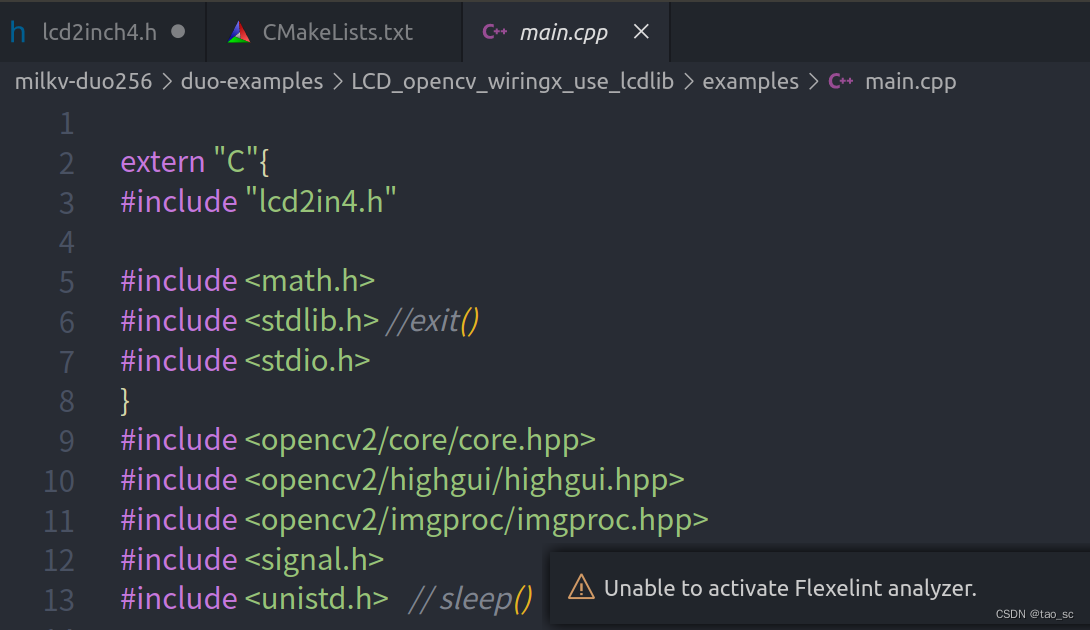
C语言多个源程序编译的CMakeList文件编写/源程序生成动态库
1.编译多个源程序时CMakeLists文件编写 1.若源程序目录结构如下: main.cpp中include“LCD_2inch4.h”头文件,而LCD_2inch4.h中include其它源程序,则CmakeLists.txt文件可为如下: # 设置项目名称 cmake_minimum_required(VERSI…...

C# list集合
一、list集合基本使用 1.添加元素 ① 单个元素添加 List<int> list new List<int>();for (int i 0; i < 3; i){list.Add(i);}//输出:0,1,2 ②初始化时添加元素 List<int> list2 new List<int> { 1, 2, 3 };//输出:0,1…...

****三次握手和四次挥手
一、三次握手 1.简要描述TCP三次握手的过程 第一次握手,客户端发送SYN包到服务器; 第二次握手,服务器收到SYN包,回复一个SYNACK包; 第三次握手,客户端收到服务器的SYNACK包后,回复一个ACK包…...
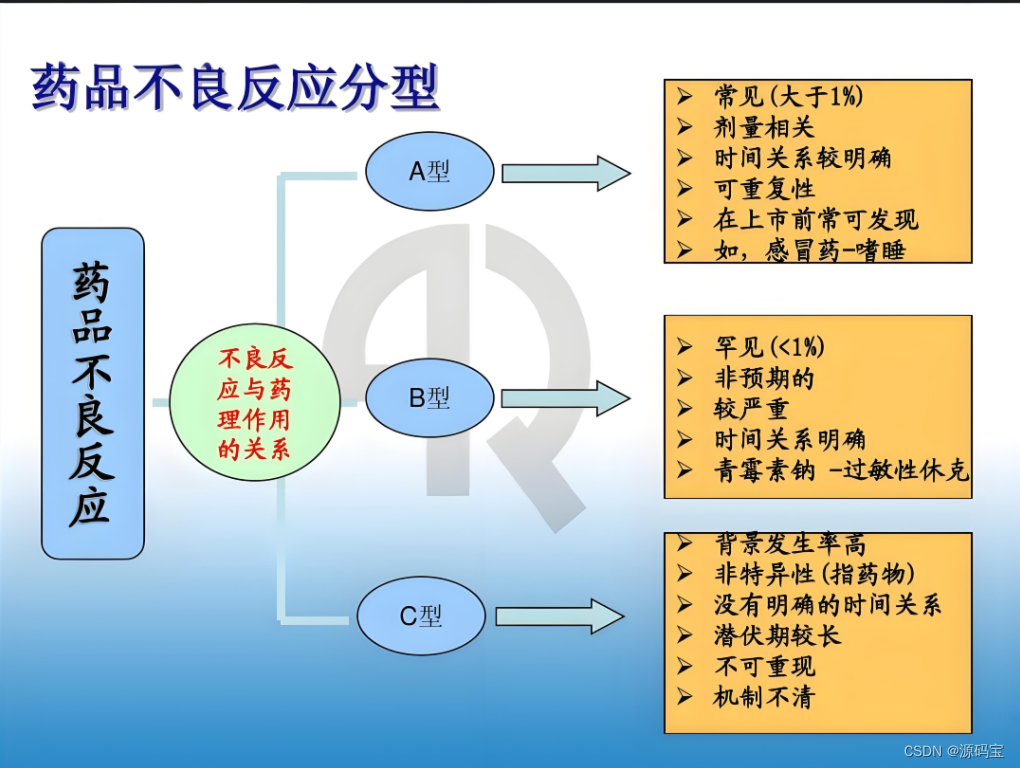
开发语言Java+前端框架Vue+后端框架SpringBoot开发的ADR药物不良反应监测系统源码 系统有哪些优势?
开发语言Java前端框架Vue后端框架SpringBoot开发的ADR药物不良反应监测系统源码 系统有哪些优势? ADR药物不良反应监测系统具有多个显著的优势,这些优势主要体现在以下几个方面: 一、提高监测效率与准确性: 通过自动化的数据收集…...
))
问题排查|记录一次基于mymuduo库开发的服务器错误排查(段错误--Segmentation fault (core dumped))
问题记录: 在刚完成mymuduo库之后,写了一个简单的测试服务器, 但是在服务器运行后直接报错: cherryhcss-ecs-4995:~/mymuduo/example$ ./testserver Segmentation fault (core dumped)出现多错误这通常意味着程序试图访问其内存空…...

Mysql常用操作DQL数据库、表操作:
DQL是指MySQL数据库中的数据查询语言(Data Query Language)。它是用来从数据库中检索所需数据的语言。DQL允许用户通过指定查询条件和筛选条件来检索数据库中的数据,并以所需的方式来显示结果。DQL语句可以用于从单个表中查询数据,…...

标题:Go语言中的YAML魔法:轻松配置你的环境
摘要: 本文将介绍如何在Go语言项目中使用YAML文件来管理配置,包括如何读取YAML文件以及如何在代码中解析和使用这些配置。 正文: 在编程世界中,配置管理是每个项目都必须面对的问题。对于Go语言项目来说,YAML文件是一…...
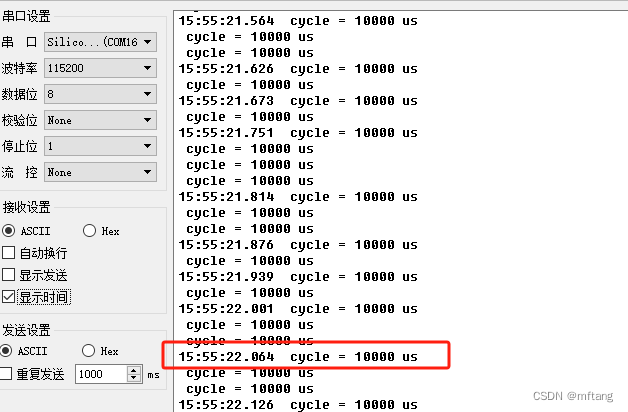
STM32高级控制定时器之输入捕获模式
目录 概述 1 输入捕获模式 1.1 原理介绍 1.2 实现步骤 1.3 发生输入捕获流程 2 使用STM32Cube配置工程 2.1 软件环境 2.2 配置参数 2.3 生成项目文件 3 功能实现 3.1 PWM调制占空比函数 3.2 应用函数库 4 测试 4.1 功能框图 4.2 运行结果 源代码下载地址…...

使用 Vue 3 和 qrcode.js 开发二维码显示组件
二维码在现代应用中广泛使用,例如支付、身份验证、链接分享等。本文将介绍如何使用 Vue 3 和 qrcode.js 库来创建一个灵活的二维码显示组件,并展示如何在应用中使用它。 1. 安装必要的依赖 首先,我们需要安装 Vue 3 和 qrcode.js。如果你还…...
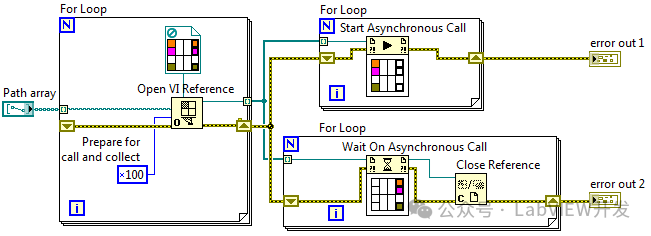
LabVIEW异步编程概述
LabVIEW异步编程是一种在图形化编程环境中处理并行任务的方法。通过异步执行,可以提高程序的响应速度和资源利用效率,使得多个任务可以独立进行而不互相干扰。 原理 LabVIEW异步编程的核心在于使用异步调用节点(Asynchronous Call By Refer…...
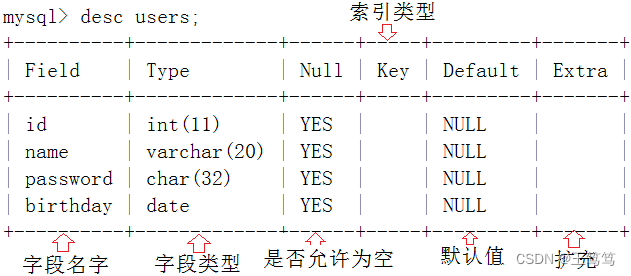
【数据库】MySQL表的操作
目录 一.创建表 二.查看表 三.修改表 四.删除表 一.创建表 基本语法: CREATE TABLE table_name(field1 datatype,field2 datatype,field3 datatype) character set 字符集 collate 校验规则 engine 储存引擎field表示列名 datatype表示列的类型 charatcer se…...

【mybatis解决oracle查询in超过1000条数据】
1、因为代码中前人未考虑in 数据可能大于1000,导致现在系统报错,MPP low前人 直接上sql select * from table a <where><if test"list ! null and list.size > 0">and a.name in<foreach collection"list" inde…...

EasyExcel之动态表头导出不生效
今天接到一个优化需求,表格导出后的表头顺序和页面不一致,要优化成一致的。根据传入的字段,动态导出数据,并保证顺序。 我看到导出的实体类都有ExcelProperty注解,同时也在官网查看了这注解的含义和使用。 ExcelPrope…...
appium元素定位工具_uiautomatorviewer.bat
特点: uiautomatorviewer是android-sdk自带的元素定位工具uiautomatorviewer只能用于安卓系统;它是通过截屏分析XML布局文件方式,来提供控件信息的查看服务 uiautomatorviewer.bat 基本使用 路径:这个工具是Android SDK中自带&…...
手机离线翻译哪个好?断网翻译也能超丝滑
有时在异国他乡,面对语言不通的窘境,即便是简单的对话也变得异常困难,真是挑战满满! 然而,能离线翻译的软件让语言障碍不再是问题,不必依赖网络也能轻松进行翻译啦~ 只需下载所需的语言包,选择…...

神器!!Python热重载调试【送源码】
在 Python 开发的路上,调试是我们不可避免的一环。 而今天推荐的开源项目Reloadium ,让你在不重启程序的情况下实现代码的即时更新和调试。 🔄 Reloadium 功能亮点: 1. 热重载魔法: Reloadium 不仅仅能够实现代码的…...
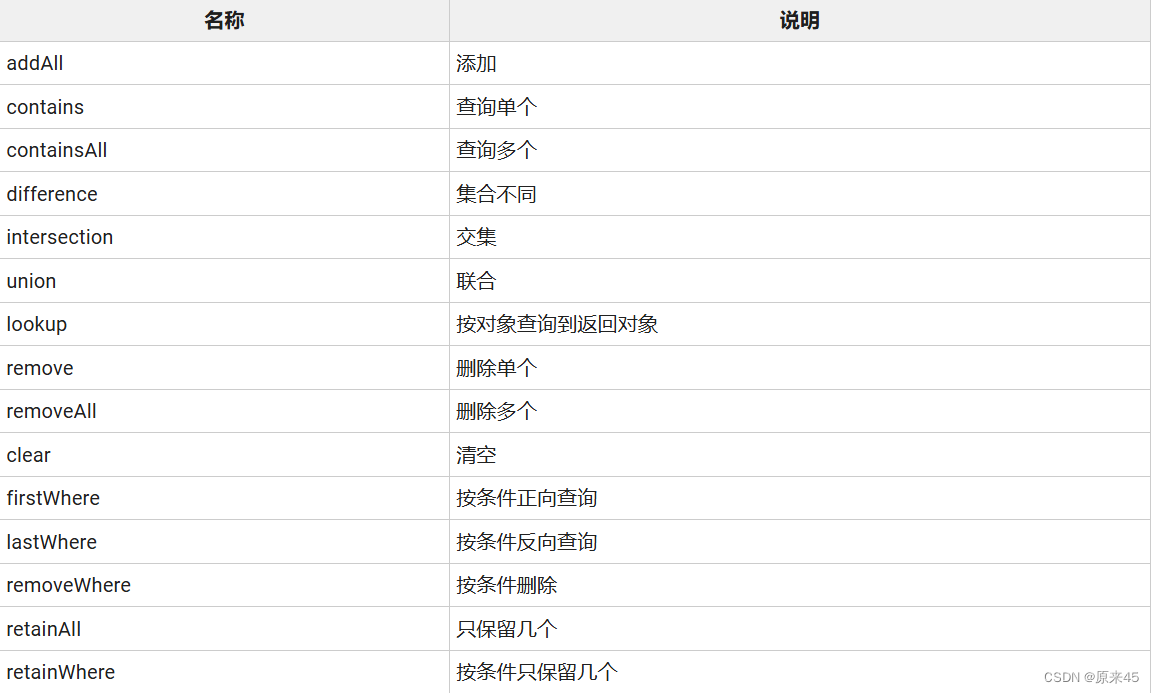
Flutter基础 -- Dart 语言 -- 列表集合枚举
目录 1. 列表 List 1.1 初始 1.2 声明 1.2.1 自动 1.2.2 定长 1.2.3 生成数据 1.3 属性 1.4 方法 1.4.1 添加 1.4.2 查询 1.4.3 删除 1.4.4 Range 1.4.5 洗牌 1.4.6 排序 1.4.7 复制子列表 1.4.8 操作符 2. 集合 Map 2.1 初始 2.2 声明 2.2.1 松散 2.2.2 …...

怎么花草识别?方法有三种!
怎么花草识别?在这个五彩斑斓的世界里,花草是我们生活中不可或缺的一部分。它们点缀着我们的环境,为我们带来无尽的美丽与惊喜。然而,面对众多的花草种类,你是否曾感到困惑和迷茫,不知道如何识别它们&#…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
