数据结构 | 二叉树(基本概念、性质、遍历、C代码实现)
1.树的基本概念

2.二叉树的基本概念
2.1特殊的二叉树
满二叉树
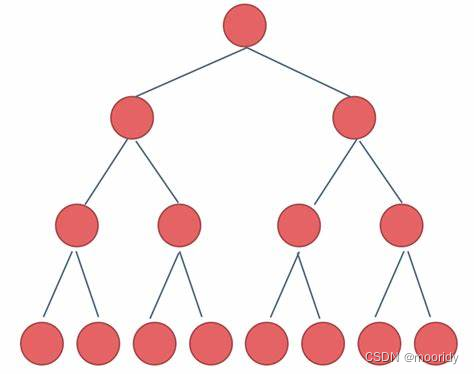
完全二叉树

3.二叉树的性质
4 .二叉树的存储结构
5.二叉树的遍历
5.1 前序、中序以及后序遍历
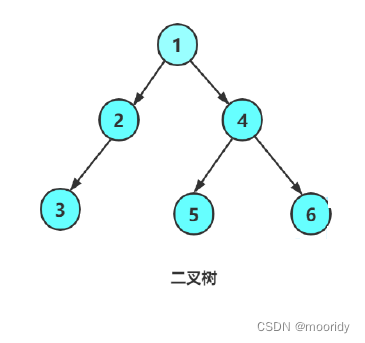
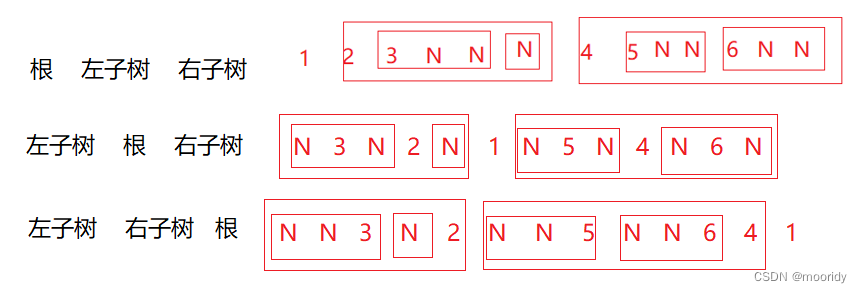
5.2 层序遍历
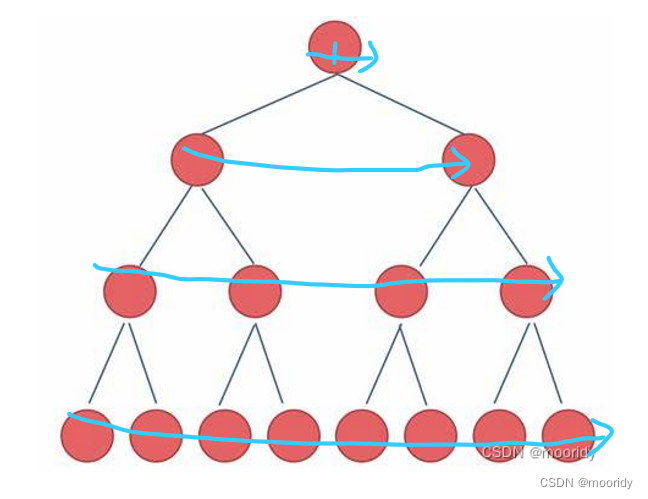

6.二叉树代码实现
思路
前序/中序/后序遍历
递归思想:将当前的大问题拆解成小问题
以前序遍历为例:
当前问题——打印根,打印左子树,打印右子树
子问题——如图
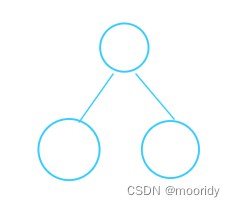
递归返回条件——root==NULL
前序遍历代码
//前序遍历 根节点 左节点 右节点
void BinaryTreePrevOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}中序遍历代码
void BinaryTreeInOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}后序遍历代码
void BinaryTreePostOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}节点个数/叶子节点个数/树高/第k层叶子数
1.节点个数
递归思想:
情况1:空,0个
情况2:不为空,左子树+右子树+1
2.叶子节点个数
情况1:空,返回0
情况2:只有一个结点,返回1
情况3:左子树+右子树
3.树的高度
情况1:空,返回0
情况2:左子树和右子树高度中大的值+1
4.第k层叶子数
情况1:空,返回0
情况2:非空,k==1,返回1
情况3:非空,k>1,左子树第k-1层+右子树第k-1层
int BinaryTreeSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}int BinaryTreeLeafSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}int BinaryTreeLevelKSize(BTNode* root, int k) {if (root == NULL) {return 0;}if (k==1) {return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}查找值为x的节点
递归思想
情况1:空,返回NULL
情况2:不为空,根值为x,返回根节点
情况3:不为空,根值不为x,查找左子树,有则返回
左子树中无,查找右子树,有则返回
右子树中也无,返回空
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {BTNode* ret = NULL;if (root == NULL) {return NULL;}if (root->data == x) {ret = root;return ret;}if (BinaryTreeFind(root->left, x) != NULL) {ret = BinaryTreeFind(root->left, x);}if (BinaryTreeFind(root->right, x) != NULL) {ret = BinaryTreeFind(root->right, x);}
}
层序遍历/完全二叉树
层序遍历
1.根进队列
2.节点出队列时,该节点的子节点(非空)进队列
3.当队列为空时,循环结束
完全二叉树
1.进行层序遍历,空也进队列
2.遇到第一个空节点,开始判断,后面全空就是完全二叉树,后面有非空就不是完全二叉树
void BinaryTreeLevelOrder(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head->left) {QueuePush(&q, head->left);}if (head->right) {QueuePush(&q, head->right);}printf("%d", head->data);QueuePop(&q);}QueueDestroy(&q);
}bool BinaryTreeComplete(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head == NULL) {break;}QueuePush(&q, head->left);QueuePush(&q, head->right);QueuePop(&q);}while(!QueueEmpty(&q)){BTNode* head = QueueFront(&q);if (head) {QueueDestroy(&q);return false;}QueuePop(&q);}QueueDestroy(&q);return true;
}代码汇总
binarytree.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate();
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
binarytree.c
#define _CRT_SECURE_NO_WARNINGS
#include "binarytree.h"
#include "queue.h"BTNode* BuyNode(BTDataType x) {BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL) {perror("malloc fail!");}newnode->left = NULL;newnode->right = NULL;newnode->data = x;return newnode;
}BTNode* BinaryTreeCreate() {BTNode* Node1 = BuyNode(1);BTNode* Node2 = BuyNode(2);BTNode* Node3 = BuyNode(3);BTNode* Node4 = BuyNode(4);BTNode* Node5 = BuyNode(5);BTNode* Node6 = BuyNode(6);BTNode* Node7 = BuyNode(7);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;//Node6->left = Node7;return Node1;//返回根节点
}
//前序遍历 根节点 左节点 右节点
void BinaryTreePrevOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}void BinaryTreeInOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}void BinaryTreePostOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}int BinaryTreeSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}int BinaryTreeLeafSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}int BinaryTreeLevelKSize(BTNode* root, int k) {if (root == NULL) {return 0;}if (k==1) {return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {BTNode* ret = NULL;if (root == NULL) {return NULL;}if (root->data == x) {ret = root;return ret;}if (BinaryTreeFind(root->left, x) != NULL) {ret = BinaryTreeFind(root->left, x);}if (BinaryTreeFind(root->right, x) != NULL) {ret = BinaryTreeFind(root->right, x);}
}void BinaryTreeLevelOrder(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head->left) {QueuePush(&q, head->left);}if (head->right) {QueuePush(&q, head->right);}printf("%d", head->data);QueuePop(&q);}QueueDestroy(&q);
}bool BinaryTreeComplete(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head == NULL) {break;}QueuePush(&q, head->left);QueuePush(&q, head->right);QueuePop(&q);}while(!QueueEmpty(&q)){BTNode* head = QueueFront(&q);if (head) {QueueDestroy(&q);return false;}QueuePop(&q);}QueueDestroy(&q);return true;
}void BinaryTreeDestory(BTNode* root) {if (root==NULL) {return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}在实现层序遍历时,会使用到队列。但由于C语言中没有现成的数据结构队列可以直接使用,需要自己实现。
queue.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef struct BinaryTreeNode* QDataType;typedef struct QListNode{struct QListNode* next;QDataType data;
}QNode;// 队列的结构
typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);queue.c
#define _CRT_SECURE_NO_WARNINGS
#include "queue.h"
// 初始化队列
void QueueInit(Queue* q) {assert(q);q->phead = q->ptail = NULL;q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data) {assert(q);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL) {perror("malloc fail!");exit(1);}else {newnode->data = data;newnode->next = NULL;if (q->ptail == NULL) {q->phead = q->ptail = newnode;q->size++;}else {q->ptail->next =newnode;q->ptail = newnode;q->size++;}}
}
// 队头出队列
void QueuePop(Queue* q) {assert(q);assert(q->size != 0);if (q->phead->next == NULL) {free(q->ptail);q->ptail = q->phead = NULL;q->size--;}else {QNode* next = q->phead->next;free(q->phead);q->phead = next;q->size--;}
}
// 获取队列头部元素
QDataType QueueFront(Queue* q) {assert(q);assert(q->size > 0);return q->phead->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q) {assert(q);assert(q->size > 0);return q->ptail->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q) {assert(q);return q->size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q) {assert(q);return !QueueSize(q);
}
// 销毁队列
void QueueDestroy(Queue* q) {assert(q);while (q->size) {QueuePop(q);}q->phead = NULL;q->ptail = NULL;
}7.堆及堆排序及TopK问题
详见我的另一篇文章~(TopK问题待更)
数据结构 | 详解二叉树——堆与堆排序
相关文章:

数据结构 | 二叉树(基本概念、性质、遍历、C代码实现)
1.树的基本概念 树是一种 非线性 的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点,称为根…...

很多Oracle中的SQL语句在EF中写不出来
很多复杂的Oracle SQL语句在Entity Framework(EF)中很难直接表达出来。虽然EF提供了一种方便的方式来使用C#代码查询和操作数据库,但它在处理某些复杂的SQL特性和优化时可能会有局限性。 以下是一些在EF中可能难以直接实现的Oracle SQL功能和…...

浏览器打开PHP文件弹出下载而不是运行代码
说明 使用phpstudy,极少会出现这种情况。 这里主要是帮助大家理解,为什么上传的木马不运行。 问题原因 首先需要理解,访问PHP文件弹出下载,说明服务端的容器(比如Apache或者Nginx)把文件当成了一个普通二…...

安卓自定义UI组件开发流程
安卓自定义ui组件开发流程 开发安卓自定义UI组件的流程大致可以分为以下几个步骤: 确定需求和设计: 确定需要自定义的UI组件的功能和外观。设计组件的交互逻辑和视觉效果。 创建自定义组件类: 创建一个新的Java类,继承自View、V…...
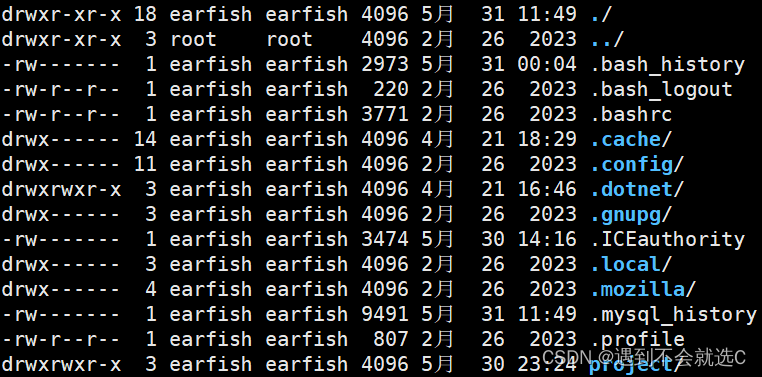
【LINUX】LINUX基础(目录结构、基本权限、基本命令)
文章目录 LINUX的目录结构LINUX的基本权限LINUX基本命令 LINUX的目录结构 /:表示根目录bin:存放二进制可执行文件(命令ls、cat、mkdir等)boot:存放系统引导文件dev:存放设备文件etc:存放系统配置文件home:…...

Aigtek功率放大器的主要性能要求有哪些
功率放大器是电子系统中的重要组件,用于将低功率信号放大到高功率水平。功率放大器的性能直接影响到信号的放大质量和系统的整体性能。下面西安安泰将介绍功率放大器的主要性能要求。 增益:功率放大器应当具有足够的增益,即将输入信号的幅度放…...
2024.5.29晚训参考代码
因为本套题没有BFS例题,所以我先把BFS模板放着 #include<bits/stdc.h> using namespace std; int n,m;//n*m的棋盘 int dis[402][402]; bool vis[402][402]; int X[]{-2,-2,-1,-1,1,1,2,2};//偏移量的表 int Y[]{-1,1,-2,2,-2,2,-1,1};//定义一个数组&…...
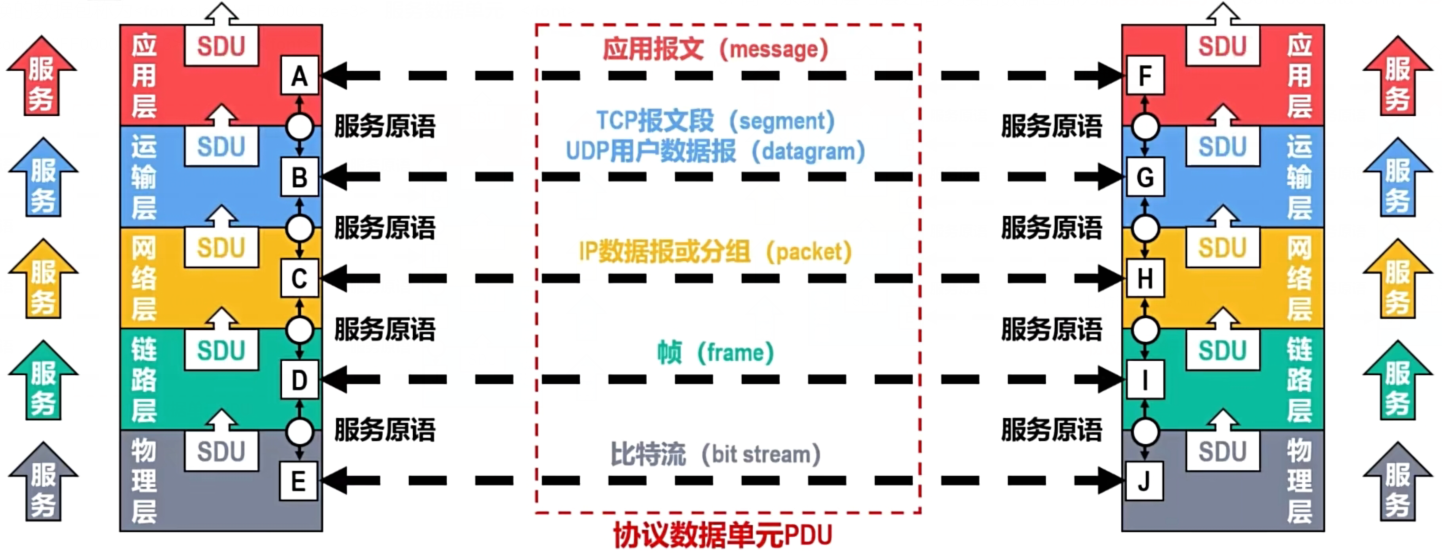
【计算机网络】——概述(图文并茂)
概述 一.信息时代的计算机网络二.互联网概述1.网络,互连网,互联网(因特网)1.网络2.互连网3.互联网(因特网) 2.互联网简介1.互联网发展的三个阶段2.互联网服务提供者(ISP)3.互联网的组…...
C语言多个源程序编译的CMakeList文件编写/源程序生成动态库
1.编译多个源程序时CMakeLists文件编写 1.若源程序目录结构如下: main.cpp中include“LCD_2inch4.h”头文件,而LCD_2inch4.h中include其它源程序,则CmakeLists.txt文件可为如下: # 设置项目名称 cmake_minimum_required(VERSI…...

C# list集合
一、list集合基本使用 1.添加元素 ① 单个元素添加 List<int> list new List<int>();for (int i 0; i < 3; i){list.Add(i);}//输出:0,1,2 ②初始化时添加元素 List<int> list2 new List<int> { 1, 2, 3 };//输出:0,1…...

****三次握手和四次挥手
一、三次握手 1.简要描述TCP三次握手的过程 第一次握手,客户端发送SYN包到服务器; 第二次握手,服务器收到SYN包,回复一个SYNACK包; 第三次握手,客户端收到服务器的SYNACK包后,回复一个ACK包…...
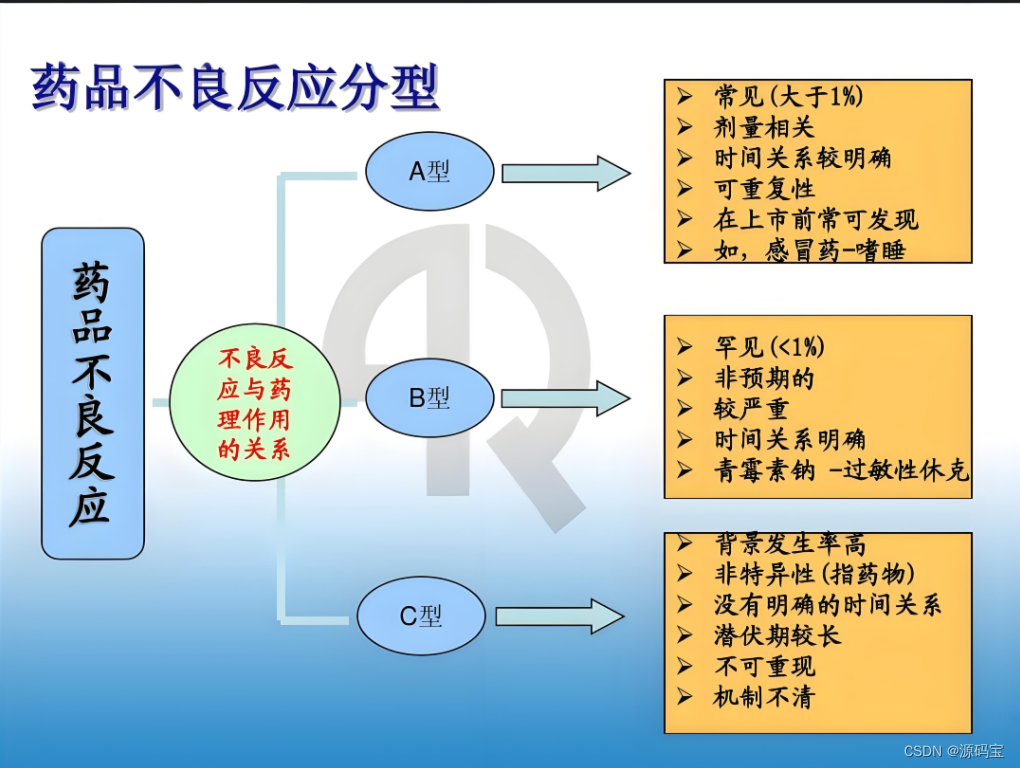
开发语言Java+前端框架Vue+后端框架SpringBoot开发的ADR药物不良反应监测系统源码 系统有哪些优势?
开发语言Java前端框架Vue后端框架SpringBoot开发的ADR药物不良反应监测系统源码 系统有哪些优势? ADR药物不良反应监测系统具有多个显著的优势,这些优势主要体现在以下几个方面: 一、提高监测效率与准确性: 通过自动化的数据收集…...
))
问题排查|记录一次基于mymuduo库开发的服务器错误排查(段错误--Segmentation fault (core dumped))
问题记录: 在刚完成mymuduo库之后,写了一个简单的测试服务器, 但是在服务器运行后直接报错: cherryhcss-ecs-4995:~/mymuduo/example$ ./testserver Segmentation fault (core dumped)出现多错误这通常意味着程序试图访问其内存空…...

Mysql常用操作DQL数据库、表操作:
DQL是指MySQL数据库中的数据查询语言(Data Query Language)。它是用来从数据库中检索所需数据的语言。DQL允许用户通过指定查询条件和筛选条件来检索数据库中的数据,并以所需的方式来显示结果。DQL语句可以用于从单个表中查询数据,…...

标题:Go语言中的YAML魔法:轻松配置你的环境
摘要: 本文将介绍如何在Go语言项目中使用YAML文件来管理配置,包括如何读取YAML文件以及如何在代码中解析和使用这些配置。 正文: 在编程世界中,配置管理是每个项目都必须面对的问题。对于Go语言项目来说,YAML文件是一…...
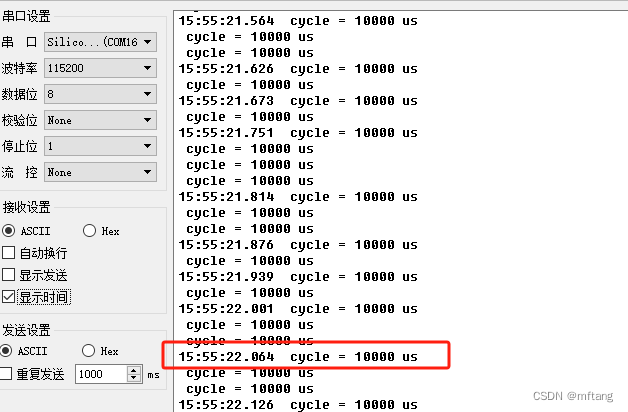
STM32高级控制定时器之输入捕获模式
目录 概述 1 输入捕获模式 1.1 原理介绍 1.2 实现步骤 1.3 发生输入捕获流程 2 使用STM32Cube配置工程 2.1 软件环境 2.2 配置参数 2.3 生成项目文件 3 功能实现 3.1 PWM调制占空比函数 3.2 应用函数库 4 测试 4.1 功能框图 4.2 运行结果 源代码下载地址…...

使用 Vue 3 和 qrcode.js 开发二维码显示组件
二维码在现代应用中广泛使用,例如支付、身份验证、链接分享等。本文将介绍如何使用 Vue 3 和 qrcode.js 库来创建一个灵活的二维码显示组件,并展示如何在应用中使用它。 1. 安装必要的依赖 首先,我们需要安装 Vue 3 和 qrcode.js。如果你还…...
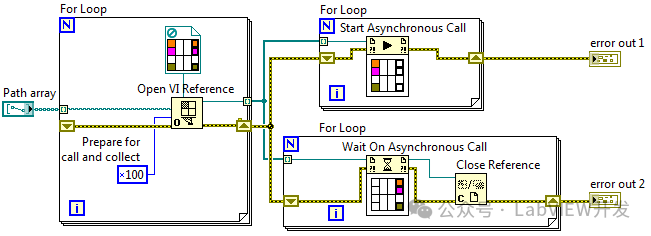
LabVIEW异步编程概述
LabVIEW异步编程是一种在图形化编程环境中处理并行任务的方法。通过异步执行,可以提高程序的响应速度和资源利用效率,使得多个任务可以独立进行而不互相干扰。 原理 LabVIEW异步编程的核心在于使用异步调用节点(Asynchronous Call By Refer…...
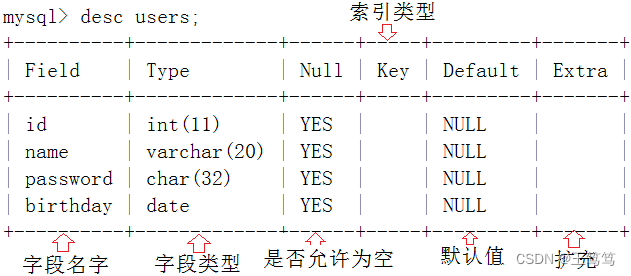
【数据库】MySQL表的操作
目录 一.创建表 二.查看表 三.修改表 四.删除表 一.创建表 基本语法: CREATE TABLE table_name(field1 datatype,field2 datatype,field3 datatype) character set 字符集 collate 校验规则 engine 储存引擎field表示列名 datatype表示列的类型 charatcer se…...

【mybatis解决oracle查询in超过1000条数据】
1、因为代码中前人未考虑in 数据可能大于1000,导致现在系统报错,MPP low前人 直接上sql select * from table a <where><if test"list ! null and list.size > 0">and a.name in<foreach collection"list" inde…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

