5.23R语言-参数假设检验
理论
方差分析(ANOVA, Analysis of Variance)是统计学中用来比较多个样本均值之间差异的一种方法。它通过将总变异分解为不同来源的变异来检测因子对响应变量的影响。方差分析广泛应用于实验设计、质量控制、医学研究等领域。
方差分析的基本模型
方差分析的基本模型可以用以下形式表示:

单因素方差分析
单因素方差分析(One-Way ANOVA)是最简单的形式,用于比较一个因素的多个水平对结果的影响。例如,比较不同肥料对作物生长的影响。
步骤:
1.假设检验:

2.计算组间方差和组内方差:
组间方差(MSB,Mean Square Between groups):

组内方差(MSW,Mean Square Within groups):↳
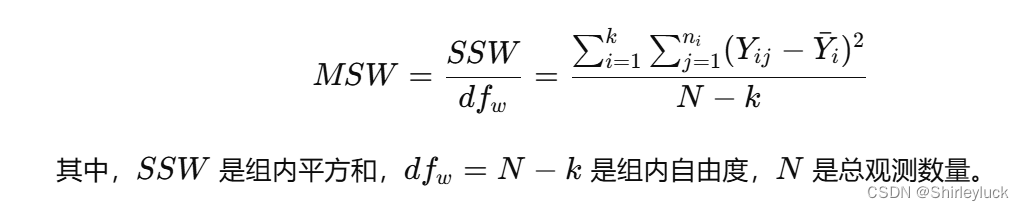
3.计算F值:

4.查找临界值:
5.做出决策:
如果计算得到的F值大于临界值,则拒绝原假设,说明组间均值存在显著差异。
如果计算得到的F值小于等于临界值,则不拒绝原假设,说明组间均值不存在显著差异。
多因素方差分析
多因素方差分析(Two-Way ANOVA 或 Factorial ANOVA)用于同时研究两个或多个因素对结果的影响,且可以考察因素间的交互作用。例如,研究不同肥料和不同灌溉方式对作物生长的联合影响。
方差分析的假设条件
- 独立性:各组别的观测值相互独立。
- 正态性:各组别的观测值服从正态分布。
- 方差齐性:各组别的方差相等。
如果数据不符合这些假设,方差分析的结果可能会失真,因此进行正态性检验可以帮助我们评估模型的适用性。
在进行正态性检验时,我们主要关注检验的 p 值。如果 p 值较大(通常大于 0.05),则表明数据符合正态分布的假设,可以继续进行方差分析。如果 p 值较小,则可能需要考虑使用非参数方法或对数据进行转换以满足模型假设。
实际应用中的考虑
在实际应用中,必须确保满足方差分析的假设条件,否则结果可能不可靠。当假设条件不满足时,可以考虑使用非参数检验(如Kruskal-Wallis检验)或调整模型(如方差不齐的情形下使用Welch's ANOVA)。
结论
方差分析是一个强大的统计工具,可以有效地检测多个组别之间的差异。然而,应用时需要谨慎,确保数据符合基本假设,并在必要时进行模型调整或采用其他统计方法。随着统计学的不断发展,方差分析的方法和应用也在不断进步,研究人员需要不断更新知识,以便在复杂的实际问题中作出准确的判断。
R语言实操-方差分析模型
方差分析(ANOVA)模型用于比较多个组之间的均值是否有显著差异。进行方差分析模型,最好对数据进行正态性检验。正态性检验有助于确认方差分析模型的假设是否满足,特别是方差分析对数据的正态性有一定的要求。写了另一篇关于正态性检验的文章:
5.22 R语言-正态性检验-CSDN博客文章浏览阅读66次,点赞2次,收藏4次。正态性检验的目的是确定一组数据是否符合正态分布(也称高斯分布)。在统计分析和数据建模中,正态性假设是许多统计方法和模型的基础。了解数据是否符合正态分布有助于选择适当的统计方法和确保分析结果的有效性。本文主要从方面来进行正态性检验。即假设检验的角度来说,数据是否服从正态分布可以通过与“”这样一个零假设进行假设检验计算,构建相关统计量来计算出检验结果。文中提及的Q-Q Plot是正态检验 (Normality Test)——常见方法汇总与简述-CSDN博客。https://blog.csdn.net/Shirleyluck/article/details/139131768?spm=1001.2014.3001.5501![]() https://blog.csdn.net/Shirleyluck/article/details/139131768?spm=1001.2014.3001.5501
https://blog.csdn.net/Shirleyluck/article/details/139131768?spm=1001.2014.3001.5501
进行方差分析(ANOVA)模型的步骤:
-
准备数据:确保你的数据是干净和适合分析的。
-
拟合模型:使用
aov函数拟合方差分析模型。 -
检验模型假设:包括正态性检验和方差齐性检验。
-
查看结果:使用
summary函数查看方差分析的结果
m = aov(Time ~ IDE, data=ide2)使用 aov 函数来拟合一个方差分析(ANOVA)模型。具体而言,你正在比较不同 IDE 组别之间的 Time 数据是否存在显著差异。
aov(Time ~ IDE, data=ide2): 这行代码指定模型的公式,即Time是因变量,IDE是自变量。data=ide2指定了数据来源。m =: 这行代码将拟合的模型赋值给变量m,以便后续进行模型检验和结果分析。
可以使用 summary(m) 来查看方差分析的结果,了解各个组别之间的差异是否显著。
summary(m) 的输出通常包含以下部分:
- Df(自由度):自变量和误差的自由度。
- Sum Sq(平方和):自变量和误差的平方和。
- Mean Sq(均方):平方和除以相应的自由度。
- F value(F值):自变量的均方除以误差的均方得到的F值。
- Pr(>F)(P值):F值对应的P值,用于判断显著性。
# 拟合方差分析模型
m <- aov(Time ~ IDE, data = ide2)# 正态性检验
install.packages("nortest")
library(nortest)
shapiro.test(ide2[ide2$IDE == "VStudio",]$Time)
shapiro.test(ide2[ide2$IDE == "Eclipse",]$Time)# 方差齐性检验
bartlett.test(Time ~ IDE, data = ide2)
install.packages("car")
library(car)
leveneTest(Time ~ IDE, data = ide2)# 查看方差分析的结果
summary(m)
绘制Q-Q 图
为了评估方差分析模型(ANOVA)假设的正态性,使用qqnorm和qqline绘制 Q-Q 图。 Q-Q 图(Quantile-Quantile Plot)是一种图形方法,用于比较数据的分布与正态分布。如果数据点大致沿着一条直线分布,则数据可以被认为是正态分布的。

##试试检验假设
#首先是正态性假设
# Shapiro-Wilk normality test(夏皮罗-威尔克检验)
shapiro.test(ide2[ide2$IDE == "VStudio",]$Time) #H0:研究对象符合正态分布。
shapiro.test(ide2[ide2$IDE == "Eclipse",]$Time)
## 满足正态性假设# 但真正重要的是残差正态性【仅展示】
m = aov(Time ~ IDE, data=ide2) # fit model
shapiro.test(residuals(m)) # test residuals
qqnorm(residuals(m)); qqline(residuals(m)) # plot residuals
## 如果残差是正态分布的,那么这些点应该近似地落在一条直线上。
## qqline函数在这图上添加了一条参考线,这条参考线是正态分布的理论分位数线,有助于直观判断残差是否近似正态分布。# 不正态可以尝试数据转换【仅展示】
ide2$logTime = log(ide2$Time) # log transform
View(ide2) # verify#其次是方差齐性假设 # 方差齐性检验就是看两总体方差是否相等.比如在两独立样本的t检验中,两总体方差1.相等 2.不相等
install.packages("car")
library(car)
leveneTest(Time ~ IDE, data=ide2, center=mean) # Levene's test:用于检验两组及两组以上独立样本的方差是否相等。
leveneTest(Time ~ IDE, data=ide2, center=median) # Brown-Forsythe test: Brown-Forsythe检验是指采用Brown-Forsythe分布的统计量进行的各组均值是否相等的检验。##执行独立样本T检验: 单总体t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。
t.test(Time ~ IDE, data=ide2, var.equal=TRUE) #var.equal= TRUE 方差相等
###根据上述结果,可以得出结论:有足够证据拒绝零假设,接受备择假设,即Eclipse和VStudio在完成任务所需平均时间上存在显著差异。
###具体来说,Eclipse组的平均时间比VStudio组多166.05个单位(468.15 - 302.10),并且这个差异是统计上显著的。
相关文章:

5.23R语言-参数假设检验
理论 方差分析(ANOVA, Analysis of Variance)是统计学中用来比较多个样本均值之间差异的一种方法。它通过将总变异分解为不同来源的变异来检测因子对响应变量的影响。方差分析广泛应用于实验设计、质量控制、医学研究等领域。 方差分析的基本模型 方差…...

rnn 和lstm源码学习笔记
目录 rnn学习笔记 lstm学习笔记 rnn学习笔记 import torchdef rnn(inputs, state, params):# inputs的形状: (时间步数量, 批次大小, 词表大小)W_xh, W_hh, b_h, W_hq, b_q paramsH stateoutputs []# 遍历每个时间步for X in inputs:# 计算隐藏状态 HH torch.tanh(torch.…...

解析Java中1000个常用类:CharSequence类,你学会了吗?
在 Java 编程中,字符串操作是最常见的任务之一。为了提供一种灵活且统一的方式来处理不同类型的字符序列,Java 引入了 CharSequence 接口。 通过实现 CharSequence 接口,各种字符序列类可以提供一致的 API,增强了代码的灵活性和可扩展性。 本文将深入探讨 CharSequence 接…...

微服务远程调用之拦截器实战
微服务远程调用之拦截器实战 前言: 在我们开发过程中,很可能是项目是从0到1开发,或者在原有基础上做二次开发,这次是根据已有代码做二次开发,需要在我们微服务一【这里方便举例,我们后面叫模版微服务】调用…...

德人合科技——天锐绿盾内网安全管理软件 | -文档透明加密模块
天锐绿盾文档加密功能能够为各种模式的电子文档提供高强度加密保护,丰富的权限控制以及灵活的应用管理,帮助企业构建更严密的立体保密体系。 PC地址: https://isite.baidu.com/site/wjz012xr/2eae091d-1b97-4276-90bc-6757c5dfedee ————…...
超融合架构下,虚拟机高可用机制如何构建?
作者:SmartX 产品部 钟锦锌 虚拟机高可用(High Availability,简称 HA)是虚拟化/超融合平台最常用、关键的功能之一,可在服务器发生故障时通过重建业务虚拟机以降低故障对业务带来的影响。因此,为了充分保障…...
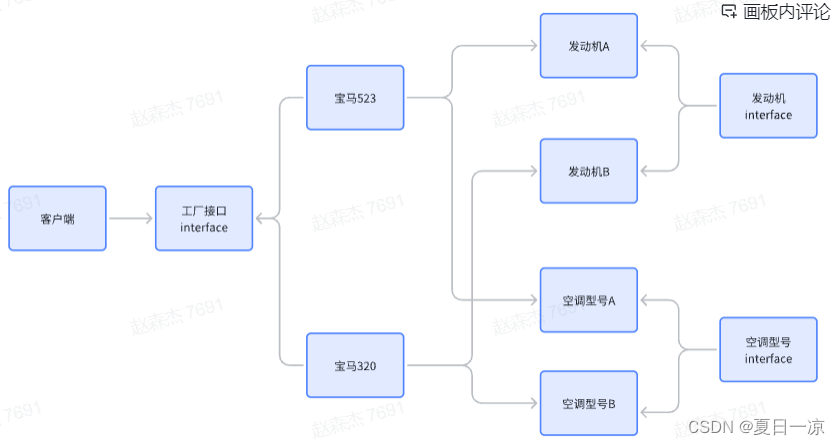
工厂模式详情
一.介绍工厂模式的用途与特点 工厂方法模式是一种创建型设计模式, 其在父类中提供一个创建对象的方法, 允许子类决定实例化对象的类型。定义工厂方法模式(Fatory Method Pattern)是指定义一个创建对象的接口,但让实现这个接口的类来决定实例…...
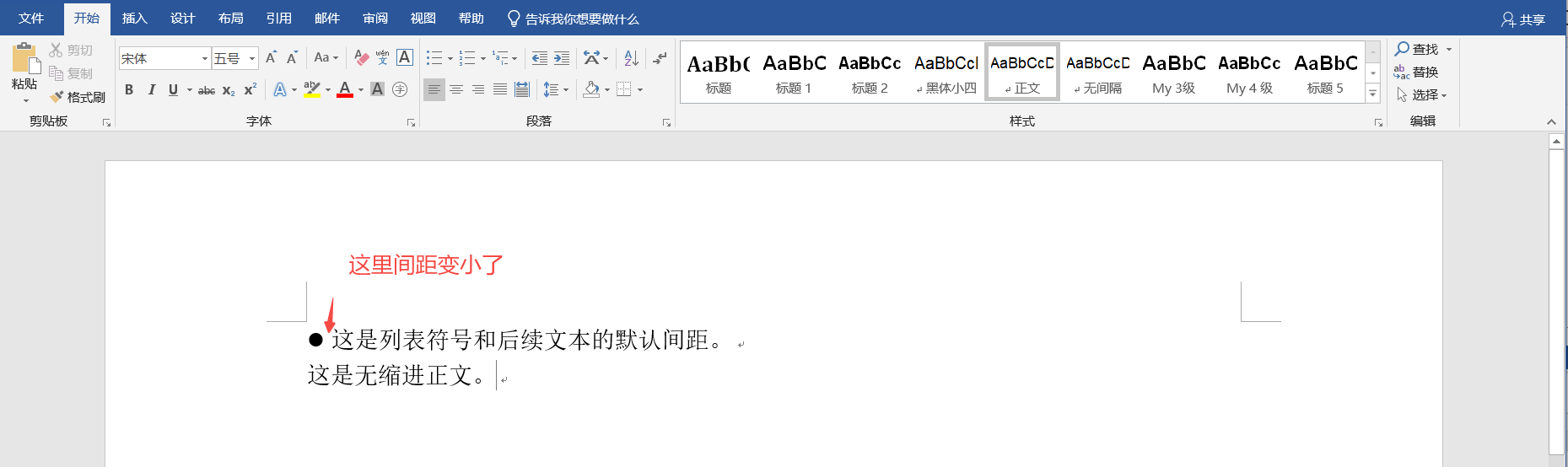
【Word】调整列表符号与后续文本的间距
1. 默认的列表格式: 2. 修改间距: ************************************************** 分割线 ************************************************************ 3. 效果...
匠心独运,B 端系统 UI 演绎华章之美
匠心独运,B 端系统 UI 演绎华章之美...
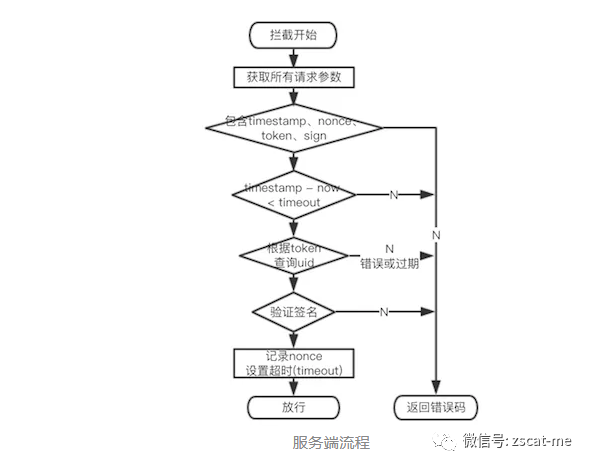
Java电商平台-开放API接口签名验证(小程序/APP)
说明:在实际的生鲜业务中,不可避免的需要对外提供api接口给外部进行调用. 这里就有一个接口安全的问题需要沟通了。下面是干货: 接口安全问题 请求身份是否合法? 请求参数是否被篡改? 请求是否唯一? AccessKey&am…...

Tale全局函数对象base
目录 1、 Tale全局函数对象base 1.1、 * tale alert删除 1.2、 * 成功弹框 1.3、 * 弹出成功,并在500毫秒后刷新页面 1.4、 * 警告弹框 1.5、 * 询问确认弹框,这里会传入then函数进来...
【启程Golang之旅】掌握Go语言数组基础概念与实际应用
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...
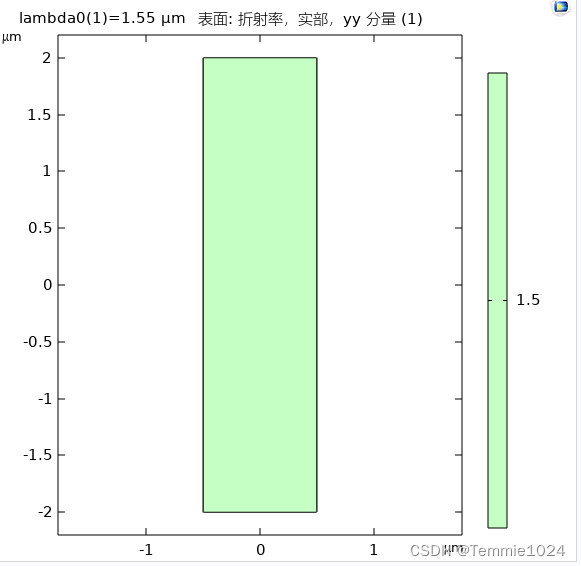
COMSOL中液晶材料光学特性模拟
前面我们根据FDTD官方文档设置了液晶指向的模型。COMSOL也可以根据相似的方法设置各项异性的周期性变化的材料。 该方法参考了luneburg_lens的COMSOL文档 在给出的文件中,可以发现定义-变量中可以使用默认坐标作为变量,即xyz。因此,折射率也可…...
虚拟现实环境下的远程教育和智能评估系统(五)
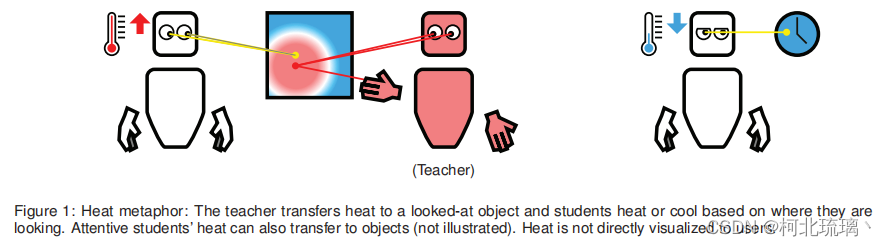
查阅相关VR眼动注意力联合教育学相关论文 1.Exploring Eye Gaze Visualization Techniques for Identifying Distracted Students in Educational VR(IEEE VR 2020) 摘要:我们提出了一种架构,使VR教学代理能够响应眼动追踪监控…...
【算法】模拟算法——Z字形变换(medium)
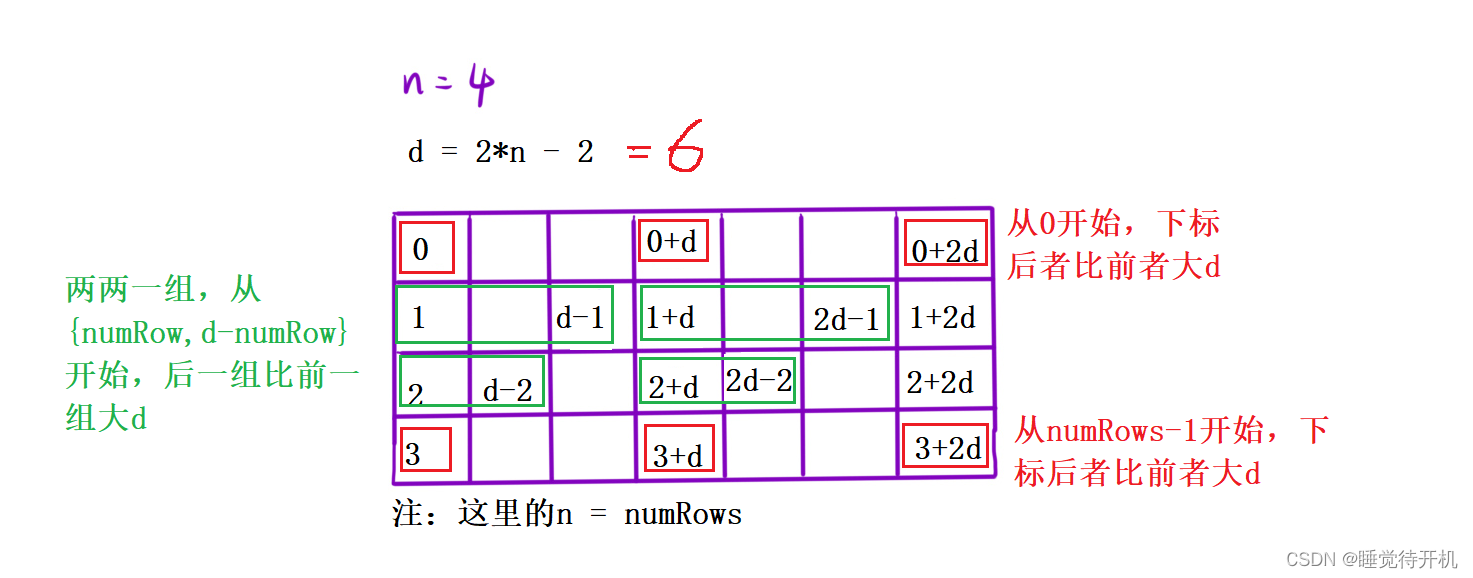
题解:模拟算法——Z字形变换(medium) 目录 1.题目2.题解3.参考代码4.总结 1.题目 题目链接:LINK 2.题解 利用模拟,来解决问题。 首先创建出一个O(numRows*n)的数组来,并按照题目要求把每个字符按顺序填进去。 这里以numRows…...
上位机图像处理和嵌入式模块部署(f103 mcu获取唯一id)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 对于stm32f103系列mcu来说,一般每一颗原厂的mcu,都会对应一个唯一的id。那这个id可以用来做什么用呢?个人认为&…...

运筹学_3.运输问题(特殊的线性规划)
目录 前言3.1 平衡运输问题中初始基可行解确定运输问题平衡运输与非平衡运输平衡运输问题的数学模型单纯形法解决平衡运输问题,初始可行基的确认 3.2 平衡运输问题的最优解判别求检验数表上作业法 3.3 产销不平衡的运输问题运输问题中产大于销的问题运输问题中产小于…...
)
科研项目书写作学习(持续更新中...)
写好一个科研项目书也是科研中很重要的一部分,所以借这篇博客做一个积累。还是以模块化的方式吧,后面慢慢那再整合逻辑。可能写的也不是很好,慢慢提升吧~ 背景 科研项目书的背景怎么写?首先要突出问题的价值(也就是做此研究的动…...

男士内裤哪个品牌好一点?2024热门男士内裤推荐
男人的内裤保质期只取决于被别人看见的次数,如果某条内裤从未被别人看见过,那它永远都是你的新内裤。也就是说,只要穿着破内裤这尴尬的瞬间没被目击,男人就能永远和一条内裤在一起。 实际上如果长时间不更换男士内裤,…...

Llama模型家族之RLAIF 基于 AI 反馈的强化学习(六) RLAIF 代码实战
LlaMA 3 系列博客 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 基于 LlaMA…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
