leetcode 115.不同的子序列
思路:LCS类dp
这道题的思考思路其实就是把以两个字符串结尾作为状态方程。
dp[i][j]的意义就是在s字符串在以s[i]结尾的字符串的情况下,所能匹配出t字符串以t[j]结尾的字符串个数。
本质上其实是一个LCS类的状态方程,只不过是意义不一样了,转移方程不一样了。
那么,我们知道了状态意义之后,我们就需要知道转移方程怎么写。
首先我们需要比较每一个字符串,以s作为匹配的主体,去匹配t。当s[i]==t[j]的时候,说明这个时候结尾处我们是可以用这意味匹配的,那么我们这一位考虑和t[j]匹配了之后,就只需要考虑后面的字符串就行了,也就是dp[i-1][j-1]。但是我们还有一种情况,比如bagg,和bag这个距离,我们除了判断除了dp[i-1][j-1]这个状态之外,需要知道dp[i-1][j]的状态,因为这里我们如果不考虑s[i]的匹配了(选与不选的问题),那么上一位我们就需要考虑是不是和当前t的这一位匹不匹配。
之后,就是s[i]!=t[j]的情况,这里就简单了,因为无论如何s[i]都不能满足t[j]的匹配,我们只需要考虑上一位的匹配情况就可以了。
注意:初始化的时候我们需要额外注意,在t为空的时候,我们无论怎么匹配就只有一种情况,也就是dp[i][0]=1,因为只有一个空集能够匹配;当s为空的时候,其实就没有什么匹配情况了,本身需要匹配的字符串都没有,也就没有什么个数方案了,也就是dp[0][i]=0。
当然,当s,t都是空的时候,也就是一种方案,都是匹配空集。
还有,在递推的过程中,其实dp可能会暴int,所以需要及时在中途进行类型变化并取余。
class Solution {
public:int numDistinct(string s, string t) {vector<vector<int>>dp(s.size()+1,vector<int>(t.size()+1,0));for(int i=1;i<=s.size();i++){dp[i][0]=1;}for(int i=1;i<=t.size();i++){dp[0][i]=0;}dp[0][0]=1;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]){dp[i][j]=(long)(dp[i-1][j-1]+dp[i-1][j])%1000000007;}else{dp[i][j]=(long)dp[i-1][j]%1000000007;}}}return dp[s.size()][t.size()];}
};相关文章:

leetcode 115.不同的子序列
思路:LCS类dp 这道题的思考思路其实就是把以两个字符串结尾作为状态方程。 dp[i][j]的意义就是在s字符串在以s[i]结尾的字符串的情况下,所能匹配出t字符串以t[j]结尾的字符串个数。 本质上其实是一个LCS类的状态方程,只不过是意义不一样了…...

二叉树的顺序实现-堆
一、什么是堆 在数据结构中,堆(Heap)是一种特殊的树形数据结构,用数组存储,通常被用来实现优先队列。 堆具有以下特点: 堆是一棵完全二叉树(Complete Binary Tree),即…...

【Maven】Maven主要知识点目录整理
1. Maven的基本概念 作者相关文章链接: 1、【Maven】简介_下载安装-CSDN博客 定义:Maven是Apache的一个开源项目,是Java开发环境中用于管理和构建项目,以及维护依赖关系的强大软件项目管理工具。作用:简化了项目依赖…...
Coolmuster Android Assistant: 手机数据管理的全能助手
在数字化时代,智能手机不仅是通讯工具,更是个人数据的中心。随着数据量的不断增加,如何有效管理和保护这些数据成为了一个重要议题。Coolmuster Android Assistant应运而生,它是一款专为安卓用户设计的综合数据管理软件࿰…...

03-树3 Tree Traversals Again(浙大数据结构PTA习题)
03-树3 Tree Traversals Again 分数 25 作者 陈越 An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, th…...

Java项目对接redis,客户端是选Redisson、Lettuce还是Jedis?
JAVA项目对接redis,客户端是选Redisson、Lettuce还是Jedis? 一、客户端简介1. Jedis介绍2. Lettuce介绍3. Redisson介绍 二、横向对比三、选型说明 在实际的项目开发中,对于一个需要对接Redis的项目来说,就面临着选择合适的Redis客…...

AngularJS Web前端框架:深入探索与应用实践
AngularJS Web前端框架:深入探索与应用实践 AngularJS,作为一款强大的Web前端框架,为开发者提供了丰富的功能和工具,使得构建复杂且交互性强的Web应用变得更为便捷。本文将从四个方面、五个方面、六个方面和七个方面对AngularJS进…...

SQL 入门:使用 MySQL 进行数据库操作
SQL 入门:使用 MySQL 进行数据库操作 目录 引言SQL 基础 SQL 语言概述MySQL 简介 数据库设计基础 数据库与表的设计常见数据类型 MySQL 安装与配置 安装 MySQL基本配置与连接 基本 SQL 语句 数据库的创建与删除表的创建、修改与删除数据插入、更新与删除 数据查询…...
window安装ffmpeg播放本地摄像头视频
1、安装ffmpeg ffmpeg官方网站:FFmpeg 下载后解压文件夹名为ffmpeg 2、设置环境变量 目录 1、安装ffmpeg 设置环境变量 以F:\software\after\ffmpeg\bin为例 在命令行中输入ffmpeg出现下方代表安装成功 3、通过ffmpeg播放本地电脑摄像头 鼠标右击开始按钮&…...

【嵌入式DIY实例】-OLED显示网络时钟
OLED显示网络时钟 文章目录 OLED显示网络时钟1、硬件准备与接线2、代码实现在上一个ESP8266 NodeMCU文章中,我们用DS3231 RTC芯片和SSD1306 OLED制作了一个简单的实时时钟,时间和日期显示在SSD1306屏幕上,并且可以通过两个按钮进行设置。 在本中,我们将使用ESP 8266 NodeMC…...

【线程相关知识】
今日内容概要 开启线程的两种方式TCP服务端实现并发效果线程对象的join方法线程间数据共享线程对象属性及其他方法守护线程线程互斥锁GIL全局解释器锁多进程与多线程的实际应用场景 今日内容详细 开启线程的两种方式 # import time # from multiprocessing import Process #…...

鸿蒙ArkTS声明式开发:跨平台支持列表【透明度设置】 通用属性
透明度设置 设置组件的透明度。 说明: 开发前请熟悉鸿蒙开发指导文档: gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版…...

【SQL学习进阶】从入门到高级应用(九)
文章目录 子查询什么是子查询where后面使用子查询from后面使用子查询select后面使用子查询exists、not existsin和exists区别 union&union alllimit 🌈你好呀!我是 山顶风景独好 💕欢迎来到我的博客,很高兴能够在这里和您见面…...

Web前端三大主流框架技术分享
在当今快速发展的互联网时代,Web前端技术作为连接用户与服务的桥梁,其重要性不言而喻。随着技术的不断进步,为了提升开发效率、优化用户体验,一系列强大的前端框架应运而生。其中,Angular、React和Vue.js作为当前最为主…...

dockers安装mysql
1.dockerhub上搜索自己需要安装得镜像版本 dockerhub网址:https://hub-stage.docker.com docker pull mysql:5.7 #下载自己需要得版本2.启动容器实例,并且挂载容器数据卷 docker run -d -p 3306:3306 --privilegedtrue \ -v /home/mysql/log:/var/log/…...

100道面试必会算法-27-美团2024面试第一题-前缀和矩阵
100道面试必会算法-27-美团2024面试第一题-前缀和矩阵 问题解读 给定一个 n x n 的二进制矩阵,每个元素是 0 或 1。我们的任务是计算矩阵中所有边长为 k 的子矩阵中,包含特定数量 1 的情况。例如,我们希望找到所有边长为 k 的子矩阵中包含 k…...

从摇一摇到弹窗,AD无处不在?为了不再受打扰,推荐几款好用的屏蔽软件,让手机电脑更清爽
当我们沉浸在智能手机带来的便捷与乐趣中时,内置AD如同不速之客,时常打断我们的体验。 尤其是手机上那些“摇一摇”跳转,稍有不慎就会跳转到其他应用,令人不胜其烦。同样,电脑上的内置AD也如影随形,影响了我…...
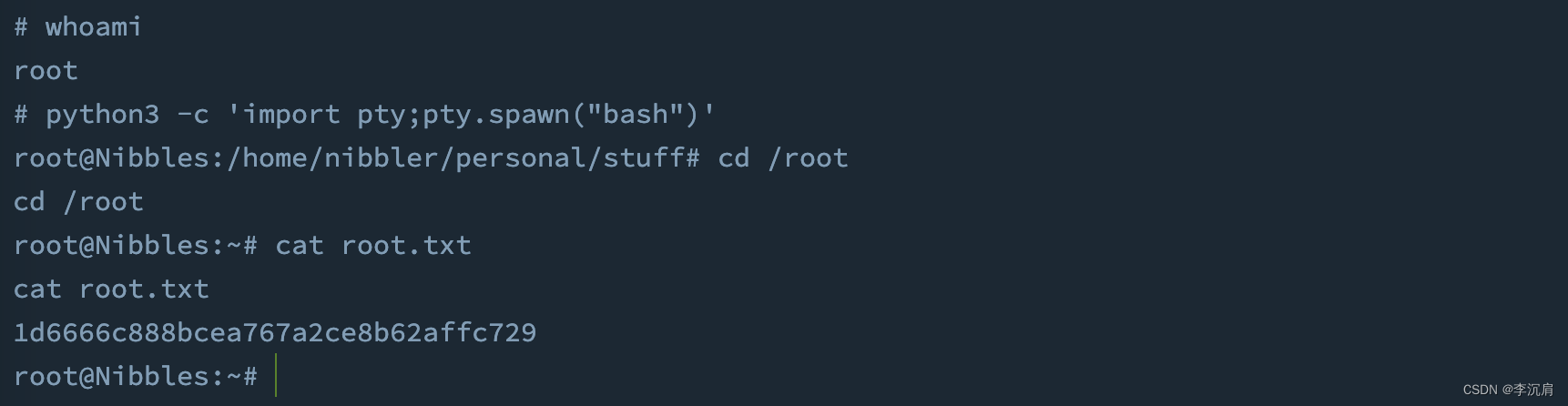
HackTheBox-Machines--Nibbles
Nibbles 测试过程 1 信息收集 NMAP 80 端口 网站出了打印出“Hello world!”外,无其他可利用信息,但是查看网页源代码时,发现存在一个 /nibbleblog 文件夹 检查了 http://10.129.140.63/nibbleblog/ ,发现了 /index.p…...

东方博宜1703 - 小明买水果
问题描述 小明去超市买了若干斤水果,你能根据水果的单价,小明买的水果数量,编一个程序计算出总金额,并打印出清单。 输入 输入两个值, 第一个为商品的单价,是一个小数。 第二个为商品的数量,…...
mac电脑用谷歌浏览器对安卓手机H5页面进行inspect
1、mac上在谷歌浏览器上输入 chrome://inspect 并打开该页面。 2、连接安卓手机到Mac电脑:使用USB数据线将安卓手机连接到Mac电脑。 3、手机上打开要的h5页面 Webview下面选择要的页面,点击inspect,就能像谷歌浏览器页面打开下面的页面&#…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
