100道面试必会算法-27-美团2024面试第一题-前缀和矩阵
100道面试必会算法-27-美团2024面试第一题-前缀和矩阵

问题解读
给定一个 n x n 的二进制矩阵,每个元素是 0 或 1。我们的任务是计算矩阵中所有边长为 k 的子矩阵中,包含特定数量 1 的情况。例如,我们希望找到所有边长为 k 的子矩阵中包含 k*k/2 个 1 的子矩阵数量。
输入格式:
第一行:一个整数 n,表示矩阵的大小。
接下来的 n 行:每行包含一个长度为 n 的二进制字符串,表示矩阵中的一行。
输出格式:
对于每个可能的子矩阵边长 k,输出一个整数,表示边长为 k 且包含特定数量 1 的子矩阵的数量。如果 k 是奇数
计算一个大小为 n x n 的矩阵中,所有边长为 k 的子矩阵中包含特定数量的 1 的情况。通过三个主要步骤来解决这个问题:
- 读取输入并初始化矩阵:读取一个
n x n的矩阵,并构建前缀和矩阵m和sum。 - 计算前缀和:通过构建前缀和矩阵,可以快速计算任何子矩阵的元素和。
- 检查子矩阵:对于每个可能的子矩阵,检查其是否满足条件。
什么是前缀和矩阵
前缀和矩阵是一种用于快速计算二维数组(矩阵)中子矩阵元素之和的数据结构。通过预先计算和存储每个位置的前缀和,我们可以在常数时间内计算任意子矩阵的元素和。
前缀和矩阵的构建
给定一个大小为 n x n 的矩阵 nums,我们可以构建一个前缀和矩阵 m。前缀和矩阵的每个元素 m[i][j] 表示从矩阵的左上角 (1,1) 到位置 (i,j) 的所有元素的和。其递推公式为:
m[i][j]=m[i−1][j]+m[i][j−1]−m[i−1][j−1]+nums[i][j]
在边界条件下:
m[i][0]和m[0][j]初始为 0,因为这些位置不可能有左上方的矩阵。
解决方案
我们将通过以下步骤来解决这个问题:
- 读取输入并初始化矩阵:我们将读取输入的矩阵,并使用两个矩阵
nums和m来存储矩阵元素和前缀和。 - 计算前缀和:前缀和矩阵
m可以帮助我们快速计算任何子矩阵的元素和。前缀和矩阵的计算公式为:m[i][j]=m[i−1][j]+m[i][j−1]−m[i−1][j−1]+nums[i][j] - 检查子矩阵:对于每个可能的子矩阵,我们通过前缀和矩阵快速计算其元素和,并检查其是否满足条件。
代码实现
import java.util.Scanner;public class Meituan {public static void main(String[] args) {Scanner input = new Scanner(System.in);int n = input.nextInt();char[] chars;int[][] m = new int[n + 1][n + 1];int[][] nums = new int[n + 1][n + 1];// 初始化矩阵和前缀和矩阵for (int i = 1; i <= n; i++) {chars = input.next().toCharArray();for (int j = 1; j <= n; j++) {nums[i][j] = chars[j - 1] - '0';m[i][j] = m[i - 1][j] + m[i][j - 1] - m[i - 1][j - 1] + nums[i][j];}}// 遍历每个可能的子矩阵边长 kfor (int k = 1; k <= n; k++) {if (k % 2 != 0) {System.out.println(0);continue;}int ans = 0;// 遍历每个可能的子矩阵for (int i = 1; i + k - 1 <= n; i++) {for (int j = 1; j + k - 1 <= n; j++) {int x = i + k - 1;int y = j + k - 1;int sum = m[x][y] - m[i - 1][y] - m[x][j - 1] + m[i - 1][j - 1];if (sum == k * k / 2) ans++;}}System.out.println(ans);}}
}代码解析
- 初始化矩阵和前缀和矩阵:
nums用于存储输入的二进制矩阵。m用于存储前缀和矩阵,通过累加计算得到。
- 计算前缀和:
- 前缀和矩阵
m[i][j]通过公式m[i][j] = m[i-1][j] + m[i][j-1] - m[i-1][j-1] + nums[i][j]计算得到。 - 这样可以在常数时间内计算任何子矩阵的元素和。
- 前缀和矩阵
- 遍历子矩阵:
- 对于每个可能的子矩阵,计算其元素和
sum。 - 检查该和是否等于
k*k/2,如果是,则计数器ans增加。
- 对于每个可能的子矩阵,计算其元素和
总结
任何子矩阵的元素和。
3. 遍历子矩阵:
- 对于每个可能的子矩阵,计算其元素和
sum。 - 检查该和是否等于
k*k/2,如果是,则计数器ans增加。
总结
通过使用前缀和矩阵,可以高效地计算出所有边长为 k 的子矩阵中包含特定数量 1 的情况。这种方法大大减少了时间复杂度,能够在合理的时间内解决较大的输入规模。
相关文章:

100道面试必会算法-27-美团2024面试第一题-前缀和矩阵
100道面试必会算法-27-美团2024面试第一题-前缀和矩阵 问题解读 给定一个 n x n 的二进制矩阵,每个元素是 0 或 1。我们的任务是计算矩阵中所有边长为 k 的子矩阵中,包含特定数量 1 的情况。例如,我们希望找到所有边长为 k 的子矩阵中包含 k…...

从摇一摇到弹窗,AD无处不在?为了不再受打扰,推荐几款好用的屏蔽软件,让手机电脑更清爽
当我们沉浸在智能手机带来的便捷与乐趣中时,内置AD如同不速之客,时常打断我们的体验。 尤其是手机上那些“摇一摇”跳转,稍有不慎就会跳转到其他应用,令人不胜其烦。同样,电脑上的内置AD也如影随形,影响了我…...
HackTheBox-Machines--Nibbles
Nibbles 测试过程 1 信息收集 NMAP 80 端口 网站出了打印出“Hello world!”外,无其他可利用信息,但是查看网页源代码时,发现存在一个 /nibbleblog 文件夹 检查了 http://10.129.140.63/nibbleblog/ ,发现了 /index.p…...

东方博宜1703 - 小明买水果
问题描述 小明去超市买了若干斤水果,你能根据水果的单价,小明买的水果数量,编一个程序计算出总金额,并打印出清单。 输入 输入两个值, 第一个为商品的单价,是一个小数。 第二个为商品的数量,…...
mac电脑用谷歌浏览器对安卓手机H5页面进行inspect
1、mac上在谷歌浏览器上输入 chrome://inspect 并打开该页面。 2、连接安卓手机到Mac电脑:使用USB数据线将安卓手机连接到Mac电脑。 3、手机上打开要的h5页面 Webview下面选择要的页面,点击inspect,就能像谷歌浏览器页面打开下面的页面&#…...
代码实践-深度学习基础-01基础函数的使用)
动手学深度学习(Pytorch版)代码实践-深度学习基础-01基础函数的使用
01基础函数的使用 主要内容 张量操作:创建和操作张量,包括重塑、填充、逐元素操作等。数据处理:使用pandas加载和处理数据,包括处理缺失值和进行one-hot编码。线性代数:包括矩阵运算、求和、均值、点积和各种范数计算…...

vm-bhyve:bhyve虚拟机的管理系统@FreeBSD
先说情况,当前创建虚拟机后网络没有调通....不明白是最近自己点背,还是确实有难度... 缘起: 前段时间学习bhyve虚拟机,发现bvm这个虚拟机管理系统,但是实践下来发现网络方面好像有问题,至少我花了两天时间…...
【Java】刚刚!突然!紧急通知!垃圾回收!
【Java】刚刚!突然!紧急通知!垃圾回收! 文章目录 【Java】刚刚!突然!紧急通知!垃圾回收!从C语言的内存管理引入:手动回收Java的垃圾回收机制引用计数器循环引用问题 可达…...
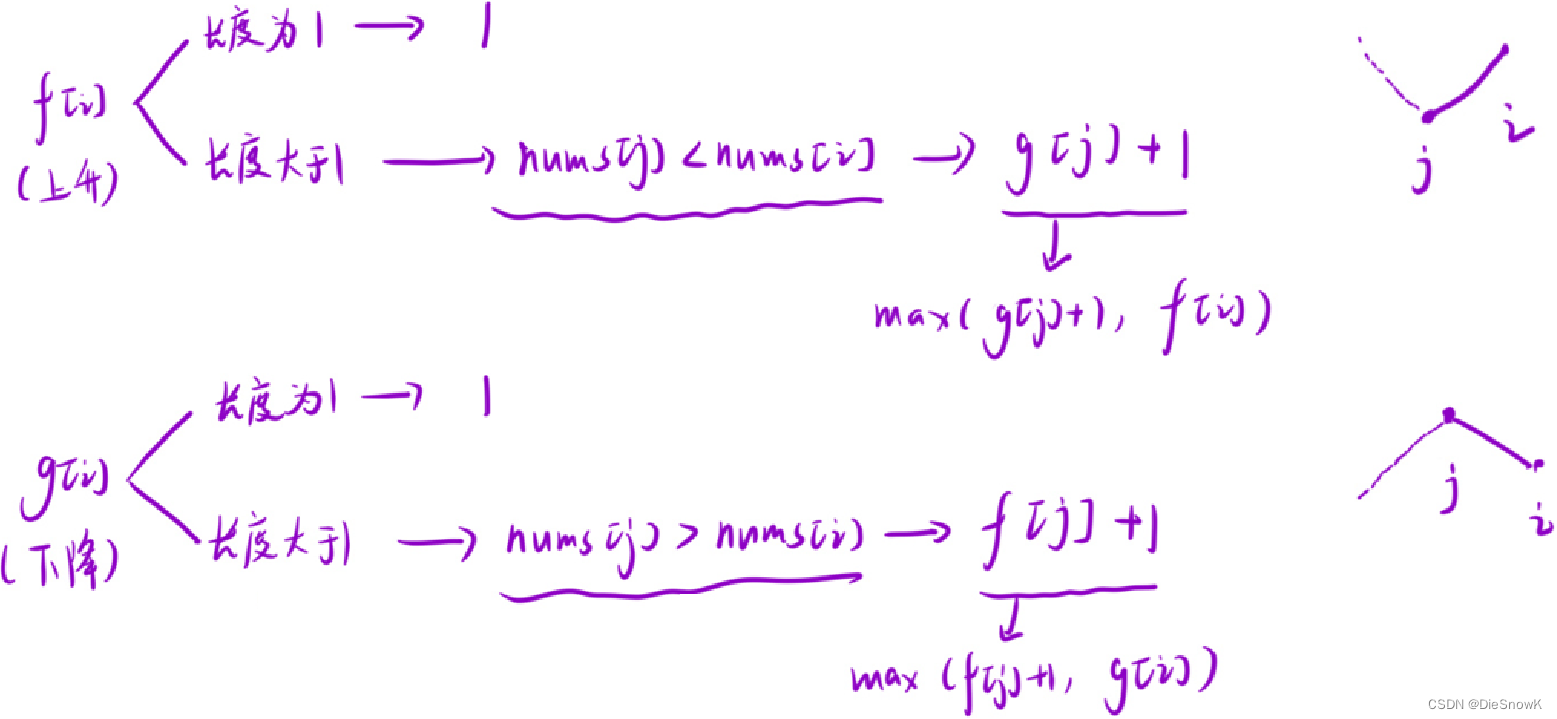
[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解
目录 0.子序列 vs 子数组1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.摆动序列1.题目链接2.题目链接3.代码实现 0.子序列 vs 子数组 子序列: 相对顺序是跟源字符串/数组是一致的但是元素和元素之间,在源字符串/数组中可以是不连续的一般时间…...

【稳定检索】2024年心理学与现代化教育、媒体国际会议(PMEM 2024)
2024年心理学与现代化教育、媒体国际会议 2024 International Conference on Psychology and Modern Education and Media 【1】会议简介 2024年心理学与现代化教育、媒体国际会议即将召开,这是一场汇聚全球心理学、教育及媒体领域精英的学术盛宴。 本次会议将深入探…...
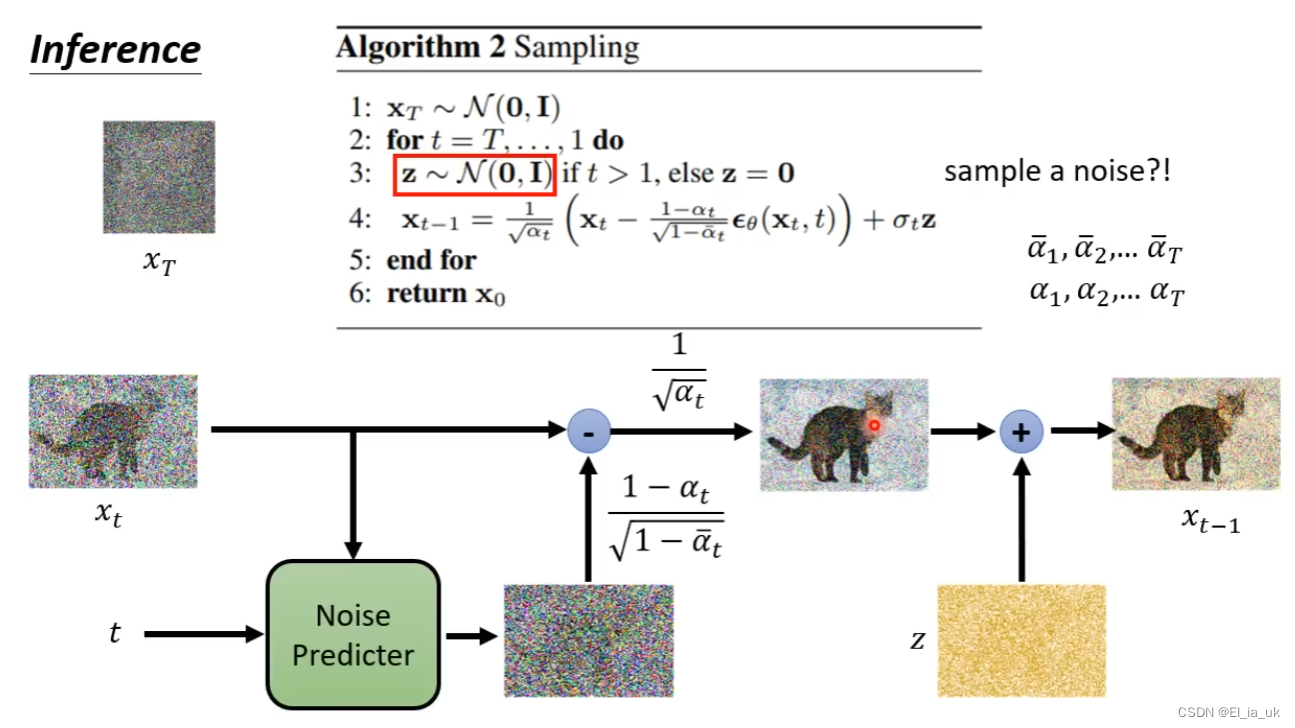
深入了解diffusion model
diffusion model是如何运作的 会输入当时noise的严重程度,根据我们的输入来确定在第几个step,并做出不同的回应。 Denoise模组内部实际做的事情 产生一张图片和产生noise难度是不一样的,若denoise 模块产生一只带噪声的猫说明这个模块已经会…...
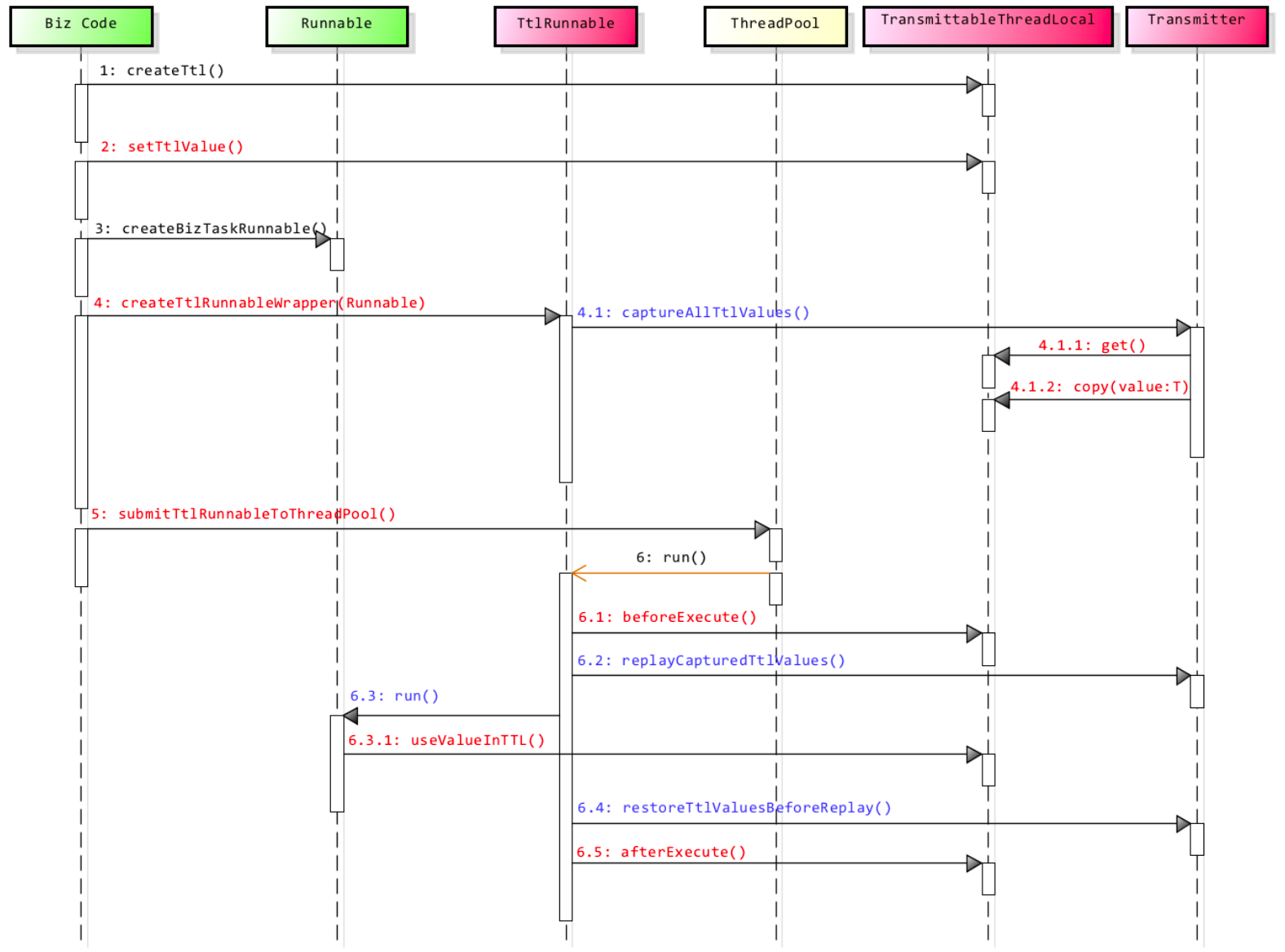
TransmittableThreadLocal原理
1、原理 TransmittableThreadLocal(简称TTL)是阿里巴巴开源的一个Java库,用于解决线程池中线程本地变量传递的问题。其底层原理主要是基于Java的ThreadLocal机制并对其进行扩展,以支持在父子线程间以及线程池中任务切换时&#x…...

华为昇腾310B初体验,OrangePi AIpro开发板使用测评
0、写在前面 很高兴收到官方的OrangePi AIpro开发板测试邀请,在过去的几年中,我在自己的博客写了一系列有关搭载嵌入式Linux系统的SBC(单板计算机)的博文,包括树莓派4系列、2K1000龙芯教育派、Radxa Rock5B、BeagleBo…...

GPTQ 量化大模型
GPTQ 量化大模型 GPTQ 算法 GPTQ 算法由 Frantar 等人 (2023) 提出,它从 OBQ 方法中汲取灵感,但进行了重大改进,可以将其扩展到(非常)大型的语言模型。 步骤 1:任意顺序量化 OBQ 方法选择权重按特定顺序…...

【GD32】05 - PWM 脉冲宽度调制
PWM PWM (Pulse Width Modulation) 是一种模拟信号电平的方法,它通过使用数字信号(通常是方波)来近似地表示模拟信号。在PWM中,信号的占空比(即高电平时间占整个周期的比例)被用来控制平均输出电压或电流。…...

JVM思维导图
帮助我们快速整理和总结JVM相关知识,有结构化认识和整体的思维模型 JVM相关详细知识和面试题...

Ollama+OpenWebUI+Phi3本地大模型入门
文章目录 Ollama+OpenWebUI+Phi3本地大模型入门一、基础环境二、Ollama三、OpenWebUI + Phi3Ollama+OpenWebUI+Phi3本地大模型入门 完全不懂大模型的请绕道,相信我李一舟的课程比较适合 Ollama提供大模型运行环境,OpenWebUI提供UI,Phi3就是那个大模型。 当然,Ollama支持超级…...
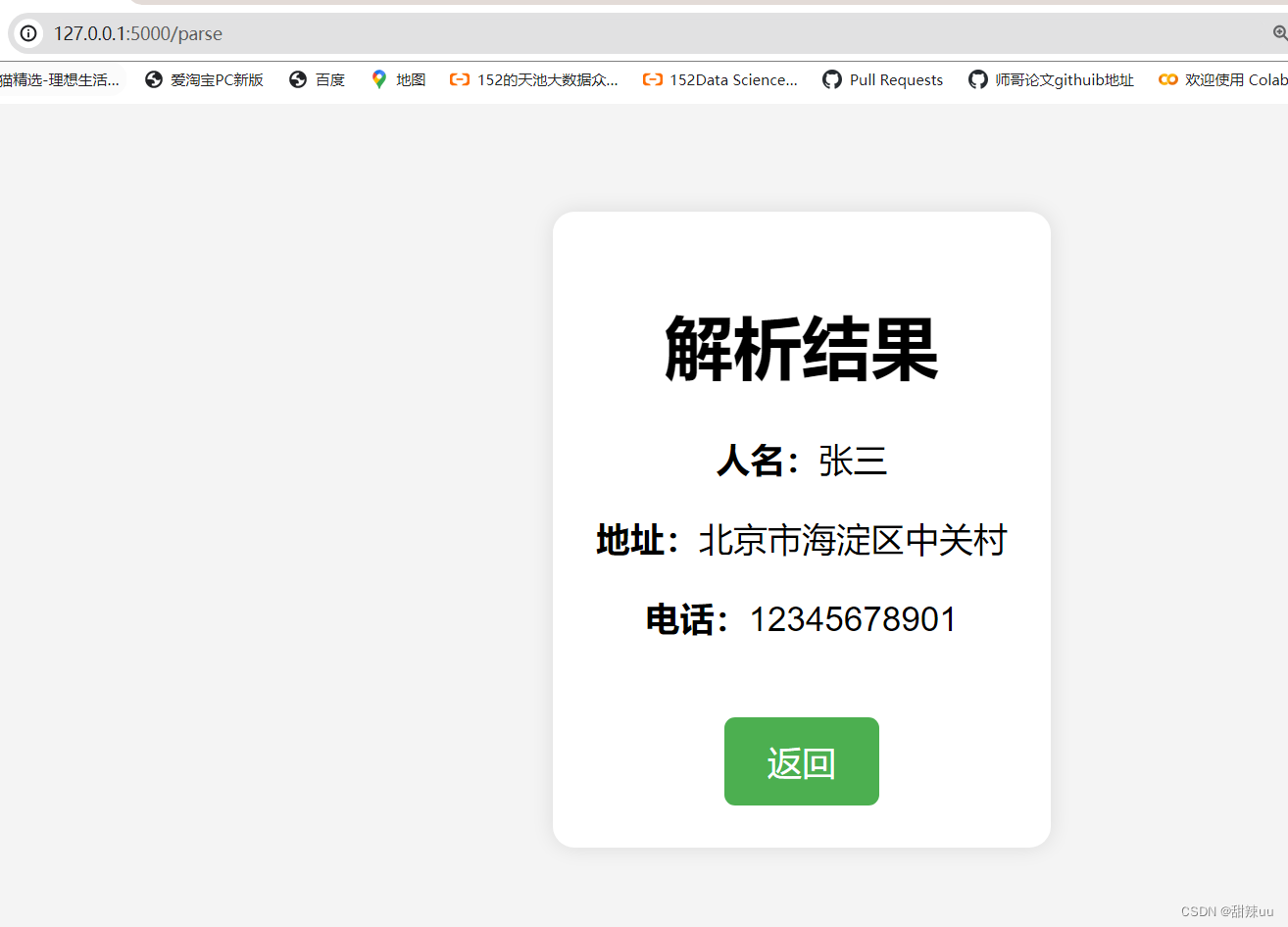
实战15:bert 命名实体识别、地址解析、人名电话地址抽取系统-完整代码数据
直接看项目视频演示: bert 命名实体识别、关系抽取、人物抽取、地址解析、人名电话地址提取系统-完整代码数据_哔哩哔哩_bilibili 项目演示: 代码: import re from transformers import BertTokenizer, BertForTokenClassification, pipeline import os import torch im…...

js 表格添加|删除一行交互
一、需求 二、实现 <div style"margin-bottom: 55px"><form action"" method"post" enctype"multipart/form-data" id"reportForm" name"sjf" style"margin-left: 25px;margin-bottom: 50px;&quo…...

如何选择合适的服务器硬件和配置?
业务需求 了解您的业务需求和负载。这将帮助您确定需要哪种类型的服务器(如文件服务器、数据库服务器、Web服务器等)以及所需的处理能力、内存、存储和网络性能。...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
