[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解
目录
- 0.子序列 vs 子数组
- 1.最长递增子序列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.摆动序列
- 1.题目链接
- 2.题目链接
- 3.代码实现
0.子序列 vs 子数组
- 子序列:
- 相对顺序是跟源字符串/数组是一致的
- 但是元素和元素之间,在源字符串/数组中可以是不连续的
- 一般时间复杂度: O ( 2 n ) O(2^n) O(2n)
- 子数组:
- 在源字符串/数组中挑出来,必须是连续的
- 子串与子数组是一个意思
- 一般时间复杂度: O ( N 2 ) O(N^2) O(N2)
- 在源字符串/数组中挑出来,必须是连续的
- 子序列其实相当于包含了子数组
- 子序列问题经典解法:两层循环
1.最长递增子序列
1.题目链接
- 最长递增子序列
2.算法原理详解
- 注意:本题思考方式非常有标志性
- 思路:
-
确定状态表示 ->
dp[i]的含义- 以
i位置元素为结尾的所有子序列中,最长递增子序列的长度
- 以
-
推导状态转移方程
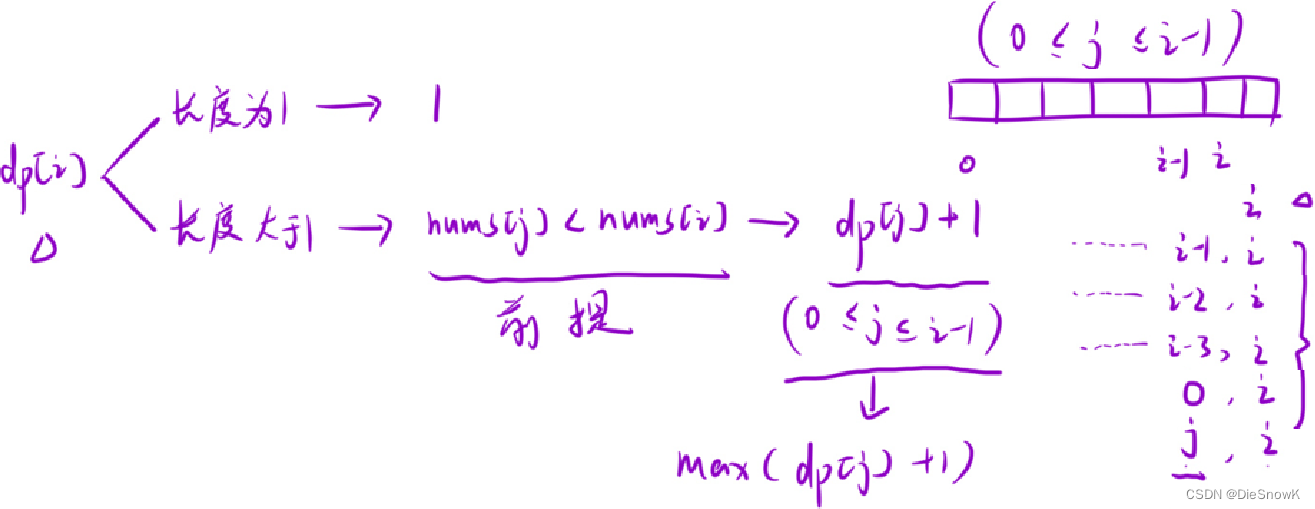
-
初始化:
vector<int> dp(n, 1) -
确定填表顺序:从左往右
-
确定返回值:整个
dp表里的最大值
-
3.代码实现
int lengthOfLIS(vector<int>& nums)
{int n = nums.size();vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;
}
2.摆动序列
1.题目链接
- 摆动序列
2.题目链接
- 思路:
-
确定状态表示 ->
dp[i]的含义- 以
i位置元素为结尾的所有子序列中,最长的摆动序列的长度 - 本题状态标识还可以继续划分
f[i]:以i位置元素为结尾的所有子序列中,最后一个位置呈现“上升”趋势的最长的摆动序列的长度g[i]:以i位置元素为结尾的所有子序列中,最后一个位置呈现“下降”趋势的最长的摆动序列的长度
- 以
-
推导状态转移方程
- 令
j为i前面的任一一个数
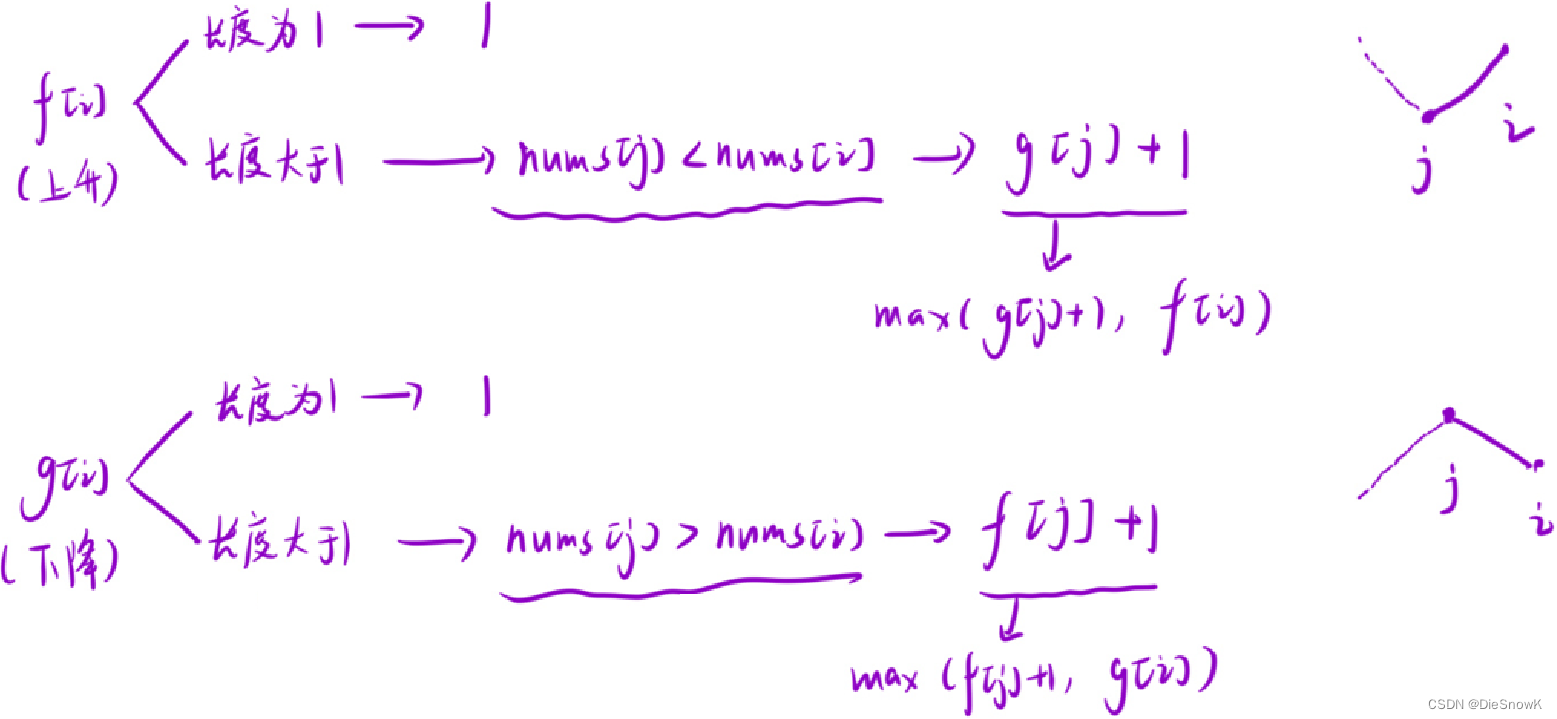
- 令
-
初始化:
vector<int> f(n, 1), g(n, 1) -
确定填表顺序:从左往右,两个表一起填
-
确定返回值:两个
dp表里的最大值
-
3.代码实现
int wiggleMaxLength(vector<int>& nums)
{int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){f[i] = max(f[i], g[j] + 1);}else if(nums[j] > nums[i]){g[i] = max(g[i], f[j] + 1);}}ret = max(ret, max(f[i], g[i]));}return ret;
}
相关文章:

[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解
目录 0.子序列 vs 子数组1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.摆动序列1.题目链接2.题目链接3.代码实现 0.子序列 vs 子数组 子序列: 相对顺序是跟源字符串/数组是一致的但是元素和元素之间,在源字符串/数组中可以是不连续的一般时间…...

【稳定检索】2024年心理学与现代化教育、媒体国际会议(PMEM 2024)
2024年心理学与现代化教育、媒体国际会议 2024 International Conference on Psychology and Modern Education and Media 【1】会议简介 2024年心理学与现代化教育、媒体国际会议即将召开,这是一场汇聚全球心理学、教育及媒体领域精英的学术盛宴。 本次会议将深入探…...
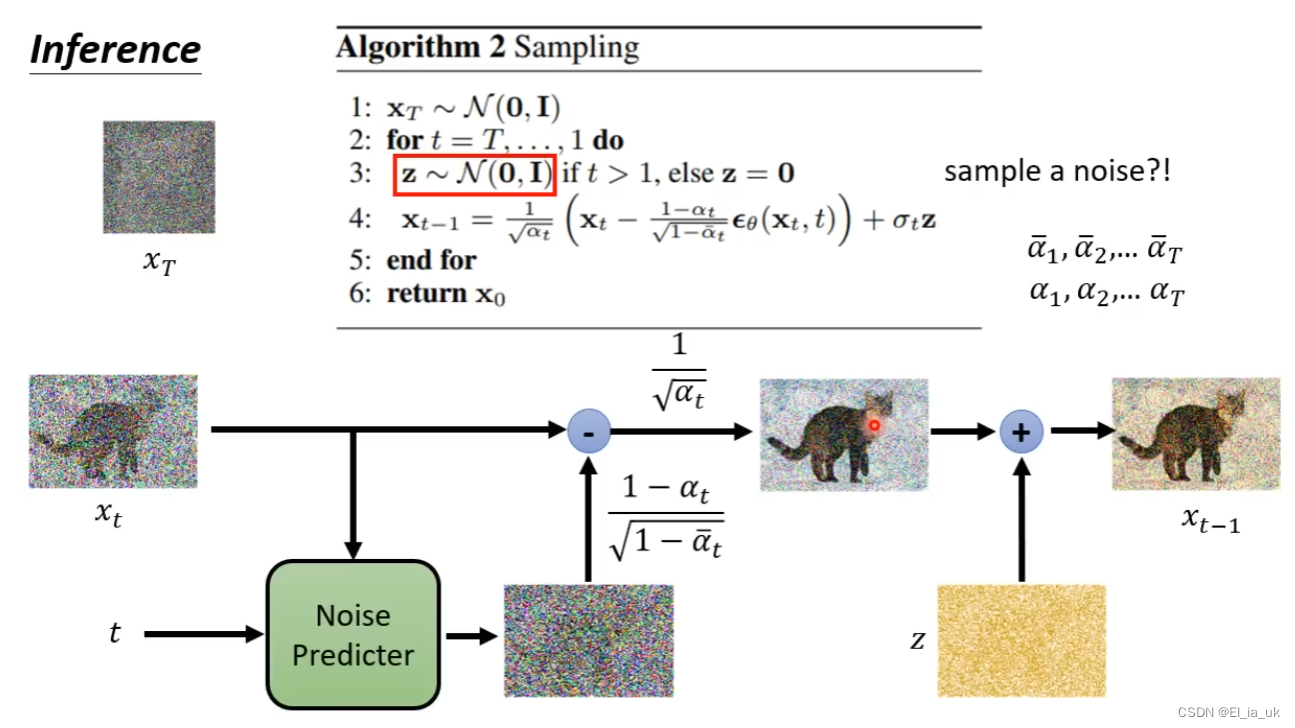
深入了解diffusion model
diffusion model是如何运作的 会输入当时noise的严重程度,根据我们的输入来确定在第几个step,并做出不同的回应。 Denoise模组内部实际做的事情 产生一张图片和产生noise难度是不一样的,若denoise 模块产生一只带噪声的猫说明这个模块已经会…...
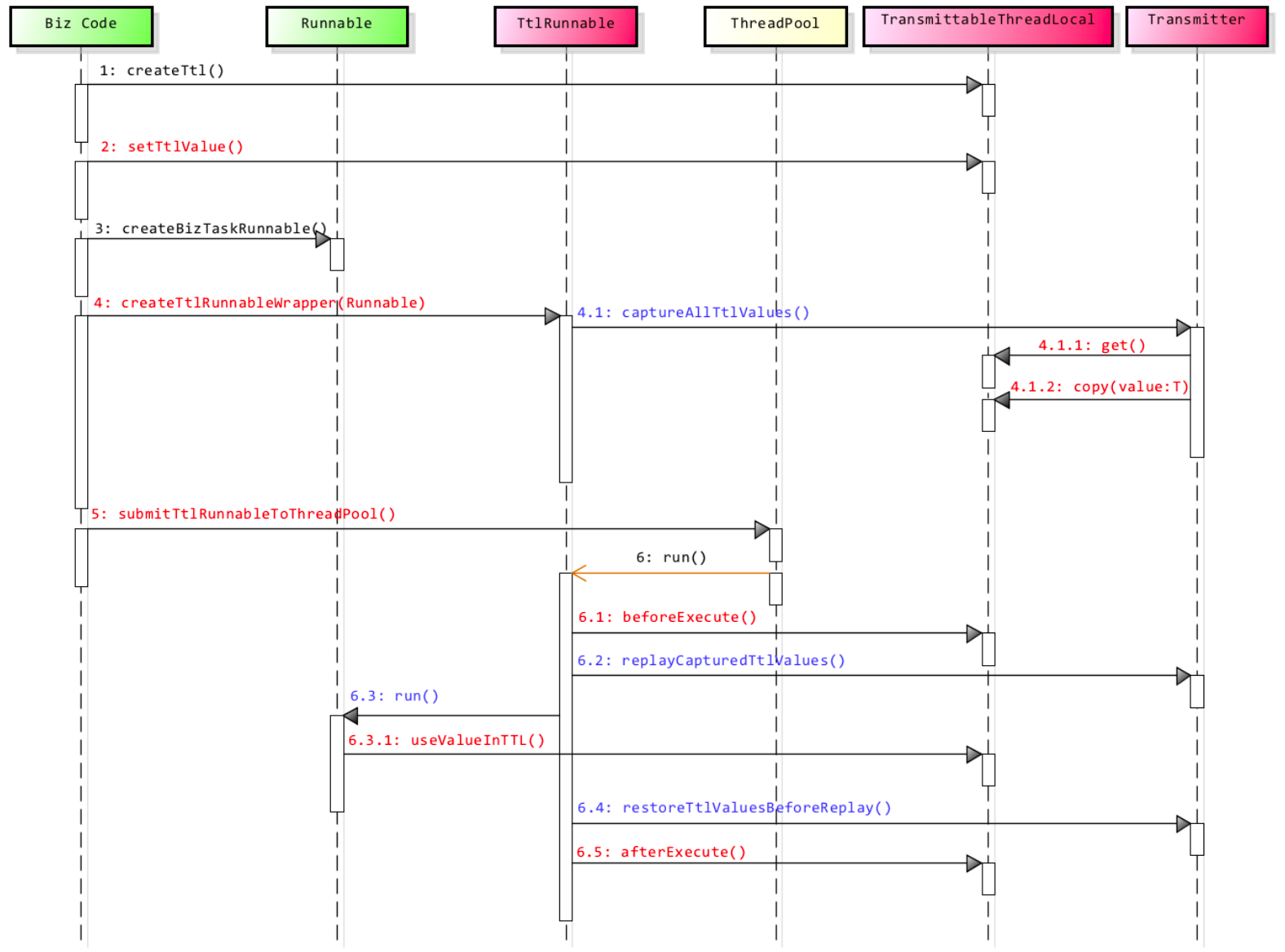
TransmittableThreadLocal原理
1、原理 TransmittableThreadLocal(简称TTL)是阿里巴巴开源的一个Java库,用于解决线程池中线程本地变量传递的问题。其底层原理主要是基于Java的ThreadLocal机制并对其进行扩展,以支持在父子线程间以及线程池中任务切换时&#x…...

华为昇腾310B初体验,OrangePi AIpro开发板使用测评
0、写在前面 很高兴收到官方的OrangePi AIpro开发板测试邀请,在过去的几年中,我在自己的博客写了一系列有关搭载嵌入式Linux系统的SBC(单板计算机)的博文,包括树莓派4系列、2K1000龙芯教育派、Radxa Rock5B、BeagleBo…...

GPTQ 量化大模型
GPTQ 量化大模型 GPTQ 算法 GPTQ 算法由 Frantar 等人 (2023) 提出,它从 OBQ 方法中汲取灵感,但进行了重大改进,可以将其扩展到(非常)大型的语言模型。 步骤 1:任意顺序量化 OBQ 方法选择权重按特定顺序…...

【GD32】05 - PWM 脉冲宽度调制
PWM PWM (Pulse Width Modulation) 是一种模拟信号电平的方法,它通过使用数字信号(通常是方波)来近似地表示模拟信号。在PWM中,信号的占空比(即高电平时间占整个周期的比例)被用来控制平均输出电压或电流。…...

JVM思维导图
帮助我们快速整理和总结JVM相关知识,有结构化认识和整体的思维模型 JVM相关详细知识和面试题...

Ollama+OpenWebUI+Phi3本地大模型入门
文章目录 Ollama+OpenWebUI+Phi3本地大模型入门一、基础环境二、Ollama三、OpenWebUI + Phi3Ollama+OpenWebUI+Phi3本地大模型入门 完全不懂大模型的请绕道,相信我李一舟的课程比较适合 Ollama提供大模型运行环境,OpenWebUI提供UI,Phi3就是那个大模型。 当然,Ollama支持超级…...
实战15:bert 命名实体识别、地址解析、人名电话地址抽取系统-完整代码数据
直接看项目视频演示: bert 命名实体识别、关系抽取、人物抽取、地址解析、人名电话地址提取系统-完整代码数据_哔哩哔哩_bilibili 项目演示: 代码: import re from transformers import BertTokenizer, BertForTokenClassification, pipeline import os import torch im…...

js 表格添加|删除一行交互
一、需求 二、实现 <div style"margin-bottom: 55px"><form action"" method"post" enctype"multipart/form-data" id"reportForm" name"sjf" style"margin-left: 25px;margin-bottom: 50px;&quo…...

如何选择合适的服务器硬件和配置?
业务需求 了解您的业务需求和负载。这将帮助您确定需要哪种类型的服务器(如文件服务器、数据库服务器、Web服务器等)以及所需的处理能力、内存、存储和网络性能。...
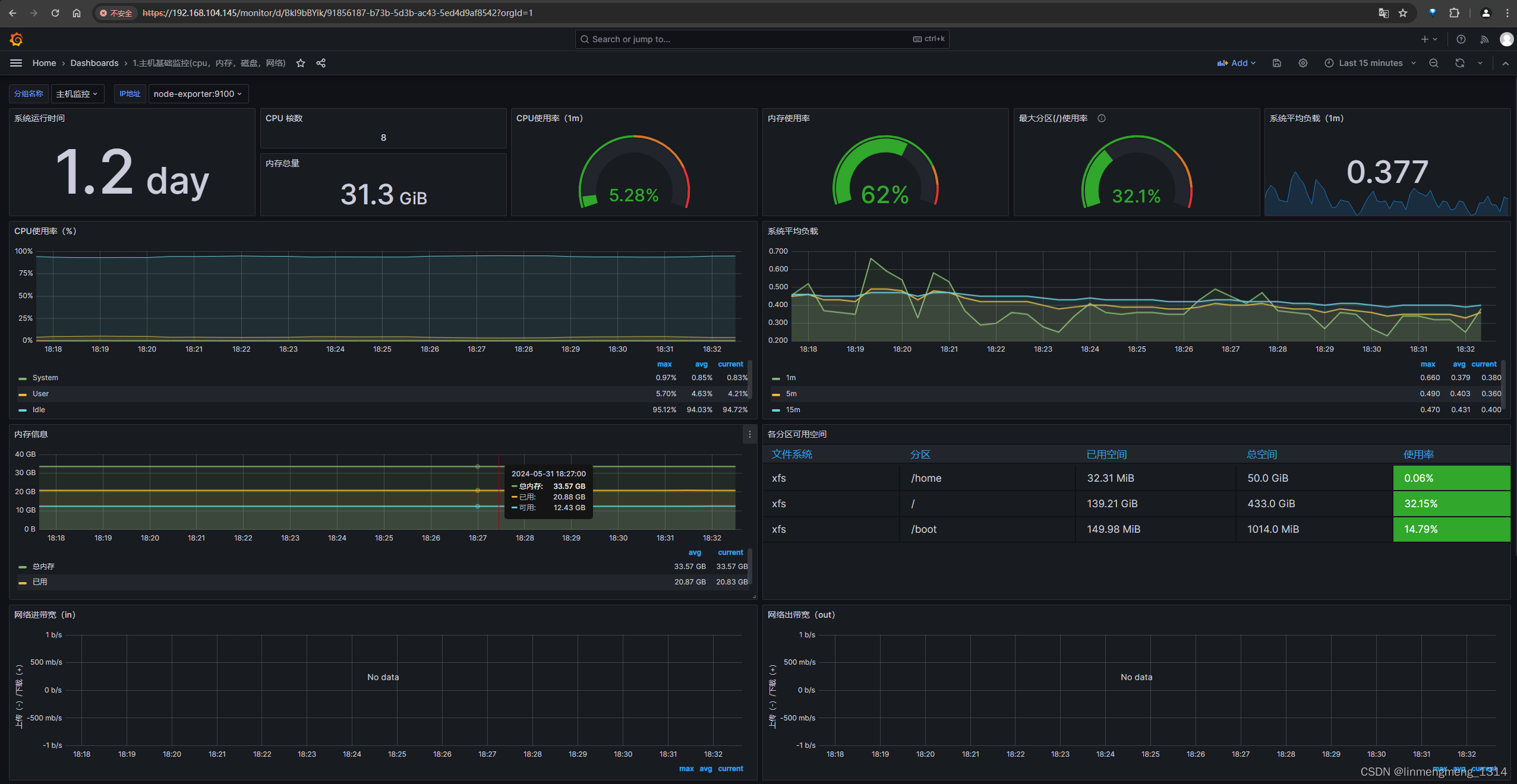
Prometheus + Grafana + Alertmanager 系统监控
PrometheusGrafana 系统监控 1. 简介1.1 Prometheus 普罗 米修斯1.2 Grafana 2. 快速试用2.1 Prometheus 普罗 米修斯2.2 Prometheus 配置文件2.3 Grafana 2. 使用 Docker-Compose脚本部署监控服务3. Grafana 配置3.1 配置数据源 Prometheus3.2 使用模板ID 配置监控模板3.3 使用…...

5.23R语言-参数假设检验
理论 方差分析(ANOVA, Analysis of Variance)是统计学中用来比较多个样本均值之间差异的一种方法。它通过将总变异分解为不同来源的变异来检测因子对响应变量的影响。方差分析广泛应用于实验设计、质量控制、医学研究等领域。 方差分析的基本模型 方差…...

rnn 和lstm源码学习笔记
目录 rnn学习笔记 lstm学习笔记 rnn学习笔记 import torchdef rnn(inputs, state, params):# inputs的形状: (时间步数量, 批次大小, 词表大小)W_xh, W_hh, b_h, W_hq, b_q paramsH stateoutputs []# 遍历每个时间步for X in inputs:# 计算隐藏状态 HH torch.tanh(torch.…...

解析Java中1000个常用类:CharSequence类,你学会了吗?
在 Java 编程中,字符串操作是最常见的任务之一。为了提供一种灵活且统一的方式来处理不同类型的字符序列,Java 引入了 CharSequence 接口。 通过实现 CharSequence 接口,各种字符序列类可以提供一致的 API,增强了代码的灵活性和可扩展性。 本文将深入探讨 CharSequence 接…...

微服务远程调用之拦截器实战
微服务远程调用之拦截器实战 前言: 在我们开发过程中,很可能是项目是从0到1开发,或者在原有基础上做二次开发,这次是根据已有代码做二次开发,需要在我们微服务一【这里方便举例,我们后面叫模版微服务】调用…...

德人合科技——天锐绿盾内网安全管理软件 | -文档透明加密模块
天锐绿盾文档加密功能能够为各种模式的电子文档提供高强度加密保护,丰富的权限控制以及灵活的应用管理,帮助企业构建更严密的立体保密体系。 PC地址: https://isite.baidu.com/site/wjz012xr/2eae091d-1b97-4276-90bc-6757c5dfedee ————…...
超融合架构下,虚拟机高可用机制如何构建?
作者:SmartX 产品部 钟锦锌 虚拟机高可用(High Availability,简称 HA)是虚拟化/超融合平台最常用、关键的功能之一,可在服务器发生故障时通过重建业务虚拟机以降低故障对业务带来的影响。因此,为了充分保障…...
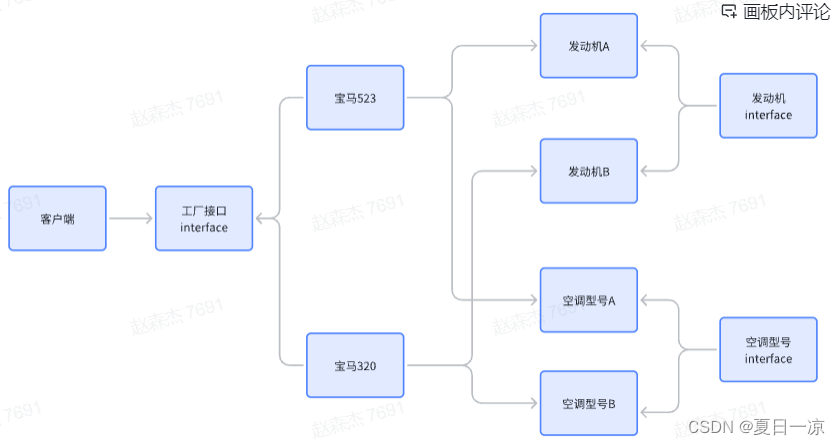
工厂模式详情
一.介绍工厂模式的用途与特点 工厂方法模式是一种创建型设计模式, 其在父类中提供一个创建对象的方法, 允许子类决定实例化对象的类型。定义工厂方法模式(Fatory Method Pattern)是指定义一个创建对象的接口,但让实现这个接口的类来决定实例…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
