平衡二叉树的应用举例
AVL 是一种自平衡二叉搜索树,其中任何节点的左右子树的高度之差不能超过 1。
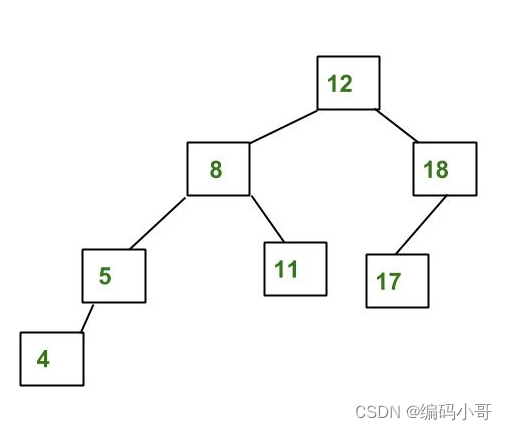
AVL树的特点:
1、它遵循二叉搜索树的一般属性。
2、树的每个子树都是平衡的,即左右子树的高度之差最多为1。
3、当插入新节点时,树会自我平衡。因此,插入操作非常耗时。
AVL Tree的应用:
1、大多数内存中集和字典都使用 AVL 树进行存储。
2、数据库应用程序(插入和删除不太常见,但需要频繁的数据查找)也经常使用 AVL 树。
3、除了数据库应用程序之外,它还用于其他需要更好搜索的应用程序。
4、有序关联容器(集合、多集、映射和多映射)的大多数 STL 实现都使用红黑树而不是 AVL树。
#include <stdio.h>
#include <stdlib.h>struct AVLnode
{int key;struct AVLnode *left;struct AVLnode *right;int height;
};
typedef struct AVLnode avlNode;int max(int a, int b) { return (a > b) ? a : b; }avlNode *newNode(int key)
{avlNode *node = (avlNode *)malloc(sizeof(avlNode));if (node == NULL)printf("!! Out of Space !!\n");else{node->key = key;node->left = NULL;node->right = NULL;node->height = 0;}return node;
}int nodeHeight(avlNode *node)
{if (node == NULL)return -1;elsereturn (node->height);
}int heightDiff(avlNode *node)
{if (node == NULL)return 0;elsereturn (nodeHeight(node->left) - nodeHeight(node->right));
}/* 返回左子树中最小值的节点*/
avlNode *minNode(avlNode *node)
{avlNode *temp = node;while (temp->left != NULL) temp = temp->left;return temp;
}void printAVL(avlNode *node, int level)
{int i;if (node != NULL){printAVL(node->right, level + 1);printf("\n\n");for (i = 0; i < level; i++) printf("\t");printf("%d", node->key);printAVL(node->left, level + 1);}
}avlNode *rightRotate(avlNode *z)
{avlNode *y = z->left;avlNode *T3 = y->right;y->right = z;z->left = T3;z->height = (max(nodeHeight(z->left), nodeHeight(z->right)) + 1);y->height = (max(nodeHeight(y->left), nodeHeight(y->right)) + 1);return y;
}avlNode *leftRotate(avlNode *z)
{avlNode *y = z->right;avlNode *T3 = y->left;y->left = z;z->right = T3;z->height = (max(nodeHeight(z->left), nodeHeight(z->right)) + 1);y->height = (max(nodeHeight(y->left), nodeHeight(y->right)) + 1);return y;
}avlNode *LeftRightRotate(avlNode *z)
{z->left = leftRotate(z->left);return (rightRotate(z));
}avlNode *RightLeftRotate(avlNode *z)
{z->right = rightRotate(z->right);return (leftRotate(z));
}avlNode *insert(avlNode *node, int key)
{if (node == NULL)return (newNode(key));/*二叉搜索树插入*/if (key < node->key)node->left =insert(node->left, key); /*递归插入左子树*/else if (key > node->key)node->right =insert(node->right, key); /*递归插入右子树*//*计算节点高度*/node->height = (max(nodeHeight(node->left), nodeHeight(node->right)) + 1);/*检查平衡性*/int balance = heightDiff(node);/*左左*/if (balance > 1 && key < (node->left->key))return rightRotate(node);/*右右*/if (balance < -1 && key > (node->right->key))return leftRotate(node);/*左右*/if (balance > 1 && key > (node->left->key)){node = LeftRightRotate(node);}/*右左*/if (balance < -1 && key < (node->right->key)){node = RightLeftRotate(node);}return node;
}avlNode *delete (avlNode *node, int queryNum)
{if (node == NULL)return node;if (queryNum < node->key)node->left =delete (node->left, queryNum); /*Recursive deletion in L subtree*/else if (queryNum > node->key)node->right =delete (node->right, queryNum); /*Recursive deletion in R subtree*/else{/*单节点或者没有子节点*/if ((node->left == NULL) || (node->right == NULL)){avlNode *temp = node->left ? node->left : node->right;/*没有子节点*/if (temp == NULL){temp = node;node = NULL;}else /*单节点*/*node = *temp;free(temp);}else{/*两个孩子节点*//*获取右子树最小值的节点*/avlNode *temp = minNode(node->right);node->key = temp->key; /*拷贝到根节点*/node->right =delete (node->right,temp->key); /*删除右子树最小值的节点*/}}/*单节点*/if (node == NULL)return node;/*更新高度*/node->height = (max(nodeHeight(node->left), nodeHeight(node->right)) + 1);int balance = heightDiff(node);/*左左*/if ((balance > 1) && (heightDiff(node->left) >= 0))return rightRotate(node);/*左右*/if ((balance > 1) && (heightDiff(node->left) < 0)){node = LeftRightRotate(node);}/*右右*/if ((balance < -1) && (heightDiff(node->right) >= 0))return leftRotate(node);/*右左*/if ((balance < -1) && (heightDiff(node->right) < 0)){node = RightLeftRotate(node);}return node;
}avlNode *findNode(avlNode *node, int queryNum)
{if (node != NULL){if (queryNum < node->key)node = findNode(node->left, queryNum);else if (queryNum > node->key)node = findNode(node->right, queryNum);}return node;
}void printPreOrder(avlNode *node)
{if (node == NULL)return;printf(" %d ", (node->key));printPreOrder(node->left);printPreOrder(node->right);
}void printInOrder(avlNode *node)
{if (node == NULL)return;printInOrder(node->left);printf(" %d ", (node->key));printInOrder(node->right);
}void printPostOrder(avlNode *node)
{if (node == NULL)return;printPostOrder(node->left);printPostOrder(node->right);printf(" %d ", (node->key));
}int main()
{int choice;int flag = 1;int insertNum;int queryNum;avlNode *root = NULL;avlNode *tempNode;while (flag == 1){printf("\n\nEnter the Step to Run : \n");printf("\t1: Insert a node into AVL tree\n");printf("\t2: Delete a node in AVL tree\n");printf("\t3: Search a node into AVL tree\n");printf("\t4: printPreOrder (Ro L R) Tree\n");printf("\t5: printInOrder (L Ro R) Tree\n");printf("\t6: printPostOrder (L R Ro) Tree\n");printf("\t7: printAVL Tree\n");printf("\t0: EXIT\n");scanf("%d", &choice);switch (choice){case 0:{flag = 0;printf("\n\t\tExiting, Thank You !!\n");break;}case 1:{printf("\n\tEnter the Number to insert: ");scanf("%d", &insertNum);tempNode = findNode(root, insertNum);if (tempNode != NULL)printf("\n\t %d Already exists in the tree\n", insertNum);else{printf("\n\tPrinting AVL Tree\n");printAVL(root, 1);printf("\n");root = insert(root, insertNum);printf("\n\tPrinting AVL Tree\n");printAVL(root, 1);printf("\n");}break;}case 2:{printf("\n\tEnter the Number to Delete: ");scanf("%d", &queryNum);tempNode = findNode(root, queryNum);if (tempNode == NULL)printf("\n\t %d Does not exist in the tree\n", queryNum);else{printf("\n\tPrinting AVL Tree\n");printAVL(root, 1);printf("\n");root = delete (root, queryNum);printf("\n\tPrinting AVL Tree\n");printAVL(root, 1);printf("\n");}break;}case 3:{printf("\n\tEnter the Number to Search: ");scanf("%d", &queryNum);tempNode = findNode(root, queryNum);if (tempNode == NULL)printf("\n\t %d : Not Found\n", queryNum);else{printf("\n\t %d : Found at height %d \n", queryNum,tempNode->height);printf("\n\tPrinting AVL Tree\n");printAVL(root, 1);printf("\n");}break;}case 4:{printf("\nPrinting Tree preOrder\n");printPreOrder(root);break;}case 5:{printf("\nPrinting Tree inOrder\n");printInOrder(root);break;}case 6:{printf("\nPrinting Tree PostOrder\n");printPostOrder(root);break;}case 7:{printf("\nPrinting AVL Tree\n");printAVL(root, 1);break;}default:{flag = 0;printf("\n\t\tExiting, Thank You !!\n");break;}}}return 0;
}
相关文章:

平衡二叉树的应用举例
AVL 是一种自平衡二叉搜索树,其中任何节点的左右子树的高度之差不能超过 1。 AVL树的特点: 1、它遵循二叉搜索树的一般属性。 2、树的每个子树都是平衡的,即左右子树的高度之差最多为1。 3、当插入新节点时,树会自我平衡。因此…...
一键安装 HaloDB 之 Ansible for Halo
↑ 关注“少安事务所”公众号,欢迎⭐收藏,不错过精彩内容~ 前倾回顾 前面介绍了“光环”数据库的基本情况和安装办法。 哈喽,国产数据库!Halo DB! 三步走,Halo DB 安装指引 以及 HaloDB 的 Oracle 和 MySQL 兼容模式: …...

el-table的上下筛选功能
el-table的sort-change事件可以监听到筛选的事件; 会返回prop属性和order排序的顺序; html: <el-table :data"tableData" border style"width: 100%" :cell-style"{ textAlign: center }"header-cell-c…...
)
【手撕面试题】Vue(高频知识点一)
每天10道题,100天后,搞定所有前端面试的高频知识点,加油!!!,在看文章的同时,希望不要直接看答案,先思考一下自己会不会,如果会,自己的答案是什么&…...

LabVIEW车轮动平衡检测系统
LabVIEW车轮动平衡检测系统 随着汽车行业的快速发展,车轮动平衡问题对乘坐舒适性、操控稳定性及安全性的影响日益凸显,成为了提高汽车性能的一个关键环节。传统的检测系统因精度低、成本高、操作复杂等问题,难以满足现代汽车行业的需求。开发…...

【Python爬虫--scrapy+selenium框架】超详细的Python爬虫scrapy+selenium框架学习笔记(保姆级别的,非常详细)
六,selenium 想要下载PDF或者md格式的笔记请点击以下链接获取 python爬虫学习笔记点击我获取 Scrapyselenium详细学习笔记点我获取 Python超详细的学习笔记共21万字点我获取 1,下载配置 ## 安装: pip install selenium## 它与其他库不同…...
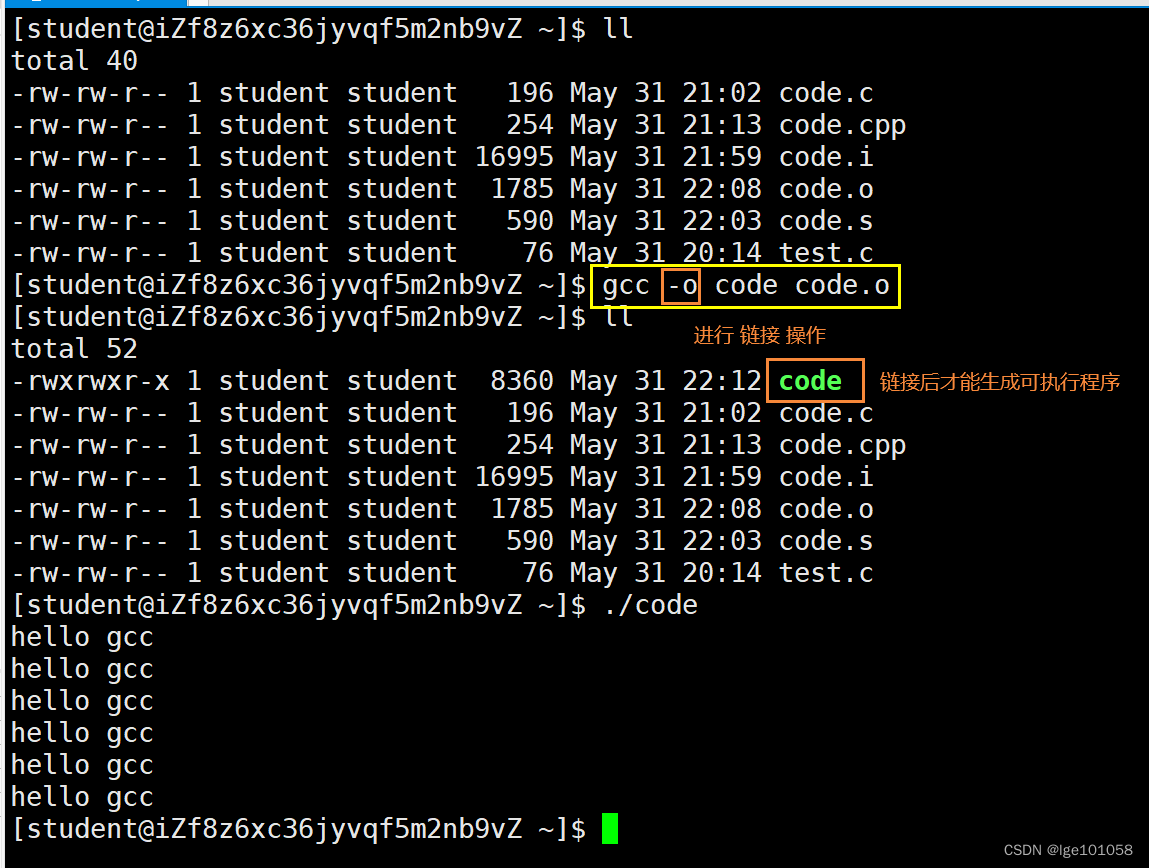
【Linux】Linux环境基础开发工具_3
文章目录 四、Linux环境基础开发工具2. vim3. gcc和g动静态库的理解 未完待续 四、Linux环境基础开发工具 2. vim vim 怎么批量化注释呢?最简单的方法就是在注释开头和结尾输入 /* 或 */ 。当然也可以使用快捷键: Ctrl v 按 hjkl 光标移动进行区域选择…...

数字水印 | 图像噪声攻击(高斯/椒盐/泊松/斑点)
目录 Noise Attack1 高斯噪声(Gaussian Noise)2 椒盐噪声(Salt and Pepper Noise)3 泊松噪声(Poisson Noise)4 斑点噪声(Speckle Noise)5 完整代码 参考博客:Python…...
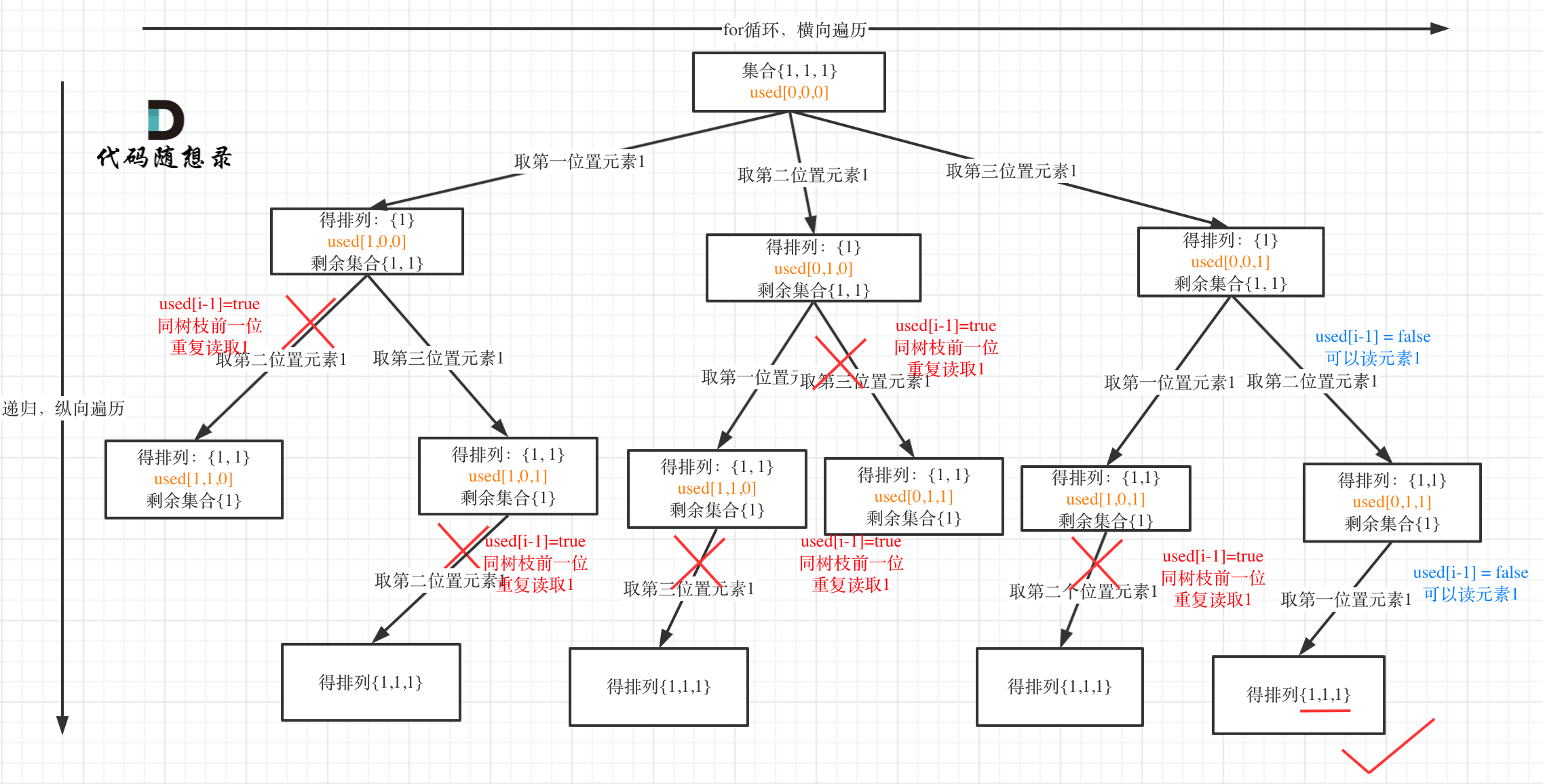
LeetCode-47 全排列Ⅱ
LeetCode-47 全排列Ⅱ 题目描述解题思路代码说明 题目描述 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 : 输入:nums [1,1,2]输出: [[1,1,2], [1,2,1], [2,1,1]] b站题目解读讲的不好&…...
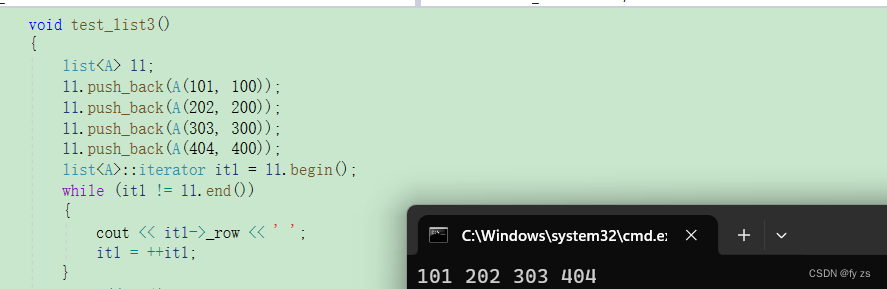
list 的实现
目录 list 结点类 结点类的构造函数 list的尾插尾删 list的头插头删 迭代器 运算符重载 --运算符重载 和! 运算符重载 * 和 -> 运算符重载 list 的insert list的erase list list实际上是一个带头双向循环链表,要实现list,则首先需要实现一个结点类,而一个结点需要…...
学法)
一个程序员的牢狱生涯(47)学法
星期一 学法 二铺不知道什么时候走到了我的身边,向我说道,这是二铺在我进来号子后主动过来和我说话。 我听到二铺这声突兀的说话后,抬起头。这时我才看到,除了二铺,还有六子、棍子都围在我的身边,看着我。虽然六子和棍子依旧一副‘吊儿郎当’的样子,但我从他们几个的眼神…...
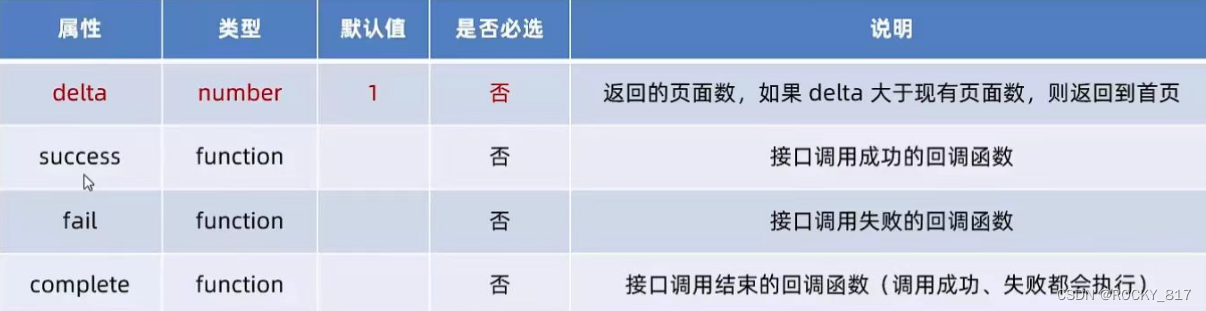
微信小程序-页面导航
一、页面导航 页面导航指的是页面之间的相互跳转,例如:浏览器中实现页面导航的方式有如下两种: 1.<a>链接 2.location.href 二、小程序中实现页面导航的两种方式 1.声明式导航 在页面上声明一个<navigator>导航组件 通过点击…...
 服务质量(Quality of Service, QoS))
计算机网络- 特定服务类型(Type of Service, TOS) 服务质量(Quality of Service, QoS)
特定服务类型(Type of Service, TOS) 具有特定服务类型(Type of Service, TOS)的数据包是指在IP头部中包含特定TOS字段设置的数据包。TOS字段用于指示数据包的服务质量要求,如延迟、吞吐量、可靠性等。现代IP网络通常…...
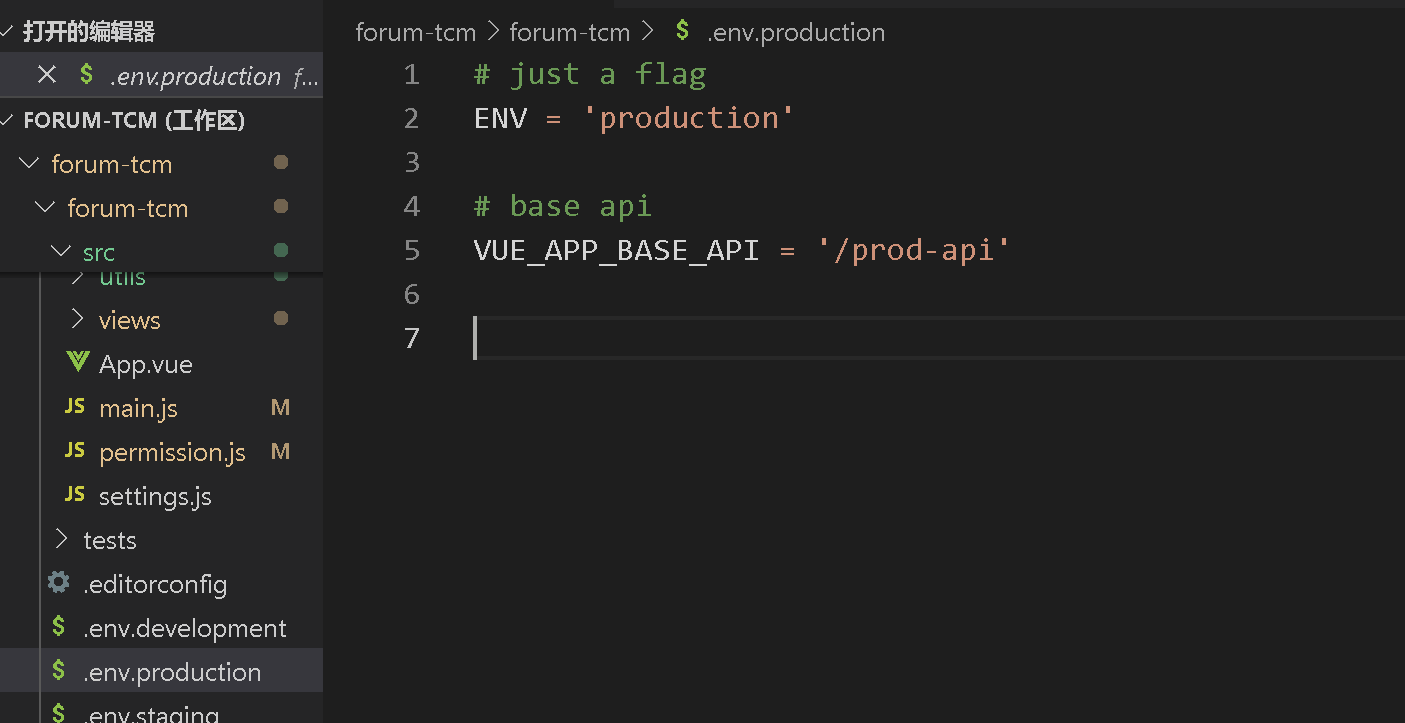
2.6 Docker部署多个前端项目
2.6 Docker部署多个项目 三. 部署前端项目 1.将前端项目打包到同一目录下(tcm-ui) 2. 部署nginx容器 docker run --namenginx -p 9090:9090 -p 9091:9091 -d nginx3. 复制nginx.conf文件到主机目录 docker cp nginx:/etc/nginx/nginx.conf /root/ja…...
如何格式化只读U盘?
U盘只读无法格式化,该怎么处理?别担心!本文将向你提供一些实用方法,助你解决U盘写保护的难题。这些方法能有效帮助你解除U盘的只读状态,从而可以顺利进行格式化和其他操作。 不能格式化只读U盘 “我购买了一个U盘&…...

【并查集】专题练习
题目列表 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 模板 836. 合并集合 - AcWing题库 #include<bits/stdc.h> using lllong long; //#define int ll const int N1e510,mod1e97; int n,m; int p[N],sz[N]; int find(int a) {if(p[a]!a) p[a]find(p[a]);return p[a…...
服装连锁店收银系统需要具备的五大功能
当今服装连锁店在市场竞争中需要拥有高效的收银系统来提升业务效率和顾客满意度。以下是服装连锁店收银系统需要具备的五大功能: 首先,完善的商品管理功能是至关重要的。这包括商品信息的录入、管理、更新和查询。收银系统应该能够快速而准确地识别商品&…...
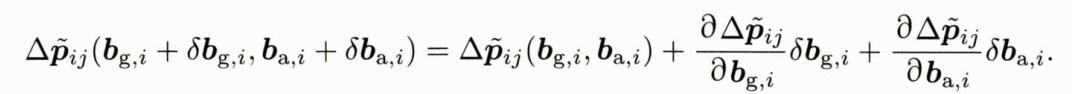
IMU状态预积分代码实现 —— IMU状态预积分类
IMU状态预积分代码实现 —— IMU状态预积分类 实现IMU状态预积分类 实现IMU状态预积分类 首先,实现预积分自身的结构。一个预积分类应该存储一下数据: 预积分的观测量 △ R ~ i j , △ v ~ i j , △ p ~ i j \bigtriangleup \tilde{R} _{ij},\bigtrian…...

C语言编程:探索最小公倍数的奥秘
C语言编程:探索最小公倍数的奥秘 在编程的世界中,计算两个数的最小公倍数(LCM)是一个常见的数学问题。C语言作为一种基础且强大的编程语言,为我们提供了实现这一功能的工具。本文将从四个方面、五个方面、六个方面和七…...
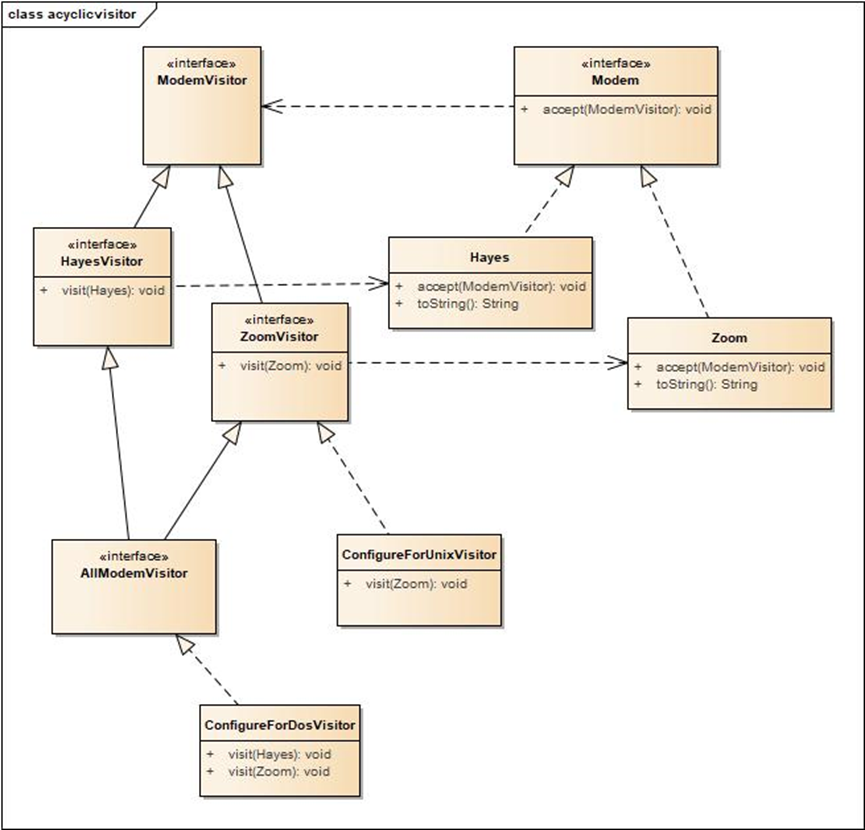
Java设计模式-活动对象与访问者
活动对象 Java设计模式中,活动对象是指一个对象始终处于活动的状态,该对象包括一个线程安全的数据结构以及一个活跃的执行线程。 如上所示,ActiveCreature类的构造函数初始化一个线程安全的数据结构(阻塞队列)、初始化…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
