模糊C均值(FCM)算法更新公式推导
模糊C均值(FCM)算法更新公式推导
目标函数
FCM的目标函数为:
J m = ∑ i = 1 n ∑ j = 1 k u i j m ∥ x i − c j ∥ 2 J_m = \sum_{i=1}^n \sum_{j=1}^k u_{ij}^m \|x_i - c_j\|^2 Jm=i=1∑nj=1∑kuijm∥xi−cj∥2
其中:
- x i x_i xi 是数据点, i = 1 , 2 , … , n i = 1, 2, \ldots, n i=1,2,…,n。
- c j c_j cj 是第 j j j 个簇的中心, j = 1 , 2 , … , k j = 1, 2, \ldots, k j=1,2,…,k。
- u i j u_{ij} uij 是数据点 x i x_i xi 属于第 j j j 个簇的隶属度。
- m m m 是模糊度参数,通常 m > 1 m > 1 m>1。
更新公式推导过程
1. 定义目标函数
J m = ∑ i = 1 n ∑ j = 1 k u i j m ∥ x i − c j ∥ 2 J_m = \sum_{i=1}^n \sum_{j=1}^k u_{ij}^m \|x_i - c_j\|^2 Jm=i=1∑nj=1∑kuijm∥xi−cj∥2
2. 引入约束条件
∑ j = 1 k u i j = 1 ∀ i \sum_{j=1}^k u_{ij} = 1 \quad \forall i j=1∑kuij=1∀i
使用拉格朗日乘数法,引入拉格朗日乘子 λ i \lambda_i λi,构造拉格朗日函数:
L = ∑ i = 1 n ∑ j = 1 k u i j m ∥ x i − c j ∥ 2 + ∑ i = 1 n λ i ( ∑ j = 1 k u i j − 1 ) \mathcal{L} = \sum_{i=1}^n \sum_{j=1}^k u_{ij}^m \|x_i - c_j\|^2 + \sum_{i=1}^n \lambda_i \left( \sum_{j=1}^k u_{ij} - 1 \right) L=i=1∑nj=1∑kuijm∥xi−cj∥2+i=1∑nλi(j=1∑kuij−1)
3. 对 u i j u_{ij} uij 求偏导数并设为零
对拉格朗日函数 L \mathcal{L} L 求 u i j u_{ij} uij 的偏导数并设为零:
∂ L ∂ u i j = m u i j m − 1 ∥ x i − c j ∥ 2 + λ i = 0 \frac{\partial \mathcal{L}}{\partial u_{ij}} = m u_{ij}^{m-1} \|x_i - c_j\|^2 + \lambda_i = 0 ∂uij∂L=muijm−1∥xi−cj∥2+λi=0
解这个方程得到:
u i j m − 1 = − λ i m ∥ x i − c j ∥ 2 u_{ij}^{m-1} = -\frac{\lambda_i}{m \|x_i - c_j\|^2} uijm−1=−m∥xi−cj∥2λi
为了保证 (u_{ij}) 非负,设 λ i = − m ζ \lambda_i = -m\zeta λi=−mζ,则:
u i j m − 1 = ζ ∥ x i − c j ∥ 2 u_{ij}^{m-1} = \frac{\zeta}{\|x_i - c_j\|^2} uijm−1=∥xi−cj∥2ζ
即:
u i j = ( ζ ∥ x i − c j ∥ 2 ) 1 m − 1 u_{ij} = \left( \frac{\zeta}{\|x_i - c_j\|^2} \right)^{\frac{1}{m-1}} uij=(∥xi−cj∥2ζ)m−11
4. 求解拉格朗日乘子 ζ \zeta ζ
利用约束条件 ∑ j = 1 k u i j = 1 \sum_{j=1}^k u_{ij} = 1 ∑j=1kuij=1:
∑ j = 1 k ( ζ ∥ x i − c j ∥ 2 ) 1 m − 1 = 1 \sum_{j=1}^k \left( \frac{\zeta}{\|x_i - c_j\|^2} \right)^{\frac{1}{m-1}} = 1 j=1∑k(∥xi−cj∥2ζ)m−11=1
解这个方程得到:
ζ = ( ∑ j = 1 k ( 1 ∥ x i − c j ∥ 2 ) 1 m − 1 ) 1 − m \zeta = \left( \sum_{j=1}^k \left( \frac{1}{\|x_i - c_j\|^2} \right)^{\frac{1}{m-1}} \right)^{1-m} ζ=(j=1∑k(∥xi−cj∥21)m−11)1−m
代入 u i j u_{ij} uij 的表达式,得到隶属度更新公式:
u i j = 1 ∑ l = 1 k ( ∥ x i − c j ∥ ∥ x i − c l ∥ ) 2 m − 1 u_{ij} = \frac{1}{\sum_{l=1}^k \left( \frac{\|x_i - c_j\|}{\|x_i - c_l\|} \right)^{\frac{2}{m-1}}} uij=∑l=1k(∥xi−cl∥∥xi−cj∥)m−121
5. 对簇中心 c j c_j cj 求偏导数并设为零
对目标函数 J m J_m Jm 对 c j c_j cj 求偏导数并设为零:
∂ J m ∂ c j = ∑ i = 1 n u i j m ( c j − x i ) = 0 \frac{\partial J_m}{\partial c_j} = \sum_{i=1}^n u_{ij}^m (c_j - x_i) = 0 ∂cj∂Jm=i=1∑nuijm(cj−xi)=0
解这个方程得到:
∑ i = 1 n u i j m c j = ∑ i = 1 n u i j m x i \sum_{i=1}^n u_{ij}^m c_j = \sum_{i=1}^n u_{ij}^m x_i i=1∑nuijmcj=i=1∑nuijmxi
c j = ∑ i = 1 n u i j m x i ∑ i = 1 n u i j m c_j = \frac{\sum_{i=1}^n u_{ij}^m x_i}{\sum_{i=1}^n u_{ij}^m} cj=∑i=1nuijm∑i=1nuijmxi
总结
通过上述推导过程,我们得到了FCM算法的更新公式:
- 隶属度更新公式:
u i j = 1 ∑ l = 1 k ( ∥ x i − c j ∥ ∥ x i − c l ∥ ) 2 m − 1 u_{ij} = \frac{1}{\sum_{l=1}^k \left(\frac{\|x_i - c_j\|}{\|x_i - c_l\|}\right)^{\frac{2}{m-1}}} uij=∑l=1k(∥xi−cl∥∥xi−cj∥)m−121
- 簇中心更新公式:
c j = ∑ i = 1 n u i j m x i ∑ i = 1 n u i j m c_j = \frac{\sum_{i=1}^n u_{ij}^m x_i}{\sum_{i=1}^n u_{ij}^m} cj=∑i=1nuijm∑i=1nuijmxi
这些公式在每次迭代中交替更新,直到目标函数收敛。
相关文章:
算法更新公式推导)
模糊C均值(FCM)算法更新公式推导
模糊C均值(FCM)算法更新公式推导 目标函数 FCM的目标函数为: J m ∑ i 1 n ∑ j 1 k u i j m ∥ x i − c j ∥ 2 J_m \sum_{i1}^n \sum_{j1}^k u_{ij}^m \|x_i - c_j\|^2 Jmi1∑nj1∑kuijm∥xi−cj∥2 其中: …...

金融创新浪潮下的拆分盘投资探索
随着数字化时代的步伐加速,金融领域正经历着前所未有的变革。在众多金融创新中,拆分盘作为一种新兴的投资模式,以其独特的增长机制,吸引了投资者的广泛关注。本文将对拆分盘的投资逻辑进行深入剖析,并结合具体案例&…...

一份不知道哪里来的第十五届国赛模拟题
这是一个不知道来源的模拟题目,没有完全完成,只作代码记录,不作分析和展示,极其冗长,但里面有长按短按双击的复合,可以看看。 目录 题目代码底层驱动主程序核心代码关键:双击单击长按复合代码 …...
机器人动力学模型与MATLAB仿真
机器人刚体动力学由以下方程控制!!! startup_rvc mdl_puma560 p560.dyn 提前计算出来这些“disturbance”,然后在控制环路中将它“抵消”(有时候也叫前馈控制) 求出所需要的力矩,其中M项代表克服…...
SAPUI5基础知识3 - 引导过程(Bootstrap)
1. 背景 在上一篇博客中,我们已经建立出了第一个SAPUI5项目,接下来,我们将为这个项目添加引导过程。 在动手练习之前,让我们先解释一下什么引导过程。 1.1 什么是引导过程? 在计算机科学中,引导过程也称…...

ABAP 借助公司封装的钉钉URL,封装的RFC给钉钉发送消息
FUNCTION ZRFC_BC_SMSSEND_DINGTALK. *"---------------------------------------------------------------------- *"*"本地接口: *" IMPORTING *" VALUE(DESTUSRID) TYPE CHAR255 *" VALUE(CONTENT) TYPE CHAR255 *&quo…...

登录校验及全局异常处理器
登录校验 会话技术 会话:用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束.在一次会话中可以包含多次请求和响应会话跟踪:一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一浏览器,以便在同一次会话请求间共享数据会话跟踪方案 客户端…...
计算机视觉与模式识别实验1-2 图像的形态学操作
文章目录 🧡🧡实验流程🧡🧡1.图像膨胀2.图像腐蚀3.膨胀与腐蚀的综合使用4.对下面二值图像的目标提取骨架,并分析骨架结构。 🧡🧡全部代码🧡🧡 🧡🧡…...

【前端每日基础】day31——uni-app
uni-app 开发详细介绍 基本概念 uni-app:uni-app 是一个使用 Vue.js 开发多端应用的框架,可以编译到微信小程序、支付宝小程序、百度小程序、字节跳动小程序、H5、App等多个平台。 跨平台:一次开发,多端部署。通过条件编译实现多…...

云动态摘要 2024-05-31
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [1.5折起]年中盛惠--AI分会场 腾讯云 2024-05-30 人脸核身、语音识别、文字识别、数智人、腾讯混元等热门AI产品特惠,1.5折起 云服务器ECS试用产品续用 阿里云 2024-04-14 云…...

Oracle数据块如何存储真实数据
上周休假了几天,颓废了,没有输出。今天写一点内容。 先抛出一个问题。表中的数据在Oracle数据块中是如何存储的呢?今天简单说一下这个问题。通常数据库中的表会存储字符,数字,日期 这3种常见的数据类型。下面的例子就用这3种数据类型作说明 首先,Oracle数据块底层存储这…...

【WEB前端2024】开源智体世界:乔布斯3D纪念馆-第30课-门的移动动画
【WEB前端2024】开源智体世界:乔布斯3D纪念馆-第30课-门的移动动画 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。dtns.network是一款主要由JavaScript编写的智体世界引擎…...

智能化改造给企业带来的实际效果
1. 提高生产效率:通过自动化和智能化的生产线,减少人工操作,显著提升单位时间内的生产量。 2. 提升产品质量:智能化改造通过精确控制生产过程,减少人为错误,提高产品的一致性和可靠性。 3. 降低生产成本&am…...

深度学习-语言模型
深度学习-语言模型 统计语言模型神经网络语言模型语言模型的应用序列模型(Sequence Model)语言模型(Language Model)序列模型和语言模型的区别 语言模型(Language Model)是自然语言处理(NLP&…...

微型导轨在自动化制造中有哪些优势?
微型导轨在自动化制造中发挥重要作用,能够满足自动化设备制造中对精度要求较高的工艺环节。适用于自动装配线、自动检测设备和机器人操作等环节,推动了行业的进步与发展。那么,微型导轨在使用中有哪些优势呢? 1、精度高和稳定性强…...

探索气象数据的多维度三维可视化:PM2.5、风速与高度分析
探索气象数据的多维度可视化:PM2.5、风速与高度分析 摘要 在现代气象学中,数据可视化是理解复杂气象模式和趋势的关键工具。本文将介绍一种先进的数据可视化技术,它能够将PM2.5浓度、风速和高度等多维度数据以直观和动态的方式展现出来。 …...

【传知代码】双深度学习模型实现结直肠癌检测(论文复现)
前言:在医学领域,科技的进步一直是改变人类生活的关键驱动力之一。随着深度学习技术的不断发展,其在医学影像诊断领域的应用正日益受到关注。结直肠癌是一种常见但危害极大的恶性肿瘤,在早期发现和及时治疗方面具有重要意义。然而…...
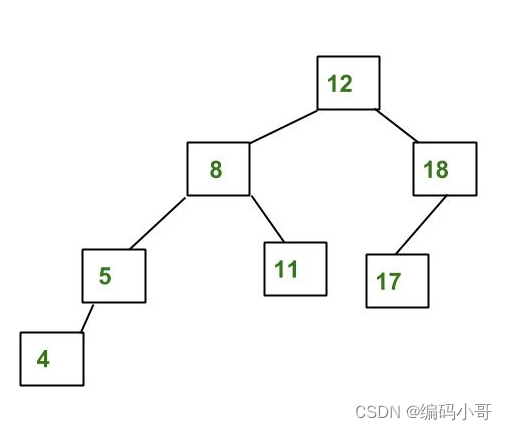
平衡二叉树的应用举例
AVL 是一种自平衡二叉搜索树,其中任何节点的左右子树的高度之差不能超过 1。 AVL树的特点: 1、它遵循二叉搜索树的一般属性。 2、树的每个子树都是平衡的,即左右子树的高度之差最多为1。 3、当插入新节点时,树会自我平衡。因此…...
一键安装 HaloDB 之 Ansible for Halo
↑ 关注“少安事务所”公众号,欢迎⭐收藏,不错过精彩内容~ 前倾回顾 前面介绍了“光环”数据库的基本情况和安装办法。 哈喽,国产数据库!Halo DB! 三步走,Halo DB 安装指引 以及 HaloDB 的 Oracle 和 MySQL 兼容模式: …...

el-table的上下筛选功能
el-table的sort-change事件可以监听到筛选的事件; 会返回prop属性和order排序的顺序; html: <el-table :data"tableData" border style"width: 100%" :cell-style"{ textAlign: center }"header-cell-c…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
